基于三相Biot速度應力波動方程的水合物儲層波場數值模擬

石仁剛 魏周拓 葛新民 鄧少貴 祁磊 姚志廣

摘要：天然氣水合物儲層可以看作由骨架、水合物和孔隙水構成的三相孔隙介質。以三相Biot一階速度應力波動方程作為聲波在水合物儲層傳播的控制方程，用有限差分法（FDTD）進行數值模擬。波場快照可以清楚展現3個縱波和兩個橫波，與Biot理論相符。根據實測速度優化控制方程參數，使數值速度與實測速度相符。結果表明：孔隙度對水合物剪應力分量影響最顯著，對水合物、孔隙水和骨架速度分量的影響次之，所以儲層中孔隙度最適合用水合物剪應力分量來分析。骨架速度分量和應力分量受飽和度的影響較小，水合物剪應力分量受飽和度的影響最大，所以分析儲層中水合物飽和度的最佳選擇是水合物剪應力分量。

關鍵詞：水合物儲層可視化； 三相Biot波動方程； 有限差分法;孔隙度； 水合物飽和度； 完全匹配層

中圖分類號：P 631.4?? 文獻標志碼：A

文章編號：1673-5005（2024）03-0057-08?? doi：10.3969/j.issn.1673-5005.2024.03.006

Numerical simulation of hydrate reservoir based on three-phase Biot velocity-stress wave equaiton

SHI Rengang1，2， WEI Zhoutuo2，3， GE Xinmin2，3， DENG Shaogui2，3， QI Lei4， YAO Zhiguang4

（1.School of Science in China University of Petroleum（East China）， Qingdao 266580， China;2.State Key Laboratory of Deep Oil and Gas， China University of Petroleum（East China）， Qingdao 266580， China;3.School of Geosciences in China University of Petroleum（East China）， Qingdao 266580， China;4.CPOE Research Institute of Engineering Technology， Tianjin 300451， China）

Abstract：Natural gas hydrate reservoirs are considered as three-phase porous media， comprising skeleton， hydrate， and pore water. Utilizing the three-phase Biot first-order velocity stress wave equation as the governing equation for sound wave propagation in gas hydrate reservoirs， numerical simulations are conducted employing the finite difference time domain （FDTD） method. The wavefield snapshots vividly illustrate three compressional waves and two shear waves， consistent with Biots theory. Through parameter optimization of the control equation based on measured velocities， numerical velocities are aligned with measured velocities. The results highlight porosity as the most influential factor on the shear stress component of gas hydrates， followed by impacts on hydrates， pore water， and skeleton velocities. Consequently， porosity is best analyzed using the shear stress component of gas hydrates in reservoirs. The skeleton velocity and stress components are less affected by saturation， while the shear stress component of gas hydrates is most affected. Therefore， the optimal choice for analyzing gas hydrate saturation in reservoirs is the shear stress component of gas hydrates.

Keywords：hydrate reservoir visualization; three-phase Biot velocity-stress wave equation; finite difference time domain （FDTD）; porosity; hydrate saturation; perfectly matched layer

海域天然氣水合物是目前最具潛力的能源之一。在其開發過程中，最重要的工作是確定水合物儲層的位置和水合物飽和度，聲波探測［1］是完成這項工作的有效技術手段之一。為了研究聲波在儲層介質中的傳播規律，科學家們提出了各種聲波模型，例如有效介質理論［2］、Biot-Gassmann 模型［3］、三相Biot理論［4］等等。由于水合物儲層被視為由骨架、水合物和孔隙水3種介質構成的多孔介質［5］，因此用三相介質模型研究聲波在水合物儲層的速度與衰減規律，才能分析出三相介質的相關物理參數對聲波的影響。Liu等［6］通過三相介質Biot二階控制方程的特征方程，分析聲波在三相介質中的速度與衰減，得出水合物儲層的物理參數對聲波速度與衰減的影響規律。Gei等［7］把三相介質Biot模型推廣到四相介質，把孔隙液體中包含的氣泡單獨看做一相，考慮氣液混合流體對聲波的影響。上述模型能夠在給定的條件下從理論上分析水合物儲層中的聲波傳輸特征。另外一種分析儲層物理參數對聲波影響的方法是數值模擬。波場響應數值模擬建立在水合物儲層聲波控制方程的數值解之上，目前這方面的科研工作多集中在兩相介質（巖石骨架和孔隙液體）。Yan等［8］分析了兩相介質中薄裂縫帶對反射斯通利波的影響，發現反射斯通利波的振幅隨裂縫的寬度和密度增大而增大，對裂縫的傾角并不敏感。Ou等［9］通過雙相介質波動方程數值分析發現滲透率對斯通利波的影響規律。Carcione等［10］構建三相介質Biot波動方程，并通過波場快照展示了介質中的3種縱波和兩種橫波。但Caricone給出的三相介質Biot波動方程，對應的波速約為5 km/s，遠高于水合物儲層所測數據。因此需要對模型加以改進，以符合水合物儲層的實測波速。波速的主控因素是體積模量、剪切模量和密度。在密度一定的情況下，要校正波速只有通過調節體積模量和剪切模量來實現。傳統三相介質Biot模型，由固結系數反映孔隙固體對儲層骨架體積模量和剪切模量的影響。但是通過Liu等［6］的數值研究發現，固結系數對波速的影響非常微弱，難以描述水合物儲層中速度的復雜變化規律。Carione等［10］使用一種基于實驗數據擬合得到的模量公式，把骨架模量表示成儲層等效壓力的函數，能夠切實反映儲層速度變化規律。數值模擬是分析參數對本構方程影響規律的有效技術手段之一［11-13］。筆者基于三相Biot一階速度應力波動方程對水合物儲層進行數值模擬，使用Carione模量公式表示儲層骨架模量，用遺傳算法對模量參數進行優化，使數值速度與實測速度誤差最小。數值模擬采用的是時空交錯網格上的有限差分（FDTD）算法，時間2階精度，空間4階精度，計算區域使用以微分方程為輔助函數的完全匹配層［14］ （ADEPML）進行截斷。

1 三相介質Biot速度應力波動方程

根據三相Biot理論，水合物儲層的一階速度應力波動方程可以表示為

ρ11si+ρ12wi+ρ13hi+b12（vsi-vwi）+b13（vsi-vhi）=σsij，j，（1）

ρ21si+ρ22wi+ρ23hi+b12（vwi-vsi）+b23（vwi-vhi）=Si，（2）

ρ31si+ρ32wi+ρ33hi+b13（vhi-vsi）+b23（vhi-vwi）=σhij，j，（3）

sij=（K1θs+C12θw+C13θh）δij+2μ1dsij+μ13dhij， （4）

=-φwPw=C12θs+K2θw+C23θh，（5）

hij=（C13θs+C23θw+K3θh）δij+2μ3dhij+μ13dsij.（6）

其中θs=div（vs），θw=div（vw），θh=div（vh）為體應變隨時間變化率，偏應變變化率如下：

dsij=（vsi，j+vsj，i）2-div（vs）δij/3， （7）

dwij=（vwi，j+vwj，i）2-div（vw）δij/3， （8）

dhij=（vhi，j+vhj，i）2-div（vh）δij/3. （9）

式中，vs、vw和vh分別為骨架、孔隙水和水合物的速度向量；

σs和σh分別為骨架和水合物的應力張量;S為與孔隙水壓力成比例的量，本文中在不引起混淆的地方統稱應力。上標s、w和h分別表示關于骨架、孔隙水和水合物的相關變量。下標i，j（i，j=1，2，3，i≠j）表示變量在某個坐標方向上的分量，例如vs1表示骨架在x方向上的速度分量，下標*，i表示函數關于某個坐標求方向導數，例如vs1，1表示函數

vs1關于x的導數。

水合物儲層的彈性常數表示為

K1=［（1-c1）φs］2Kav+Ksm，K2=φ2wKav， （10）

K3=［（1-c3）φh］2Kav+Khm，（11）

C12=（1-c1）φsφwKav， C13=（1-c1）（1-c3）φsφhKav，（12）

C23=（1-c3）φhφwKav， μ1=［（1-g1）φs］2μav+μsm， （13）

μ3=［（1-g3）φh］2μav+μhm，（14）

μ13=（1-g1）（1-g3）φsφhμav+μsh0（φsφh）2.（15）

式中，Ksm、μsm、Khm 、μhm分別為骨架和水合物的體積模量和剪切模量；Kav和μav為三相介質的平均模量。

Kav=（1-c1）φsKs+φwKw+（1-c3）φhKh-1， μav=0.（16）

c1=KsmφsKs， g1=μsmφsKs， c3=KhmφhKh， g3=μhmφhμh .（17）

式中，c1、g1、c3、g3為固結系數。Lee用固結參數α把骨架和水合物模量表示為

Ksm=（1-φw-εφh）Ks1+α（φw+εφh）， μsm=（1-φw-εφh）μs1+αγ（φw+εφh） . （18）

Khm=φhKh1+α（1-φh）， μhm=φhμh1+αγ（1-φh） .（19）

其中

γ=1+2α1+α .

式中，φh和φw分別為水合物和孔隙水的體積占比，并滿足φ=φw+φh。本文中使用儲層的有效壓力來表示儲層骨架的模量

Ksm（pe）=r（1.73+0.23pe-1.7exp（-pe/0.17）），（20）

μsm（pe）=r（0.54+0.06pe-0.54exp（-pe/0.12））.（21）

式中，pe為儲層的等效壓力；r為速度調節系數。

儲層的等效密度表示為

ρ11=α13φsρs+（α12-1）φwρw+（α31-1）φhρh，（22）

ρ22=（α12+α23-1）φwρw，（23）

ρ33=（α13-1）φsρs+（α23-1）φwρw+α31φhρh.（24）

不同相之間的耦合密度表示為

ρ12=-（α12-1）φwρw，ρ23=-（α23-1）φwρw，（25）

ρ13=-（α13-1）φsρs-（α31-1）φhρh.（26）

這里αij表示孔隙空間拓撲結構的彎曲度，

α12=r12φs（φwρw+φhρh）φwρw（φw+φh）+1，（27）

α23=r23φh（φwρw+φsρs）φwρw（φw+φs）+1，（28）

α13=r13φh（φsρs+φhρh）φsρs（φh+φs）+1，（29）

α31=r31φs（φsρs+φhρh）φhρh（φh+φs）+1.（30）

式中，rij為孔隙固體形狀的參數，當孔隙固體是球形時rij=0.5。黏滯系數bij表示為

b12=ηφ2wks， b23=ηφ2wkh，? b13=（1-ε）b013（φhφs）2.（31）

式中，η為孔隙流體黏滯系數；ks和kh分別為骨架和水合物的有效滲透率。

ks=ks0S3r， kh=kh0（φ/φh）2（φw/φs）3.（32）

其中Sr=φw/φ是流體飽和度。

2 數值模擬

要實施FDTD方法，需要把

s、w和h從方程（1）～（3）求解出來，這里給出水合物的第二個速度分量方程，其他兩相的速度分量可以用類似的方法獲得。

h2=［ρ11ρ22（-b13（vh2-vs2）-b23（vh2-vw2）+σh21，1+σh22，2）-ρ12ρ21（-b13（vh2-vs2）-b23（vh2-vw2）+σh21，1+σh22，2）-ρ11ρ32（-b12（vw2-vs2）-b23（vw2-vh2）+S2）+ρ12ρ31（-b12（vw2-vs2）-b23（vw2-vh2）+S2）+ρ21ρ32（-b12（vs2-vw2）-b13（vs2-vh2）+σs21，1+σs22，2）-ρ22ρ31（-b12（vs2-vw2）-b13（vs2-vh2）+σs21，1+σs22，2）］/det（ρ） .（33）

其中det（ρ）為密度矩陣（ρij）的行列式。物理計算區域由300×300個單元構成，并且在外側覆蓋10個單元厚度的PML層。網格單元的長度為0.058 m，時間步長為11.254 μs，總迭代步數為 M=3000，正方形總計算區域的邊長是1.736 m。總計算區域及PML層分布情況見圖1，兩個接收器與激勵源在平行于x軸的同一條直線上，兩個接收器分別離激勵源為50個單元和100個單元。

各相速度分量和應力分量在網格上的位置見圖2。其中Qzσs12、Qxσh11、Qzvs1、Qxvs2、Qxσs12、Qxσh12、Qzvs2、Qzvh2、Qxvs1和Qxvh1是相應分量的PML輔助函數［14］，例如Qzσs12整體是一個變量，表示σs12在z方向上PML層中的輔助函數，其他PML輔助函數可以類似表示。這些輔助函數只定義在PML層中，其他位置為零［15］。

2.1 差分格式

給出差分格式，其中時間方向為二階精度，空間方向為四階精度。為了便于展示，省略了差分格式中的空間坐標，各網格函數的空間坐標可以從圖2對應位置處獲得。

第一步：速度分量更新。

Lτ1=-b12（vs2-vw2）|n-b13（vs2-vh2）|n+（Dxσs12/kx+Qxσs12+Dzσs22/kz+Qzσs22））|n+1/2，（34）

Lτ2=-b12（vw2-vs2）|n-b23（vw2-vh2）|n+（DzS/kz+QzS））|n+1/2，（35）

Lτ3=-b13（vh2-vs2）|n-b23（vh2-vw2）|n+（Dxσh12/kx+Qxσh12+Dzσh22/kz+Qzσh22））|n+1/2，（36）

vs，n+12=vs，n2+dt（D11Lτ1+D12Lτ2+D13Lτ3），（37）

vw，n+12=vw，n2+dt（D21Lτ1+D22Lτ2+D23Lτ3），（38）

vh，n+12=vh，n2+dt（D31Lτ1+D32Lτ2+D33Lτ3）.（39）

式中，|n為網格函數在第n時間層上的數值，表示相關變量的空間坐標;dt為離散時間步長;系數D31=（ρ21ρ32-ρ22ρ31）/det（ρ）從式（33）～（36）得到。Dxσh11為函數σh11沿x方向的四階中心差分格式；Qxσs11為函數σs11在x方向的PML輔助函數。Qxσs11迭代公式如下：

Qxσs，n+3211=-dtdxDxσs，n+1211k2x+（1-dt（dxkx+ax））Qxσs，n+1211.（40）

式中，dx、kx和ax為PML層參數。其他參數定義和變量迭代公式可以類似得到。

第二步：應力分量更新。

θn+1s=Dxvs1kx+Qxvs1+Dzvs2kz+Qzvs2，

θn+1h=Dxvh1kx+Qxvh1+Dzvh2kz+Qzvh2，

θn+1w=Dxvw1kx+Qxvw1+Dzvw2kz+Qzvw2，

dn+111，s=Dxvs1kx+Qxvs1-θs/3，

dn+122，s=Dzvs2kz+Qzvs2-θs/3，

dn+111，h=Dxvh1kx+Qxvh1-θh/3，

dn+122，h=Dzvh2kz+Qzvh2-θh/3，

dn+112，h=（Dzvh1kz+Qzvh1+Dxvh2kx+Qxvh2）/2，

σs，n+3211=σs，n+1211+dt（K1θs+C12θw+C13θh+2μ1d11，s+μ13d11，h），

σs，n+3222=σs，n+1222+dt（K1θs+C12θw+C13θh+2μ1d22，s+μ13d22，h），

σs，n+3212=σs，n+1212+dt（2μ1d12，s+μ13d12，h），

σh，n+3211=σh，n+1211+dt（C13θs+C23θw+K3θh+2μ3d11，h+μ13d11，s），

σh，n+3222=σh，n+1222+dt（C13θs+C23θw+K3θh+2μ3d22，h+μ13d22，s），

σh，n+3212=σh，n+1212+dt（2μ3d12，h+μ13d12，s），

Sn+32=Sn+12+dt（C12θs+K2θw+C23θh）.

格式中的PML輔助函數Qxvh1用如下公式進行迭代更新：

Qxvs，n+11=-dtdxDxvs，n1k2+（1-dt（dxkx+ax））Qxvs，n1.

其他PML輔助函數的迭代公式可以類似得到。

雷克子波源放置在中心單元各主應力分量上

f（t）={1-2［πf0（t-τ0）］2}exp{-［πf0（t-τ0）］2}.

其中τ0=1/f0，主頻f0=1000 Hz，為了壓制數值頻散，本文中采用FCT［16］磨光技術。計算過程中三相Biot波動方程的參數見表1

2.2 波場可視化

二維三相Biot波動方程總共有13個分量，各分量的波場快照見圖3～4，其中所有子圖采用相同色標（色標見圖4）。

根據三相Biot理論，三相Biot波動方程有5種波，3個縱波（每相有一個）和兩個橫波（兩種固相各有一個）。從圖3中可以看出有3個縱波，可以通過波速差異識別出來，在骨架、水合物和孔隙水中分別表現明顯，其中第一縱波在儲層骨架中比較明顯，第二縱波在水合物中表現突出，第三縱波在孔隙水中表現明顯。

兩個橫波在圖4中剪應力分量表現明顯，可以通過不同的波速分別出來，其中第一橫波在骨架中表現明顯，第二橫波在水合物中表現突出。圖3和圖4清楚展現這5種波場，仿真結果符合Biot理論，從而驗證了數值解的有效性。

在圖3和圖4中，看到從上到下發現波形越來越弱，振幅越來越小。也就是說，在骨架中波幅最大，水合物中波幅次之，孔隙水中波幅最小。從而也就解釋了在孔隙介質聲波測速巖石物理實驗中，難以檢測到孔隙水中的縱波的原因，波幅較小，很容易受到噪聲干擾。

2.3 速度調節參數優化

對速度調節參數r，使用遺傳算法對數值速度進行優化，使之與實測速度差最小。

優化方案如下：

（1）取計算區域上兩點作為接收器，與波源在同一條平行于x軸的直線上，見圖1;

（2）計算每個接收器上首波到達時間;

（3）根據兩個接收器上首波到達時間差和兩點間距，計算數值解速度vP，n（r）;

（4）構造目標函數

J（r）=minvP，n（r）-vP，d.

這里vP，d是實測數據［17］;

（5）用遺傳算法求解速度調節參數r。

通過遺傳算法求解，得出當r=1004.2時，數值速度達到vP，d=3215.2（m/s），與實際測速較為接近。在后面的計算中采用本節優化結果。

2.4 孔隙度分析

數值仿真計算可以用來分析水合物儲層相關物理參數對聲波響應的影響。用數值分析的方法研究孔隙度對聲波響應的影響規律。

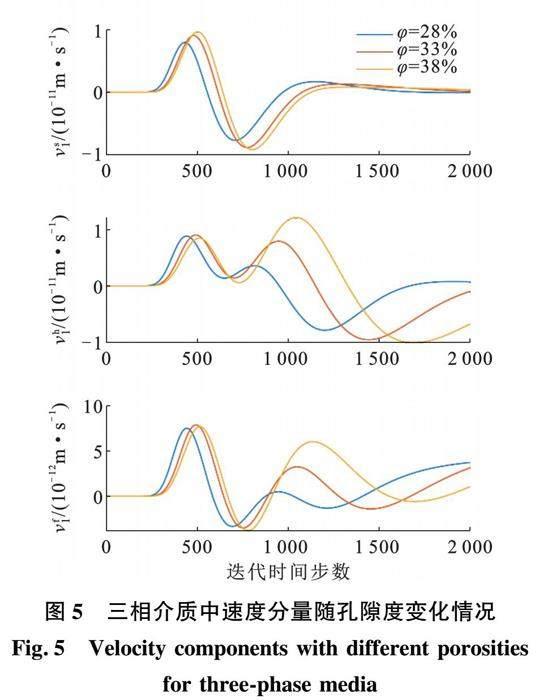
數值分析所采用的參數與前節相同。選取距離激勵源為50個單元的接收器采集數據。各相的速度分量和應力分量隨孔隙度的變化規律見圖5～7。

圖5為三相介質中速度分量隨孔隙度變化情況。從圖中可以看出水合物和孔隙水中的速度分量對孔隙度的變化更加敏感，而儲層骨架中的速度分量對孔隙度的變化不太敏感。而且隨孔隙度變大，三相介質中的速度變慢，但是變慢的幅度逐漸變小。

圖6是三相介質中正應力分量隨孔隙度變化情況。從圖中可以看出儲層骨架和水合物中的正應力分量對孔隙度的變化更加敏感，而孔隙水中的壓力分量對孔隙度的變化不太敏感。

從圖6中前兩個子圖可以看出，儲層骨架中的敏感區間來得更早一些，相對于水合物中的情況來說。而且隨孔隙度變大，三相介質中的正應力變化相速度變慢，但是變慢的幅度逐漸變小。

圖7是儲層骨架和水合物中剪應力分量隨孔隙度變化情況。從圖中可以看出兩相中的剪應力分量對孔隙度的變化都很敏感，比較而言，水合物中敏感區間持續時間長些。

綜合圖5～7可以得出，水合物中剪應力分量對孔隙的變化最為敏感，最適合用來判斷儲層中孔隙度變化情況，其次是水合物儲層中的速度分量。

2.5 飽和度分析

數值分析所采用的參數與前節相同。選取距離激勵源為50個單元的接收器采集數據。各相的速度分量和應力分量隨飽和度的變化規律見圖8～10。

圖8為三相介質中速度分量隨水合物飽和度變化情況。從圖中可以看出水合物和孔隙水的速度分量對飽和度的變化更加敏感，而骨架的速度分量對飽和度的變化不太敏感。而且隨飽和度變大，三相介質中的速度快慢變化很小，不容易分辨。

圖9為三相介質中正應力分量隨水合物飽和度變化情況。從圖中可以看出水合物和孔隙水的正應力分量對飽和度的變化更加敏感，而骨架的正應力分量對飽和度的變化不太敏感。而且隨飽和度變大，三相介質中的速度快慢變化不大。從圖9可以看出，水合物飽和度對水合物的正應力分量和孔隙水的壓力影響最大。

圖10為儲層骨架和水合物中剪應力分量隨水合物飽和度變化情況。從圖中可以看出水合物的剪應力分量對飽和度的變化十分敏感，飽和度為27%時波形幾乎是線性，而飽和度為47%時，波形變化十分劇烈。儲層骨架中的剪應力分量對飽和度的變化，相對于儲層骨架中的速度分量來說，敏感度大些，當飽和度變大時，相速度變大，振幅變大。

圖8～10表明水合物剪應力分量對水合物飽的變化最為敏感，最適合用來定量分析水合物飽和度，其次是水合物儲層中的速度分量。

3 結 論

（1） 數值仿真技術能夠清楚展示三相Biot波動方程的3個縱波和兩個橫波，從而說明數值解的可靠性。

（2）水合物速度分量和剪應力分量對孔隙度的響應更加敏感。

（3）水合物速度分量和剪應力分量對水合物飽和度的響應更加敏感。水合物剪應力分量是用來定量分析儲層孔隙度和水合物飽和度的最佳技術手段。

參考文獻：

［1］ WANG X H， XU Q， HE Y N， et al. The acoustic properties of sandy and clayey hydrate-bearing sediments［J］. Energies，2019，12（10）：1-11.

［2］ HELGERUD M B， DVORKIN J， NUR A， et al. Elastic-wave velocity in marine sediments with gas hydrates： effective medium modeling［J］. Geophysical Research Letters， 1999，26（13）：2021-2024.

［3］ LEE M W. Modified Biot-Gassmann theory for calculating elastic velocities for unconsolidated and consolidated sediments［J］. Marine Geophysical Researches， 2002，23（5）：403-412.

［4］ LEE M W， COLLETT T S. Elastic properties of gas hydrate-bearing sediments［J］. Geophysics， 2001，66（3）：763-771.

［5］ LECLAIRE P H， COHEN-TNOUDJI F，AGUIRRE-PUENTE J. Extension of Biots theory of wave propagation to frozen porous media［J］. The Journal of the Acoustical Society of America， 1994，96（6）：3753-3768.

［6］ LIU L， ZHANG X， WANG X. Wave propagation characteristics in gas hydrate-bearing sediments and estimation of hydrate saturation［J］. Energies， 2021，14（4）：804.

［7］ GEI D， CARCIONE J M， PICOTTI S. Seismic rock physics of gas-hydrate bearing sediments

［M］//MIENERT J， BERDT C， TREHO A M， et al. World Atlas of Submarine Gas Hydrates in Continental Margins， Cham： Springer，? 2022：55-63.

［8］ YAN S G， XIE F L， GONG D， et al. Borehole acoustic fields in porous formation with tilted thin fracture［J］. Chinese Journal of Geophysics， 2015，58（1）：307-317.

［9］ OU Weiming， WANG Zhuwen. Simulation of Stoneley wave reflection from porous formation in borehole using FDTD method［J］. Geophysical Journal International， 2019，217（3）：2081-2096.

［10］ CARCIONE J M， SERIANI G. Wave simulation in Frozen porous media［J］. Journal of Computational Physics， 2001，170（2）：676-695.

［11］ 范翔宇，么勃衛，張千貴，等.基于聲波信號預測Kaiser應力點的水平地應力［J］.西南石油大學學報（自然科學版），2022，44（2）：40-48.

FAN Xiangyu， YAO Bowei， ZHANG Qiangui， et al. Study on the calculated method of horizontal in-situ stress based on the Kaiser stress point predicted by acoustic signal［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2022，44（2）：40-48.

［12］ 鄭多明，汪家洪，肖又軍，等. 基于地震數值模擬的溶洞型儲層地震特征分析［J］. 西南石油大學學報（自然科學版），2023，45（6）：57-68.

ZHENG Duoming， WANG Jiahong， XIAO Youjun， et al. Seismic characteristics analysis of karst cavity reservoirs based on seismic numerical simulation［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（6）：57-68.

［13］ 張濤，孫天禮，陳偉華，等.不同孔-縫-洞組合碳酸鹽巖儲層氣水兩相孔隙尺度流動模擬［J］.西南石油大學學報（自然科學版），2023，45（5）：88-96.

ZHANG Tao， SUN Tianli， CHEN Weihua， et al. Pore-scale simulation of gas-water two phase flow in carbonate reservoir with different combinations of pore， network and hole［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（5）：88-96.

［14］ MARTIN R， KOMATITSCH D， GEDNEY S D， et al. A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary differential equations（ADE-PML） ［J］. Computer Modeling in Engineering and Sciences， 2010，56（1）：17-40.

［15］ 楊書博，趙琪琪，王磊，等.基于柱坐標系復頻移完全匹配層的隨鉆套管井聲場有限差分模擬［J］.中國石油大學學報（自然科學版），2022，46（1）：62-71.

YANG Shubo， ZHAO Qiqi， WANG Lei， et al. Finite difference modeling of acoustic fields in cased holes under LWD conditions based on CFS-NPML in a cylindrical coordinate system［J］. Journal of China University of Petroleum（ Edition of Natural Science），2022，46（1）：62-71.

［16］ HUANG M X， XUE T X， WANG Y X. Seismic wave field simulation on the symplectic and FCT algorithm［J］. Progress in Geophysics， 2015，30（2）：565-570.

［17］ LIU J， ZHANG J， MA F，? et al. Estimation of seismic velocities and gas hydrate concentrations： a case study from the Shenhu area， northern South China Sea［J］. Marine and Petroleum Geology， 2017，88：225-234.

（編輯 修榮榮）

基金項目：CNPC重大專項（ZD2019-184-001）; 中央高校基本科研業務費專項（20CX05011A）;國家自然科學基金項目（42174142，42374152，41404091）;山東省自然科學基金項目（ZR2023YQ034，ZR2020MD050）;中國石油科技創新基金項目（2021DQ02-0402）

第一作者及通信作者：石仁剛（1978-），男，講師，博士，研究方向為波場模擬與成像。E-mail：shirg@upc.edu.cn。

引用格式：石仁剛，魏周拓，葛新民，等.基于三相Biot速度應力波動方程的水合物儲層波場數值模擬［J］.中國石油大學學報（自然科學版），2024，48（3）：57-64.

SHI Rengang， WEI Zhoutuo， GE Xinmin， et al. Numerical simulation of hydrate reservoir based on three-phase Biot velocity-stress wave equaiton ［J］. Journal of China University of Petroleum （ Edition of Natural Science ）， 2024，48（3）：57-64.