基于極端梯度提升算法的地震同相軸自動識別

黃建平 張若楓 高睿語 李亞林 段文勝 陳飛旭 郭廷超 潘成磊

摘要：在常規地震同相軸識別方法基礎上，通過引入極端梯度提升算法（XGBoost）智能化策略，并結合地震數據相鄰道相似性特征，發展一種基于極端梯度提升算法的地震同相軸自動識別技術方法。在編程實現方法的基礎上，通過簡單層狀模型和復雜Marmousi模型模擬的記錄進行測試，驗證方法的正確性。對含噪音數據和實際資料中的同相軸進行識別測試，同時進行單道對比定量分析以及不同信噪比情況下算法預測結果精度對比。結果表明：新方法對含噪數據和實際資料均具有較好的適應性；在低信噪比（-6.98 dB）情況下，同相軸的查準率仍可超過90%。

關鍵詞： 同相軸拾取； 機器學習； 特征拾取； 極端梯度提升算法

中圖分類號：P 631.4?? 文獻標志碼：A

文章編號：1673-5005（2024）03-0044-13?? doi：10.3969/j.issn.1673-5005.2024.03.005

Automatic detection of seismic event based on eXtreme gradient boosting

HUANG Jianping1， ZHANG Ruofeng1， GAO Ruiyu2，? LI Yalin3， DUAN Wensheng3，CHEN Feixu3， GUO Tingchao4， PAN Chenglei4

（1.School of Geosciences in China University of Petroleum（East China）， Qingdao 266580， China;2.SINOPEC Geophysical Research Institute， Nanjing 211100， China;3.Tarim Oilfield Branch， CNPC， Korla 841000， China;4.Geophysical Prospecting Research Institute of Jiangsu Oilfield Company， SINOPEC，Nanjing 210046， China）

Abstract： This paper presents an automatic seismic event detection method based on eXtreme gradient boosting （XGBoost） by integrating intelligent strategies and leveraging the similarity characteristics of adjacent traces in seismic data. The proposed method is validated through programming and testing on both simple layered and complex Marmousi models. The detection tests conducted on noisy data and the real data demonstrate the methods robustness and adaptability， even in low signal-to-noise ratio （SNR）conditions （-6.98 dB），? achieving a seismic event detection precision of 90%. Additionally， single channel contrast quantitative analysis and comparison of algorithm prediction accuracy under various SNR conditions further confirm the methods feasibility and applicability.

Keywords：event picking； machine learning； feature picking； eXtreme gradient boosting

在地震數據處理過程中，同相軸的識別對于目的層追蹤、走時類反演、特定目標體成像等研究至關重要［1-3］。由于地震信號中偏移距、目的層深度、信噪比等諸多因素的影響，同相軸能量差異較大，同相軸準確識別和檢測較為困難，且野外數據采集數據量大，需要大量的人工成本進行數據拾取。因此研究高精度、高效率、高自動化的同相軸自動識別方法極為重要。

根據檢測方法的差異，傳統地震同相軸自動識別方法主要分為兩大類。第一類方法為直接檢測法，該類方法主要通過對地震記錄進行信號分析提取地震同相軸，利用地震波具備的屬性與特征提取地震同相軸。Allen［4］提出的反映信號瞬時能量變化的長短時能量比（STA/LTA）方法，基于能量分析，使用廣泛，實現原理簡單高效，當比值超出給定閾值后可以確定出同相軸位置。其缺點是閾值的選取范圍難以明確和對突變振幅信息敏感。Hatherly等［5-6］利用一些統計標準，通過計算頻率帶寬、窗口大小和平滑參數上來提高同相軸拾取精度。魏巍等［7］提出了采用自適應噪聲抵消方法來識別檢測微地震信號，獲得高精度識別結果，但是其收斂速度較慢，提取的信號頻帶較窄。Moore等［8］提出基于波譜包絡的初至震相檢測，將貝葉斯推理應用至地震軌跡的生成概率模型，提高信號靈敏度和定位性能。

這類方法主要采用優化的信號特征作為有效信號判斷標準，提高了檢測識別性能，但其計算量大，泛化能力較差，信號在復雜背景噪聲中難以用特定單一特征衡量。第二類方法為模板匹配法，該類方法主要是選取預設的模板、相同長度待識別波形并進行相關度計算，根據計算結果進行同相軸檢測。Gibbons等［9-11］利用基準同相軸信號，通過計算互相關函數拾取具有高度相似性的目標信號。Mena等［12］采用傅里葉變換分析窗函數寬度與地震震級的關系，但窗口大小固定且選取較難，可復現性較差。隨后，Ghaffazadeh等［13］基于S時頻變換脈沖震動識別法，實現了利用卷積S變換的時頻濾波識別地震信號。這類模板匹配方法基準同相軸的選取困難，往往具有較大人為主觀性和較差的魯棒性，與基準同相軸相似的目標信號往往同最終結果有所偏差。隨著計算機和人工智能技術的逐漸成熟，人工智能方法作為一種全新的全局優化類型算法逐漸被應用于地震勘探中［14-16］，人工智能方法進行同相軸自動識別也是其中的一個典型應用。Albert等［17-20］基于神經網絡算法自動拾取地震同相軸信號，驗證了深度學習方法的有效性。除了神經網絡方法之外，其他機器學習算法也得到了很多應用。趙爭光等［21］使用監督機器學習算法從噪聲中分離微地震信號，其訓練的支持向量機模型識別準確率可達90%。戴永壽等［22-23］利用CEEMD算法和遞歸最小二乘結合提取了時變混合相位小波，其精度較之傳統時變小波提取方法有一定改善。陳陽康［24］使用機器學習聚類方法實現微地震同相軸初至拾取，拾取精度優于長短時能量對比法。圍繞西部探區地震數據中噪聲種類復雜、信噪比低、保真度差、層間多次波發育、同相軸拾取困難的難題，筆者基于極端梯度學習算法［25-27］提出一種適應于低信噪比數據的地震同相軸自動識別技術方法，并在編程實現方法的基礎上，通過模型和實際資料試處理，來驗證該方法對西部典型數據的適應性。

1 XGBoost方法原理

極端梯度提升（eXtreme gradient boosting）算法簡稱XGBoost，由陳天奇等［28］

基于集成學習方法提出。該算法相對于單一決策樹來說，訓練過程較為穩定且泛化能力較好，在機器學習和數據挖掘等方面應用廣泛。XGBoost是集成學習方法的一種，它是以分類回歸樹（CART樹）進行組合。其中決策樹預測模型可表示為

i=∑Kk=1fk（xi）. （1）

式中，K為樹的總個數；fk為第k顆樹的預測結果；xi為第i個樣本；i為樣本xi的總預測值。

為了防止過擬合，XGBoost的目標函數由損失函數和復雜度組成，復雜度由葉子數量和L2正則項組成。對于目標函數表示為

Obj（θ）=∑ni=1l（yi，i）+∑Kk=1Ω（fk）.（2）

式中，l（yi，i）為樣本xi的訓練誤差即損失函數，一共n個樣本；Ω（fk）為第k顆樹的復雜度。

XGBoost遵循決策樹架構的疊加式訓練：

y（0）i=0，y（1）i=f1（xi）=y（0）i=+f1（xi），y（2）i=f1（xi）+f2（xi）=y（1）i+f2（xi），

……

y（k）i=y（k-1）i+fk（xi）.（3）

即k個模型的預測值等于k-1個模型與正在訓練的第k個模型的預測值之和。

此時將XGBoost的目標函數寫為

Obj（θ）=∑ni=1

l（yi，i）+∑Kk=1Ω（fk）=∑ni=1

l（yi，ki）+∑Kk=1Ω（fk）=∑ni=1

l（yi，k-1i+fk（xi））+∑K-1k=1Ω（fk）+Ω（fk）.（4）

式中，k-1i為前k-1次總預測值，為常數；fk（xi）為第k次數的預測結果;∑K-1k=1Ω（fk）為前k-1次所有樹正則化項取值之和;Ω（fk）為第k次中數的正則化項取值。Ω（fk）表示為

Ω（fk）=γT+12λω2.（5）

式中，γ為懲罰力度；T為葉子的個數;ω為與真實值的殘差；12λω2為L2正則項，將它加在目標函數中，可以防止過擬合。

XGBoost是眾多機器學習算法的一種，因此在訓練時也需要進行調參。較為重要的參數有eta、max_depth、min_child_weight、subsample。eta為學習速率，更新過程中用到的收縮步長，在每次計算之后，算法會獲得新特征的權重。eta通過縮減特征的權重使提升計算過程更加穩定；max_depth為樹的最大深度，值越大越容易過擬合；min_child_weight決定最小葉子節點樣本權重和，加權和低于此參數時不再分裂產生新的葉子節點。當其值較大時可避免模型學習到局部的特殊樣本；subsample參數表示控制對每棵樹隨機采樣的比例。

本文中還采用了10折交叉驗證法對參數進行調整，即把訓練數據集隨機平均分為10份互斥子集，選擇其中9份作為訓練集，剩下的1份作為測試集。將這一過程重復10次且每次從中選取不同測試集，將10次計算結果取均值作為最終參數選定得分結果。此方法可以一定程度上減小過擬合，如圖1所示。

2 模型測試

在本文所述流程（圖1）中，將其分為5步，即數據準備（訓練與測試數據集）、特征提取、特征選擇、模型訓練、數據測試（預測）。一般情況下，在工業中步驟相對固定，通常以管道（pipeline）形式存在，使數據與產品相似，通過流水線一樣將預測結果生產出來。

2.1 數據準備

本文中使用正演模擬炮記錄和實際地震數據作為訓練數據集。訓練數據集一為模擬正演炮記錄，速度模型為層狀模型，第一層速度為2500 m/s，第二層速度為2000m/s。模型橫向采樣點為401，縱向采樣點2501，網格間距為10 m。本文中采用主頻為30 Hz的零相位雷克子波，正演時間采樣步長為0.5 ms。訓練數據集二也為模擬正演炮記錄，速度模型為Marmousi模型，最大速度為5000 m/s，最小速度1500m/s。橫向采樣點為701，縱向采樣點4501，網格間距為5 m。同樣采用主頻為30 Hz的零相位雷克子波，正演時間采樣步長為0.4 ms。訓練數據集三為某研究區實際地震數據。

信噪比計算公式為

RSN=101gPsignalPnoise.（6）

式中，Psignal為有效信號功率；Pnoise為含噪信號功率。對正演模擬炮記錄添加信噪比為-6.98 dB的隨機高斯白噪后，背景噪聲場噪聲干擾強烈，有效信號淹沒于背景噪聲中。特別是振幅較小且所處位置過于密集的信號，由人工肉眼觀察已無法識別，弱信號幾乎完全被噪聲場所屏蔽，層位信息更是無法準確識別。因此在信噪比較低的地震數據中開發基于智能算法的有效信號識別技術具有十分重要的價值。

將訓練數據（單道模擬地震記錄）分段，經過測試后每段長度設置為116，這樣可以提高識別同相軸的縱向識別率。分段后，將訓練數據標記為兩類，分別用“0”和“1”作為標簽分類，其中“0”代表噪聲信號，“1”代表有效信號（同相軸）。其中層狀模型正演炮記錄篩選出75865條噪聲信號數據和6834條同相軸信號數據，這82699條數據構成了層狀模型所需訓練數據總和；Marmousi模型正演炮記錄篩選出95463條噪聲信號數據和28638條同相軸信號數據，共計124101條數據組成了Marmousi模型所需的訓練數據總和。在得到分段劃分并貼好標簽的數據后，將數據從輸入空間轉化到特征空間。

為了最大程度上利用分段地震記錄所包含的信息，綜合參考了趙爭光等［21］和Attenberg等［29］的研究，共設計191個特征。其中包含63個單道特征（一維特征）和128個道間特征（二維特征）。利用特征工程（特征提取和選擇）中生成的特征對訓練數據做進一步的優化。層狀模型和Marmousi模型對應篩選出的二維特征如圖6所示。

從圖6中可看出，經過了灰度共生矩陣（GLCM）處理，炮記錄中的有效信號與噪聲相對比，其清晰程度有所改善，則可表明GLCM計算能夠反映信號的清晰程度以及加強紋理溝紋深淺對比。

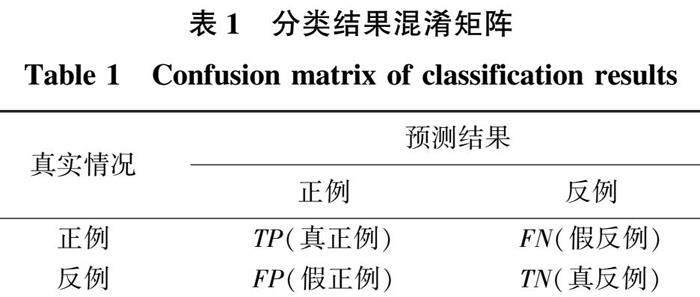
對于噪聲與同相軸信號這種二分類問題，可以根據真實標簽和通過模型預測得到的標簽數據集劃分為真正例（true positive）、假正例（false positive）、真反例（true negative）、假反例（false negative）4種情況，令TP、FP、TN、FN分別表示其對應的樣例數，有TP+FP+TN+FN=S（樣例總數），如表1所示。此外，查準率（p）和查全率（r）以及F1度量分別定義為

p=TPTP+FP ，（7）

r=TPTP+FN ，（8）

F1=2prp+r=2TPS+TP-TN .（9）

2.2 模型測試

為測試XGBoost機器學習算法自動識別地震同相軸對等效地震地質模型的有效性與普適性，本文中使用與訓練數據集相對應的正演模擬炮記錄作為測試數據集。測試數據集一為層狀模型正演炮集中兩個單炮，炮記錄橫向采樣點為401，縱向采樣點為7001，采樣間隔為0.5 ms，網格間距為8 m。測試數據集二為Marmousi模型正演炮記錄，其中單炮記錄一（圖7（a））橫向采樣點為501，縱向采樣點7001，采樣間隔為0.4 ms，網格間距為10 m；單炮記錄二（圖7（b））橫向采樣點為596，縱向采樣點4500，采樣間隔為0.5 ms，網格間距為8 m。對加入信噪比為-6.98 dB的隨機噪聲后的測試數據均進行自動識別。同時對層狀模型正演炮記錄加入不同信噪比的噪聲進行噪聲強度測試。

針對層狀模型正演炮記錄，即使在信噪比極其低的情況下，不管是直達波還是反射波，使用XGBoost算法識別到的同相軸信號都清晰完整，而使用STA/LTA方法識別到的同相軸信號效果較差，且噪聲并沒有被完全識別出，如圖7所示。對XGBoost識別結果分別抽取數據集（圖7（a））：炮檢距1200 m處、2040 m處單道炮記錄（圖8（a））；抽取數據集（圖7（b））：炮檢距728 m處、2144 m處單道炮記錄（圖8（b））。

Marmousi模型較為復雜，其正演炮記錄同相軸較密集。對其加入信噪比為-6.98 dB的隨機噪聲后，由圖9可以看出，使用XGBoost方法直達波同相軸可完全識別，反射波中雖有部分斷裂，但識別總體效果較好，能量較強的信號可以完全識別出來；而STA/LTA識別效果可明顯看出同相軸斷裂嚴重，噪聲信號識別不全。對XGBoost識別結果分別抽取數據集（圖9（a））：炮檢距1050 m處單道炮記錄、炮檢距3980 m處單道炮記錄（圖10（a））；抽取數據集（圖9（b））：炮檢距1696 m處單道炮記錄、炮檢距3816 m處單道炮記錄（圖10（b））。

在實際中，地震同相軸自動識別常用于初至自動拾取，對拾取速度要求較高。將XGBoost算法與STA/LTA方法識別時間分別記錄后如表2（41炮處理總時間）所示。由表2可知：XGBoost機器學習算法在不同模型中的識別效率較之常規STA/LTA方法稍有改善。通過訓練過程及識別結果得到相應反饋如表3所示。綜合以上測試結果可知：無論是層狀模型還是復雜Marmousi模型，XGBoost機器學習算法識別效果均優于傳統STA/LTA算法。其原因在于，傳統STA/LTA算法僅利用地震信號的時間窗和時間窗類的平均噪聲，而本文所述方法為機器學習算法流程，在已有的地震數據191個特征的基礎上進行特征選擇，選出最優特征后使用XGBoost算法進行訓練，最大程度上使用了地震數據有效信息。

由表3可知：對于噪聲而言查準率要低于其查全率，對于同相軸而言查全率要低于查準率。由式（7）和 （8）所知，查準率和查全率是一對矛盾的度量。一般來說，查準率高時查全率往往偏低，而查全率高時查準率往往偏低。但對于本文所述二分類問題，即分出噪聲和同相軸，查準率和查全率可同時較高。一方面需要盡可能多的將噪聲有效剝離，因此對噪聲而言查全率比查準率重要；另一方面，需要識別出高精度的有效信號，盡量避免假有效信號的出現，因此對同相軸而言查準率比查全率重要。

2.3 噪聲強度測試

為了證明XGBoost算法訓練得到的模型效果的穩定性、有效性和泛化能力，在測試數據層狀模型正演單炮記錄（圖7（b））的基礎上進行噪聲強度測試，根據式（6）依次添加-10、-6.98、-5.23、-3.01、-0.97、1.76 dB強度的噪聲作為測試數據，測試結果如表4所示。對其抽取炮檢距2144 m處共偏移距記錄，可看出在不同的信噪比情況下XGBoost模型均可以準確地識別出同相軸信號。即使在信噪比-10 dB的極端情況下，層狀模型同相軸已經完全被噪聲所淹沒覆蓋，依然可以被完整檢測到，同相軸查準率依然超過85%，代價僅為存在極少量誤檢測信號。結果如圖11所示。

3 實際數據測試

在驗證本文所述方法正確性和有效性的基礎上，為進一步驗證XGBoost機器學習算法自動識別的適應性，選取某研究區僅去掉面波后的炮記錄，使用相應實際炮記錄人工標定后作為訓練集進行訓練，利用得到的XGBoost算法訓練模型進行有效同相軸信號拾取，測試結果如圖12所示。圖12（a）為原始炮記錄，圖12（b）為測試結果，從圖中可看出初至波和直達波能被完整識別，箭頭所指附近反射波信號大多都能拾取，但同相軸極密集的地方有斷裂。原因是該記錄信噪比較低且同相軸密集，振幅不強；噪聲種類眾多，很難區分所有噪聲特征與有效同相軸特征；在原始地震數據基礎上人工標定難度較大且標定人員標準有所不同。該實際地震數據由XGBoost模型自動識別性能反饋為：查準率為90%，查全率為88%，F1度量為89%。綜上，本文中所訓練XGBoost機器學習算法模型具備較強性能，且識別效果與人工標定訓練數據結果具有較強關聯。

另選取某實際地震資料部分成像剖面進行同相軸層位追蹤測試，同樣使用對應的實際數據人工標定后進行訓練。該部分為地震資料成像剖面的中深層區域，如圖13所示。從圖14測試結果與原始剖面對比可看出，本文訓練的XGBoost模型可以完整

4 結束語

傳統STA/LTA方法的識別精確度與效率均弱于XGBoost機器學習算法。

本文方法具有較強抗噪性，即使在信噪比為-10 dB的極端情況下仍可檢測到有效信號。對于復雜模型與實際地震資料而言，為了實現可靠穩定的同相軸拾取精度，需要更加精準且精細標簽的訓練樣本。

參考文獻：

［1］ LI C， HUANG J P， LI Z C， et al. Plane-wave least-squares reverse timemigration with aprecon-ditioned stochastic conjugate gradient method［J］. Geophysics，2018，83（1）：33-46.

［2］ WANG Z， HUANG J P， LI Z C， et al. Velocity model estimation of karstic fault reservoirs using full waveform inversion accelerated on GPU［J］. Interpretation，2020，8（4）：191-203.

［3］ 黃建平，張入化，國運東，等.基于Seislet分數階閾值算法約束的平面波最小二乘逆時偏移［J］.中國石油大學學報（自然科學版），2020，44（3）：26-37.

HUANG Jianping， ZHANG Ruhua， GUO Yundong， et al. Plane-wave least-square reverse time migration with Seislet fractional threshold algorithm constraint［J］.Journal of China University of Petroleum （Edition of Natural Science），2020，44（3）：26-37.

［4］ ALLEN R V. Automatic earthquake recognition and timing from single traces［J］. GeoScience World，1978，68（5）：1521-1532.

［5］ HATHERLY P J. A computer method for determining seismic first arrival times［J］. Geophysics，1982，47（10）：1431-1436.

［6］ BAILLARD C， CRAWFORD W C， BALLU V， et al. An automatic kurtosis-based P- and S-phase picker designed for local seismic networks［J］. Bulletin of the Seismological Society of America，2013，104（1）：394-409.

［7］ 魏巍，劉學偉.自適應噪聲抵消技術在地震資料處理中的應用［J］.石油天然氣學報，2008（4）：79-83，175.

WEI Wei， LIU Xuewei. Application of adaptive noise cancellation technique in seismic data processing ［J］.Journal of Oil and Gas Technology，2008（4）：79-83，175.

［8］ MOORE D A， MAYEDA K， MYERS S， et al. Progress in signal-based Bayesian monitoring［C］//Proceedings of the 2012 Monitoring Research Review： Ground-based Nuclear Explosion Monitoring Technologies. Arizona： National Nuclear Security Administration，2012.

［9］ GIBBONS S J， RINGDAL F. The detection of low magnitude seismic events using array-based waveform correlation［J］. Geophysical Journal International，2006，165（1）：149-166.

［10］ MAVROEIDIS G P， PAPAGEORGIOU A S. A mathematical representation of near-fault ground motions［J］.Bulletin of the Seismological Society of America， 2003，93（3）：1099-1131.

［11］ 馮雪玲，劉東亞，李志海.基于小波互相關的微地震信號檢測方法研究［J］.大地測量與地球動力學，2019，39（9）：982-986.

FENG Xueling， LIU Dongya， LI Zhihai. Research on microseismic signal detection method based on wavelet cross-correlation［J］.Journal of Geodesy and Geodynamics，2019，39（9）：982-986.

［12］ MENA B， MAI P M. Selection and quantification of near-fault velocity pulses owing to source irectivity［J］. Georisk， 2011，5（1）：25-43.

［13］ GHAFFARZADEH H. A classification method for pulse-like ground motions based on S-transform［J］.Natural Hazards， 2016，84（1）：335-350.

［14］ WU Xinming， SHI Yunzhi， FOMELS， et al. FaultNet3D： predicting fault probabilities， strikes， and dips with a single convolutional neural network［J］. IEEE Trans Geoscience and Remote Sensing，2019，57（11）：9138-9155.

［15］ 劉學鋒，張曉偉，曾鑫，等.采用機器學習分割算法和掃描電鏡分析頁巖微觀孔隙結構［J］.中國石油大學學報（自然科學版），2022，46（1）：23-33.

LIU Xuefeng， ZHANG Xiaowei， ZENG Xin， et al. Pore structure characterization of shales using SEM and machine learning based segmentation method［J］.Journal of China University of Petroleum（ Edition of Natural Science），2022，46（1）：23-33.

［16］ GAO Z， HU S， LI C， et al. A deep-learning-based generalized convolutional model for seismic data and its application in seismic deconvolution［J］. IEEE Transactions on Geoscience and Remote Sensing， 2021，60：1-7.

［17］ ALBERTS P， WARNER M， LISTER D. Artificial neural networks for simultaneous multi horizon tracking across discontinuities［C］//SEG Technical Program Expanded Abstracts. Calgary： Society of Exploration Geophysicists， c2000：651-653.

［18］ AKRAM J， OVCHARENKO O， PETER D. A robust neural network-based approach formicroseismic event detection［C］//SEG Technical Program Expanded Abstracts.Houston， Texas： SEG， c2017：2929-2933.

［19］ DEBOTYAM M， FRED A， MARTIN K. Novel hybrid artificial neural network based autopicking workflow for passive seismic data［J］. Geophysical Prospecting，2014，62（4）：834-847.

［20］ YUAN S， LIU J， WANG S， et al. Seismic waveform classification and first-break picking using convolution neural networks［J］. IEEE Geoscience and Remote Sensing Letters， 2018，15（2）：272-276.

［21］ ZHAO Z， GROSS L. Using supervised machine learning to distinguish microseismic from noise events［C］//SEG Technical Program Expanded Abstracts. Houston： SEG， c2017：2918-2923.

［22］ 戴永壽，張鵬，萬勇，等.時變子波提取及其在地震資料智能處理中的應用［J］.中國石油大學學報（自然科學版），2020，44（6）：28-35.

DAI Yongshou， ZHANG Peng， WAN Yong， et al. Time-varying wavelet extraction and its application in intelligent processing of seismic data［J］.Journal of China University of Petroleum （Edition of Natural Science），2020，44（6）：28-35.

［23］ ZHANG P， DAI Y， ZHANG H， et al. Combining CEEMD and recursive least square for the extraction of time-varying seismic wavelets［J］. Journal of Applied Geophysics， 2019（170）：103854.

［24］ CHEN Yangkang. Automatic microseismic event picking via unsupervised machine learning［J］. Geophysical Journal International，2020，222（3）：1750-1764.

［25］ 潘少偉，王朝陽，張允，等. 基于長短期記憶神經網絡補全測井曲線和混合優化XGBoost的巖性識別［J］.中國石油大學學報（自然科學版），2022，46（3）：62-71.

PAN Shaowei， WANG Zhaoyang， ZHANG Yun， et al. Lithology identification based on LSTM neural networks completing log and hybrid optimized XGBoost［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2022，46（3）：62-71.

［26］ 彭更新，徐峰，徐凱馳，等.基于寬頻子波的檢波組合目標函數優化方法［J］.西南石油大學學報（自然科學版），2023，45（2）：32-42.

PENG Gengxin， XU Feng， XU Kaichi， et al. An objective function optimization method based on multi-frequency wavelets for receiver combination in seismic acquisition［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（2）：32-42.

［27］ 鄭多明，汪家洪，肖又軍，等.基于地震數值模擬的溶洞型儲層地震特征分析［J］.西南石油大學學報（自然科學版），2023，45（6）：57-68.

ZHENG Duoming， WANG Jiahong， XIAO Youjun， et al. Seismic characteristics analysis of karst cavity reservoirs based on seismic numerical simulation［J］. Journal of Southwest Petroleum University（Science & Technology Edition）， 2023，45（6）：57-68.

［28］ CHEN T Q， GUESTRIN C.? XGBoost： a scalable tree boosting system［C/OL］//Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining，San Francisco， CA， USA， 13-17 August 2016［2022-08-20］. https：//doi.org/10.1145/2939672.2939785.

［29］ ATTENBERG J M， IPEIROTIS P G， PROVOST F J. Methods， systems， and media for identifying errors in predictive models using annotators： U.S. Patent 9，311，599［P］. 2016-04-12.

（編輯 修榮榮）

基金項目：國家重點研發計劃項目（2019YFC0605503）;國家自然科學基金優秀青年科學基金項目（41922028）;國家自然科學基金創新研究群體基金項目（41821002）;山東省科研機構運費等專項（2021QNLM020001-5）

第一作者及通信作者：黃建平（1981-），男，教授，博士，研究方向為地震波正演及偏移成像方法。E-mail：jphuang@upc.edu.cn。

引用格式：黃建平，張若楓，高睿語，等.基于極端梯度提升算法的地震同相軸自動識別［J］.中國石油大學學報（自然科學版），2024，48（3）：44-56.

HUANG Jianping， ZHANG Ruofeng， GAO Ruiyu， et al. Automatic detection of seismic event based on eXtreme gradient boosting［J］.Journal of China University of Petroleum（ Edition of Natural Science），2024，48（3）：44-56.