數字音頻信號處理中的主動降噪方法

牛怡琴

【摘要】本文針對數字音頻信號處理中的主動降噪問題展開了研究。首先，通過探討LMS算法的基本原理，分析了其在降噪任務中的應用及局限性。然后，提出了自適應正則化技術，增強了算法在非平穩噪聲環境下的性能和穩定性。最后，利用NOISEX-92數據集對所提出的優化方法進行了實驗驗證，結果表明優化后的方法在信噪比（SNR）和均方根誤差（RMSE）等評價指標上取得了顯著的改善，表明自適應正則化技術對提高LMS算法在數字音頻信號處理中的主動降噪效果具有重要意義。

【關鍵詞】音頻處理；主動降噪；最小均方算法；正則化技術

中圖分類號：G212? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? DOI：10.12246/j.issn.1673-0348.2024.11.043

數字音頻信號處理作為數字信號處理領域中的一個重要分支，在當今社會中扮演著越來越關鍵的角色[1]。然而，由于傳感器本身的特性以及環境噪聲等因素的影響，數字音頻信號往往會受到不同程度的干擾，從而削弱了信號的質量和清晰度。因此，研究數字音頻信號的主動降噪方法對于提升信號處理的效能和性能具有重要的理論和實踐價值。

國內外學者們在數字音頻信號處理領域開展了大量的研究工作，囊括了傳統的降噪方法以及基于機器學習和深度學習的新興技術。傳統的降噪方法主要包括基于統計特性的方法和基于濾波器的方法。其中，最小均方（Least Mean Square，LMS）算法作為一種經典的自適應濾波器算法，被廣泛應用于數字音頻信號的降噪任務中。然而，傳統的LMS算法在處理非平穩噪聲時存在收斂速度慢、穩定性差等問題，難以滿足實際應用的需求[2]。

本文深入研究了數字音頻信號處理中的主動降噪方法。首先，對最小均方主動降噪方法的基本原理進行了探討。其次，引入自適應正則化技術對LMS算法進行了優化，以期提高其在降噪任務中的性能。最后，采用NOISEX-92數據集對所提出的優化方法進行了測試和評估，驗證其在實際應用中的有效性和可行性。通過本文的研究，旨在為數字音頻信號處理領域的相關研究和實際應用提供理論指導和技術支持。

1. 最小均方主動降噪方法的基本原理

LMS主動降噪方法是一種經典的自適應濾波器算法，用于數字音頻信號處理中的降噪任務。假設有一個長度為N的濾波器w[n]，其輸出y[n]與輸入信號x[n]之間的關系可以用卷積運算表示：

（1）

其中，w[k]是濾波器的系數（1），n是當前時刻，k是濾波器的時延。LMS算法的目標是通過不斷調整濾波器的系數w[k]，使得濾波器的輸出y[n]盡可能地接近期望的信號d[n]。因此，LMS算法可以描述為以下迭代更新規則：

（2）

其中，w[n]是濾波器的系數向量，μ是步長參數，e[n]=d[n]-y[n]是估計的誤差信號，d[n]是期望的信號。

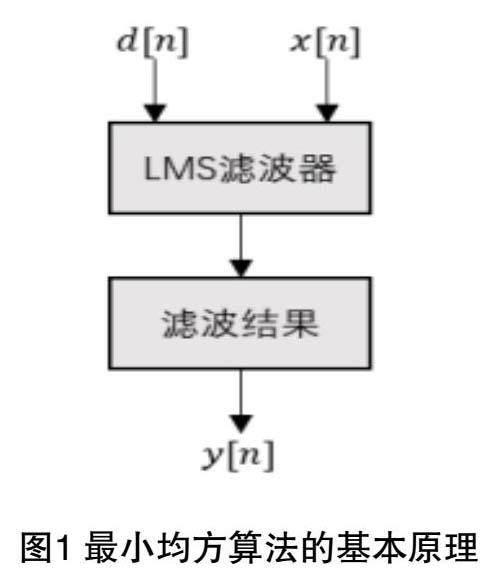
LMS算法的基本思想是不斷地根據當前時刻的誤差信號來調整濾波器的系數，使得誤差信號盡可能地減小。通過這種迭代更新的方式，逐漸使得濾波器收斂到最優解，從而實現了對噪聲的有效抑制和信號的恢復，基本流程如圖1所示。

圖1中，輸入信號x[n]和期望信號d[n]分別作為LMS濾波器的輸入，經過濾波器后得到輸出信號y[n]。然后，通過比較輸出信號與期望信號的差異，計算誤差信號，并根據LMS算法的更新規則調整濾波器的系數，最終實現主動降噪的效果。

LMS算法的特點主要體現在以下幾個方面：首先，LMS算法是一種迭代更新的方法，通過不斷地根據誤差信號調整濾波器的系數，使其收斂到最優解。其次，LMS算法具有簡單易實現、計算量小等優點，適用于實時處理等應用場景。然而，由于其對信號和噪聲的統計特性要求較高，當噪聲為非平穩時，LMS算法的性能就會受到影響，導致收斂速度較慢或者無法收斂[3]。

為了提高LMS算法在非平穩環境下的性能，引入了自適應正則化技術。自適應正則化技術通過引入正則化項，對LMS算法的更新規則進行優化，從而增強了算法的穩定性和收斂速度。具體而言，自適應正則化技術會根據當前的信號和噪聲特性動態調整正則化參數，使其能夠在不同的環境下保持較好的性能表現。

2. 基于正則化的最小均方優化方法

自適應正則化技術能夠有效地克服傳統LMS算法在處理非平穩噪聲時的不足，提高了其在實際應用中的適用性和效果。設濾波器的系數為w[n]，輸出為y[n]，期望信號為d[n]，則LMS算法的更新規則如式2所示。

為了引入自適應正則化，將LMS算法的目標函數定義為：

（3）

其中，表示期望運算符。

然后，引入正則化項R（w），目標函數變為：

（4）

其中，λ是正則化參數。

常見的正則化項包括L2范數正則化和L1范數正則化，這里以L2范數正則化為例。正則化項R（w）可表示為：

（5）

其中，表示L2范數，即歐幾里得范數。

綜合以上公式，得到帶有自適應正則化的LMS算法更新規則為：

（6）

其中，2λw[n]是對應于L2范數正則化項的梯度下降項。通過這種方式，可以在LMS算法的更新規則中引入自適應正則化，優化算法的性能，提高其在非平穩環境下的適應能力。

在優化之前，傳統LMS算法的更新規則只考慮了誤差信號與輸入信號的乘積，未能充分考慮噪聲的統計特性和信號的動態變化，導致在非平穩環境下性能表現不佳。此外，傳統LMS算法的參數（如步長參數）需要手動設置，難以適應不同場景下的變化。經過自適應正則化技術的優化后，LMS算法的性能得到了顯著改善。首先，引入了正則化項后，可以有效地抑制噪聲對濾波器系數的影響，提高了算法的穩定性和魯棒性。正則化參數的引入使得算法能夠自適應地調整濾波器的更新規則，根據當前信號和噪聲的特性動態調整步長和正則化程度，從而加速收斂速度并提高抗噪性能[4-5]。此外，自適應正則化技術還能夠減少對參數的手動設置，提高了算法的自適應能力。

3. 實驗模擬

3.1 數據集與實驗方案

在實驗部分，本文采用NOISEX-92數據集對方法進行了測試。該數據集是用于音頻信號處理領域的一個公認的標準數據集，廣泛用于評估降噪算法的性能和效果。該數據集由美國賓夕法尼亞大學（University of Pennsylvania）的研究人員在1992年創建，旨在提供一組包含不同類型噪聲的音頻信號，以便研究者能夠在實驗中模擬實際場景下的降噪任務。NOISEX-92數據集包含了來自六個不同環境和來源的噪聲樣本，涵蓋了飛機噪聲、城市交通噪聲、人聲等常見的環境噪聲類型[6-7]。這些噪聲樣本以及與之對應的干凈信號也被整理出來，以確保數據的質量和多樣性。本文使用該數據集進行實驗的方法為：

（1）準備實驗環境。在Matlab平臺上創建一個新的工程，確保所有必要的工具箱和函數庫都已安裝和配置。然后，將NOISEX-92數據集導入Matlab環境中，包括噪聲樣本和相應的干凈信號，確保數據格式正確，并進行必要的預處理，包括歸一化處理和數據劃分。

（2）實現基于LMS算法的主動降噪方法。編寫Matlab代碼，實現LMS算法的基本原理和自適應正則化優化方法。包括定義濾波器結構、初始化參數、編寫主動降噪函數等步驟。

（3）實驗設置。根據實驗的具體要求，設置合適的參數，包括步長參數、正則化參數等。另外，需要將數據集劃分為訓練集和測試集，用于模型的訓練和評估。

（4）實驗訓練。利用訓練集對實現的主動降噪算法進行訓練，即調整濾波器的參數，使其適應于當前的噪聲環境和信號特征。在訓練過程中，需要監測算法的收斂情況和誤差變化，以便及時調整參數和優化算法[8]。

（5）實驗評估。利用測試集對訓練好的主動降噪算法進行評估，比較輸出信號與期望信號之間的差異，評估降噪效果和算法性能。常用的評價指標包括信噪比（Signal-to-Noise Ratio，SNR）、均方根誤差（Root Mean Square Error，RMSE）等。

3.2 實驗結果與分析

本文用SNR和RMSE對優化前后的方法進行對比和評估，實驗結果如表1所示.表1中的SNR和RMSE是兩個常用的評價指標，用于評估降噪算法的效果。

從表1中的數據可以看出，在進行了優化后的主動降噪方法中，SNR提高到了18.6 dB，相較于優化前的方法提升了約3.4 dB；同時，RMSE下降到了0.028，相較于優化前的方法降低了0.006。這些數據變化表明，優化后的主動降噪方法在降噪效果和性能上取得了顯著的改善。

首先，信噪比（SNR）的提高意味著優化后的方法能夠更有效地抑制噪聲，并提高信號的質量和清晰度。從實際應用的角度來看，信噪比的增加意味著在同樣的信號強度下，信號與噪聲之間的區分度更高，使得最終的處理結果更加可靠和準確。其次，均方根誤差（RMSE）的降低表明優化后的方法在估計信號與期望信號之間的差異時更加精確，更接近于期望信號的真實情況[9]。這意味著優化后的方法能夠更準確地恢復原始信號，降低了信號失真和信息損失的程度，提高了降噪算法的可靠性和穩定性。

整體來說，通過對實驗結果的分析，可以明顯看出優化后的主動降噪方法相較于優化前具有更優越的性能表現。這一改進不僅提高了信號的質量和清晰度，還增強了算法的穩定性和準確性，為數字音頻信號處理領域的實際應用帶來了顯著的優勢和價值。

4. 結束語

本文研究了數字音頻信號處理中的主動降噪方法，并以最小均方（LMS）算法為基礎，引入了自適應正則化技術進行優化，并采用NOISEX-92數據集對所提出的優化方法進行了實驗驗證，結果表明優化后的方法在信噪比（SNR）和均方根誤差（RMSE）等評價指標上取得了顯著的改善。通過對本文內容實驗的綜合分析可知，自適應正則化技術作為一種優化方法，能夠有效地改善傳統的LMS算法在處理非平穩噪聲時存在的性能不足的問題，能提高其在實際應用中的適用性和效果。本文的研究內容和實驗結果充分證明了自適應正則化技術對于提高LMS算法在數字音頻信號處理中的主動降噪效果具有重要意義。未來的研究可以進一步探索其他優化方法，并結合實際應用場景，進一步提高降噪算法的性能和適用性。

參考文獻：

[1]張毓忠，冷文.數字音頻信號處理器理論及專用電路設計[J].電子測量與儀器學報，1994（04）：54-57，62.

[2]陳東，錢光弟.音頻信號的數字處理及其應用設計[J].電聲技術，2006（02）：22-25.

[3]李偉，汪竹蓉，李曉強，等.數字音頻認證研究綜述[J].計算機科學，2009，36（10）：21-24.

[4]李忠利，鄒會勉，喬冬冬，等.拖拉機駕駛室耳旁噪聲主動降噪控制[J].科學技術與工程，2018，18（33）：30-35.

[5]費艷鋒，曹祖楊，李堅維.關于主動降噪耳機的研究[J].電聲技術，2020，44（05）：38-40，46.

[6]王向陽，牛盼盼.基于音頻統計特性的數字水印嵌入算法[J].自動化學報，2008（08）：1001-1003.

[7]張戌寶.現代助聽器的降噪技術（單麥克風類）和性能（2）[J].聽力學及言語疾病雜志，2014，22（06）：643-645.

[8]徐帆云.基于Matlab的音頻降噪濾波器設計[J].電聲技術，2017，41（02）：28-33.

[9]陳紹用，徐洋，盛曉偉等.基于濾波最小均方算法的簇絨地毯裝備噪聲主動控制[J].紡織學報，2020，41（07）：88-92.