PBL教學模式在高中數學公式教學中的應用

一、問題提出

PBL教學模式是以建構主義為理論基礎，以問題為教學驅動，依托真實生活情境，以小組合作交流為教學載體，以多元評價為教學反思的綜合性教學模式。在該模式下，教師是課堂的引導者，以問題為基礎，圍繞問題的生成、猜想、探究、感悟展開教學，通過引、問、導幫助學生建構知識；學生是學習的主體，通過問題探究、獨立思考、小組討論等方式經歷思、探、悟，從而內化知識。

數學公式教學容易形成“一背二套”“公式加例題”的模式，輕證明重應用、輕理解重記憶。在誘導公式一節中，這種現象尤為突出，過往我們大多將誘導公式僅視為求值化簡的工具，忽視了公式的來龍去脈，導致不少學生無法準確記憶、熟練應用。基于此，本文將嘗試在大單元教學的視域下，探索將PBL教學模式融入誘導公式的課堂教學，激發學生的學習興趣，提高教學的有效性。

二、教學分析

（一）內容解析

本節內容安排在“任意角和弧度制”“三角函數的概念”之后，可以視作三角函數性質的延伸，遵循函數的研究脈絡，從數與形的角度入手分析，體現數學學習的整體性。同時，誘導公式也是三角函數知識的基礎，是描述函數周期性的重要工具，有著承上啟下的作用，為后續學習角的和差倍分、三角函數的圖象與性質等知識打下基礎。本文將著重探討PBL教學模式在第一課時公式教學中的應用。

本節對誘導公式的推導大致可分為兩種思路：對稱與旋轉。但在舊版教材以及新人教B版、湘教版教材中，均提到了可利用已證明的誘導公式，通過三角函數變形推導得新的誘導公式的方法，從代數角度體現公式間的內在聯系。

（二）學情分析

學生在初中階段對銳角三角函數已經有了初步認識，并掌握了任意角和弧度制、三角函數的概念等知識，對集合、函數也有一定的理解。此外，學生也經歷了借助單位圓研究同角三角函數的基本關系的學習過程，積累了一些合作探究的活動經驗，具有一定的問題意識，初步形成了數形結合、轉化與化歸等數學思想，但其自主探究問題的能力不足、思維欠缺嚴謹性，過程中需要教師適時引導、歸納梳理。

（三）教法研究

PBL教學模式倡導教師在教學中創設真實情境以激發學生學習的興趣，發揮其主動性以建構更可靠的知識，促進學生思維發展。選擇從已經學過的三角函數的定義、誘導公式一等知識入手，借助單位圓研究三角函數的方法，再通過具體三角函數值的求解設置認知沖突，力求創設符合學生“最近發展區”的數學情境，使公式的引入流暢自然，符合知識發展的內在規律。

在本章中，單位圓是問題研究的腳手架，而誘導公式本質上是圓的對稱性的解析表示，因此教師在教學過程中應充分滲透數形結合的思想方法。借助單位圓，突出誘導公式的幾何本質；合理使用信息技術，如使用GGB軟件進行動態演示，挖掘角的終邊與點的坐標之間的關系，將抽象問題具體化，便于學生理解和記憶。

在具體實施過程中，PBL教學模式認為問題是學習的起點，也是知識選擇的根本依據，教師要“會問”，從學生現有知識水平出發，引導其建立內在的“已知”與“未知”的聯系。“問題是數學的心臟”，教師可基于教學內容設置梯度合理的問題串以驅動學生主動學習，由淺入深、層層遞進，問題指向明確、表達簡明清晰。同時，PBL教學模式倡導合作性的課堂學習，認為在學生充分發散思維的情況下，加強小組溝通與合作有利于培養其創新精神、促進知識內化。在本節中，教師可在完成公式二的推導之后，引導學生以小組為單位自主完成后續公式探究，并關注學生的課堂生成，合理規劃、適當干預、多元評價，以免探究流于形式。

（四）教學目標

借助單位圓的對稱性，利用定義推導公式二～六。

（五）教學重點

利用圓的對稱性探究公式二～六。

（六）教學難點

發現圓的對稱性與三角函數之間的關系，建立聯系。

三、教學過程

●環節一：創設情境，提出問題

引入：在之前的學習中，我們借助單位圓定義了三角函數，并得到了誘導公式一，認識到了三角函數周而復始的變化規律。再結合單位圓的幾何性質，得到了同角三角函數的基本關系。

現已知sin20°=a，應如何表示sin 380°，sin 200°，sin（-20°），sin160°，sin70°，sin110°等三角函數的值呢？

學生聯系三角函數的定義，在單位圓中畫出角的終邊猜想結果。

師：上述猜想是否正確，需要我們進一步探究求證。我們知道，圓最重要的性質是對稱性，而對稱性（如奇偶性）也是函數的重要性質。那么，我們能否利用圓的對稱性來進一步研究三角函數的對稱性呢？

（設計意圖：回顧舊知，激發學生的學習興趣，為后續過渡到一般抽象的三角函數的探究作鋪墊。）

●環節二：公式探究，深化理解

△探究1：

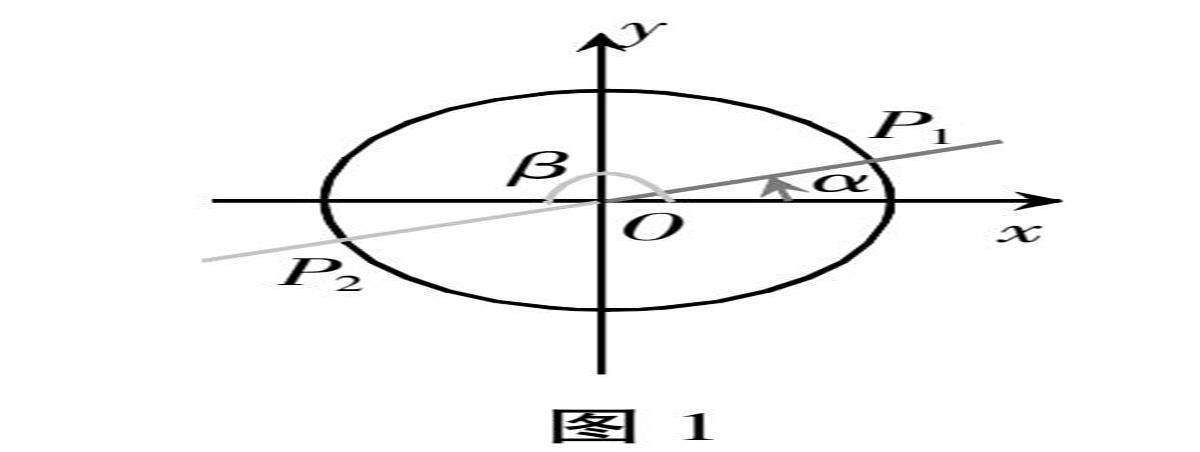
（1）如圖1所示，在直角坐標系內，設任意角α的終邊與單位圓交于點P1。

作P1關于原點的對稱點P2，那么以OP2為終邊的角β與角α有什么關系？

師：P1與P2兩點間的坐標有什么關系？可否由三角函數的定義得到角β與角α的三角函數值之間的關系？

追問1：除了由原點對稱得到外，角（π+α）還可以看成是角α經歷怎樣的變換得到？

追問2：回顧公式二的探究過程，你能簡要概括我們的探究步驟嗎？

學生歸納，教師補充：圓的對稱性—角與角的關系—坐標間的關系—三角函數的關系。

（設計意圖：探究（1）引導學生建立起圓的性質與三角函數的誘導公式之間的聯系。追問1意在引導學生從旋轉的角度認識圓的中心對稱性；追問2意在歸納程序、建立研究方法，為后續類比遷移積累經驗。）

（2）請類比公式二的推導過程，嘗試探究：如過P1作關于x軸（或y軸）的對稱點P3（或P4），那么又可以得到什么結論？

小組合作探究、學生代表展示，師生修改完善，得到公式三、四，歸納公式特征。

追問1：上述推導過程中是否用到了P1所在的位置條件？如果P1在其他象限或者坐標軸上，P1與P3間的坐標關系、P1與P4間的坐標關系會改變嗎？

追問2：公式二～四中的角α的取值范圍是什么？

教師借助GGB軟件進行動態演示，引導學生觀察公式二～四中角α變化時，點坐標間的關系，驗證誘導公式的普適性。

（設計意圖：培養學生善于思考、敢于質疑的科學精神。）

△探究2：

考慮其他的對稱關系，我們是否還能得到一些特殊結論呢？

作P1關于直線y=x的對稱點P1，以OP5為終邊的角γ與角α有什么關系？角γ與角α的三角函數值之間有什么關系？

追問1：關于直線y=x對稱的兩點坐標有什么關系？

追問2：類比公式二～四，可以得到什么結論？

教師提示輔助線，學生結合平面幾何知識完成推導。須說明考慮到α的任意性，關于坐標關系嚴謹的證明將留在后續解析幾何的學習中完成。

△探究3：

以上探究1、探究2中，我們都是對P1作了一次對稱變換，如果再作P5關于y軸的對稱點，又能得到什么結論？

追問1：是否還有其他的變換方式呢？據此你將如何證明公式六？

生1：（軸對稱）角α的終邊首先關于x軸作對稱，再關于直線y=x作對稱。

生2：（旋轉對稱）將角的終邊逆時針旋轉。

追問2：除了利用對稱性，可否利用已有公式推導誘導公式六呢？

教師借助多媒體展示學生具有代表性的推導過程，共同探討完善。

追問3：公式五、六中角α的取值范圍是什么？

（設計意圖：追問1引入旋轉對稱，為后續兩角差的余弦公式的推導作鋪墊；追問2從代數角度體現公式間的內在聯系。）

●環節三：課堂回顧，總結提升

本節我們學習了哪些誘導公式？請你回顧探究過程，思考我們的推導思路是怎樣的，當中蘊含了哪些數學思想方法。

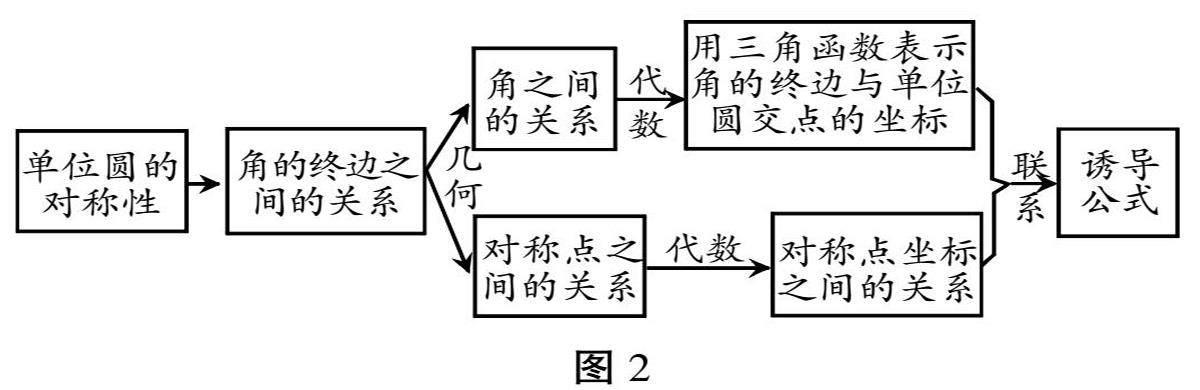
師生共同歸納得出以下思路（見圖2）：

師：本節課，我們通過類比同角三角函數的基本關系的研究方法，借助單位圓的對稱性推導得到誘導公式，由單個公式的學習過渡到公式串的學習，體現了數學思維的一致性和連貫性。值得關注的是，三角函數是以角為變量的特殊的函數，其內容框架和探究路徑與我們之前探究的其他函數相似，當前學習的6組誘導公式都反映了三角函數的性質，也是后續探究三角函數圖象與性質的基礎。而由平面幾何的知識可知，圓最重要的性質是旋轉對稱性，其中又蘊含著三角函數哪些重要的性質呢？待我們后續進一步探究。

（設計意圖：從大單元教學的視域下再次認識誘導公式，有利于學生構建知識體系。）

●環節四：課后訓練，反思內化

1.結合單位圓完成本節內容的思維導圖。

2.嘗試推導圓的正切。

3.完成本節課后習題。

四、教學反思

高中數學課堂教學中蘊含著“濃縮在教材中的數學家思維、對教材進行再加工的教師思維、被教材和教師引導著的學生思維”三種思維活動，數學教學就是這三種思維相互碰撞和交融的過程。PBL教學模式應用于公式教學，一方面有利于促進教師深入整合教材、設計教學環節，讓數學家思維更為自然地與學生思維對接；另一方面，以問題為驅動力，創設情境、合作探究、拓展延伸、反饋評價等教學環節，有利于加深學生對問題的思考與知識的建構，提升其解決問題的能力。值得注意的是，當前PBL教學模式應用于高中數學課堂教學還面臨一些困境，如課堂活動設計不合理、學生探究合作不夠深入、評價較為單一等，這需要廣大教師不斷實踐探索、思考交流、沉淀經驗。

（作者單位：福建省廈門集美中學）

編輯：曾彥慧

注：本文系廈門市第六批基礎教育課程改革課題（Z643）的研究成果。

作者簡介：余奕（1994—），女，漢族，福建廈門人，理學學士，中學一級教師，研究方向：高中數學教育。