解決含參數不等式恒成立問題和函數零點討論問題的兩種方法

馬大文

［摘 要］對于含參數不等式恒成立問題和函數零點討論問題，普通高中的學生常常束手無策。文章結合例題歸納解決含參數不等式恒成立問題和函數零點討論問題的兩種方法——定點旋轉直線法和平移直線法，旨在為普通高中學生提供方法依據，幫助他們破解難點。

［關鍵詞］含參數不等式恒成立問題；函數零點討論問題；定點旋轉直線法；平移直線法

［中圖分類號］??? G633.6??????? ［文獻標識碼］??? A??????? ［文章編號］??? 1674-6058（2024）14-0027-03

歷年廣西普通高中學業水平考試數學試卷的壓軸題，都是利用導數求切線方程、求函數單調區間，以及討論含參數不等式恒成立、函數零點個數等問題。其中，含參數不等式恒成立問題和函數零點個數討論問題在大多數情況下可以用兩種直線法解決，一是定點旋轉直線法，二是平移直線法。這兩種直線法不僅對學業水平考試的備考有很好的作用，還對高考備考有一定的啟發和幫助。

一、方法引入

現以2021年廣西普通高中學業水平考試數學試題第38題為例歸納定點旋轉直線法和平移直線法。

［例1］已知函數[f（x）=alnx+bx]，曲線[y=f（x）]在點[（1，f（1））]處的切線方程為[3x-y-1=0]。

（1）求[f（x）]的解析式；

（2）設[g（x）=x2+mx-f（x）]，試討論函數[g（x）]的零點的個數。

解：（1）∵[f '（x）=ax+b]，∴[f '（1）=a+b]，∵[f（1）=aln1+b=b]，[∴]切點坐標為（1，[b]），

由點斜式得切線方程：[y-b=f '（1）（x-1）]，即[（a+b）x-y-a=0]，∵已知切線方程也表示為[3x-y-1=0]，[∴a+b=3，-a=-1，]即[a=1，b=2，][∴f（x）=lnx+2x]。

（2）∵[g（x）=x2+mx-f（x）]，∴[g（x）=x2+mx-lnx-2x]，若函數[g（x）]有零點，則[g（x）=0]，即[x2+mx-lnx-2x=0（x>0）]。

方法一：變式為[（m-2）x=lnx-x2]，令[y=（m-2）x]和[G（x）=lnx-x2]，則[G'（x）=1x-2x=-2x+22x-22x]。

當[x∈0，22]時，[G'（x）>0]，[G（x）]為增函數；當[x∈22，+∞]時，[G'（x）<0]，[G（x）]為減函數。故[G（x）]在[x=22]處有最大值，即[G（x）max=G22=-ln2+12]。當[x→0]時，[G（x）=lnx-x2→-∞]；當[x→+∞]時，由洛必達法則知，[limx→+∞lnxx2=limx→+∞（lnx）′（x2）′=limx→+∞1x2x=limx→+∞12x2=0]，即[x2]變大的速度比[lnx]變大的速度快，所以[G（x）=lnx-x2→-∞]。

（此處也可以對[y=lnx]和[y=x2]的圖象進行比對，判斷[G（x）]的變化趨勢）

則[G（x）]的大致圖象如圖1所示，設過點（0，0）的直線[y=（m-2）x]與曲線[G（x）=lnx-x2]相切的切點為[（x0，lnx0-x20）]，則切線斜率滿足[G'（x0）=（lnx0-x20）-0x0-0=1x0-2x0]，即[x20+lnx0-1=0]，解得[x0=1]，故切線斜率[k0=1x0-2x0=-1]。當[m-2>-1]時，即[m>1]時，直線[y=（m-2）x]與曲線[G（x）=lnx-x2]無公共點，即[g（x）]沒有零點；當[m-2=-1]時，即[m=1]時，直線[y=（m-2）x]與曲線[G（x）=lnx-x2]有1個公共點，即[g（x）]有1個零點；當[m-2<-1]時，即[m<1]時，直線[y=（m-2）x]與曲線[G（x）=lnx-x2]有2個公共點，即[g（x）]有2個零點。

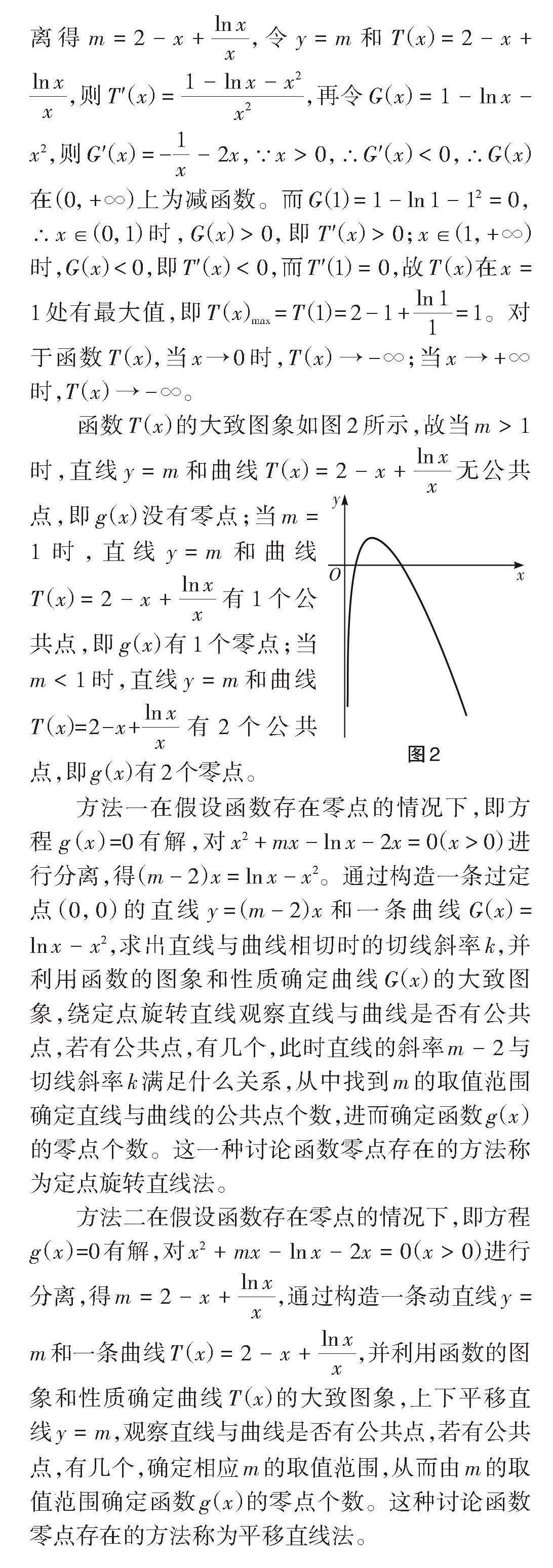
方法二：由[x2+mx-lnx-2x=0（x>0）]，分離得[m=2-x+lnxx]，令[y=m]和[T（x）=2-x+lnxx]，則[T'（x）=1-lnx-x2x2]，再令[G（x）=1-lnx-x2]，則[G'（x）=-1x-2x]，∵[x>0]，∴[G'（x）<0]，∴[G（x）]在[（0，+∞）]上為減函數。而[G（1）=1-ln1-12=0]，∴[x∈（0，1）]時，[G（x）>0]，即[T'（x）>0]；[x∈（1，+∞）]時，[G（x）<0]，即[T'（x）<0]，而[T'（1）=0]，故[T（x）]在[x=1]處有最大值，即[T（x）max=T（1）=2-1+ln11=1]。對于函數[T（x）]，當[x→0]時，[T（x）→-∞]；當[x→+∞]時，[T（x）→-∞]。

函數[T（x）]的大致圖象如圖2所示，故當[m>1]時，直線[y=m]和曲線[T（x）=2-x+lnxx]無公共點，即[g（x）]沒有零點；當[m=1]時，直線[y=m]和曲線[T（x）=2-x+lnxx]有1個公共點，即[g（x）]有1個零點；當[m<1]時，直線[y=m]和曲線[T（x）=2-x+lnxx]有2個公共點，即[g（x）]有2個零點。

方法一在假設函數存在零點的情況下，即方程g（x）=0有解，對[x2+mx-lnx-2x=0（x>0）]進行分離，得[（m-2）x=lnx-x2]。通過構造一條過定點（0，0）的直線[y=（m-2）x]和一條曲線[G（x）=lnx-x2]，求出直線與曲線相切時的切線斜率[k]，并利用函數的圖象和性質確定曲線[G（x）]的大致圖象，繞定點旋轉直線觀察直線與曲線是否有公共點，若有公共點，有幾個，此時直線的斜率[m-2]與切線斜率[k]滿足什么關系，從中找到[m]的取值范圍確定直線與曲線的公共點個數，進而確定函數g（x）的零點個數。這一種討論函數零點存在的方法稱為定點旋轉直線法。

方法二在假設函數存在零點的情況下，即方程g（x）=0有解，對[x2+mx-lnx-2x=0（x>0）]進行分離，得[m=2-x+lnxx]，通過構造一條動直線[y=m]和一條曲線[T（x）=2-x+lnxx]，并利用函數的圖象和性質確定曲線[T（x）]的大致圖象，上下平移直線[y=m]，觀察直線與曲線是否有公共點，若有公共點，有幾個，確定相應[m]的取值范圍，從而由[m]的取值范圍確定函數g（x）的零點個數。這種討論函數零點存在的方法稱為平移直線法。

定點旋轉直線法和平移直線法都是在假設某函數g（x）存在零點的情況下，由[g（x）=0]分離出一條直線和一條曲線，通過直線的旋轉或平移，觀察參數變化范圍，確定直線與曲線的公共點個數，從而確定函數的零點個數。定點旋轉直線法和平移直線法雖然都有一條直線，但定點旋轉直線法中的直線是過定點的，是繞定點旋轉的動直線；而平移直線法中的直線不過定點，是一條和[y]軸垂直的動直線。

在解決問題的過程中，如果能分離出一次函數型的，可以考慮用定點旋轉直線法求解與證明；如果不能分離，一般考慮用平移直線法。具體用哪種方法，應根據問題的條件具體分析。

二、定點旋轉直線法和平移直線法的解題步驟

設函數[y=f（x）]，且[f（x）]有零點，即有[f（x）=0]。

（一）定點旋轉直線法

1.分離過定點[P（x0，y0）]的動直線[l：y=k（x-x0）+y0]和曲線C：[y=T（x）]。

2.利用函數的圖象和性質畫出[y=T（x）]的大致圖象。

3.設直線與曲線的切點坐標為[（a，T（a））]，利用導數的幾何意義和斜率的坐標計算公式，即由[T'（a）=y0-T（a）x0-a]求出[a]，進而求出切線斜率[k0=T'（a）]。

4.旋轉動直線[l]，當直線[l]與曲線C沒有公共點時，即[y=f（x）]沒有零點時，確定[k]與[k0]的關系；當當直線[l]與曲線[C]有公共點時，即[y=f（x）]有零點時，確定[k]與[k0]的關系。

（二）平移直線法

1.分離動直線[l：y=m]和曲線[C]：[y=T（x）]。

2.利用函數的圖象和性質畫出[y=T（x）]的大致圖象。

3.平移動直線[l]，當直線[l]與曲線[C]沒有公共點時，即[y=f（x）]沒有零點時，確定[m]的取值范圍；當直線[l]與曲線C有公共點時，即[y=f（x）]有零點時，確定[m]的取值范圍。這里[m]的取值范圍與函數[y=T（x）]的值域有關，特別是函數的最值與極值和端點與斷點有密切關系。

在定點旋轉直線法和平移直線法的應用中，在畫[y=T（x）]的大致圖象時，一般由定義域和值域確定圖象的范圍，由單調性、最值點、極值點、端點和斷點、奇偶性、對稱性和周期性、函數的變化趨勢等確定圖象的大體形狀。

三、兩種直線法在不同場景下的應用

（一）平移直線法的應用

［例2］已知函數[f（x）=x2+x-alnx-2]。若[x>1]時，[ f（x）>0]恒成立，求實數[a]的取值范圍。

解：∵[f（x）>0]恒成立，即[x2+x-alnx-2>0]，有[alnx1]，∴[lnx>0]，分離得[a0]。∴[M（x）]在（1，+∞）上是增函數，∴[M（x）>M（1）=0]，∴[G'（x）>0]，∴[G（x）]在（1，+∞）上是增函數，∴[G（x）>G（1）=0]，∴[T'（x）>0]，∴[T（x）]在（1，+∞）上是增函數，∴[T（x）>limx→1T（x）=] [limx→1x2+x-2lnx=limx→1（x2+x+2）′（lnx）′=limx→12x+11x=limx→1（2x2+x）=3]。

則[T（x）]的大致圖象如圖3所示，當直線[y=a]在過界點（1，3）的直線[y=3]位置或以下時，不等式恒成立，此時[a]的取值范圍是[-∞，3]。

（二）定點旋轉直線法的應用

［例3］已知函數[f（x）=ax2]，[g（x）=xlnx]。若[f（x）≥g（x）]恒成立，求實數[a]的取值范圍。

解：∵[x>0]， [f（x）≥g（x）]恒成立，即[ax2≥xlnx]可變形為[ax≥lnx]，令[y=ax]和[T（x）=lnx]，則[T'（x）=1x]。設過定點（0，0）的直線[y=ax]與曲線[T（x）=lnx]相切的切點為[（x0，lnx0）]，則切線斜率滿足[T'（x0）=lnx0-0x0-0=1x0]，即[lnx0=1]，解得[x0=e]，故切線斜率[k0=1x0=1e]。而[T（x）=lnx]的大致圖象如圖4所示，故當[a≥k0]時，即[a≥1e]時，不等式恒成立，此時實數[a]的取值范圍是[1e，+∞]。

［例4］已知函數[f（x）=ax-lnx（a∈R）]。若[g（x）=f（x）+1-1xlnx]的圖象與直線[y=a]相切，求[a]的值。

解：由[g（x）=f（x）+1-1xlnx]，得[g（x）=ax-1xlnx]，[∵]直線[y=a]與曲線[g（x）=ax-1xlnx]相切，∴[a=ax-1xlnx]有唯一解，分離變量得[a（x-1）=lnxx]。令[y=a（x-1）]和[T（x）=lnxx]，則[T'（x）=1-lnxx2]，當[x∈（0，e）]時，[T'（x）>0]，[T（x）]為增函數；當[x∈（e，+∞）]時，[T'（x）<0]，[T（x）]為減函數，∴[T（x）]存在最大值，即[T（x）max=T（e）=1e]。當[x→0]時，[lnx→-∞]，[1x→+∞]，∴[lnxx→-∞]；當[x→+∞]時，[lnxx>0]，又∵[limx→+∞lnxx=limx→+∞（lnx）'x'=limx→+∞1x=0]，則[T（x）]的大致圖象如圖5所示，設過定點（1，0）的動直線[y=a（x-1）]與曲線[T（x）=lnxx]相切的切點為[x0，lnx0x0]，則切線斜率滿足[T'（x0）=1-lnx0x02=lnx0x0-0x0-1]。整理得[x0+lnx0-2x0lnx0-1=0]，可知[x0=1]是方程的解，故切線斜率[k0=T'（x0）=1-lnx0x02=]1；[∴] [a=k0=1]時，[y=a（x-1）]與曲線[T（x）=lnxx]相切，也就是[a=1]時，曲線[g（x）]與直線[y=a]相切。

四、兩種直線法的使用說明

普通高中學生的邏輯推理能力相對較弱，如果他們按照常規的解題思路和方法解答導函數問題，難度很大，較難得分。定點旋轉直線法和平移直線法的解題雖然不是最簡潔的，但它們可以按照一定的程序步驟走，可給學生創造拿分的機會，增強他們解題的勇氣和信心。應用定點旋轉直線法和平移直線法的難點在于勾畫出曲線的形狀和判斷圖形的變化趨勢。對此，教師可引導學生借助幾何畫板研究、辨析不同函數的圖形，以及讓學生借助高等數學中的洛必達法則判斷圖形的變化趨勢。

（責任編輯??? 黃春香）