以問題為導向,促進深度學習
【摘要】課堂問題是數學課堂教學的重要手段,它在激發學生學習動機、引導學生深度思考、培養學生高階思維等方面發揮著重要作用.課堂提問為學生提供了獨立思考和合作交流的機會,為開展深度教學提供了前提.在課堂教學中,教師應結合教學實際精心設計問題,讓學生在問題的探索中領悟數學本質、積累數學活動經驗、提升數學素養.
【關鍵詞】課堂提問;深度教學;數學素養
在傳統課堂教學中,部分教師認為提高學生學習能力、培養學生數學思維能力的捷徑就是“多講多練”.然而“多講多練”易使思維固化,不利于學生的長遠發展.為改變這一局面,教師應創設有意義的教學情境,提出有價值的“課堂問題”,以此在問題的驅動下促進深度學習,培養學生勤于思考的習慣,提升學生的綜合素養[1].筆者在教學“圖形的旋轉”時,圍繞旋轉的本質特點精心設計課堂問題,讓學生在問題的探索中挖掘知識本質,發展學生核心素養.
1 教學分析
旋轉是繼平移、軸對稱之后的又一圖形運動.學生通過前面兩種圖形運動的學習,已經有了一定的變換思想,加之初中生具有一定的觀察、分析、抽象能力,這為“生本”課堂的開展提供了便利.在教學中可以從學生已有的知識、經驗出發,引導學生運用類比方法來探究旋轉,這樣從學生熟悉的內容出發不僅可以鞏固探究方法、強化認識,而且可以降低學習的難度,激發學生對數學探究的興趣,同時通過有效的類比可以將三種運動有機地結合在一起,讓學生深刻地體會三者之間的異同.不過,雖然類比設計好處很多,但是難免會缺少一些創新和內涵.在本課教學中,教師圍繞“旋轉”這一本質屬性設計核心問題,讓學生在問題的引領下去發現、去探索,逐漸揭開“旋轉”的神秘面紗.
2 教學簡錄
2.1 認識旋轉
師 你們能列舉一些生活中有關旋轉的例子嗎?
生1 摩天輪、風車.
生2 轉動的風扇.
生3 地球自轉、公轉.
……
師 非常好,那么你們能在網格紙上畫一些旋轉的圖形嗎?教師預留時間讓同學們動手畫圖,并與同桌進行互動交流.
師 結合旋轉實例及創作成果,你能用語言來描述它們的運動過程嗎?(學生積極思考)
生4 圍繞一個點轉動.
生5 圍繞一個點轉動一定角度.(生補充道)
師 還有其他不同意見嗎?
設計意圖 引導學生從生活實際出發,通過感知生活中的旋轉,逐漸抽象旋轉的定義.這樣在師生、生生的互動交流中,抽象的概念變得更加生動、形象,更易于學生理解和接受,使課教學更堂生動、活躍.
2.2 探究旋轉
師 這里有個旋轉,結合視頻說一說它的運動過程.(教師投影展示三角形繞某點旋轉的視頻)
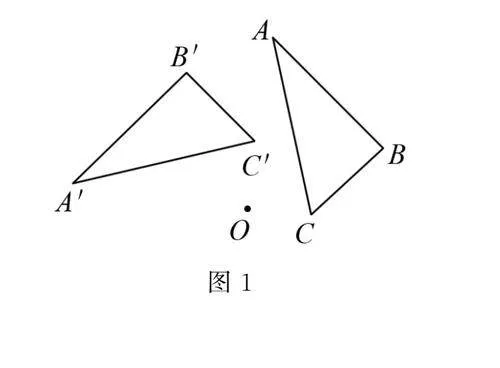
生1 如圖1,△ABC繞點O逆時針旋轉90°得到△A′B′C′.
師 很好,它是否滿足旋轉的定義呢?
生齊聲答 滿足.
師 觀察圖1,說一說旋轉前后哪些量不變?
生2 旋轉前后,△ABC的形狀沒有發生改變,它與△A′B′C′全等.
師 很好,那么除了看到△ABC在旋轉以外,還有其他變換嗎?(學生沉思)
生3 線和點也在作同樣的旋轉.
生4 圖形和線是有無數個點組成的,所以當圖形轉動時,點也在轉動.
師 大家說得非常好,分析得非常透徹.現在我們從點的角度思考,你能發現怎么樣的結論呢?
師 圖形中有無數個點,大家在思考問題時可以從某一個具體的點出發,看看通過這個具體的點的運動過程,你能得到什么結論?猜想那些無法具象的點會怎樣變化呢?
以上問題具有一定的開放性,教師預留充足的時間讓學生思考、交流,教師采集素材展示.
生5 點A繞著點O逆時針旋轉90°到A′,點B繞著點O逆時針旋轉90°到B′,其他點亦是如此.
生6 ∠AOA′=90°,OA=OA′;∠BOB′=90°,OB=OB′;∠COC′=90°,OC=OC′.其他對應點亦是如此,因為它們繞O點轉動,所以O點到它的距離相等.
師 非常好的發現,你能進一步總結一下嗎?
生7 旋轉前的點與旋轉后的點到O的距離相等,它們形成的以O為頂點的角的度數均為旋轉角.
師 還有嗎?(生表示沒有其他發現了)
師 比如由OA=OA′相等,你能夠得到什么結論呢?(教師及時提示,引導學生進一步探究)
生9 連接AA′,在△AA′O中,OA=OA′,點O在AA′的垂直平分線上.
師 很好,通過研究點的旋轉我們發現了這么多結論.現在再看圖形,此時可以怎樣理解旋轉呢?
生10 在圖形旋轉時,與圖形相關的所有元素也發生著同樣的變化.而圖形是由點組成的,所以其本質是點的運動.點怎么動,圖形就怎么動;反之,圖形怎么動,點也怎么動.
師 在之前我們也有過類似的經驗,課后大家不妨將這三種運動進行類比,看看你有哪些收獲.
設計意圖 在教學中,教師引導學生思考圖形變換與點變換之間的關系,引導學生通過對點的運動變化來刻畫圖形的變化,凸顯數學本質.在教學中,教師將類比學習的機會交給學生,讓學生將新、舊知識串聯起來,通過類比明晰三種運動的區別與聯系,進而將新知納入到原有認知體系中去,培養學生的自主學習能力[2].
3 結語
在本課內容學習前,學生已經有了平移、軸對稱的學習經驗,為此在具體教學中大多教師會運用類比思想展開教學.雖然通過類比學生也能很好地理解相關的概念,但是直接運用類比,似乎缺少一些新意,難以凸顯問題的本質.另外,初中生已經具備了一定的類比分析能力,為此教師可以將類比學習的機會交給學生,這樣既可以提高學生的自主學習能力,又可以讓學生通過進一步探究深化對知識的理解.
總之,教師應以學生發展為目標設計教學活動,引導學生通過思考、探索、交流等方式揭示數學本質,進而提高學生學習能力,發展學生基本素養.
參考文獻:
[1]陳柏良.構建深度學習的數學課堂[J].中學數學教學參考,2017(11):14-17.
[2]祝艷.教學之“法”,貴在“以生為本”——核心素養視角下對初中數學教學的思索[J].數學教學通訊,2019(2):35-36.
[3]李勇.類比思想在初中數學中的應用研究[J].中學數學(初中版),2020(9):27-28.

