基于改進集合經驗模態分解的信號處理方法研究趙斯琪

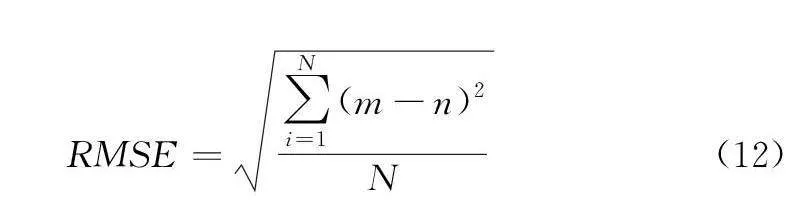
關鍵詞：信號處理;EEMD;PCA

中圖分類號：TP391.9 文獻標志碼：A

0 引言（Introduction）

信號處理采集過程中不可避免地會受到噪聲的干擾。由于檢測信號具有非線性、非平穩特征[1]，因此只有對采集到的缺陷信號進行處理，才能準確地獲得超聲缺陷信號的特征，進而順利地完成檢測任務。

王萍[2]通過EEMD對水聲信號進行處理，較好地提取了信號特征，可以作為水聲信號識別的一種補充手段。陳笑穎等[3]通過EEMD發現對車輛動態稱重信號具有較好的去噪效果，可提高系統測量的精度與準確性。

PCA 是一種多元分析方法，能夠非監督地降維消噪。WU[4]對滾動軸承故障診斷進行研究，使用PCA算法對故障特征進行降維，能夠有效地識別不同的故障狀態。

本文采用EEMD結合PCA算法對超聲信號進行處理，能優化EEMD算法分解出的信號分量特征數不足帶來的誤差，與單一EEMD對比，本文算法更適用于處理超聲信號。

1 算法原理（Algorithm principle）

1.1EEMD理論

EEMD是一種將具有頻率均勻分布特性的高斯白噪聲添加到經驗模態進行分解（Empirical Mode Decomposition，EMD）的方法。

EMD方法突破了常規信號處理方法的瓶頸，能夠自適應分解信號分量，EEMD方法也繼承了這一優點，通過在原始信號上添加高斯白噪聲作為補充信號尺度，使得各個尺度的信號會自動映射到與背景白噪聲相關的適當尺度上，改變了極值點間隔，從而使信號均勻地分布在整個頻帶上，補充了丟失的信號尺度，并確保每次計算時，能夠準確獲取信號上下包絡線的局部均值，從而避免模態混疊現象。添加大量的白噪聲后，通過在最終分解結果中取均值，可以抵消添加的噪聲，唯一穩定保留的就是信號本身。EEMD方法可以自適應地分解固有模態函數（Intrinsic Mode Function，IMF），并按照頻率降序排列依次展開，通過頻譜可得，高頻部分主要是噪聲，低頻部分是有效信號。在處理信號時，通過重構有效IMF分量去除噪聲和剩余分量，就可以得到沒有模態混疊現象的信號。

（3）分別對K 組xK （t）進行EMD分解，得到K 組IMF分量。

（4）將“步驟（3）”中得到的K 組IMF分量進行簡單的總體平均計算，最終得到一組IMF分量。

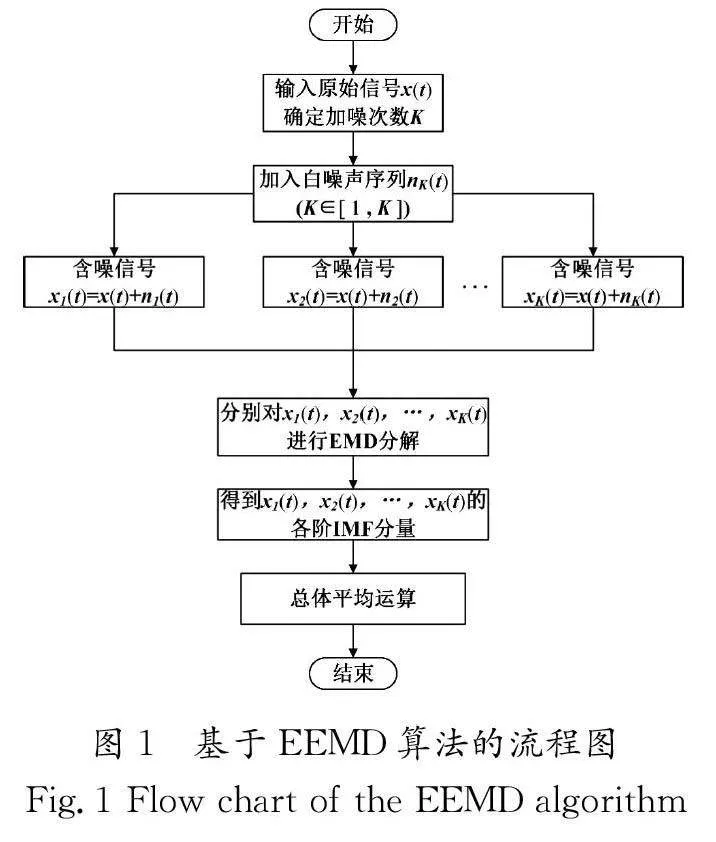
基于EEMD算法的流程圖如圖1所示。

在EEMD分解信號時，若A 值過小，則白噪聲不能使每個分量尺度均勻分布且分量的主頻率唯一，很難消除信號中斷和抑制模態混疊;若A 值過大，則會造成較大的噪聲干擾，在集合平均時，不能完全消除添加的白噪聲，進而影響最后分解的結果。

由于EEMD的分解對噪聲比較敏感，所以A 值通常比較小。當K 值不斷增大時，所添加高斯白噪聲對分解結果的影響可以減小至忽略不計。在添加相同A 值的高斯白噪聲時，K值較小，在平均運算中不能消除添加白噪聲對IMF分量的干擾;當K 值不斷增大時，添加的白噪聲對分解結果的影響逐漸減小，分解效果得到了提升。當K 值過大時，分解信號計算量增大，導致信號分解效率降低。通常，K 值設置為幾百次。

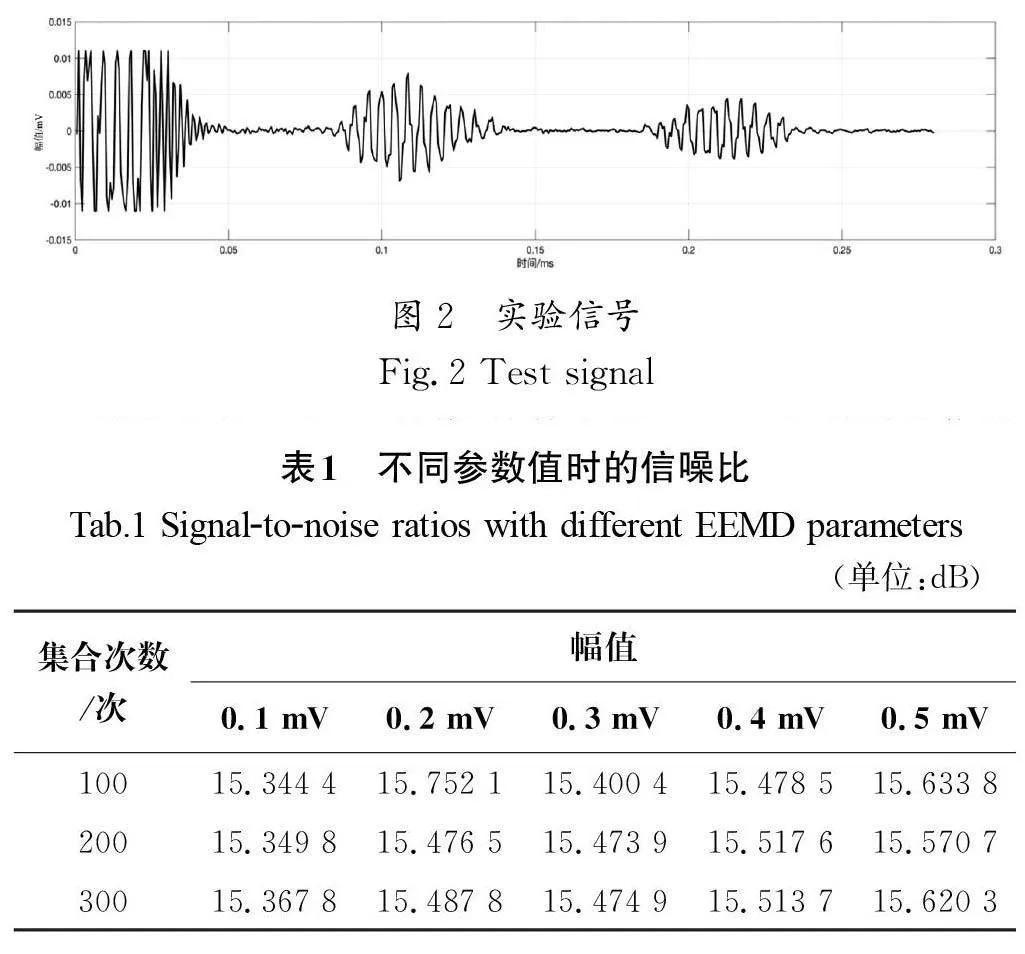
本文通過一個實際的超聲信號進行實驗，實驗信號是電磁超聲換能器在1 mm 厚的鋁板上激發的蘭姆波，激發頻率為657 kHz，實驗信號如圖2所示。

通過改變A 和K 的值，計算出經EEMD處理后的信噪比，進而選取適合的參數，具體數值如表1所示。

對比表1中的數據發現，添加幅值為0.2 mV、集合平均次數為100次時，所得信噪比為最大值，并且當集合平均次數不斷增大時，對應的信噪比數值逐漸趨于穩定，說明過量地增加集合次數對分解結果的影響不大。

綜上，本文選用白噪聲幅值為0.2 mV、集合平均次數為100次作為EEMD的參數。

1.2PCA理論

PCA算法的基本思想是將原來相關的一系列原始數據進行重新組合，轉換為彼此之間互不相關的一系列數據，這些互不相關的數據就是原始數據的線性組合，并且用新的數據可以最大限度地反映原始數據的主要信息，避免數據信息的冗余現象出現。PCA算法步驟如下。

通過相關系數法可以篩選出與原始信號相關程度高的信號分量，找到分界點后，過濾掉相關程度低的分量，保留相關程度高的分量，進而更好地保留原始信號中的缺陷信號特征。

2 改進方法（Improvement method）

EEMD方法在處理超聲無損檢測信號時，雖然能消除模態混疊、完成去噪，但是本質上是改善后的多次EMD分解。與傳統的EMD分解相比，計算量顯著增加，要保證信號處理的精度，必須提高信號處理的效率。此外，EEMD算法分解出的IMF分量會按照頻率的高低依次展開，但噪聲是一種頻率較高的信號。EEMD算法在重構信號時，直接剔除了高頻低階的含噪IMF和殘留分量，但是不能保證高頻分量中不含有有效信號成分，從而造成部分缺陷信號丟失后的誤差，影響后續分析結果。在處理超聲無損檢測信號時，需要盡可能地保留IMF 分量中的有效信號。

本文提出一種將PCA算法引入EEMD中的算法，在處理EEMD分解出的以特征信號為主的IMF分量時，能使信號中的缺陷特征得以最大限度地保留。對原始信號先進行EEMD 分解后，再進行PCA保留缺陷信號處理。

通過EEMD分解出的各個IMF分量與原信號之間的相關系數，判斷該分量是否以缺陷信號為主，對以缺陷信號為主的IMF分量分別進行PCA處理，將經過處理的所有分量進行重構得到最后的缺陷信號。具體算法過程如下。

（1）使用EEMD 算法對原始信號進行分解，得到IMF 分量。

（2）采用相關系數法將IMF分量分為以噪聲為主的IMF 分量和以缺陷信號為主的IMF分量。

（3）對以噪聲為主的IMF分量直接舍去，對以缺陷信號為主的低頻IMF分量進行PCA處理。

（4）將處理的后IMF分量進行重構，得到重構信號。

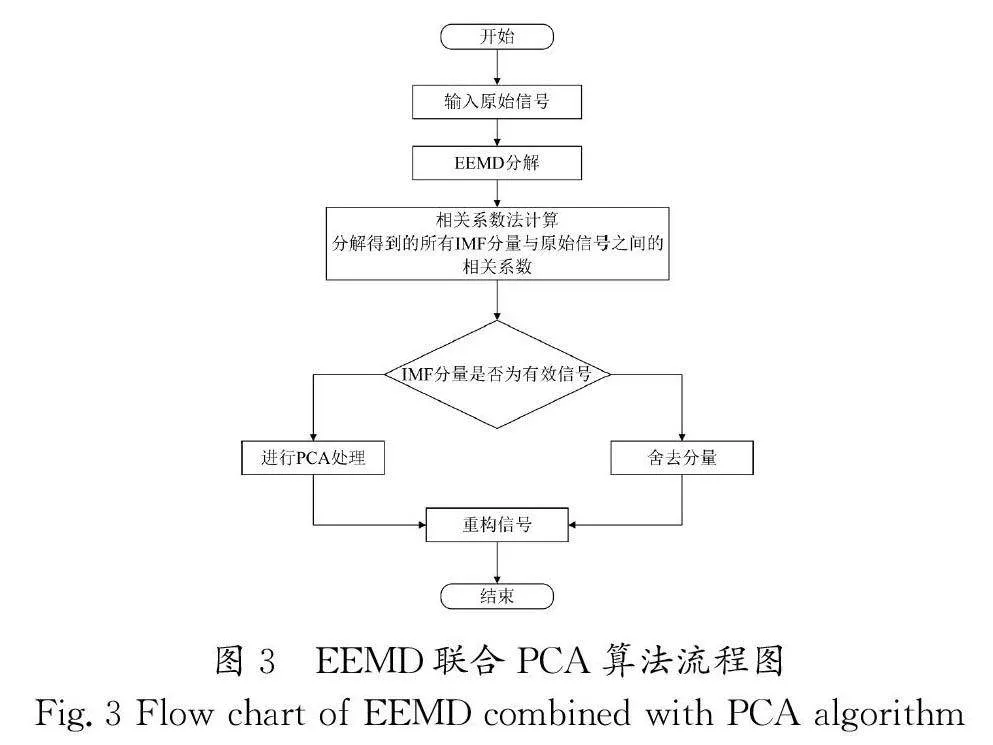
EEMD聯合PCA算法的流程圖如圖3所示。

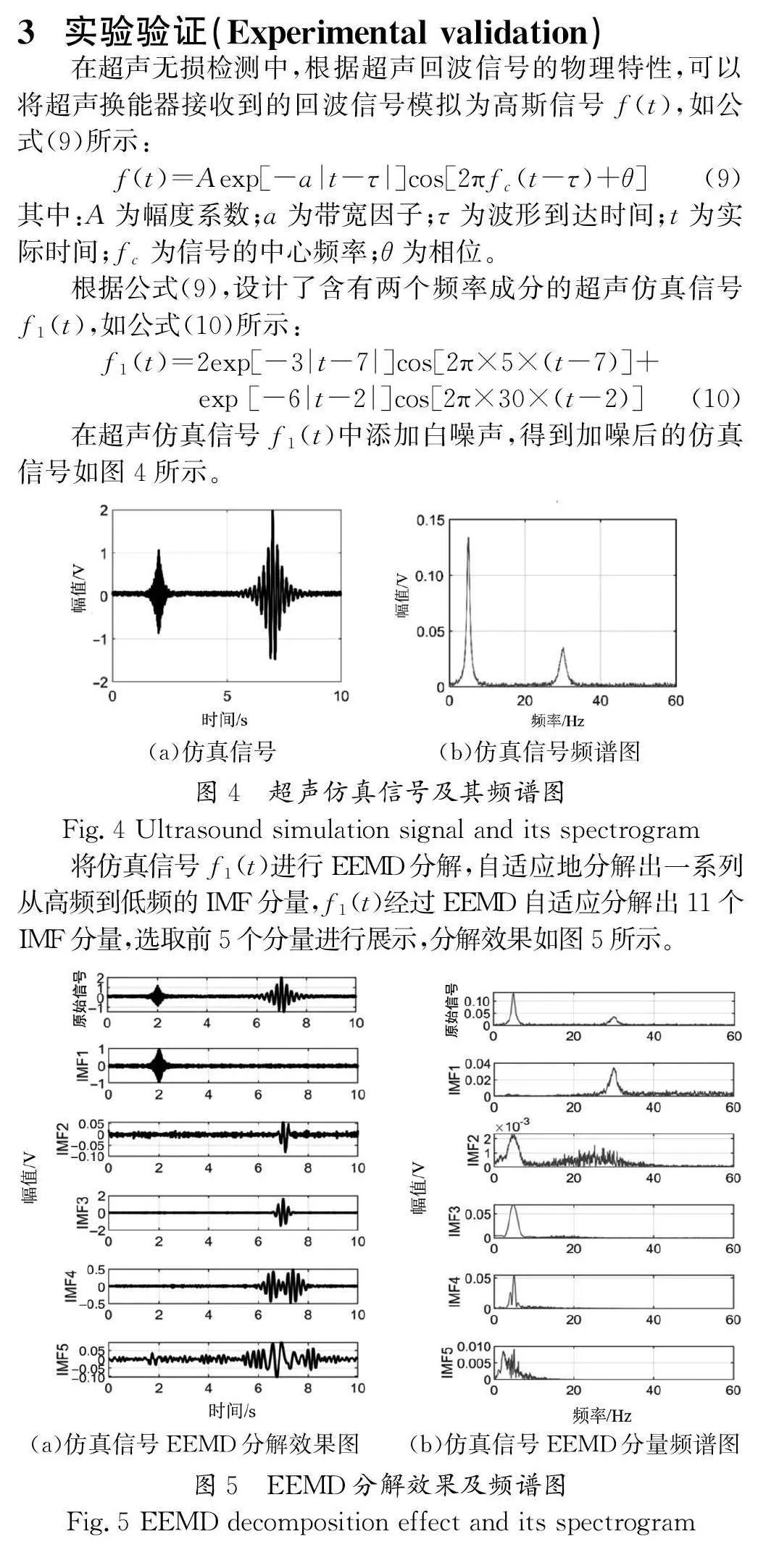
計算各IMF分量和仿真信號f（t）之間的相關系數，選取前5個IMF分量，具體數值如表2所示。

根據表2中的數據，原始信號被自適應地分解成多個IMF 分量，并且這些分量存在“低-高-低”的特征，IMF分量與原始信號的相關系數的第一個極大值點是imf，即imf 是高頻噪聲IMF分量和低頻特征IMF分量的分界點。將imf 和imf分量舍去，對剩余分量進行PCA算法的處理，最后對IMF分量進行重構。

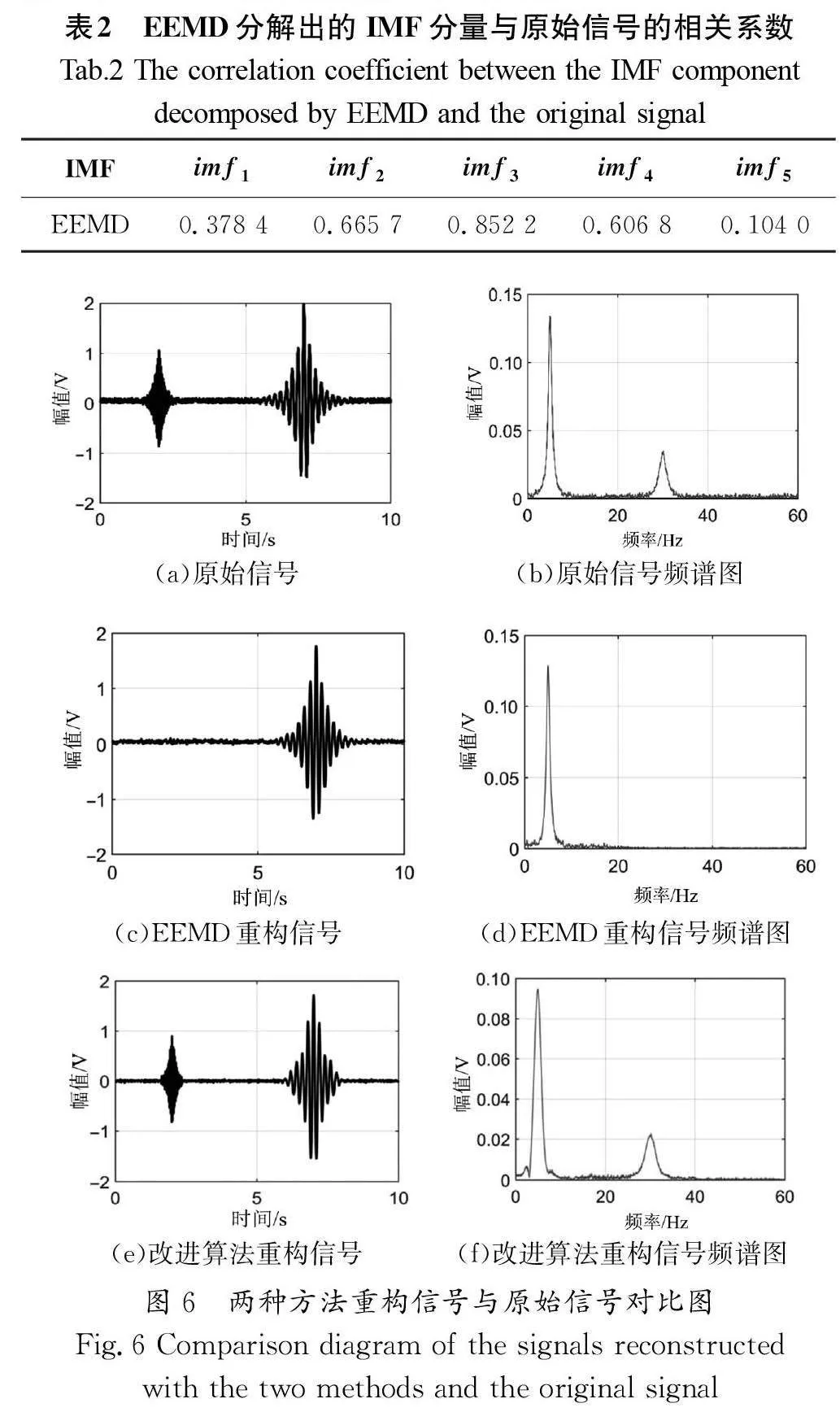
EEMD算法重構信號如圖6（c）所示，基于改進后的EEMD聯合PCA算法重構信號如圖6（e）所示。

從圖6（b）可以看出，原始信號中主要的頻率有兩個。在圖6（d）中，當采用EEMD算法處理仿真信號時，信號中的高頻信號被去除，只保留了低頻信號，處理結果誤差較大。當采用改進后的EEMD聯合PCA算法處理仿真信號時，重構信號的低頻部分被找回，噪聲也有所改善[圖6（f）]。因此，改進后的算法相比于單一EEMD處理方法，在降噪的同時，還能夠保留更多的有效信號。

采用信噪比、均方根誤差評價處理效果，信噪比（Signal-Noise Ratio，SNR）的計算如公式（11）所示：

SNR=20×log（norm（n）/norm（m-n）） （11）

其中：m 為含噪信號;n 為純凈信號;norm為求范數。

均方根誤差（Root Mean Squared Error，RMSE）的計算如公式（12）所示：

其中：m 為含噪信號，n 為純凈信號，N 為信號采樣點數[8]。

采用公式（11）和公式（12）計算處理后的效果比較如表3 所示。

經計算，當采用EEMD聯合PCA算法進行信號重構時，重構信號的信噪比為29.523 7 dB，相較于單一EEMD方法的信噪比提高了51.06%。均方根誤差比單一EEMD方法的均方根誤差降低了51.02%。由此可以看出，基于改進EEMD算法能夠在去除噪聲的同時，保留更多的信號特征，更適用于處理超聲檢測信號。

4 結論（Conclusion）

本文針對單一EEMD算法重構信號后不能很好地保留原始信號特征的問題，引入了PCA算法。基于EEMD聯合PCA 的信號處理方法能夠有效避免模態混疊現象，同時能夠消除信號中的噪聲，并且能保留更多的特征信號。通過仿真數據進行驗證的結果顯示，相較于EEMD算法，EEMD聯合PCA的信號處理方法有更好的信噪比及均方根誤差的表現，可為后續缺陷特征識別提供更好的支持，更適用于處理超聲信號。

作者簡介：

趙斯琪（1996-），女，碩士，助教。研究領域：信號處理，深度學習。

彭鈺瑩（1993-），女，碩士，講師。研究領域：人工智能，機器學習。