改進加權質心算法的集群協同定位理論研究

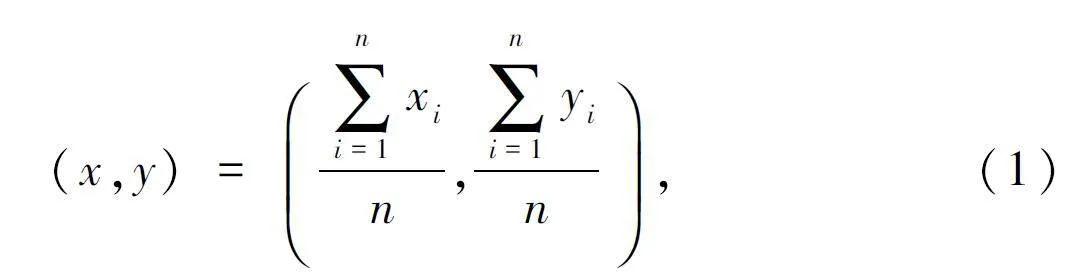
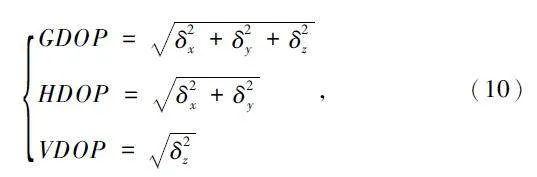
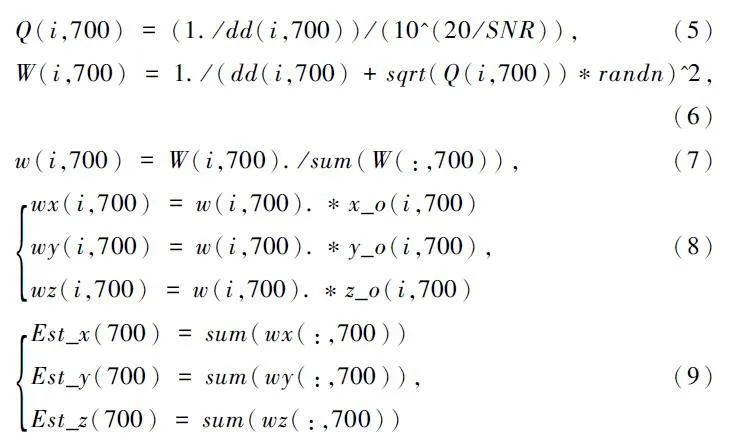
摘 要：無人機集群定位信息的獲取對于路徑規劃、探測、制導和協同控制等均具有重要意義，當前通常使用的全球導航衛星系統（Ｇｌｏｂａｌ Ｎａｖｉｇａｔｉｏｎ Ｓａｔｅｌｌｉｔｅ Ｓｙｓｔｅｍ，ＧＮＳＳ） 定位易受到干擾和欺騙的影響而處于拒止狀態，基于機間數據鏈的協同定位的用途日益凸顯。目前缺少獲得一致認同的在精度和計算量之間獲得較好平衡的協同定位算法，針對這一問題，對研究ＧＮＳＳ 拒止下基于機間測距的無人機集群協同定位方法進行了簡要介紹。搭建集群無人機協同定位分散融合定位架構，針對ＧＮＳＳ 拒止下集群無人機定位性能無法定量評估問題，建立集群協同定位精度定量評估模型，構建出典型任務場景下的無人機飛行軌跡和各歷元的機間測距信息。通過仿真試驗，利用包括加權質心算法、最小二乘法和網格法在內的多種算法解算得到無人機集群的相對位置信息，評估設定的典型場景下３ 種定位方法定位性能，解決ＧＮＳＳ 拒止下集群無人機定位誤差快速發散的問題。仿真結果表明，加權質心算法性價比最高，研究結論可為無人機集群定位提供一定的指導和幫助。

關鍵詞：全球導航衛星系統拒止環境；機間測距；協同定位

中圖分類號：ＴＰ３９３ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０７－１７７９－０７

０ 引言

無人機因體積較小、造價較低、機動性較強和隱蔽性較好等突出優點，近年來被越來越多地應用在軍事偵查、目標追蹤和地形勘察等領域［１］。例如，烏克蘭和俄羅斯均在戰場中使用了大量無人機用于偵察和攻擊作戰［２］，美軍在敘利亞戰爭中使用無人機獲得了較好的效果。然而，單架無人機由于受到尺寸、能源和載荷等因素的限制，難以滿足多樣化和復雜化的任務要求［３］，無人機集群的概念應運而生。

定位信息是無人機集群路徑規劃、避撞和協同偵察等任務的關鍵基礎信息，目前通常使用全球導航衛星系統（Ｇｌｏｂａｌ Ｎａｖｉｇａｔｉｏｎ Ｓａｔｅｌｌｉｔｅ Ｓｙｓｔｅｍ，ＧＮＳＳ）獲取無人機的位置信息，然而，由于ＧＮＳＳ 信號固有的脆弱性［４］，極易受到有意或無意干擾，甚至欺騙，導致無人機無法獲得定位信息而處于ＧＮＳＳ拒止狀態［５］。近年來，隨著機間數據鏈的不斷發展，機間測距精度越來越高，使得基于機間測距值的無人機集群定位成為可能，不僅可提高集群定位精度，還可在ＧＮＳＳ 拒止情況下獲得連續的定位結果，增強了系統的魯棒性。近些年國內外學者對集群無人機協同導航做了大量研究，無人機集群編隊技術發展迅速。

Ｌｉｕ 等［６］在導彈間引入數據鏈，利用無線電測距功能使得領彈與攻擊彈之間進行協同定位，對導彈定位方法進行了拓展，提高了導彈系統的定位精度。Ｓｈｅｎ 等［７］不再采用基于視覺的相對坐標估計方法，提出了一種超寬帶輔助的衛星／ 慣導緊耦合協同導航算法，利用機載超寬帶測距通信網絡在二維空間中感知無人機之間的距離實現對位置的估計，但該方法依賴衛星導航。另外針對全球導航定位系統拒止或受限情況，Ｓｉｖａｎｅｒｉ 等［８］提出了一種無人機－無人地面車輛協同導航方案，以提高無人機在ＧＮＳＳ 受限環境中的導航性能。Ｃａｕｓａ 等［９］提出了一種無人機－無人機協同策略。Ｘｉｏｎｇ 等［１０］研究了超寬帶與差分全球定位系統融合的相對導航方法。

集群無人機通過機間信息交互實現機間信息共享，進行無人機共同執行任務，并且增加無人機探索方式，實現資源優化配置，從而有效提高無人機工作性能。無人機協同工作時，需要互相了解各自的相對位置情況，以便相互輔助進行協同導航定位，以提高應用范圍和定位精度。因此，高精度、高可靠性的定位信息是無人機集群高效執行任務的重要基礎保障。本文重點研究ＧＮＳＳ 拒止環境下的無人機集群協同定位方法［１１］。

首先，搭建出集群無人機協同定位分散融合定位架構；然后，針對ＧＮＳＳ 拒止下集群無人機定位性能無法定量評估問題，建立集群協同定位精度定量評估模型，構建出典型任務場景下的無人機飛行軌跡和各歷元的機間測距信息，并解決ＧＮＳＳ 拒止下集群無人機定位誤差快速發散的問題；最后，為了驗證所提出的算法，利用Ｍａｔｌａｂ 仿真實驗對算法進行了分析，用加權質心算法、最小二乘法和網格法在內的多種算法解算得到估計位置無人機的相對位置信息，評估設定的典型場景下３ 種定位方法定位性能。

１ 定位算法理論

１． １ 質心定位算法原理

質心定位算法（Ｃｅｎｔｒｏｉｄ Ａｌｇｏｒｉｔｈｍ）是一種不需要測距的定位算法，通過計算網絡聯通性進行定位。其原理是以錨節點為圓心，以通過路徑損耗模型計算出的距離為半徑畫圓，計算出形成的公共區域的質心坐標。可得出未知節點Ａ（ｘ，ｙ）的質心算法公式為：

式中：（ｘ，ｙ）為未知節點坐標，（ｘｉ，ｙｉ）為未知節點通信范圍內第ｉ 個錨節點坐標，ｎ 為未知節點通信范圍內錨節點數量。

質心定位算法計算簡單、開銷小、容易實現，但是定位誤差大，而且定位精度極易受到錨節點數量和均勻程度的影響，需要對算法進行適當的優化處理。

１． ２ 最小二乘法定位算法原理

最小二乘法［１２］又稱最小平方算法，作為數據處理和誤差計算的一種數學手段被廣泛應用于工程實踐和實驗計算［１３］，其原理是利用實驗數據在滿足誤差平方和最小的情況下，解得最佳值［１４］。利用最小二乘法可以簡便地求得未知的數據，使得這些觀測數據與這個數據誤差的平方和最小。在確定回歸直線時，它使確定的回歸直線與所有觀測數據對應點的縱向距離平方和最小。一般形式可表示為目標函數＝ Σ（觀測值－理論值） ２ ，和號也可以是積分號。理論值根據設定的模型計算，其中含有未知參數，其值是以目標函數達到最小值的準則進行估計。

１． ３ 網格法定位算法原理

網格法與質心算法原理相似，已知節點的平均數為未知節點坐標，但網格法需要更多的已知節點，對環境要求較高。

２ 改進的加權質心定位算法原理

質心定位算法是Ｎｉｒｕｐａｍａ Ｂｕｌｕｓｕ 等提出的一種粗精度定位算法。傳統質心算法［１５］中沒有對已知的各組數據的權值進行差異化處理，對誤差不同的數據用相同的權值。當未知節點周圍的錨節點分布不均勻時，定位精度下降［１６］。在解方程ＡＸ ＝ ｂ時，在理想條件下，ｂ 為準確值，用多邊定位算法可得到使方程兩邊相等的準確的Ｘ。但實際情況ｂ 是有誤差的，用最小二乘法解方程時，ｂ 的誤差越大，得到的Ｘ 誤差就越大，降低了定位精度。針對無人機定位中傳感器節點由于無人機之間距離、噪聲存在影響信號強度的接收而存在的誤差，在利用無人機之間距離、信噪比以及正態分布隨機量的基礎上提出了一種基于優化定位精度的加權質心定位算法［１７］。在加權質心定位算法［１８］中，錨節點對質心位置的影響是通過權值大小來判斷的，綜合考慮錨節點與未知節點的遠近程度對對未知節點的影響，給每個錨節點賦予不同的權值，不同的權值對不同誤差的數據差別處理，較大誤差的數據對應較小的權值，較小誤差的數據對應較大的權值［１９］，優化了傳統質心定位算法，提高了定位的準確性。本文所用的加權質心定位算法原理方程如下：

Ｑ（ｉ，ｋ） ＝ （１． ／ ｄｄ（ｉ，ｋ））／ （１０＾（２０ ／ ＳＮＲ））， （２）

Ｗ（ｉ，ｋ） ＝ １． ／ （ｄｄ（ｉ，ｋ）＋ ｓｑｒｔ（Ｑ（ｉ，ｋ））*ｒａｎｄｎ）＾２，（３）

ｗ（ｉ，ｋ） ＝ Ｗ（ｉ，ｋ）． ／ ｓｕｍ（Ｗ（：，ｋ））， （４）

式中：ｉ 表示無人機編號，ｋ 表示時間，ｄｄ（ｉ，ｋ）表示ｋ時刻ｉ 架無人機到目標無人機的距離，ＳＮＲ 表示信噪比，賦值５０；ｒａｎｄｎ 表示正態分布的隨機量，ｗ（ｉ，ｋ）表示ｋ 時刻編號為ｉ 的無人機的權值。

用１６ 號無人機在７００ ｓ 時刻的估計位置計算為例描述權值代入算法后的具體公式：

式中：ｘ＿ｏ、ｙ＿ｏ、ｚ＿ｏ 為無人機位置，Ｅｓｔ＿ｘ、Ｅｓｔ＿ｙ、Ｅｓｔ＿ｚ為１６ 號無人機估計位置，ｗｘ、ｗｙ、ｗｚ 為過渡變量。

３ 實驗分析

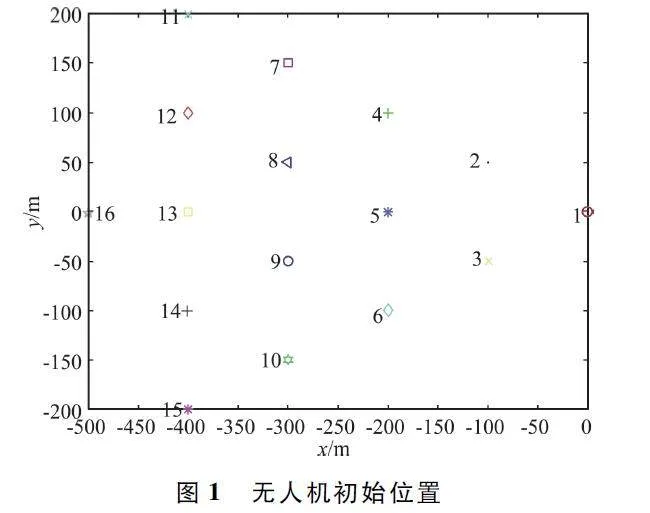
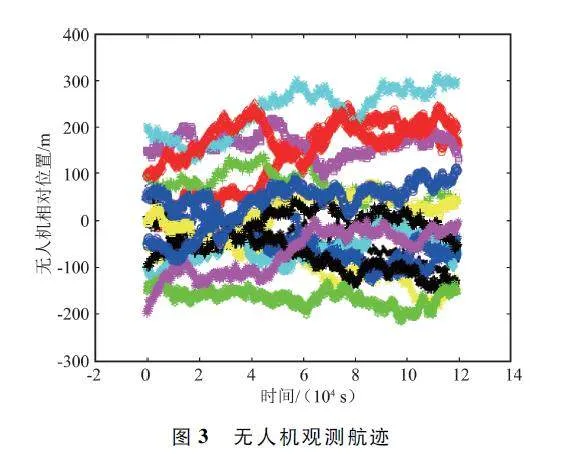
為了驗證所提出的算法，利用Ｍａｔｌａｂ 仿真實驗對算法進行了分析［２０］，仿真實驗設計思路為研究１６ 架無人機以固定陣型在１ ２００ ｓ 飛行時間內，任意時刻通過已知無人機位置對未知無人機進行定位。１６ 架無人機為１６ 個節點，通過設置其初始位置、飛行航跡，模擬真實無人機飛行過程。本文以９ 號無人機為未知位置無人機，計算其在３ 種定位方法下的估計位置。考慮到風力、天氣和通信設備延遲等不可抗因素的影響，無人機航跡設置時加入過程噪聲和觀測噪聲，兩噪聲都屬于正態分布隨機噪聲。無人機在三維空間內飛行，故設計航跡分別從ｘ 軸、ｙ 軸、ｚ 軸３ 個方位考慮，ｘ 軸的航跡設置為無人機初始位置、飛機自身速度、過程噪聲和觀測噪聲的疊加，ｙ 軸和ｚ 軸的航跡設置為無人機初始位置、過程噪聲和觀測噪聲的疊加。以７００ ｓ 時刻為例，根據上述步驟用３ 種方法對無人機模擬定位。無人機初始位置、無人機終點位置以及無人機觀測航跡如圖１ ～ 圖３ 所示。

從圖１ 可看出，無人機是在典型場景下以固定構型起飛。從圖２ 可以看出，在終點時無人機隊形和起點相比較，由于過程噪聲和觀測噪聲的存在差距較大。從圖３ 可以看出，無人機整個飛行航跡較為平穩。

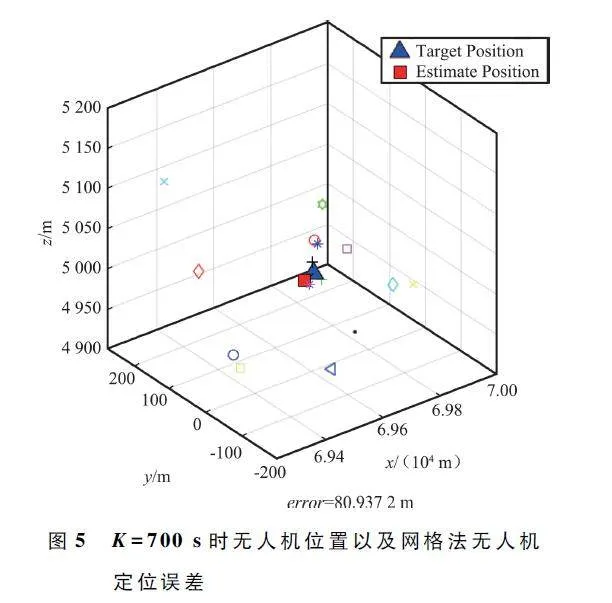
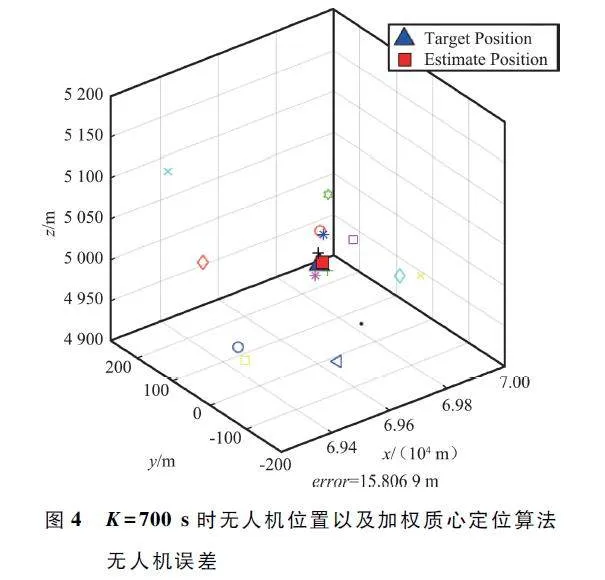
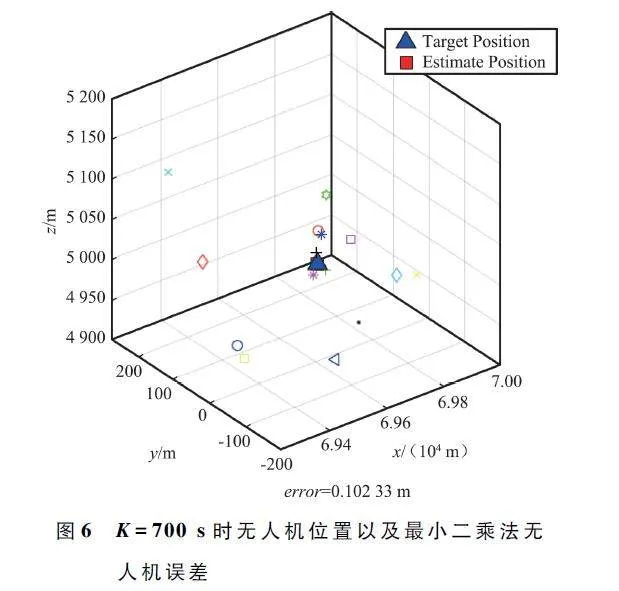
圖４ ～ 圖６ 分別是７００ ｓ 時無人機在三維空間內位置以及在加權質心算法、網格法和最小二乘法３ 種定位方法下，９ 號無人機估計位置以及估計位置與實際位置誤差。對比這３ 幅圖可以看出，７００ ｓ 時最小二乘法誤差最小，加權質心算法次之，網格法誤差最大。

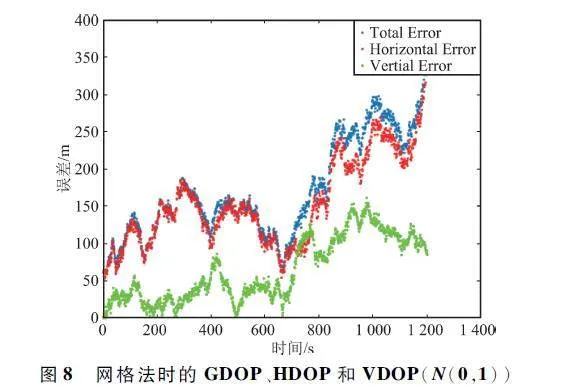
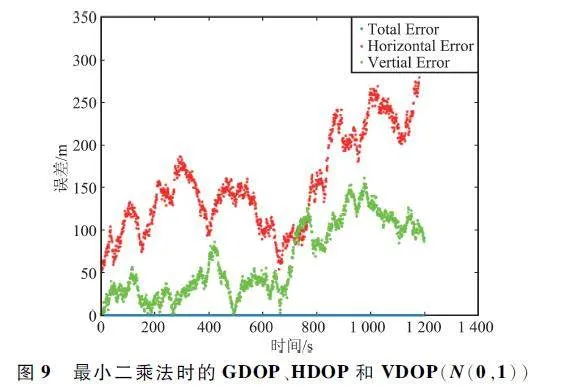
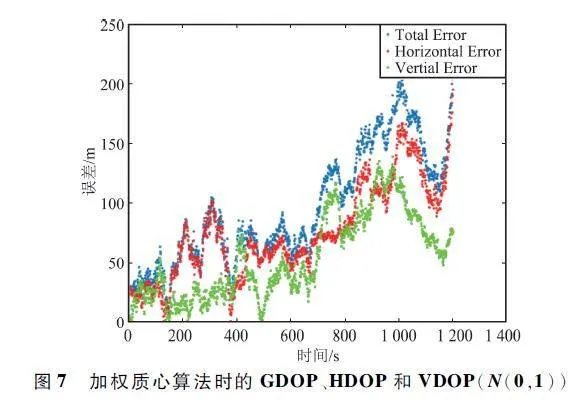
圖７ ～ 圖９ 是過程噪聲和觀測噪聲都服從正態分布Ｎ（０，１ ）時，整個無人機系統在飛行時間段內在加權質心算法、網格法和最小二乘法３ 種算法下的誤差曲線。使用Ｍａｔｌａｂ 計算３ 種算法程序所用時間，加權算法用時０． ６５１ ６７５ ｓ，網格法用時０． ３２６ ７４０ ｓ，最小二乘法用時１４． ８１１ ６３１ ｓ。

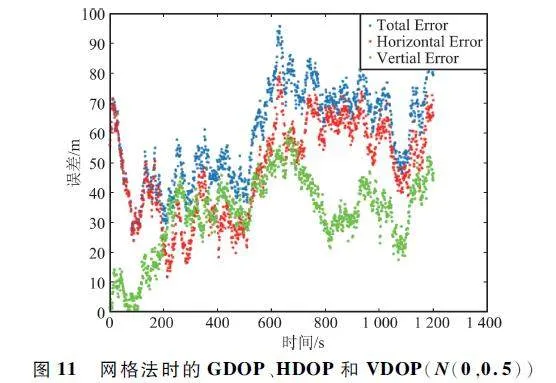
圖１０ ～ 圖１２ 是過程噪聲和觀測噪聲都服從正態分布Ｎ（０，０． ５）時，整個無人機系統在飛行時間段內在加權質心算法、網格法和最小二乘法３ 種算法下的誤差曲線。使用Ｍａｔｌａｂ 計算３ 種算法程序所用時間，加權算法用時０． ６３６ １６５ ｓ，網格法用時０． ３０９ ９８６ ｓ，最小二乘法用時４２． ７７１ ３５０ ｓ。

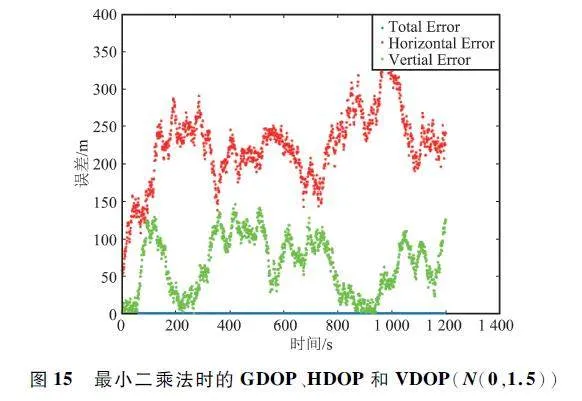
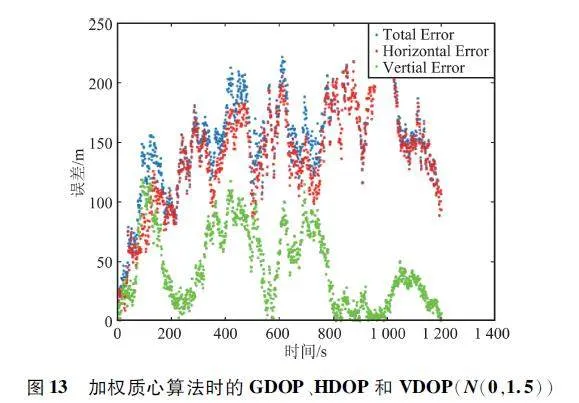
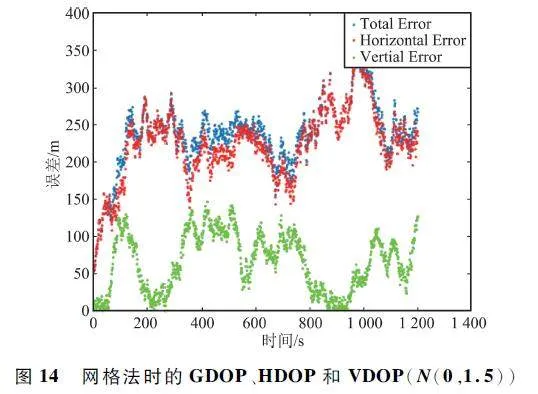
圖１３ ～ 圖１５ 是過程噪聲和觀測噪聲都服從正態分布Ｎ（０，１． ５）時，整個無人機系統在飛行時間段內在加權質心算法、網格法和最小二乘法３ 種算法下的誤差曲線。使用Ｍａｔｌａｂ 計算３ 種算法程序所用時間，加權算法用時０． ６７０ ０３６ ｓ，網格法用時００． ３２５ ８０５ ｓ，最小二乘法用時２５． ２０５ ４８８ ｓ。

分析圖７ ～ 圖１５，藍色線為總誤差，用ＧＤＯＰ 表示；紅色線為水平誤差，用ＨＤＯＰ 表示；綠色線為高程誤差，用ＶＤＯＰ 表示。ＧＤＯＰ、ＨＤＯＰ、ＶＤＯＰ 計算如下：

式中：δｘ、δｙ、δｚ 分別為ｘ、ｙ、ｚ 方向上的定位誤差標準差，即估計值與真實值之差。

圖７ ～ 圖１５ 就是無人機整個飛行過程中，目標９ 號無人機在加權質心算法，網格法，最小二乘法３ 種定位算法下的ＧＤＯＰ、ＨＤＯＰ、ＶＤＯＰ。對比圖７ ～ 圖１５ 可以看出，過程誤差和觀測誤差無論是服從正態分布Ｎ（０，１）或Ｎ（０，０． ５）還是Ｎ（０，１． ５），最小二乘法定位精度最高，加權質心算法次之，網格法定位精度最低。雖然在無人機整個飛行過程中用最小二乘法定位，目標飛機的估計位置和真實位置的總誤差、水平誤差、高程誤差較小，但依據Ｍａｔｌａｂ程序統計時間來看，相比較加權質心算法，最小二乘法計算量很大，加權質心算法定位精度較高、成本較低、計算量適中。

４ 結論

ＧＮＳＳ 拒止條件下無人機集群的高精度、高連續性定位結果對于協同探測、感知和攻擊等任務均具有重要價值，本文利用無人機節點間的相對距離測量值，采用不同的協同定位算法評估得到典型場景下的集群協同定位性能。

本文改進了加權質心算法系數的算法，使得有用的數據對應更大的權值。通過本文的研究得出以下結論：

① 網格法定位精度最差且定位成本最高；加權質心算法和最小二乘法定位成本大致相當，雖然最小二乘法定位精度高于加權質心算法，但最小二乘法計算量龐大，加權質心算法計算量適中、定位精度較高，對于追求平衡精度和計算量的協同定位算法具有一定意義，是性價比最高的定位算法。

② 在無人機飛行過程中，噪聲服從正態分布時，方差越大，定位誤差越大。

③ 本文改進的加權質心定位算法，提高了無人機的定位精度。

本文對ＧＮＳＳ 拒止下集群協同定位理論進行了一定的研究，但仍有許多不足之處，只是在Ｍａｔｌａｂ自行搭建無人機飛行環境，并沒有讓無人機在實地場景中去飛，接下來，將繼續研究更加高效的針對無人機協同導航的算法。

參考文獻

［１］ ＦＡＮ Ｂ Ｋ，ＬＩ Ｙ，ＺＨＡＮＧ Ｒ Ｙ，ｅｔ ａｌ． Ｒｅｖｉｅｗ ｏｎ ｔｈｅ Ｔｅｃｈｎｏｌｏｇｉｃａｌ Ｄｅｖｅｌｏｐｍｅｎｔ ａｎｄ Ａｐｐｌｉｃａｔｉｏｎ ｏｆ ＵＡＶ Ｓｙｓｔｅｍｓ［Ｊ ］． Ｃｈｉｎｅｓｅ Ｊｏｕｒｎａｌ ｏｆ Ｅｌｅｃｔｒｏｎｉｃｓ，２０２０，２９ （２ ）：１９９－２０７．

［２］ 馮楊，蔣超，崔玉偉． 俄烏沖突中無人機作戰運用及啟示［Ｊ］． 中國軍轉民，２０２２（２３）：３５－４０．

［３］ ＺＯＵ Ｙ Ｆ，ＰＡＧＩＬＬＡ Ｐ Ｒ，ＲＡＴＬＩＦＦ Ｒ Ｔ． Ｄｉｓｔｒｉｂｕｔｅｄ Ｆｏｒｍａｔｉｏｎ Ｆｌｉｇｈｔ Ｃｏｎｔｒｏｌ Ｕｓｉｎｇ Ｃｏｎｓｔｒａｉｎｔ Ｆｏｒｃｅｓ［Ｊ］． Ｊｏｕｒｎａｌｏｆ Ｇｕｉｄａｎｃｅ，Ｃｏｎｔｒｏｌ，ａｎｄ Ｄｙｎａｍｉｃｓ，２００９，３２ （１ ）：１１２－１２０．

［４］ ＣＨＥＮ Ｍ Ｌ，ＺＨＡＮ Ｘ，ＬＩＵ Ｂ，ｅｔ ａｌ． ＧＮＳＳ ＶｕｌｎｅｒａｂｉｌｉｔｙＮｅｔｗｏｒｋ Ｒｉｓｋ Ａｓｓｅｓｓｍｅｎｔ ａｎｄ Ａｌｌｅｖｉａｔｉｏｎ Ｓｔｒａｔｅｇｉｅｓ Ｃｏｎｓｉｄｅｒｉｎｇ Ｅｆｆｉｃｉｅｎｃｙ Ｃｏｓｔ ［Ｊ ］． Ｊｏｕｒｎａｌ ｏｆ Ａｅｒｏｎａｕｔｉｃｓ，Ａｓｔｒｏｎａｕｔｉｃｓ ａｎｄ Ａｖｉａｔｉｏｎ，２０１８，５０（２）：１６１－１７４．

［５］ ＣＨＥＮ Ｍ Ｌ，ＸＩＥ Ｎ，ＨＵＡＮＧ Ｚ Ｊ，ｅｔ ａｌ． ５Ｇ Ｂａｓｅｄ ＶｅｈｉｃｌｅＬｏｃａｌｉｚａｔｉｏｎ ｉｎ ＧＮＳＳ Ｄｅｎｉｅｄ Ｅｎｖｉｒｏｎｍｅｎｔｓ ａｎｄ Ｉｔｓ Ｉｍｐｒｏｖｅｍｅｎｔ Ｕｔｉｌｉｚｉｎｇ ＳＲＣＫＦ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ａｅｒｏｎａｕｔｉｃｓ，Ａｓｔｒｏｎａｕｔｉｃｓ ａｎｄ Ａｖｉａｔｉｏｎ，２０２２，５４（４）：４３３－４５０．

［６］ ＬＩＵ Ｊ Ｃ，ＺＨＡＮＧ Ｊ Ｊ，ＴＡＮ Ｌ Ｆ． Ａ Ｎｅｗ Ｄａｔａ Ｆｕｓｉｏｎ Ｍｅｔｈｏｄ ｆｏｒ Ｍｕｌｔｉｍｉｓｓｉｌｅ Ｃｏｏｐｅｒａｔｉｖｅ Ｌｏｃａｌｉｚａｔｉｏｎ［Ｃ］∥Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ ２０１２ Ｐｒｏｇｎｏｓｔｉｃｓ ａｎｄ Ｓｙｓｔｅｍ ＨｅａｌｔｈＭａｎａｇｅｍｅｎｔ Ｃｏｎｆｅｒｅｎｃｅ （ＰＨＭ２０１２ Ｂｅｉｊｉｎｇ ）． Ｂｅｉｊｉｎｇ：ＩＥＥＥ，２０１２：１－４．

［７］ ＳＨＥＮ Ｆ，ＣＨＥＯＮＧ Ｊ Ｗ，ＤＥＭＰＳＴＥＲ Ａ Ｇ． Ａｎ ＵＷＢｂａｓｅｄ Ｒａｎｇｅ ／ ＧＰＳ Ｔｉｇｈｔ Ｉｎｔｅｒｇｒａｔｉｏｎ Ａｐｐｒｏａｃｈ ｆｏｒＲｅｌａｔｉｖｅ Ｐｏｓｉｔｉｏｎｉｎｇ ｉｎ ＶＡＮＥＴｓ ［Ｊ ］． ＭｅａｓｕｒｅｍｅｎｔＳｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ，２０１５，２６（４）：０４５００３．

［８］ ＳＩＶＡＮＥＲＩ Ｖ Ｏ，ＧＲＯＳＳ Ｊ Ｎ． ＵＧＶｔｏＵＡＶ ＣｏｏｐｅｒａｔｉｖｅＲａｎｇｉｎｇ ｆｏｒ Ｒｏｂｕｓｔ Ｎａｖｉｇａｔｉｏｎ ｉｎ ＧＮＳＳｃｈａｌｌｅｎｇｅｄ Ｅｎｖｉｒｏｎｍｅｎｔｓ［Ｊ］． Ａｅｒｏｓｐａｃｅ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ，２０１７，７１：２４５－２５５．

［９］ ＣＡＵＳＡ Ｆ，ＶＥＴＲＥＬＬＡ Ａ Ｒ，ＦＡＳＡＮＯ Ｇ，ｅｔ ａｌ． ＭｕｌｔｉＵＡＶ Ｆｏｒｍａｔｉｏｎ Ｇｅｏｍｅｔｒｉｅｓ ｆｏｒ Ｃｏｏｐｅｒａｔｉｖｅ Ｎａｖｉｇａｔｉｏｎ ｉｎＧＮＳＳｃｈａｌｌｅｎｇｉｎｇ Ｅｎｖｉｒｏｎｍｅｎｔｓ ［Ｃ］∥ ２０１８ ＩＥＥＥ ／ ＩＯＮＰｏｓｉｔｉｏｎ，Ｌｏｃａｔｉｏｎ ａｎｄ Ｎａｖｉｇａｔｉｏｎ Ｓｙｍｐｏｓｉｕｍ（ＰＬＡＮＳ）．Ｍｏｎｔｅｒｅｙ：ＩＥＥＥ，２０１８：７７５－７８５．

［１０］ ＸＩＯＮＧ Ｊ，ＸＩＯＮＧ Ｚ，ＹＵ Ｙ Ｊ，ｅｔ ａｌ． Ｃｌｏｓｅ Ｒｅｌａｔｉｖｅ Ｎａｖｉｇａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｕｎｍａｎｎｅｄ Ａｅｒｉａｌ Ｖｅｈｉｃｌｅ Ａｉｄｅｄ ｂｙＵＷＢ Ｒｅｌａｔｉｖｅ Ｍｅａｓｕｒｅｍｅｎｔ ［Ｊ ］． Ｊｏｕｒｎａｌ ｏｆ ＣｈｉｎｅｓｅＩｎｅｒｔｉａｌ Ｔｅｃｈｎｏｌｏｇｙ，２０１８，２６（３）：７２－７７．

［１１］ ＭＯＨＡＭＭＡＤＡＢＡＤＩ Ｐ Ｈ，ＶＡＬＡＥＥ Ｓ． Ｃｏｏｐｅｒａｔｉｖｅ ＮｏｄｅＰｏｓｉｔｉｏｎｉｎｇ ｉｎ Ｖｅｈｉｃｕｌａｒ Ｎｅｔｗｏｒｋｓ Ｕｓｉｎｇ Ｉｎｔｅｒｎｏｄｅ Ｄｉｓｔａｎｃｅ Ｍｅａｓｕｒｅｍｅｎｔｓ［Ｃ］∥２０１４ ＩＥＥＥ ２５ｔｈ Ａｎｎｕａｌ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｐｅｒｓｏｎａｌ，Ｉｎｄｏｏｒ，ａｎｄ ＭｏｂｉｌｅＲａｄｉｏ Ｃｏｍｍｕｎｉｃａｔｉｏｎ（ＰＩＭＲＣ）． Ｗａｓｈｉｎｇｔｏｎ Ｄ． Ｃ． ：ＩＥＥＥ，２０１４：１４４８－１４５２．

［１２］ ＢＪ？ＲＣＫ Ａ． Ｌｅａｓｔ Ｓｑｕａｒｅｓ Ｍｅｔｈｏｄｓ［Ｊ］． Ｈａｎｄｂｏｏｋ ｏｆ Ｎｕｍｅｒｉｃａｌ Ａｎａｌｙｓｉｓ，１９９０，１：４６５－６５２．

［１３］ ＫＩＭ Ｄ Ｓ，ＫＩＭ Ｊ Ｃ，ＫＩＭ Ｓ Ｈ． Ａ Ｓｔｕｄｙ ｏｎ ｔｈｅ Ｐａｔｉｅｎｔ Ｌｏｃａｔｉｏｎ Ｍｏｎｉｔｏｒｉｎｇ Ｓｙｓｔｅｍ Ｂａｓｅｄ ｏｎ ＲＦＩＤＲＳＳＩ ［Ｊ ］．Ｈｅａｌｔｈ Ｃａｒｅ Ｉｎｆｏｒｍａｔｉｃｓ Ｒｅｓｅａｒｃｈ，２００９，１５（１）：４１－４８．

［１４］ ＦＡＮ Ｗ Ｈ，ＹＵ Ｌ，ＷＡＮＧ Ｚ，ｅｔ ａｌ． Ｔｈｅ Ｅｆｆｅｃｔ ｏｆ Ｗａｌｌ Ｒｅｆｌｅｃｔｉｏｎ ｏｎ Ｉｎｄｏｏｒ Ｗｉｒｅｌｅｓｓ Ｌｏｃａｔｉｏｎ Ｂａｓｅｄ ｏｎ ＲＳＳＩ［Ｃ］∥２０１４ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｒｏｂｏｔｉｃｓ ａｎｄＢｉｏｍｉｍｅｔｉｃｓ． Ｂａｌｉ：ＩＥＥＥ，２０１５：１３８０－１３８４．

［１５］ ＬＩＵ Ｙ Ｊ，ＪＩＮ Ｍ Ｌ，ＣＵＩ Ｃ Ｙ． Ｃｏｒｒｅｃｔｉｏｎ Ｗｅｉｇｈｔｅｄ ＣｅｎｔｒｏｉｄＬｏｃａｌｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｗｉｒｅｌｅｓｓ Ｓｅｎｓｏｒ ＮｅｔｗｏｒｋｓＢａｓｅｄ ｏｎ ＲＳＳＩ［Ｊ］． Ｓｅｎｓｏｒｓ，２０１０（５）：７１７－７１８．

［１６］ 高美鳳，尹持俊． 基于ＵＡＶ 的無線傳感器網絡加權質心定位算法［Ｊ］． 傳感技術學報，２０２１，３４（４）：５３９－５４５．

［１７］ ＷＡＮＧ Ｊ，ＵＲＲＩＺＡ Ｐ，ＨＡＮ Ｙ Ｘ，ｅｔ ａｌ． Ｗｅｉｇｈｔｅｄ ＣｅｎｔｒｏｉｄＬｏｃａｌｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ： Ｔｈｅｏｒｅｔｉｃａｌ Ａｎａｌｙｓｉｓ ａｎｄＤｉｓｔｒｉｂｕｔｅｄ Ｉｍｐｌｅｍｅｎｔａｔｉｏｎ ［Ｊ ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎＷｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１１，１０（１０）：３４０３－３４１３．

［１８］ ＫＯＮＧ Ｑ Ｒ，ＹＡＮＧ Ｘ Ｙ，ＤＡＩ Ｘ Ｊ． Ａｎ Ｉｍｐｒｏｖｅｄ ＷｅｉｇｈｔｅｄＣｅｎｔｒｏｉｄ Ｌｏｃａｌｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ［Ｃ］∥ ２０１０ ＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅ ｏｎ Ｃｙｂｅｒｅｎａｂｌｅｄ Ｄｉｓｔｒｉｂｕｔｅｄ Ｃｏｍｐｕｔｉｎｇ ａｎｄＫｎｏｗｌｅｄｇｅ Ｄｉｓｃｏｖｅｒｙ． ［Ｓ． ｌ． ：ｓ． ｎ． ］，２０１０：４００－４０５．

［１９］ 陳維克，李文鋒，首珩，等． 基于ＲＳＳＩ 的無線傳感器網絡加權質心定位算法［Ｊ］． 武漢理工大學學報（交通科學與工程版），２００６（２）：２６５－２６８．

［２０］ ＺＨＯＵ Ｌ Ｆ，ＭＡ Ｓ Ｋ． Ｉｍｐｒｏｖｅｄ Ｈｙｂｒｉｄ Ｌｏｃａｌｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ ｏｆ Ｍａｘｉｍｕｍ Ｌｉｋｅｈｏｏｄ ａｎｄ Ｃｅｎｔｒｏｉｄ ＬｏｃａｌｉｚａｔｉｏｎＢａｓｅｄ ｏｎ ＲＳＳＩ［Ｃ］∥２０１７ ４ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎＩｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅ ａｎｄ Ｃｏｎｔｒｏｌ Ｅｎｇｉｎｅｅｒｉｎｇ． Ｃｈａｎｇｓｈａ：ＩＥＥＥ，２０１７：３８５－３８９．

作者簡介

張薇薇 女，（１９９６—），碩士研究生。主要研究方向：ＧＮＳＳ 拒止下基于機間測距集群協同定位理論。

劉美紅 女，（１９８４—），博士，副教授。主要研究方向：信號調制及數據融合算法。

陳懋霖 男，（１９９０—），博士，助理研究員。主要研究方向：ＧＮＳＳ高精度定位應用、協同導航、綜合ＰＮＴ 技術。

李艷霞 女，（１９９５—），碩士研究生。主要研究方向：信息安全之企業網絡下上網行為管理。

王 章 男，（１９８５—），工程師。主要研究方向：地面遙測遙控、數據處理、安控加密技術。

基金項目：山西省基礎研究計劃項目（２０２１０３０２１２２３０２５）；中國工程物理研究院創新發展基金（２０２１００４７）