相似三角形的存在性問題解題策略
2024-08-26 00:00:00蘇玉
初中生學習指導·中考版 2024年3期


相似三角形的存在性問題是遼寧省中考數(shù)學試卷中常見的一種題型,下面舉例介紹此類問題的解題思路.
考題再現(xiàn)
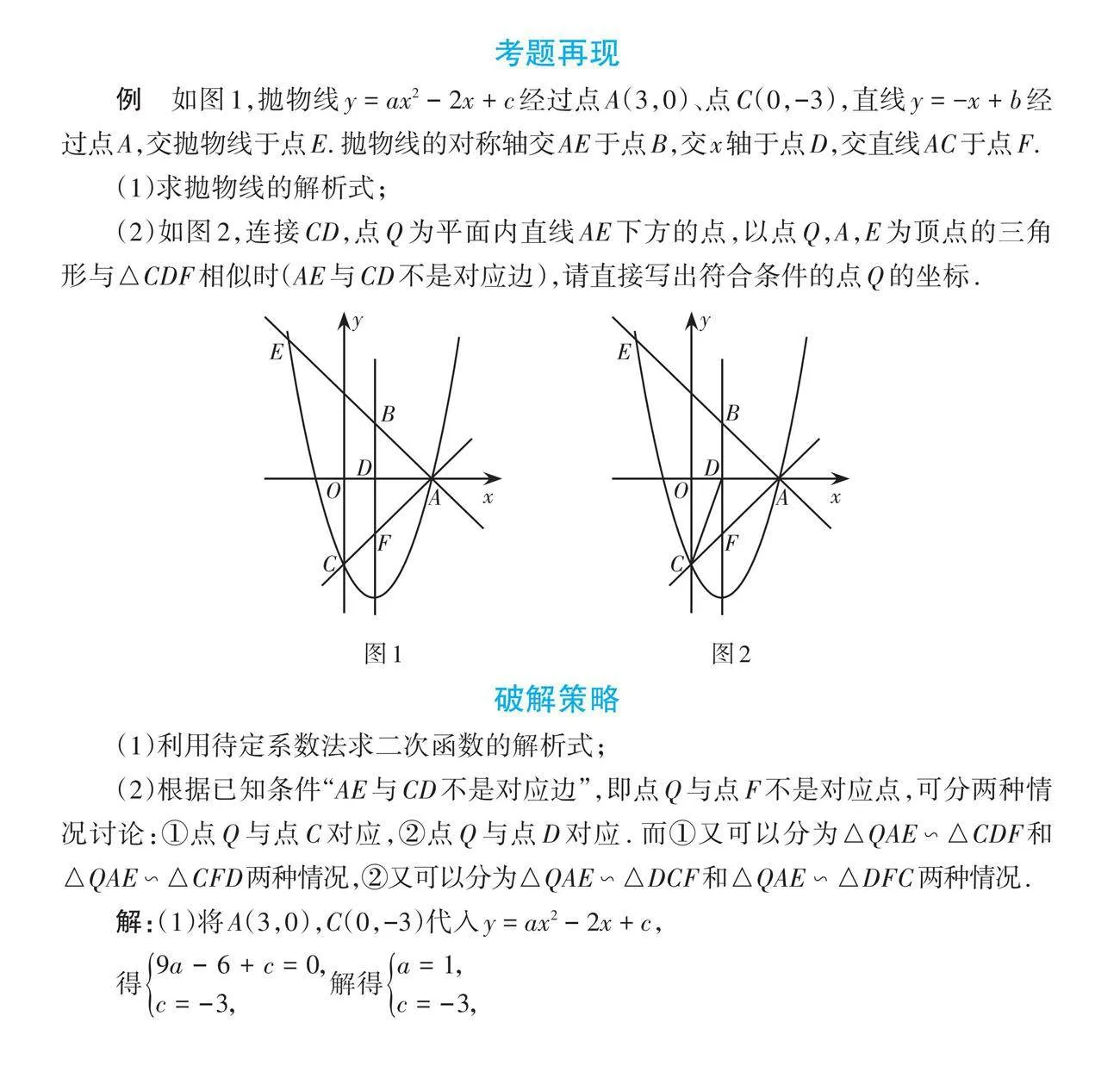
例 如圖1,拋物線y = ax2 - 2x + c經(jīng)過點A(3,0)、點C(0,-3),直線y = -x + b經(jīng)過點A,交拋物線于點E. 拋物線的對稱軸交AE于點B,交x軸于點D,交直線AC于點F.
(1)求拋物線的解析式;
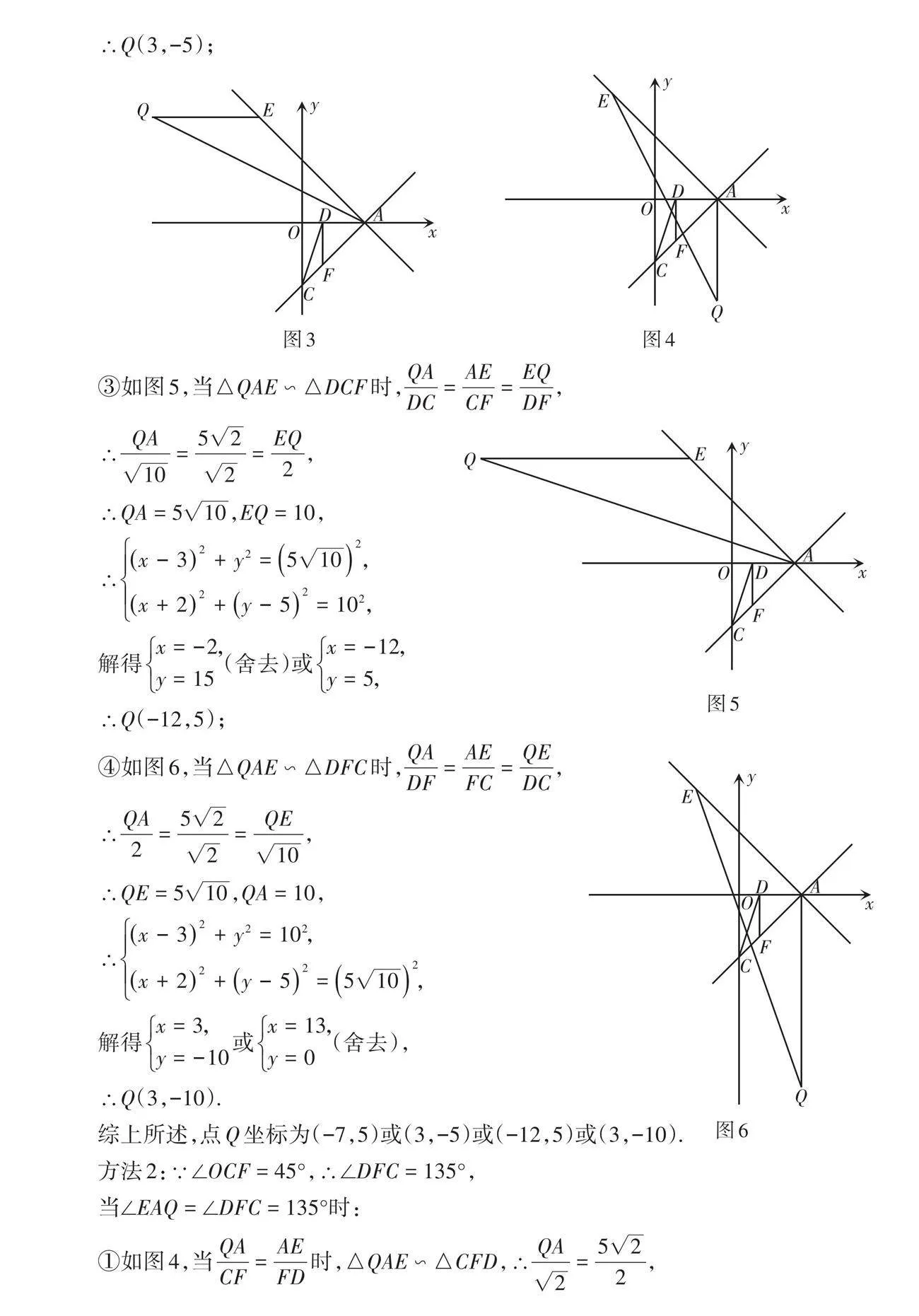
(2)如圖2,連接CD,點Q為平面內(nèi)直線AE下方的點,以點Q,A,E為頂點的三角形與△CDF相似時(AE與CD不是對應邊),請直接寫出符合條件的點Q的坐標.
破解策略
(1)利用待定系數(shù)法求二次函數(shù)的解析式;
(2)根據(jù)已知條件“AE與CD不是對應邊”,即點Q與點F不是對應點,可分兩種情況討論:①點Q與點C對應,②點Q與點D對應. 而①又可以分為△QAE ∽ △CDF和△QAE ∽ △CFD兩種情況,②又可以分為△QAE ∽ △DCF和△QAE ∽ △DFC兩種情況.

