挖掘機斗桿結構應力神經網絡建模

摘 要：為了研究斗桿結構應力神經網絡建模方法，在分析不同典型工況下斗桿結構的應力分布特征基礎上，確定斗桿結構的應力特征截面，分析斗桿結構各尺寸參數對各特征截面應力的靈敏度，據此確定斗桿結構應力神經網絡模型的輸入變量，進行結構應力神經網絡建模，并對不同神經網絡模型結構進行預測誤差對比分析。結果表明：所建立的模型可快速預測斗桿結構特征截面的應力，實訓樣本預測誤差小于10％。

關鍵詞：挖掘機；斗桿結構；BP神經網絡；應力預測；應力特征截面

中圖分類號：TP391.9 文獻標志碼：B 文章編號：1671-5276（2024）04-0154-07

Modeling of Stress Neural Network for Excavator Bucket Rod Structure

LI Jun， LUO Chengxu， LIN Shuwen

（School of Mechanical Engineering and Automation， Fuzhou University， Fuzhou 350108， China）

Abstract：To study the modeling method of the lever structure of stress neural network， based on the analysis of the stress distribution characteristics of the bucket lever structure under different typical conditions， determines the stress characteristic section of the bucket lever structure， and analyzes the sensitivity of the size parameters of the bucket lever structure to the stress of each feature section. Accordingly， the input variables of the stress neural network model of the bucket lever structure is defined， the model of the structural stress neural network is established， and the prediction error of different neural network model structures is compared and analyzed. The results show that the established neural network model of bucket structure can swiftly predict the stress of bucket structure section with prediction error less than 10%.

Keywords：excavator; bucket rod structure; BP neural network; stress prediction; stress characteristic cross section

0 引言

挖掘機斗桿結構優化設計過程中應力約束是斗桿結構整體結構強度能否滿足設計要求的關鍵。傳統優化設計過程中主要通過調用有限元軟件進行應力計算以實現結構應力約束^[1]。尋優過程中反復調用有限元軟件進行分析，影響優化效率。文獻[2-3]通過建立神經網絡預測模型來實現優化過程的應力計算，這種方式可以節省在優化過程中需要調用有限元軟件而消耗的大量時間，提高了優化效率。但是由于其斗桿結構的尺寸變量選擇不夠合理導致尺寸變量與結構件應力相關性不強，結構應力模型預測精度較低。因此，有必要探討更為合理的斗桿結構應力神經網絡建模變量的選擇及建模的新方法，以提高模型的預測精度，從而提高斗桿結構優化過程的速度和質量。

1 斗桿結構應力特征截面的選取

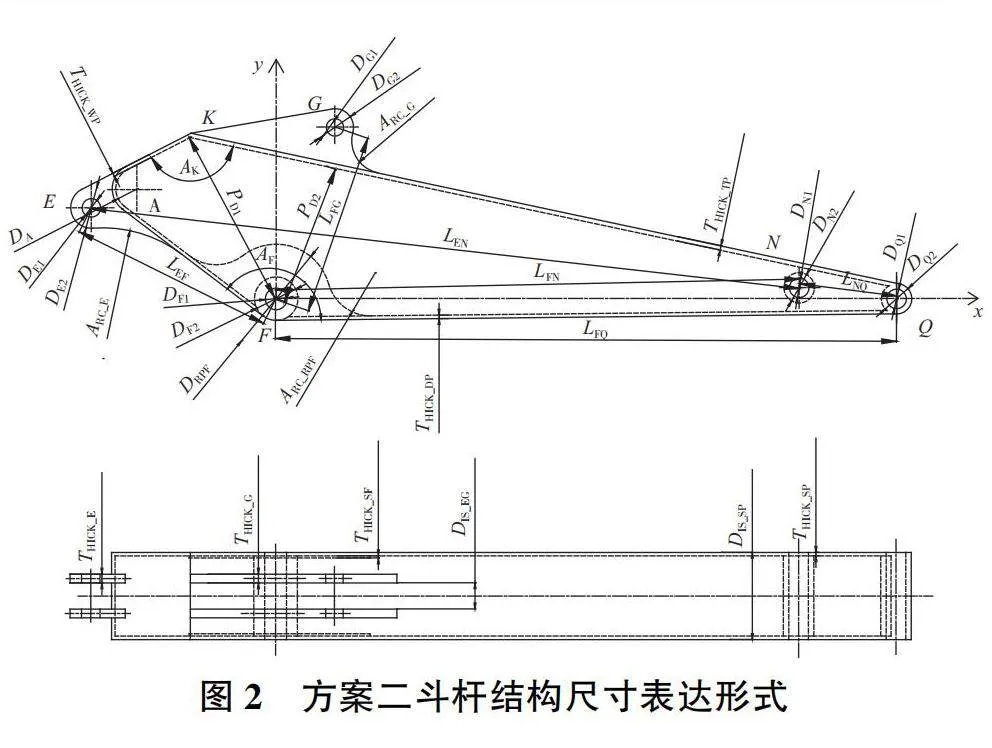
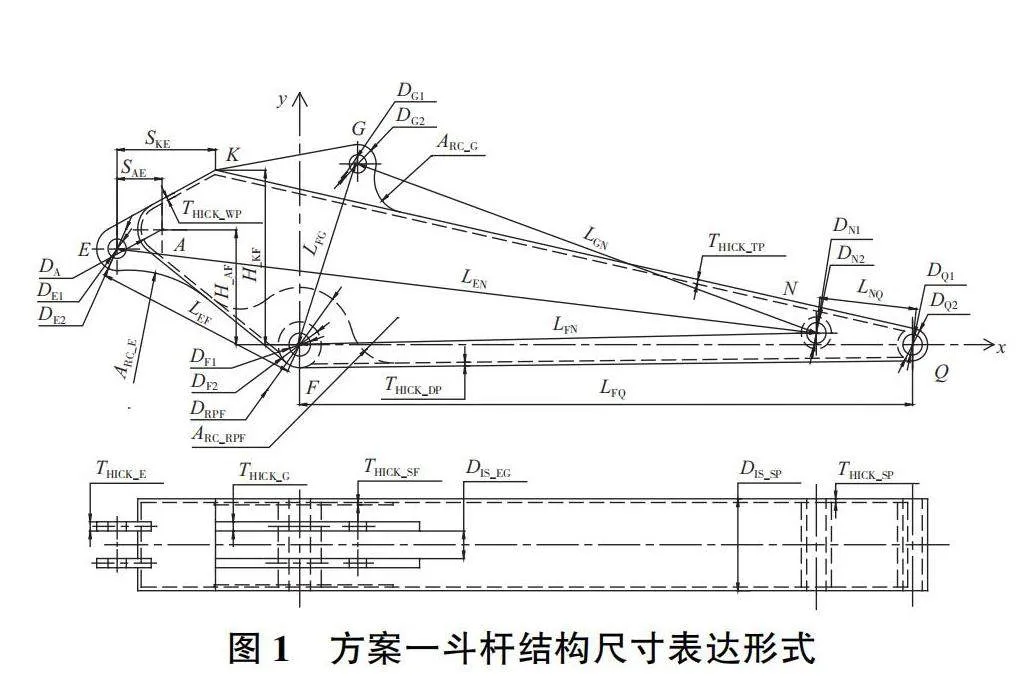
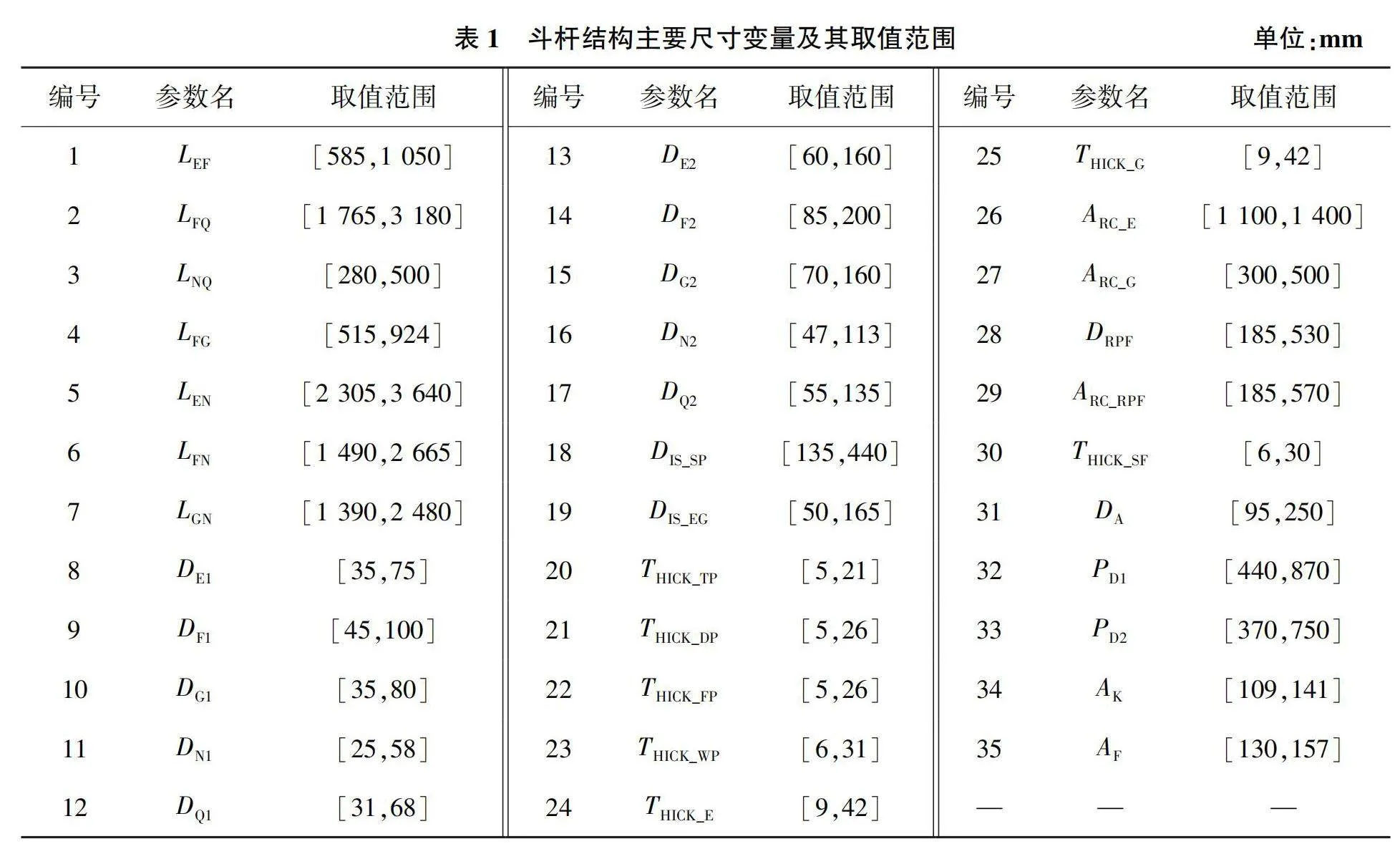
文獻[4]采用如圖1所示（簡稱“方案一”）的斗桿結構尺寸表達形式，以其尺寸變量作為斗桿結構應力建模的輸入變量，結構應力預測精度較低，預測模型的通用性以及泛化性能都有待提高。本文提出另一種斗桿結構尺寸表達形式，如圖2所示（簡稱“方案二”），結構尺寸變量及取值范圍如表1所示。

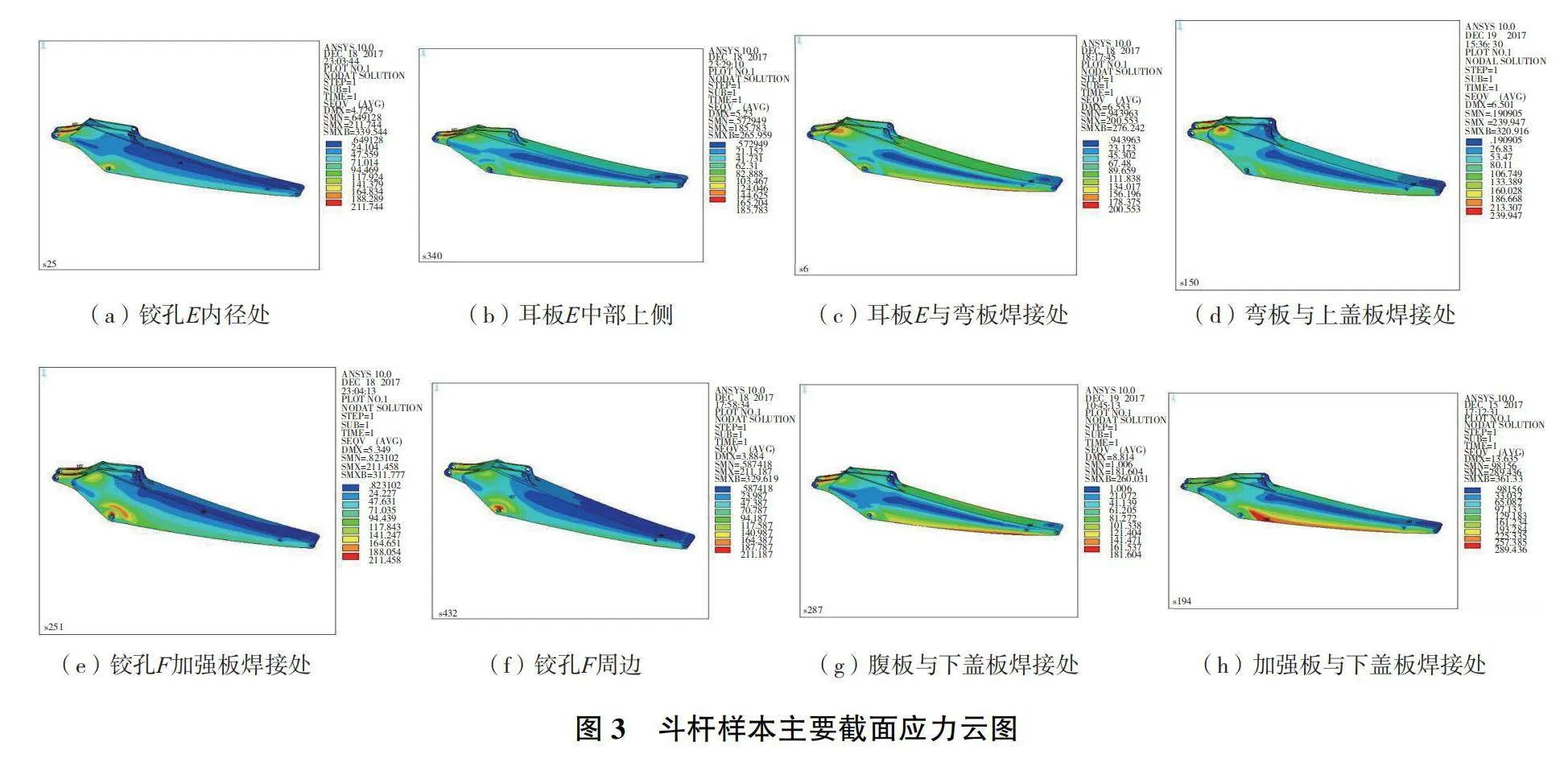
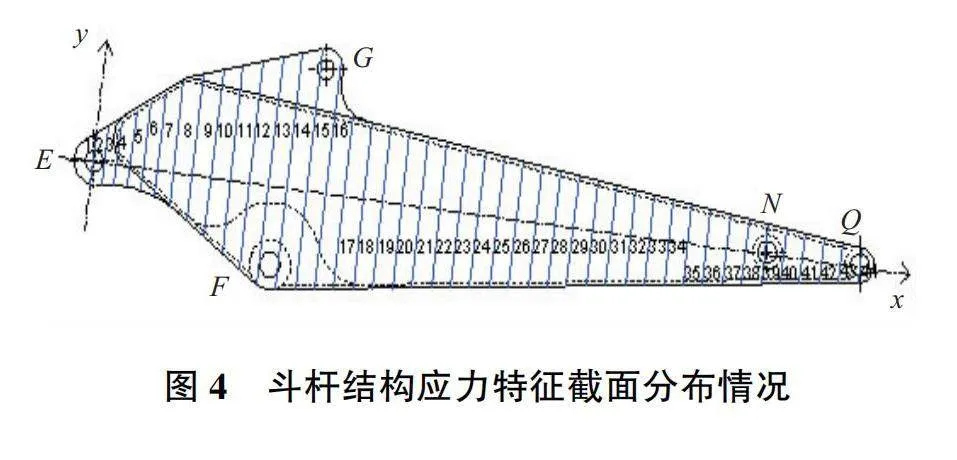
針對圖2所示的斗桿尺寸表達形式，在各尺寸變量取值區間內進行拉丁超立方抽樣，共獲取800組斗桿結構樣本。通過對斗桿結構樣本的應力普查確定不同典型工況下斗桿結構潛在應力危險區域和關鍵區域，如圖3所示。以E、Q兩鉸孔中心的連線EQ為基準，將整個斗桿結構等分為44個垂直于EQ的截面，并對各截面進行編號，如圖4所示。再對所有的樣本進行4個典型工況下各截面應力普查，總結出斗桿結構潛在應力危險區域和關鍵區域主要位置如下：1）斗桿液壓缸耳板鉸孔E內徑處，截面編號1、2；2）斗桿液壓缸耳板上側區域，截面編號3、4所含區域；3）斗桿液壓缸耳板與彎板的焊接位置，即y軸正半軸截面5與y軸負半軸截面8；4）彎板與斗桿上蓋板的焊接處附近區域，即y正半軸截面7、8處；5）鉸孔F內徑與加強板外徑之間，即y負半軸截面11—14；6）鉸孔F處加強板與斗桿下蓋板焊接區，y負半軸截面16、17所含區域；7）鏟斗液壓缸耳板鉸孔G左側區域，y正半軸截面13、14所含區域；8）斗桿結構中部靠前處腹板與下蓋板連接區域，即y負半軸截面34、35；9）連桿鉸孔N附近區域，截面38、39；10）與鏟斗連接鉸孔Q附近區域，截面43。

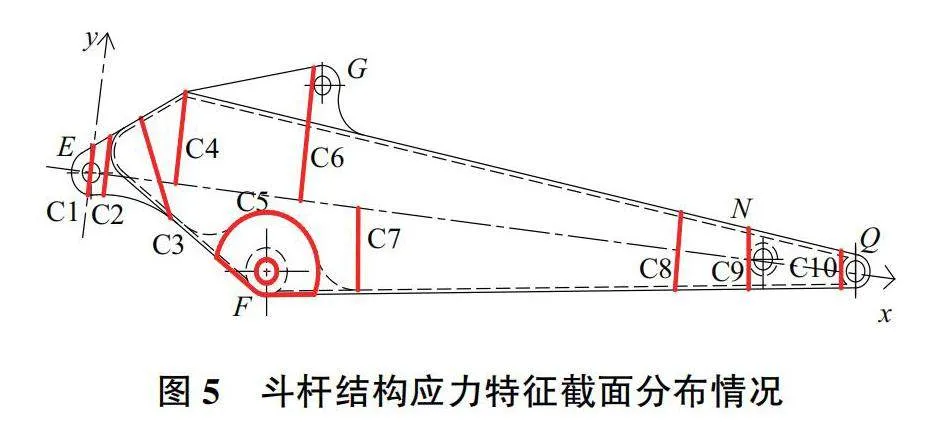
綜上分析可知：潛在危險應力截面主要集中出現在斗桿10個特定區域。這些特定區域設定為10個應力特征截面，如圖5所示。本文建立兩個坐標系用于確定斗桿結構應力特征截面位置，分別為：以E為原點，EQ連線為x軸建立笛卡兒坐標系（命名為E坐標系），對應的應力特征截面為C1、C2、C3、C4、C6、C8，其中應力特征截面C1位于過坐標原點并垂直于x軸；應力特征截面C2位于垂直于x軸且距離原點0.2L_EF·L_FQ/ L_EN；應力特征截面C3位于沿x軸正方向斗桿液壓缸耳板E與彎板上下焊接點的連線位置，截面與x軸交點位置距離原點E為0.45L_EF·L_FQ / L_EN；應力特征截面C4位于垂直于x軸，距離原點0.6L_EF·L_FQ / L_EN的y軸正半軸部分；應力特征截面C6位于垂直于x軸且距離原點（L_EF·L_FQ / L_EN +L_FG·L_GQ / L_FQ -D_G1）/2；應力特征截面C8位于垂直于x軸距離原點0.77L_EN。以F為原點，FQ連線為x軸建立笛卡兒坐標系（命名為F坐標系），對應的應力特征截面為C5、C7、C9、C10，其中應力特征截面C5位于以原點為圓心，以鉸孔F直徑D_F1與側板加強板直徑D_RPF為直徑構成的同心圓；應力特征截面C7位于垂直于x軸距離原點（D_RPF+A_{RC_RPF}） /2；應力特征截面C9位于垂直于x軸距離原點（L_FN·L_FQ / L_EN-D_N2）/2；應力特征截面C10位于垂直于x且與鉸孔Q外徑相切。

2 斗桿結構尺寸參數對應力影響的靈敏度分析

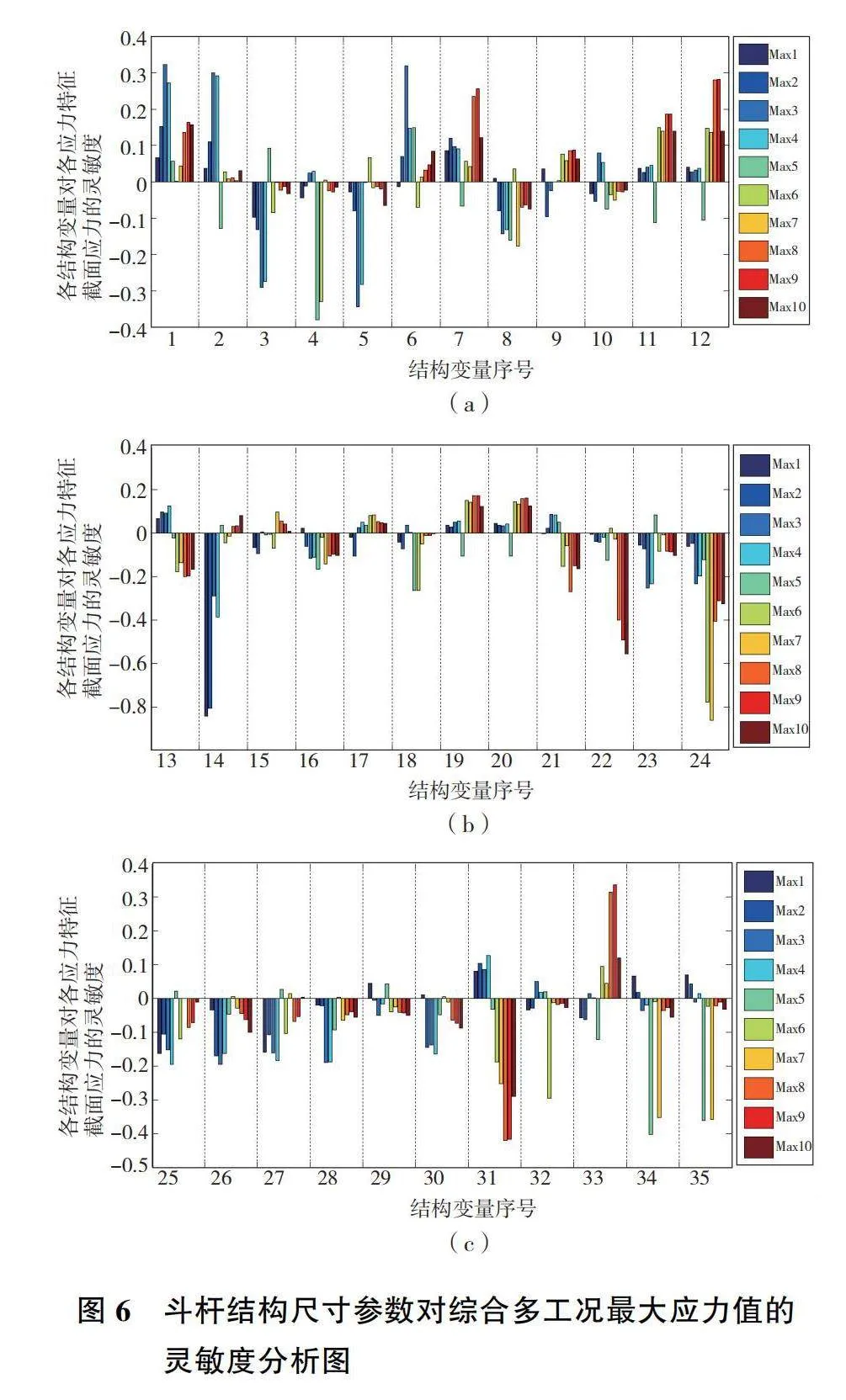
對方案二斗桿結構尺寸表達形式對應的表1所示的35個斗桿結構尺寸參數進行抽樣和參數化建模，并進行典型工況下的自動有限元分析，獲取不同典型工況下斗桿結構各特征截面的最大應力信息。綜合分析典型工況下斗桿結構各尺寸參數對各應力特征截面最大應力值變化影響的敏感度大小，確定斗桿結構各尺寸參數對各應力特征截面應力值大小變化的影響程度，為后期以靈敏度大小為依據選取斗桿結構尺寸參數作為神經網絡應力預測模型的輸入變量而建立的滿足預測精度要求的預測模型提供依據。

本文對所抽取的800組斗桿結構樣本采用基于spearman秩相關分析方法進行斗桿各尺寸參數對各應力特征截面的最大應力值的秩相關分析^[5-6]，斗桿結構尺寸參數對綜合多工況10個應力特征截面最大應力值的靈敏度分析如圖6所示（本刊黑白印刷，相關疑問咨詢作者）。圖中橫坐標1—35表示表1中斗桿結構各尺寸參數編號，縱坐標Max1—Max10代表4個典型工況下每個斗桿結構尺寸參數對斗桿結構10個關鍵應力特征截面最大應力值相應的靈敏度大小。若靈敏度值大于0，則表示該尺寸參數與相應的特征截面最大應力值正相關，且靈敏度值越靠近1則兩者正相關性越強；反之若靈敏度值小于0，則該尺寸參數與相應的特征截面最大應力值為負相關，且靈敏度值越靠近-1則兩者負相關性越強。圖6可知尺寸參數1、2、3、4、5、6、7、12、14、18、21、22、23、24、31、32、33、34、35對相應應力特征截面最大應力值具有較大的相關性，影響靈敏度較大，其靈敏度絕對值均處于0.20～1.00之間。調整這些結構參數可以最大化地影響相應應力特征截面的最大應力值。這些參數與應力特征截面最大應力值相關性很強，其變化能夠直接對相應的應力特征截面應力值產生較大影響。

3 斗桿結構應力神經網絡建模

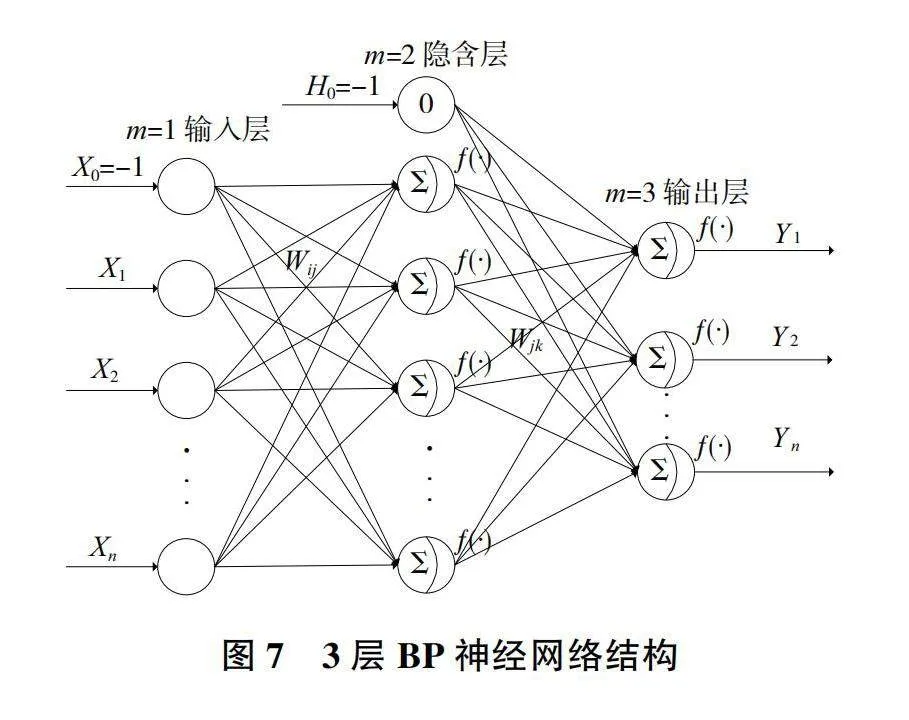
BP神經網絡能夠實現輸入-輸出之間各種復雜非線性關系的映射^[7-8]，本研究以斗桿結構應力特征截面C1—C10的最大應力值作為各個典型工況下所構建的應力神經網絡的輸出變量。中間隱含層神經元個數則根據經驗公式d=I+K+L來確定，其中I和K分別代表輸入層和輸出層神經元個數，L為神經元調節常數，一般取1～10之間，根據經驗公式隱含層神經元個數為15～25個。

分別訓練含有不同隱含層神經元個數的神經網絡模型，以模型訓練總誤差最小的神經網絡模型所含隱含層神經元個數作為該工況下斗桿結構應力神經網絡模型最佳隱含層個數。以工況一為例，該工況下神經網絡模型隱含層個數為22時，其模型訓練總誤差最大為1.365 4，隱含層個數為17時，其模型訓練總誤差最小為0.954 5，故該工況下應力神經網絡模型最佳隱含層個數為17。隱含層神經元作用函數采用對稱型Sigmoid函數，輸出層神經元作用函數采用線性函數，建立3層的BP神經網絡斗桿結構應力預測模型。在不同工況下斗桿結構潛在危險應力截面分布是不一樣的，若只用一個神經網絡結構模型進行不同典型工況下斗桿結構應力特征截面應力值預測，難以達到理想的預測精度。因此，本文針對4種典型工況建立4個斗桿結構應力預測神經網絡模型。為簡化神經網絡模型結構，探究斗桿結構不同輸入變量的選擇對應力預測模型的應力預測精度。根據斗桿結構尺寸參數在不同典型工況下對特征截面最大應力影響的靈敏度分析結果，分別選取斗桿結構靈敏度絕對值在0.20以上的19個斗桿結構尺寸參數為1、2、3、4、5、6、7、12、14、18、21、22、23、24、31、32、33、34、35和靈敏度絕對值在0.18以上的25個斗桿結構尺寸參數為1、2、3、4、5、6、7、11、12、13、14、18、21、22、23、24、25、26、27、28、31、32、33、34、35作為斗桿結構4個典型工況下應力預測模型的輸入變量，建立4個典型工況下斗桿結構神經網絡應力預測模型，如表2所示。通過對兩種不同靈敏度絕對值下所建立的4種典型工況下斗桿結構神經網絡應力預測模型的應力預測誤差的對比，確定4種典型工況下斗桿結構不同輸入變量對神經網絡應力預測模型預測誤差的影響。斗桿結構主要尺寸變量取值范圍如表1所示，該神經網絡結構如圖7所示。

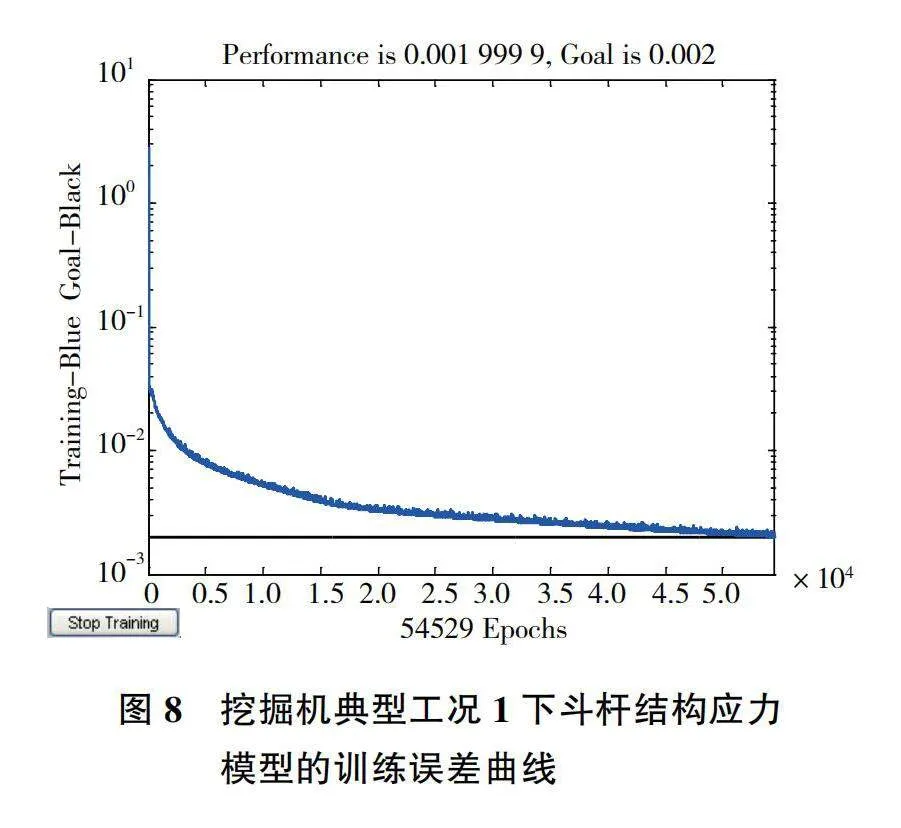
通過對表1所示的斗桿尺寸參數進行拉丁超立方抽樣和參數化建模，并進行典型工況下斗桿結構應力自動有限元分析，獲取4種典型工況下斗桿結構800組樣本作為神經網絡的訓練樣本。利用這些訓練樣本分別對4種典型工況下所建立的4個斗桿結構應力預測神經網絡模型進行訓練。首先分別訓練不同靈敏度下4種典型工況隱含層神經元個數為15～25的神經網絡模型，以神經網絡預測模型輸出的10個特征截面應力值與期望輸出值差值的均方誤差為判斷標準，利用Matlab循環程序依次對該典型工況下含有不同隱含層神經元個數為15～25的神經網絡模型輸出的均方誤差進行對比，取誤差最小的神經網絡模型所含隱含層個數作為該典型工況下斗桿應力特征截面應力值預測模型，確定4種典型工況下神經網絡模型最佳隱含層節，最終以確定的最佳隱含層節點數建立4種典型工況下的斗桿結構神經網絡應力預測模型。以典型工況1下訓練誤差曲線為例如圖8所示。

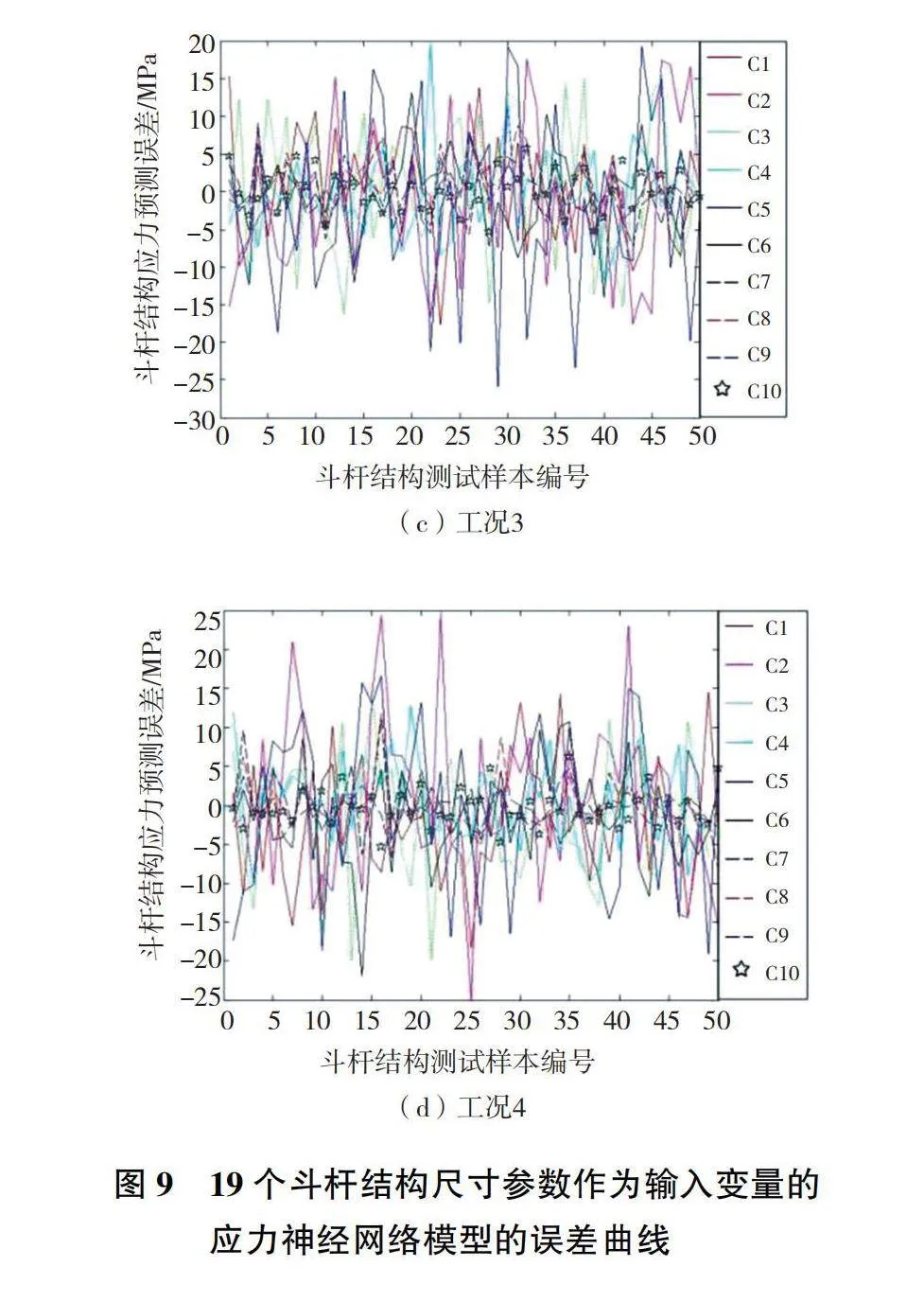
為了驗證所建立的4個典型工況下斗桿結構神經網絡應力預測模型的可行性和預測精度。再重新隨機抽取50組樣本斗桿結構尺寸，利用所建立的CAD/CAE分析模塊對抽取的樣本進行自動有限元分析。對比建立的神經網絡應力預測模型預測的斗桿結構應力值與實際有限元分析應力值差值大小作為預測模型準確性的判斷標準，以檢驗預測模型的正確性。圖9為19個斗桿結構尺寸參數作為輸入變量所構建的斗桿結構神經網絡應力預測模型對應的50個檢測樣本誤差曲線，圖10為25個斗桿結構尺寸參數作為輸入變量所構建的斗桿結構神經網絡應力預測模型對應的50個檢測樣本誤差曲線。

對比圖9和圖10可知：圖9為19個斗桿結構尺寸參數作為輸入變量所構建的斗桿結構神經網絡應力預測模型對應力特征截面C1—C10的應力值，預測誤差在25MPa左右；而圖10為25個斗桿結構尺寸參數作為輸入變量所構建的斗桿結構神經網絡應力預測模型的應力值預測誤差，其值在40MPa左右。結果表明：通過靈敏度分析能夠有效確定合理的斗桿結構尺寸參數作為神經網絡模型輸入變量，所構建的斗桿結構應力預測模型不僅能夠有效簡化神經網絡建模的模型結構，還可以進一步減小應力預測模型的預測誤差。

4 結語

本文通過對斗桿結構應力的神經網絡建模，得到以下結論：

1）通過選取合理的應力特征截面表達斗桿結構在各種典型工況下的應力分布狀態作為神經網絡模型輸出變量，可以有效提高神經網絡模型預測速度，進一步提高應力神經網絡模型預測精度，并實現神經網絡模型在不同類型斗桿結構中的通用性和泛化能力；

2）通過對綜合典型工況下斗桿結構尺寸參數對10個應力特征截面應力值的靈敏度分析，選取與應力特征截面相關性更強的結構尺寸參數作為神經網絡輸入變量，可以有效簡化神經網絡模型結構，進一步提高應力神經網絡模型預測精度；

3）針對不同典型工況下神經網絡結構的建模分析，以樣本訓練總誤差最小確定最佳神經網絡隱含層數目，建立最優應力神經網絡模型，模型預測精度得到有效提高。通過不同結構類型神經網絡模型預測誤差對比分析，應力神經網絡模型預測精度可以達到90％以上。

參考文獻：

[1] LUIGI S. Design of aluminium boom and arm for an excavator[J]. Journal of Terramechanics，2010，47（4）：201-207.

[2] HUAH Y，LIN S W. New knowledge-based genetic algorithm for excavator boom structural optimization[J]. Chinese Journal of Mechanical Engineering，2014，27：392-401.

[3] 楊鐵明.基于知識的綜合多工況挖掘機斗桿結構優化設計關鍵技術研究[D].福州：福州大學，2012.

[4] 張洋梅. 知識引導的挖掘機斗桿結構智能優化設計關鍵技術研究[D].福州：福州大學，2014.

[5] 唐競，宋超，劉夫云，等. 基于結構參數靈敏度分析的商用車駕駛室輕量化方法研究[J]. 機械設計，2021，38（11）：97-101.

[6] 張煥梅，楊瑞剛. 基于響應面法的起重機結構可靠性靈敏度分析[J]. 中國工程機械學報，2020，18（2）： 131-136.

[7] PENG Z S，JI H C，PEI W C，et al. Constitutive relationship of TC4 titanium alloy based on back propagating（BP） neural network（NN）[J]. Metalurgija，2021 （3/4）： 60.

[8] LI Y ， LI J ， HUANG J，et al. Fitting analysis and research of measured data of SAW micro-pressure sensor based on BP neural network[J]. Measurement，2020，155：107533.

收稿日期：2023-01-13