車用鋁合金榫卯結構優化設計

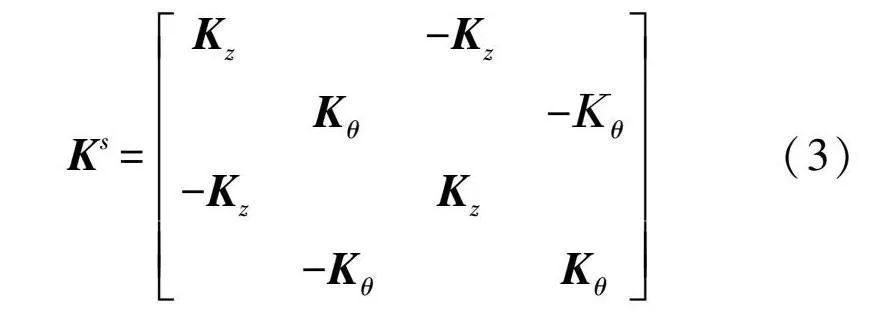
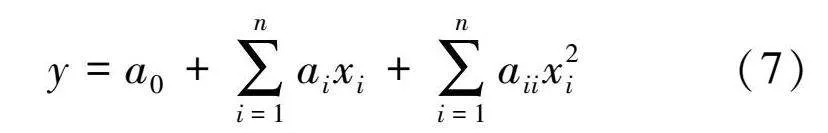
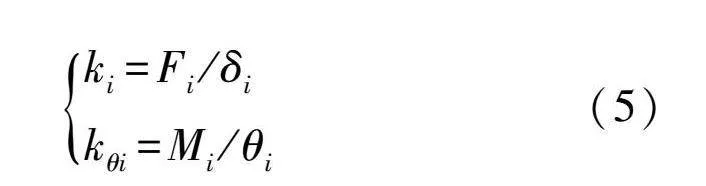
摘"要：根據車用榫卯結構連接的特點，設計一種分析車用榫卯半剛性方法。在汽車車架優化過程中引入彈簧單元，并聯合調用APDL和MATLAB進行二次多項式響應面擬合，將擬合后最大應力與結構質量響應面加權最小作為設計目標，運用線性加權算法獲得滿足工況要求下的最優解。研究表明：車用榫卯優化方案使其最大應力降低10.8%，滿足極限應力約束時車架質量降低6.4%，能量吸收提高7.48%，在提高汽車安全性能的同時實現了輕量化。

關鍵詞：汽車；榫卯；半剛性；響應面

中圖分類號：TH122""文獻標志碼：A""文章編號：1671-5276（2024）02-0011-04

Optimal Design of Automobile Aluminum Alloy Mortise and Tenon Structure

JIANG Yiping1， ZHOU Jinyu2， ZHUANG Bailiang3

（1. School of Mechanical Engineering， Jiangsu University of Technology， Changzhou 213001， China;

2. School of Mechatronics Engineering， Jinling Institute of Technology， Nanjing 211169， China;

3. Jiangsu Branch of China Academy of Machinery Science and Technology Group Co.， Ltd.， Changzhou 213164， China）

Abstract： A semi-rigid method for analyzing mortise and tenon joints was designed according to the characteristics of mortise and tenon joints of vehicles. Spring element was introduced in the optimization process of automobile frame， and the quadratic polynomial response surface was fitted by APDL and MATLAB. The maximum stress and the weight of the response surface of the structure mass after fitting were taken as the design objective， and the optimal solution was obtained by using linear weighting algorithm. The reserch shows that the maximum stress is reduced by 10.8% and the frame mass is reduced by 6.4% and the energy absorption is increased by 7.48% when the ultimate stress constraint is met， which not only improves the safety performance of the vehicle， but also realizes its lightweigt.

Keywords：automobile；mortise and tenon；semi-rigidness；response surface

0"引言

榫卯是古代建筑中柱、梁等構件連接在一起的一種凹凸結合的連接方式。榫卯連接是一種半剛性連接，不但可以承受荷載，而且允許產生一定程度的變形［1］。SOTAYO A 等［2］建立了木結構榫卯連接的半剛性梁單元有限元模型，并用三維實體有限元模型加以驗證。高大峰等［3］采用彈簧單元來模擬箭樓榫卯結構的半剛性，未說明木結構的半剛性單元參數如何實現。方東平等［4］采用非線性接觸分析得到榫卯的半剛性單元參數。隋允康等［5］提出用組合梁單元模擬榫卯的半剛性，采用響應面和優化迭代方法得到組合梁單元參數。

新能源車架連接受古代木結構的啟發，將榫卯作為車架梁柱之間的連接形式，解決了鋁合金采用傳統電阻點焊技術難以實現可靠連接的問題。王念等［6］應用APDL對不同橫截面的鋼鋁混合骨架結構進行工況分析，但沒有考慮榫卯結構的半剛性。XIONG H Y等［7］建立混合梁單元模型模擬車架鋁合金榫卯節點結構的半剛性，同時對比分析實體模型的彎矩-扭轉曲線和混合梁單元的彎矩-扭轉曲線說明混合梁單元的計算速率高于實體單元，而有限元分析中只應用梁單元不能全面反映出鋁合金榫卯的實際狀況［8］。因此在鋁合金榫卯采用實體單元和梁單元組合建模，既可反映結構連接的實際情況，又可提高計算效率。

目前汽車鋁合金車架輕量化研究側重于參數輕量化，如熊會元等［9］利用響應面和多目標遺傳算法對榫卯截面特征參數進行優化，在保證車架強度要求的基礎上實現輕量化目標。何坤等［10］對車用鋁合金榫卯的外框厚度、肋板厚度和立柱的長寬進行優化，在滿足靜剛度的要求下有效地實現輕量化。這些車架輕量化研究未考慮半剛性特性，不能準確反映力學內涵，通常很難獲得較正確的最優解。為了精確模擬榫卯的半剛性特性，在車架有限元系模型的連接關系中添加彈簧單元，聯合調用APDL和MATLAB構建車架響應面，運用線性加權法對汽車鋁合金榫卯車架結構進行優化研究。

1"鋁合金榫卯有限元分析

1.1"鋁合金榫卯三維模型

空心擠壓鋁型材因質量輕且能構成榫卯結構保證汽車車身有較好的綜合性能，在電動汽車車身被廣泛應用。本文采用中巴客車后橋及側圍骨架使用率較高的 6061-T6 鋁合金十字榫卯結構作為研究對象，如圖1所示。鋁合金榫卯結構主要由兩部分組成，即立柱和橫梁。在裝配過程中，橫梁支撐筋與立柱左右面采用過盈配合，根據GB/T 5371—2004選擇過盈量為0.045mm。

1.2"鋁合金榫卯單元模型

復雜結構會根據需要采用不同的單元類型模擬不同的結構部位，以精確掌握節點的變形情況。鋁合金榫卯應用于汽車車架連接中，在實際工程中單一單元很難完全模擬整個結構的受力狀態，需采用適合構件結構行為的單元模擬。

榫卯接觸部分用CONTA174覆蓋在橫梁內表面，CONTA174可用來表示目標面和接觸面之間滑移和摩擦因數，TARGE170覆蓋在立柱表面，組成三維接觸對，而構成接觸對的接觸單元和目標單元通過共享實常數組聯系在一起，可精確反映橫梁和立柱之間的過盈配合。

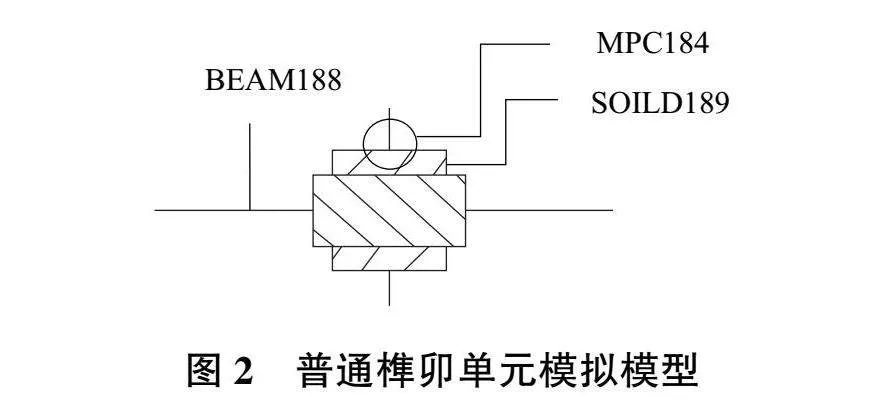
橫梁和立柱具有不規則截面，在連接范圍內用四面體單元SOLID189模擬，其余部分用梁單元BEAM188模擬可縮短單元數量。在提高仿真效率同時準確反映橫梁與立柱之間的變形情況。兩個單元連接部用多點約束單元MPC184實現梁單元和實體單元配合［11］。榫卯單元模型如圖2所示。

1.3"有限元方程模型

利用結構力學的平衡條件和邊界條件把各個單元按原來的結構重新連接起來，形成整體的有限元方程［12］。

F=KU（1）

式中：K為剛度矩陣；U為位移矩陣；F為載荷矩陣。

由式（1）推導出結構的剛度矩陣

U=K-1F（2）

依據式（2）計算出鋁合金榫卯的位移矩陣為U=［0 0.068 0.040 0 0.068 0.040］T，與文獻［7］的實驗位移數據相差24.4%。

依據式（2）可推位移的差別是由于剛度矩陣存在誤差，表明現有的有限元分析方法存在誤差。在有限元分析中添加適當的剛度矩陣能準確體現榫卯的特性。

2"鋁合金榫卯半剛性特性分析

2.1"半剛性特性

鋁合金榫卯結構在載荷作用下因過盈配合的存在而產生相對轉動，即為介于剛性連接和鉸鏈連接的半剛性連接。

在有限元仿真中，常用虛擬彈簧單元來模擬榫卯半剛性連接。虛擬彈簧單元Combin39無質量無尺寸，將其設在立柱和橫梁連接處以模擬榫卯連接特性，彈簧單元節點自由度與其連接的構件單元自由度數相同，相當于在原有的接頭處加入了拉壓彈簧和彎扭彈簧。隨著彈簧剛度的變化，節點的結構力學性能亦發生變化，能夠較為實際地模擬榫卯結構特性，其剛度矩陣為

Ks=Kz－KzKθ－Κθ－KzKz－KθKθ（3）

式中：Kz為軸向剛度；Kθ為彎曲剛度。計算公式為

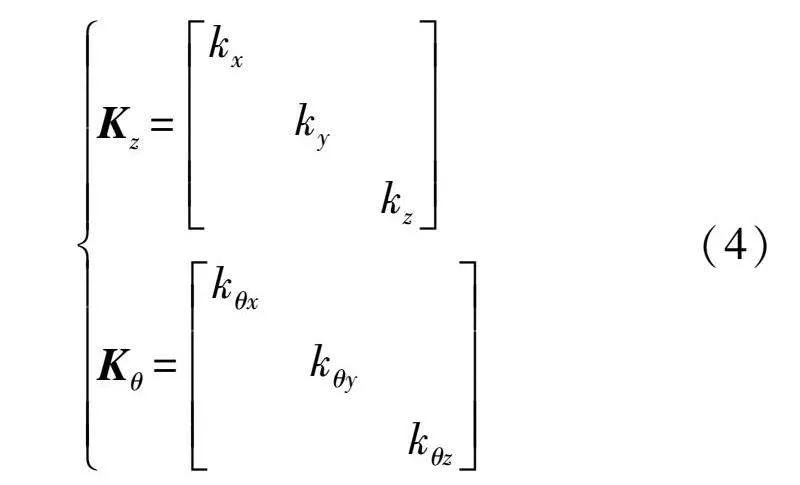
Kz=kxkykz

Kθ=kθxkθykθz（4）

式中：kx、ky、kz分別為x、y、z軸的軸向剛度；kθx、kθy、kθz分別為繞x、y、z軸的彎曲剛度。公式分別如下：

ki=Fi/δikθi=Mi/θi（5）

式中：Fi為節點在x、y、z軸方向的受力；δi為節點在x、y、z軸方向的位移；Mi為節點繞x、y、z軸方向的轉矩；θi為節點繞x、y、z軸方向的轉角。

根據模型的受力情況，鋁合金榫卯在y、z軸方向的抗壓能力相同，不同方向的抗彎能力相同，即簡化為：ky=kz=k1，kθx=kθy=kθz=k2，由此Ks值取決于k1、k2 兩個剛度參數值。

2.2"壓力-位移分析

依據式（2）計算出添加虛擬彈簧單元的鋁合金榫卯在三點彎曲下的位移為U=［0 0.10 0.06 0 0.10 0.06］T，與文獻［7］中實驗數據所轉換的U相差4.5%，提高了添加虛擬彈簧單元下的位移準確度。

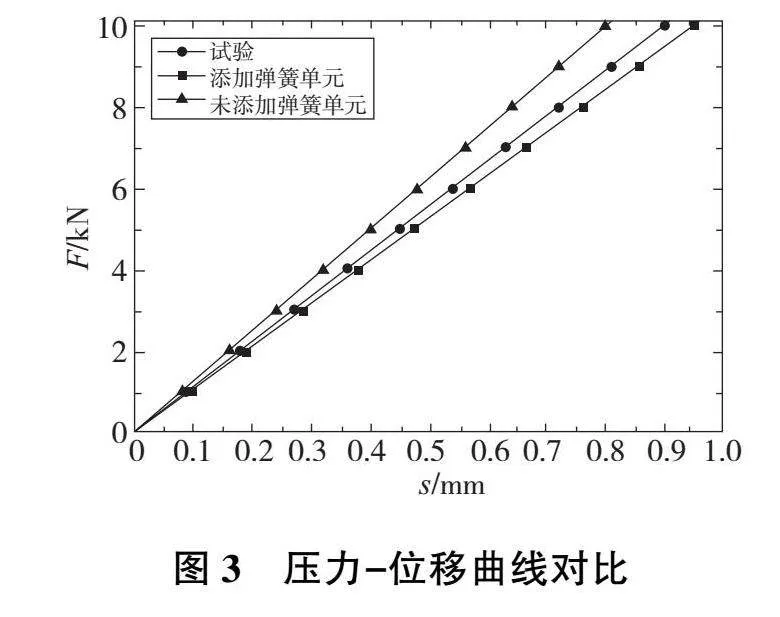
聯合調用MATLAB和ANSYS輸出鋁合金榫卯在不同單元的壓力-位移曲線，與文獻［7］中的試驗曲線相比較，發現混合單元曲線與實驗曲線相近。這一現象與理論分析結果相似，表明混合單元的鋁合金榫卯有限元分析的精確性。壓力-位移曲線對比如圖3所示。

3"汽車車架優化設計

為提高車架輕量化分析的精確度，在車架優化中通過在十字榫卯節點增加彈簧單元來考慮結構的半剛性特性，運用APDL進行工況分析（側向承受1kN壓力），再運用MATLAB進行響應面擬合，最后應用線性加權法得到車架輕量化的最優解。

3.1"設計變量

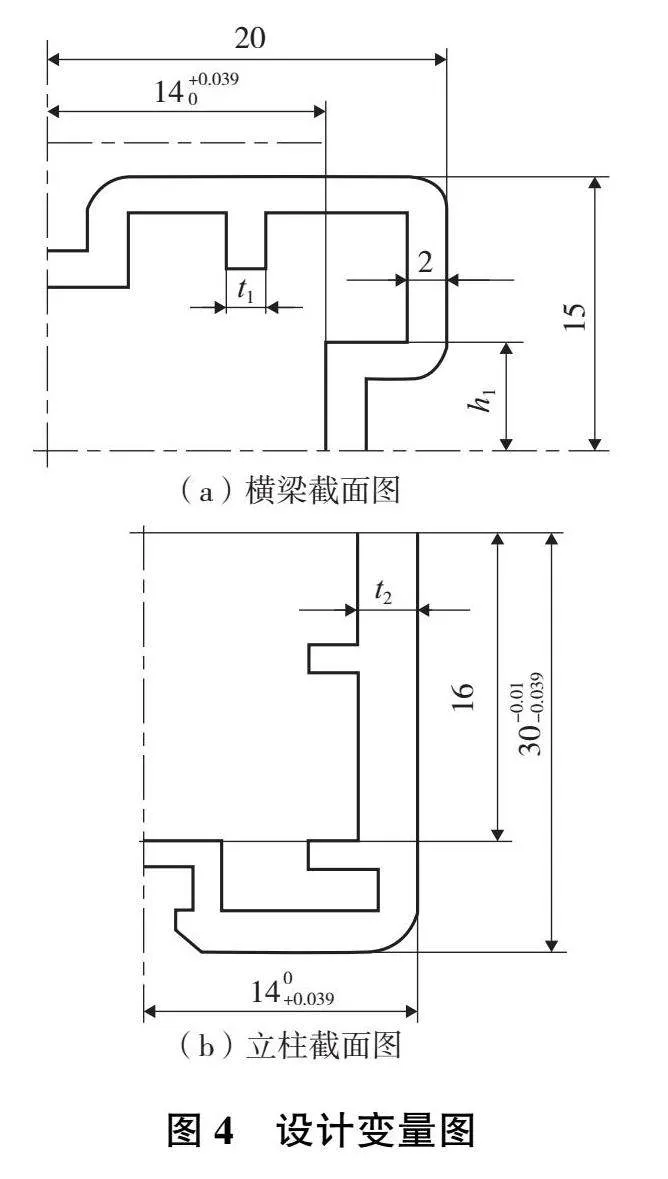
在保證車架整體外圍尺寸不改變的前提下，選擇橫梁厚度t1、支撐筋高度h1、立柱厚度t2、配合間隙e等作為車架結構優化設計變量，其設計變量如圖4所示。

3.2"優化模型

車架結構優化旨在車架達到安全性能要求的同時，使其質量盡量小。車架以車架的極限應力作為約束條件，以結構質量和最大應力的加權最小為目標函數，建立優化模型為

findX=（x1x2x3x4）

minf（X）=μm（X）+（1－μ）fσ（X）

s.t.fσ（X）≤［σ］，x4≤0.3（6）

式中：x1為橫梁厚度；x2為支撐架高度；x3為立柱厚度；x4為過盈量；μ為歸一化系數；m（X）為車架質量響應面；fσ（X）為車架最大應力響應面；［σ］為鋁合金的極限屈服應力，［σ］=345MPa；find表示最優解；min表示目標函數為最小；s.t.表示約束條件。

3.3"響應面

為清晰反映設計變量與最大壓力和質量之間的關系，采用響應面進行構建兩者之間的非線性關系。響應面是利用有限的樣本點擬合出一個簡單響應函數來等效真實的輸出函數。響應面可節省有限元抽樣計算的時間，提高計算效率。車架最大應力或質量與設計變量之間的函數關系為

y=a0+∑ni=1aixi+∑ni=1aiix2i（7）

式中：y為車架的最大應力或質量；a0、ai和aii為響應面方程待定系數；n為設計變量的個數；xi為設計變量。

3.4"結果分析

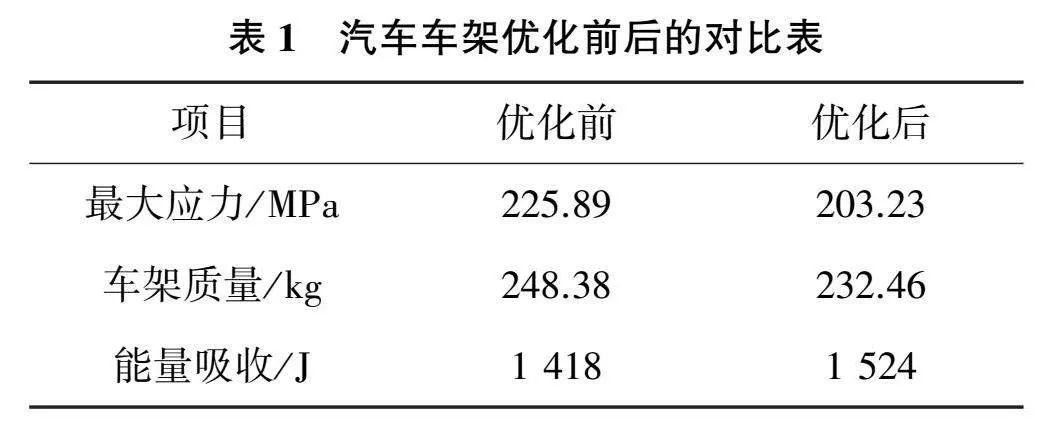
運用線性加權法優化的最優解為橫梁厚度1.76mm，支撐筋高度7.87mm和立柱厚度3.12mm，配合間隙0.21mm。汽車車架優化前后的對比如表1所示。

由表1可知，優化后車架最大應力由225.89 MPa減少到203.23MPa，降低了10.03%；車架能量吸收由1 418J增加到1 524J，增加了7.48%，提高了汽車的安全性能。車架在優化前的質量為248.38kg，優化榫卯的截面尺寸后，其質量為232.46kg，經過優化后的車架質量減少了15.92kg，降低了6.4%，車架的減重效果明顯。綜上所述，優化后的汽車提高了性能，實現了輕量化。

4"結語

在創建榫卯有限元分析模型中通過添加彈簧單元正確體現半剛性特性，并應用到汽車車架上進行優化研究，結論如下：

1）將實體單元和梁單元結合應用于榫卯單元，提高計算效率和仿真的準確性；

2）在立柱和橫梁接觸處添加彈簧單元，準確體現了鋁合金榫卯結構的半剛性，提高了后續研究的準確性；

3）通過對多目標優化結果和優化前進行對比分析，結果表明優化后的汽車車架在工況下的最大應力降低10.03%，能量吸收提高7.48%，提高了汽車行駛的安全性。車架質量降低6.4%，有助于提高汽車的續航里程。

參考文獻：

［1］ 武國芳，孫競成，黃成建，等. 中國傳統木結構榫卯連接節點力學性能研究進展［J］. 林業工程學報，2020，5（4）：29-37.

［2］ SOTAYO A，GREEN S，TURVEY G. Experimental and Finite Element （FE） modelling of timber fencing for benchmarking novel composite fencing［J］. Composite Structures，2016，158：44-55.

［3］ 高大峰，曹鵬男，丁新建. 中國古建筑簡化分析研究［J］. 地震工程與工程振動，2011，31（2）：175-181.

［4］ 方東平，俞茂鋐，宮本裕，等. 木結構古建筑結構特性的計算研究［J］. 工程力學，2001，18（1）：137-144.

［5］ 隋允康，常婧雅，葉紅玲. 木結構半剛性結點的數值模擬［J］. 北京工業大學學報，2011，37（9）：1298-1303.

［6］ 王念，高群，黃心深，等. 輕型電動客車榫卯結構骨架仿真分析［J］. 機械設計與制造，2015（5）：181-184，188.

［7］ XIONG H Y， TAN Z R， ZHANG R H， et al. Numerical calculation model performance analysis for aluminum alloy mortise-and-tenon structural joints used in electric vehicles［J］. Composites Part B：Engineering，2019，161：77-86.

［8］ 杜寶江，陳長松，吳恩啟，等. 基于ANSYS梁單元與實體單元的組合建模研究［J］. 機械設計與研究，2013，29（4）：61-63.

［9］ 熊會元，羅志鵬，黃心深，等. 中巴車鋁合金立柱截面多目標優化［J］. 機械設計與制造，2019（1）：158-161.

［10］ 何坤， 劉強. 基于HyperWorks的車用鋁合金榫卯結構優化［C］// 2017Altair技術大會論文集， 南京：［s.n］，2017： 459-465.

［11］ 王新敏，李義強，許宏偉. ANSYS結構分析單元與應用［M］. 北京：人民交通出版社，2011.

［12］ LIU Q， WANG J S， HUANG X S， et al. In-plane and out-of-plane bending responses of aluminum mortise-tenon joints in lightweight electric vehicle inspired by timber structures［J］. Thin-Walled Structures，2018，127：169-179.

收稿日期：20230407