側風作用下不同裝載敞車氣動性能研究

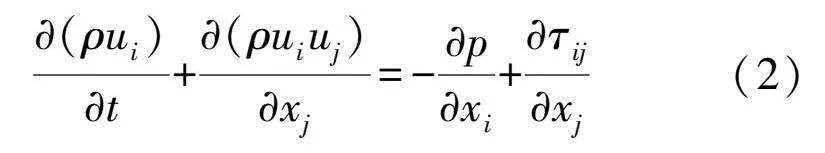
摘"要：針對不同裝載情況的敞車，開展敞車在空載、半載、滿載3種情況下氣動性能的研究。研究結果表明：單節敞車氣動力的變化規律與整車氣動力的變化規律一致；空載敞車所受的氣動阻力最大，半載敞車次之，滿載敞車最小；滿載敞車所受的氣動升力最大，半載敞車次之，空載敞車最小；3種敞車所受的側向力非常接近，最大差距僅為1.9％；空載敞車和半載敞車所受的氣動力較為接近，而滿載敞車與前兩種車型有明顯差距。

關鍵詞：鐵路貨運列車；裝載；敞車；氣動性能；數值模擬

中圖分類號：U272""文獻標志碼：A""文章編號：1671-5276（2024）02-0025-04

Study on Aerodynamic Performance of Gondola Cars with Different Loadings under Crosswind

XIE Yujiang， WU Zhenfeng

（School of Mechanical Engineering，Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract：According to the different loading conditions of gondola car， the aerodynamic performance of the gondola car under three conditions of empty-load， half-load and full-load was studied. The reserch results show that the change law of the aerodynamic force of a single gondola car is consistent with that of the whole vehicle， the aerodynamic drag of empty-load train is the largest， followed by half-load train， and full-load train is the least. The aerodynamic lift force of full-load train is the largest， half-load train comes to the second， and empty-load train is the least. The lateral forces of the three trains are very close with the biggest difference as merely 1.9%. The aerodynamic force of empty-load and half-load gondola car is relatively close， while full-load gondola car has a significant gap with the former two models.

Keywords：railway freight train; load; gondola car; aerodynamic performance; numerical simulation

0"引言

蘭新鐵路是我國貨物運輸的重要通道，由于特殊的地理位置，蘭新鐵路經過了多個風區，這些風區環境惡劣，常年伴有強烈側風，對我國貨運列車的安全運行帶來了威脅。針對側風作用下貨運列車的氣動性能，國內外的眾多學者主要作了以下研究。梁習鋒等［1］基于二維、非定常N-S方程，忽略車輛的轉向架，研究了側風作用下敞車、棚車、罐車和客車的氣動性能。周丹等［2］基于三維、非定常N-S方程，研究了側風作用下不同類型鐵路貨車在5m路堤上運行時的氣動性能。何華等［3］基于二維、定常N-S方程，忽略了車輛的轉向架，研究了側風作用下導流板對敞車氣動性能的影響，并對敞車周圍的流場進行了分析。金琦、熊小慧等［4-5］基于三維、定常N-S方程，研究了側風作用下篷布對敞車氣動性能的影響。HASSAN H等［6］使用大渦模擬法研究了側風作用下貨運列車的氣動性能，得到了機車和集裝箱貨車周圍的壓力、流場分布以及相關的氣動參數。

敞車是我國目前應用數量最多、范圍最廣的鐵路貨車，占總體鐵路貨車數量的50％以上，具有非常高的研究價值。雖然有學者研究了側風作用下敞車的氣動性能，但這些研究或忽略了敞車的轉向架，或僅僅基于二維條件，對三維條件下帶有完整轉向架的敞車研究不足。敞車結構特殊，內部具有巨大的空腔，這就導致了敞車在空載和載物狀態下的外形有所不同。敞車在運輸煤炭、道碴等物品時存在裝不滿的情況，由于這些物品呈顆粒狀，裝在一起時表面縫隙較小，故這種狀態下的敞車可以近似看做空腔裝滿一半物品的半載狀態；而敞車在運輸鋼材、機械設備等畏雨物品時通常會蓋篷布，由于本文主要考慮敞車的氣動特性，并不涉及流固耦合問題，故這種狀態下的敞車可以近似看做空腔裝滿物品的滿載狀態。因此本文針對側風條件，對敞車在空載、半載、滿載3種情況下的氣動性能進行了研究。

1"研究方法

1.1"控制方程

連續性方程、動量守恒方程和能量守恒方程是控制流體流動的基本方程。本文列車的運行速度為120km/h，側風速度為24.5m/s，馬赫數小于0.3，空氣不可壓縮。不可壓縮流之間的熱量交換很小，故本文不考慮能量守恒方程。對于恒定流，在不考慮流體壓縮性情況下的連續性方程為

（ρuj）xj=0（1）

式中：ρ表示流體密度；xj（j=1，2，3）表示直角坐標系的坐標分量；uj（j=1，2，3） 表示直角坐標系中速度矢量u沿xj方向的分量。動量方程為

（ρui）t+（ρuiuj）xj=－pxi+τijxj（2）

式中：p表示作用在流體微元體上的壓強；τij表示因分子黏性而產生的作用在微元體的黏性應力張量。

計算流體力學可以較為準確地模擬湍流流動，本文利用軟件Fluent進行數值模擬。湍流模型選用SST k-ω模型，其優點是內存消耗低、精度較高、容易收斂，比較適合近壁自由流動問題。為保證計算結果的準確性，采用SIMPLE算法求解雷諾平均N-S方程，并用二階迎風格式對其進行離散。

1.2"幾何模型和網格劃分

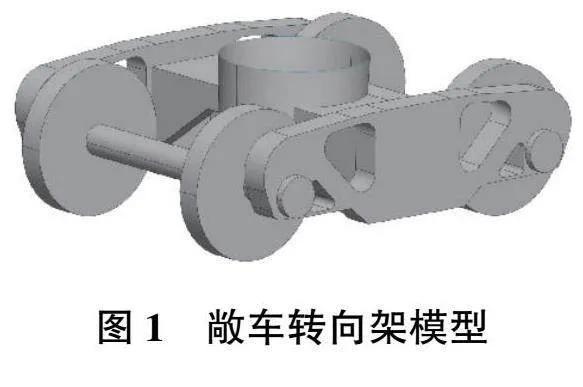
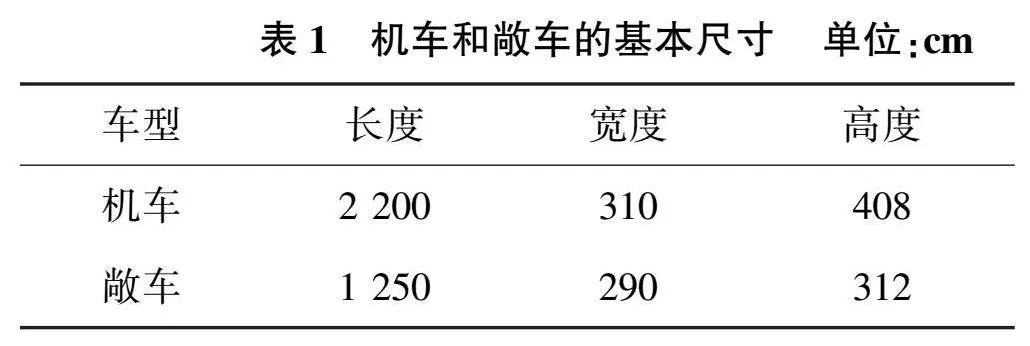
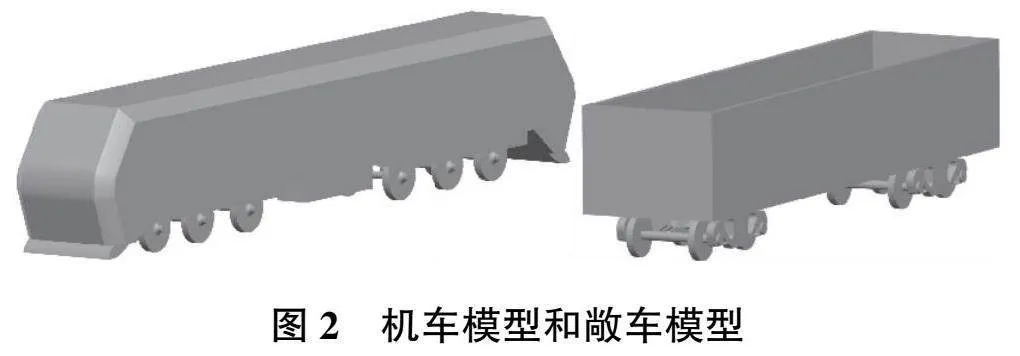
選取國內某型電力機車分別牽引空載敞車、半載敞車、滿載敞車作為研究對象，對機車的車窗、車燈、轉向架進行了適當的簡化；忽略了受電弓、雨刮器、門把手。參照車鉤的基本信息，用長寬高分別為40cm、20cm、16cm的長方體代替車鉤［7］。敞車轉向架模型如圖1所示，機車模型和敞車模型如圖2所示，機車和敞車的基本尺寸如表1所示。

312

網格質量對仿真計算收斂性及結果準確性至關重要［8］。由于貨運列車外形復雜，故利用Workbench-meshing進行非結構網格劃分，然后用Fluent-meshing將非結構網格轉化為多面體網格。計算域共設有2層加密區，對車體表面、轉向架等區域進行了局部加密，邊界層共設有12層，第1層邊界層網格厚度的y+值控制在30～100，計算域的非結構網格數量在2 000萬左右，轉化為多面體網格后在400萬左右。列車及地面網格如圖3所示。

1.3"計算工況

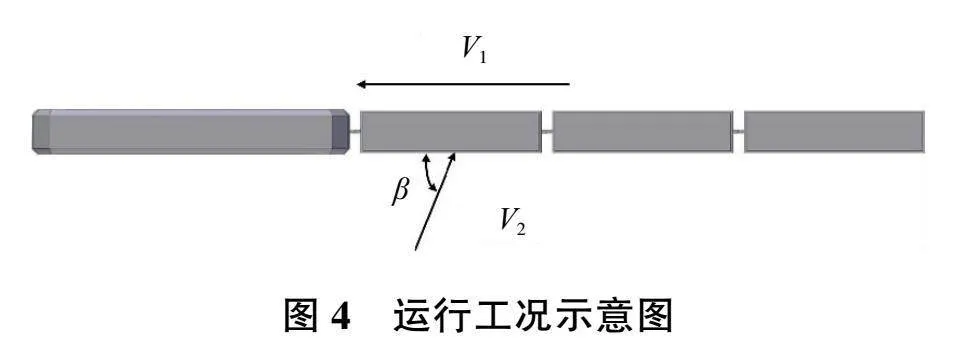
目前有兩種方式可以模擬側風作用下貨運列車的運行，一種是動網格法，另一種是合成風法［9］。本文選用合成風法，列車運行速度V1設置為120km/h，側風速度V2設置為24.5m/s（10級風），側風角β設置為60°，運行工況示意圖如圖4所示。

1.4"計算域和邊界條件

計算域和邊界條件的設置是數值模擬的關鍵，參照列車空氣動力學性能數值仿真規范，對計算域的大小和邊界條件進行了合理的設置［10］。列車計算域為長方體，地面設置為與列車運行速度大小相等，方向相反的滑移壁面；頂面設置為對稱邊界；車體表面設置為無滑移壁面，計算域入口條件為速度入口，出口條件為壓力出口，遠場壓力為標準大氣壓。模型計算域的大小如圖5所示，其中L表示列車長度。

1.5"方法可行性驗證

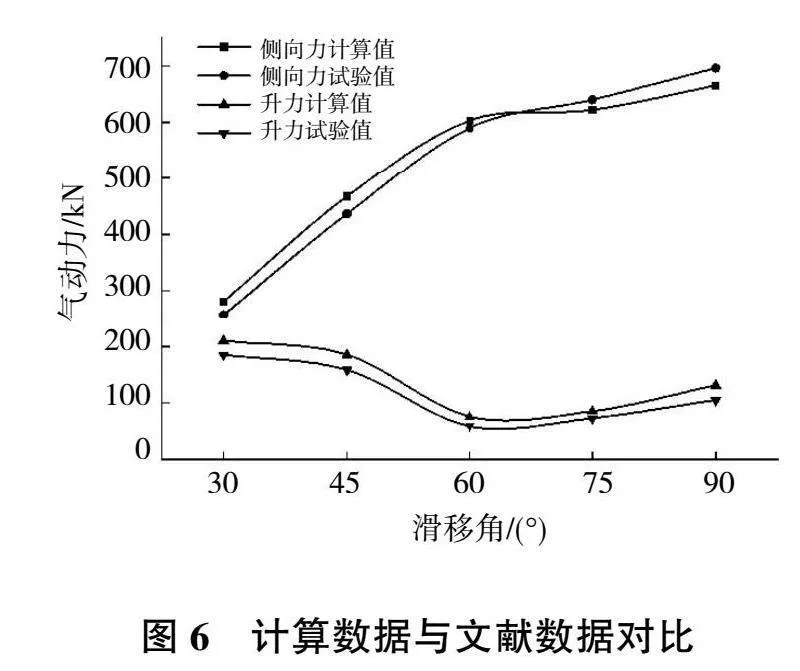
為驗證本文所采用方法的正確性，參考中南大學團隊利用風洞試驗所測得的數據進行可行性驗證。風洞試驗的列車為1節機車牽引3節棚車，路堤高度為5m，來流速度為60m/s，側滑角分別為30°、45°、60°、75°、90°。計算數據與文獻中風洞實驗的數據對比如圖6所示。

從圖6可以看出，計算所得到的側向力及升力和文獻試驗結果規律一致，吻合性較好，因此認為本文所采用的模型和數值計算方法是合理的。

2"計算結果與討論

2.1"氣動力分析

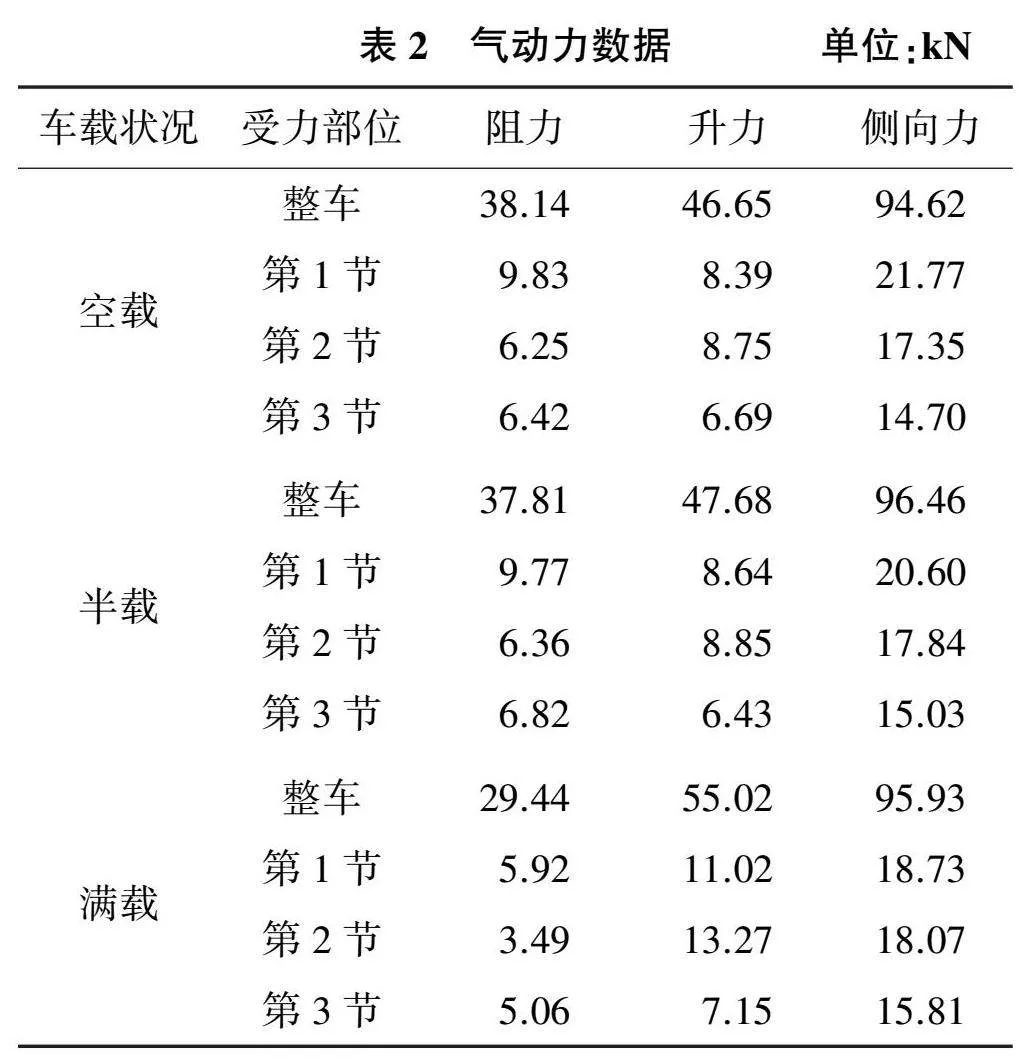
側風作用下，機車牽引3節空載敞車、半載敞車、滿載敞車所受的氣動力如表2所示。

從表2可以看出，空載敞車所受的氣動阻力最大，半載敞車次之，滿載敞車所受的氣動阻力最小。其中空載敞車和半載敞車差距較小，差距僅為0.8％；空載敞車和滿載敞車差距較大，差距可達29.6％。滿載敞車所受的氣動升力最大，半載敞車次之，空載敞車最小。其中空載敞車和半載敞車差距較小，差距僅為2.2％；空載敞車和滿載敞車差距較大，差距可達17.9％。3種敞車所受的側向力非常接近，最大差距僅為1.9％。無論是空載、半載還是滿載，每節敞車氣動力的變化規律一致。對于同一種敞車而言，第1節車所受的氣動阻力最大，第3節車次之，第2節車最小；第2節車所受的氣動升力最大，第1節車次之，第3節車最小；第1節車所受的側向力最大，第2節車次之，第3節車最小。值得注意的是，單節敞車氣動力的變化規律與整車氣動力的變化規律一致，空載敞車和半載敞車所受的氣動力較為接近，而滿載敞車與前兩種車型有明顯差距。

2.2"壓力流場分析

為分析3種敞車的阻力變化情況，選擇前后都是相同車型的第2節車進行研究，第2節敞車的頭尾部表面壓力如圖7所示。

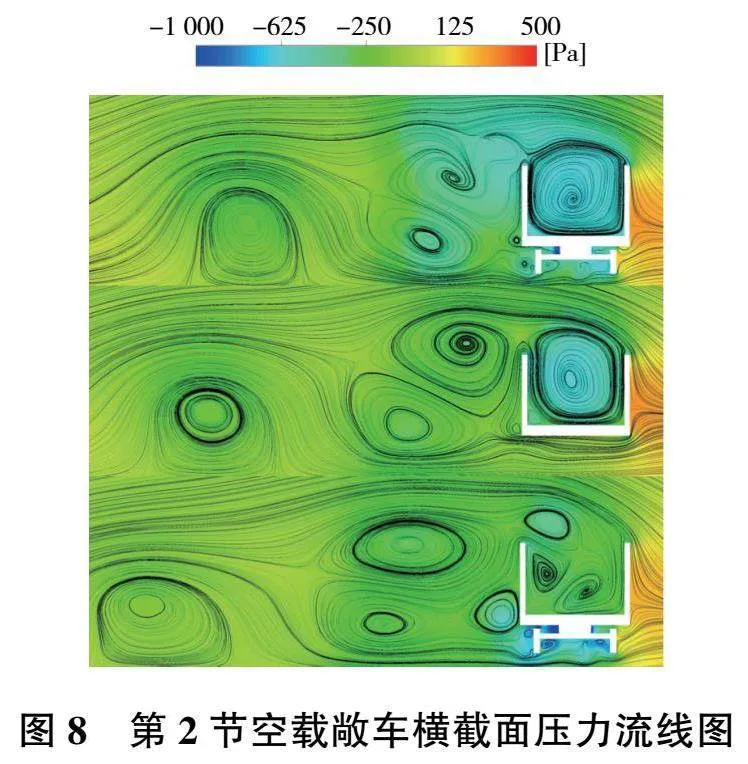
從圖7可以看出，空載敞車和半載敞車的頭尾部壓力分布非常相似，這是空載敞車和半載敞車所受氣動阻力非常接近的原因。雖然滿載敞車與前2種車的頭部壓力分布較為相似，但滿載敞車尾部所受的負壓明顯小于前2種車，因此滿載敞車的壓差小于前兩種車。這是滿載敞車所受氣動阻力最小的原因。為分析同種敞車所受升力和側向力的變化情況，選擇敞車的3種典型橫截面進行研究，第2節空載敞車的前輪、中間、后輪橫截面壓力流線圖如圖8所示。

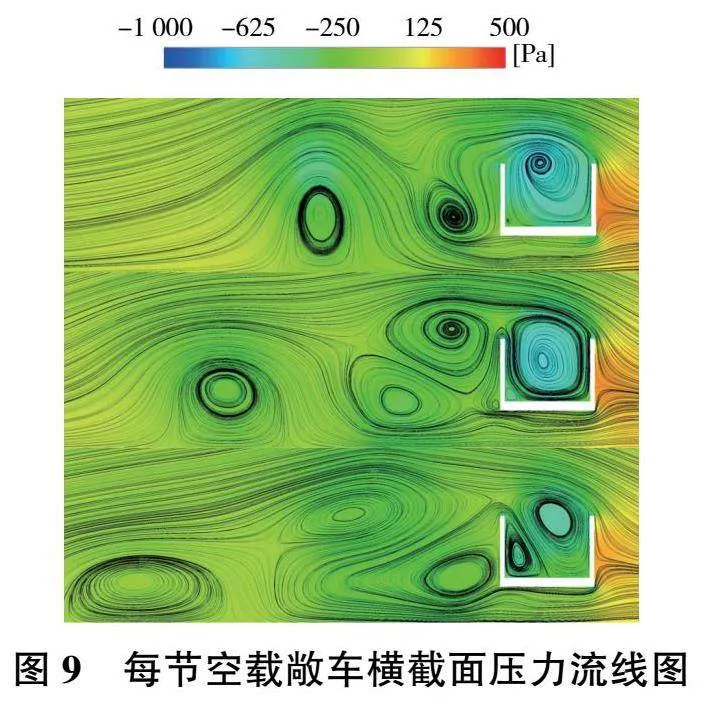
從圖8可以看出，3種位置下的空載敞車左側都有一個較大的漩渦，且此漩渦隨著截面位置向后移動而向敞車左側移動。前輪截面和中間截面的漩渦分布非常類似，敞車空腔內都有一個較大的漩渦，而后輪截面的漩渦分布則有所不同，敞車空腔內較大的漩渦分離成3個較小的漩渦。產生這種現象的原因是空氣流速的不同，空氣流速快的地方壓力小，這也是前輪和中間截面空腔內的負壓明顯大于后輪截面的原因。為進一步分析同種敞車所受升力和側向力的變化情況，選擇流場變化最為穩定的敞車中間橫截面進行分析，每節空載敞車中間截面壓力流線圖如圖9所示。

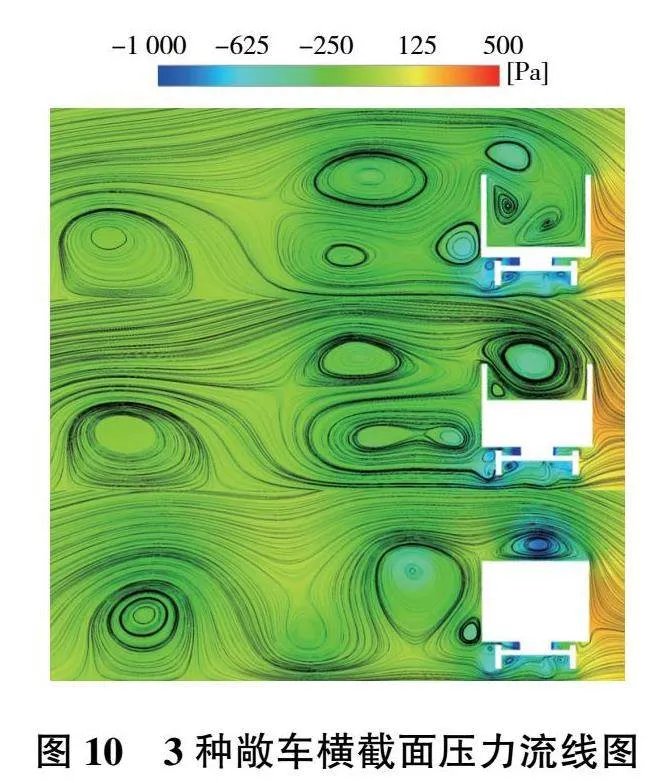
從圖9可以看出，隨著位置向后移動，敞車迎風側的正壓會減小，最左側的漩渦也會向左移動，這是第1節車側向力最大，第2節車次之，第3節車最小的原因。第3節敞車空腔內的負壓明顯小于前2節車，這是第3節車升力最小的原因。與圖8對比可知，第3節敞車空腔內的漩渦也發生了分離。為進一步分析不同類型敞車所受升力和側向力的變化情況，選擇流場變化最為明顯的敞車后輪橫截面進行分析，3種敞車的第2節敞車后輪橫截面壓力流線圖如圖10所示。

從圖10可以看出，3種敞車的流場差異非常大。3種敞車頂部漩渦的大小和數量都有所不同，這也導致了頂部壓力有所不同，滿載敞車頂部的負壓明顯較大，而半載和空載敞車的頂部壓力則較為接近，這也是滿載列車所受的升力最大，半載和空載列車所受的升力差距僅為2.2％的原因。值得注意的是，靠近3種敞車左側的漩渦數量都是3個，只是大小和位置的不同，3種敞車兩側的壓力分布非常相似，這是3種類型列車側向力都非常接近的原因。

3"結語

本文針對不同裝載情況下的敞車，開展了敞車在空載、半載、滿載3種情況下氣動性能的研究。采用SIMPLE算法求解雷諾平均N-S方程，湍流模型采用SST k-ω模型。研究結果表明：空載敞車所受的氣動阻力最大，半載敞車次之，滿載敞車所受的氣動阻力最小；滿載敞車所受的氣動升力最大，半載敞車次之，空載敞車最小；3種敞車所受的側向力非常接近，最大差距僅為1.9％；對于同一種車型而言，每節車所受的氣動力也有所不同；單節敞車氣動力的變化規律與整車氣動力的變化規律一致，空載敞車和半載敞車所受的氣動力較為接近，而滿載敞車所受的氣動力與前2種車型有明顯差距。此研究結果可為貨運列車的安全運行提供參考。

參考文獻：

［1］ 梁習鋒，熊小慧. 4種車型橫向氣動性能分析與比較［J］. 中南大學學報（自然科學版），2006，37（3）：607-612.

［2］ 周丹，田紅旗，楊明智，等. 強側風作用下不同類型鐵路貨車在青藏線路堤上運行時的氣動性能比較［J］. 鐵道學報，2007，29（5）：32-36.

［3］ 何華，田紅旗，熊小慧，等. 橫風作用下敞車的氣動性能研究［J］. 中國鐵道科學，2006，27（3）：73-78.

［4］ 金琦，梁習鋒，熊小慧. 橫風對篷布氣動升力的影響［J］. 鐵道科學與工程學報，2010，7（4）：96-100.

［5］ 熊小慧，梁習鋒，金琦. 橫風作用下鐵路貨車篷布氣動力數值模擬計算［J］. 中南大學學報（自然科學版），2015，46（2）：728-735.

［6］ HASSAN H， CHRIS B. Large-eddy simulation of the flow around a freight wagon subjected to a crosswind［J］. Computers amp; Fluids，2010，39（10）：1944-1956.

［7］ 趙懷瑞. 車輛工程導論［M］. 北京：中國鐵道出版社，2015.

［8］ 李田，秦登，安超，等. 計算網格對列車空氣動力學不確定性的影響［J］. 西南交通大學學報，2019，54（4）：816-822.

［9］ PREMOLI A，ROCCHI D，SCHITO P，et al. Comparison between steady and moving railway vehicles subjected to crosswind by CFD analysis［J］. Journal of Wind Engineering and Industrial Aerodynamics，2016，156：29-40.

［10］ TB/T 3503.4—2018鐵路應用空氣動力學 第4部分：列車空氣動力學性能數值仿真規范［S］.

收稿日期：20221010