基于時頻相干函數的多跨梁損傷識別方法

摘"要：為解決連續小波變換損傷識別方法受邊界和約束干擾的問題，提出一種基于時頻相干函數的結構損傷識別方法。該方法通過時頻相干函數構造損傷識別指標對多跨梁進行損傷識別，能夠有效降低邊界和約束對損傷識別的干擾，提高損傷的定位精度。通過對梁模型的數值仿真分析與實驗驗證，結果表明：通過時頻相干函數構造的損傷指標，有效地消除了連續小波變換所帶來的邊界效應和約束的影響，能夠實現對多跨梁損傷的準確定位，且在噪聲干擾下依然具有良好的損傷定位能力。

關鍵詞：損傷識別；時頻相干函數；連續小波變換

中圖分類號：U441+.4;U448.21+7""文獻標志碼：A""文章編號：1671-5276（2024）02-0101-05

Multi-span Beam Damage Detection Method Based on Time Frequency Coherence Function

ZHANG Zhe， MIAO Bingrong， HU Tianqi， CHEN Hui， ZHANG Ying， ZHAO Langtao

（ State Key Laboratory of Traction Power，Southwest Jiaotong University，Chengdu 610031，China）

Abstract：A damage detection method based on the time frequency coherence function is proposed to address the continuous wavelet-based damage detection methods distorted by border and constrain distortion. With the proposed method， the damage detection on muti-span beam is realized based on time frequency coherence function， which can significantly reduce the distortion of damage detection caused by border and constrain and upgrade dasmage positioning accuracy. The results of numerical investigation and experimental verification on beam show that the proposed method can effectively eliminate the effect of border and constrain due to continuous wavelet transform， accurately position multi-span damage even under noise interference.

Keywords：damage detection; time frequency coherence function; continuous wavelet transform

0"引言

機械結構和土木結構在實際使用工況中不可避免的會產生損傷，損傷的產生和發展可能會對結構的性能、安全性、可靠性和使用壽命產生不利影響。為了防止結構失效并保證結構的安全性，及時地發現損傷并對結構進行維修是十分重要的。結構健康監測（structural health monitoring， SHM）是一種測量結構當前狀態的有效方法，其中結構損傷識別是健康監測的核心部分。

可以通過對比結構在損傷前后模態參數的變化，如固有頻率、模態振型和阻尼比的變化對結構的損傷進行識別［1］，但由于結構的固有頻率及模態振型在損傷前后的變化較小，使用固有頻率、模態振型等進行損傷識別的方法在損傷定位中存在精度不高的共性問題和局限性，人們開始關注與能量概念相關的其他模態方法［2］。連續小波變換方法被廣泛使用在結構損傷識別中，該方法通過將信號變換到尺度域中，能夠放大信號中的奇異值與不連續點［3］。在損傷位置處小波變換系數會出現明顯的極值，根據該極值的位置可以很好地識別信號的奇異點并確定損傷位置。

KATUNIN A［4］分析了測量環境、噪聲、小波選擇、損傷位置和邊界效應對損傷識別效果的影響。單純的連續小波變換方法存在無法量化損傷和邊界效應等不足，常將連續小波變換和其他技術結合，提高損傷識別的效果。SHA G G等［5］在小波變換的基礎上結合Teager能量算子（teager energy operator， TEO）對振型進行處理，通過融合TEO-WT振型對尺度的積分構建了損傷指標，并通過數值仿真和試驗驗證了該指標對多損傷復合梁的識別效果，管德清等［6］將連續小波變換與神經網絡結合，使用應變模態小波模極大值定位損傷并以此作為神經網絡的輸入，實現了對損傷的定位和量化。還可以考慮將連續小波變換與相干性結合，在連續小波變換基礎之上，計算有損和無損結構振型小波變換系數的相干性進行損傷識別。ZUMPANO G ［7］通過計算超聲波信號的時頻相干函數，實現了對軌道損傷的識別，且有效地避免了邊界反射對識別效果的影響。ZHENG H［8］使用譜相干處理加速度信號和聲發射信號，根據接收信號與已知的特定信號的相干程度能夠判斷軌道、車輪和軸承的損傷。

通過連續小波變換識別損傷時，結構邊界和約束處的振型突變會導致小波系數產生局部極值影響損傷識別的效果。為解決此問題，本文擬將連續小波變換與時頻相干函數結合構造損傷指標，旨在降低邊界和約束對損傷識別的影響，提高多跨梁損傷定位的精度。

1"理論背景

1.1"連續小波變換

對于任意函數f（x）∈L2（R），其連續小波變換定義為

f（x）ψ*a，b（t）dx（1）

式中：ψ*為小波母函數的復共軛；b為平移因子；a為尺度因子。從定義可以看出連續小波變換是時間參數b和尺度參數a的函數，通過小波變換，可以同時在時間和頻率域上觀察信號。

不同小波函數對損傷有不同的識別效果。參考小波函數的選擇原則［9-10］，考慮支撐長度、消失矩和正交性等因素，本文選擇“gaus4”小波對多跨梁的振型進行小波分析。

1.2"時頻相干函數

信號s1（t）和s2（t）的時頻相干函數為：

CoH（t，f）=R12（t，f）2R11（t，f）R22（t，f）（2）

其中：

Rij（t，f）=∫TW*i（τ，f）Wj（τ，f）dτ（3）

式中：Wi（τ，f）和Wj（τ，f）分別為第i個和第j個信號的連續小波變換；時間積分窗T=［t－Δt，t+Δt］。時頻相干函數可以表示兩個信號在時頻域上的相關程度，損傷位置處的有損結構和無損結構響應相關程度會降低。

1.3"基于時頻域相干的損傷指標

假設u（x）和d（x）分別為有損結構和無損結構的振型向量，根據式（3）可知u（x）和d（x）的時頻相干函數為：

Rij（x，s）=∫L0W*i（u，s）Wj（u，s）du（4）

CoH（x，s）=Rud（x，s）2Ruu（x，s）Rdd（x，s）（5）

式中：W為連續小波變換；L為結構的長度；下標u和d分別代表無損結構和有損結構。

對式（5）取倒數：

CoH（x，s）=1/CoH（x，s）（6）

考慮結構的m階振型，認為固有頻率變化更大的模態，對應的振型變化也更明顯。為了提高指標的靈敏度，根據各階固有頻率的差異對振型的時頻相干函數進行融合［11］，得到

CoH（x，s）=∑mi=1CoHi（x，s）×1－ωiuωid2（7）

式中：CoHi表示通過第i階振型計算得到的時頻相干函數；ωiu和ωid分別表示連續梁的第i階無損和有損固有頻率。

構建損傷指標時，為了減小尺度選擇對損傷識別效果的影響，在尺度方向對時頻相干函數進行積分：

p（u）=∫s1s0CoH（x，s）ds（8）

式中s1和s0為尺度參數的上下限，本文中選取的尺度積分范圍為［0.1， 10］。

使用Z-score對p（u）標準化，并設定閾值對較小的峰值進行濾除：

Z-score=p－mean（p）SD（p）（9）

式中mean（p）和SD（p）分別為p的均值和方差。最終將損傷指標DI定義為：

DI=Z-score，Z-score≥0

0，Z-score＜0（10）

1.4"損傷識別流程

本文以多跨梁結構作為研究對象，基于模態參數，利用時頻相干函數構造損傷指標對結構進行損傷識別。具體步驟如下。

步驟1：建立多跨梁結構的有損與無損有限元模型。考慮邊界約束條件，通過模態分析得到結構的固有頻率和振型。

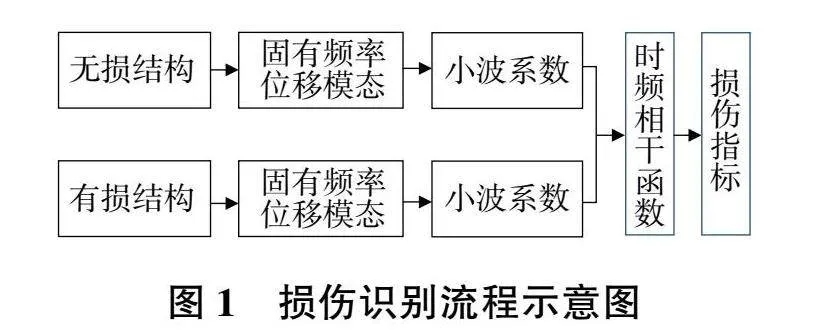
步驟2：對振型進行3次樣條插值。對有損和無損結構的振型分別進行連續小波變換，并基于小波系數計算時頻相干函數，然后對時頻相干函數進行歸一化并將各階模態下的時頻相干函數進行融合，對尺度進行積分構造相干損傷指標，圖1為損傷識別流程示意圖。

步驟3：根據設定的閾值，判定出損傷單元的位置。

2"數值算例

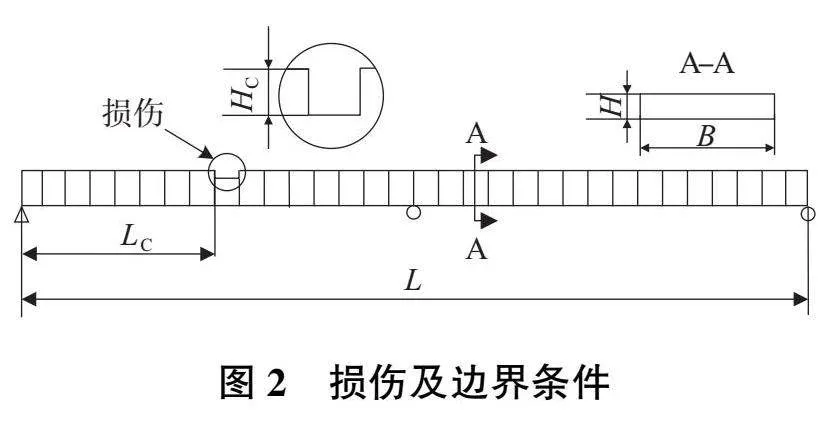
以連續梁結構作為研究對象進行損傷識別算法的研究。建立連續梁有限元模型尺寸：L×B×H為1 200×60×4，mm；彈性模量E=2.1 GPa；泊松比ν=0.3；密度ρ=7.8×103kg/m3。沿長度方向劃分為24個單元，單元尺寸為50 mm，損傷及邊界條件如圖2所示。

圖2中Hc為損傷的深度，采用損傷深度與截面厚度的比值Hc/H來表征單元處的損傷程度，通過改變梁單元的截面尺寸在有限元模型中添加不同程度的損傷。

為了探究該方法在不同工況下對不同大小和位置處的損傷識別效果，在有限元模型中設置了3種工況類型的損傷，損傷工況設置參數如表1所示。

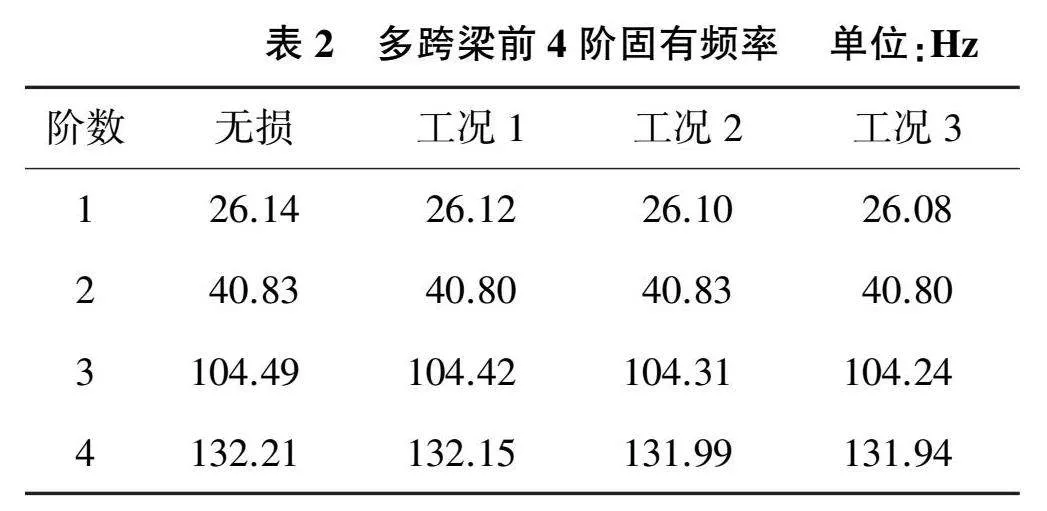
本文選擇多跨梁的前4階模態參數進行損傷識別的研究。通過有限元建模與模態分析，獲得結構的前4階模態振型和頻率并對振型進行3次樣條插值。不同工況下，多跨梁前4階固有頻率如表2所示。

2.1"單損傷識別

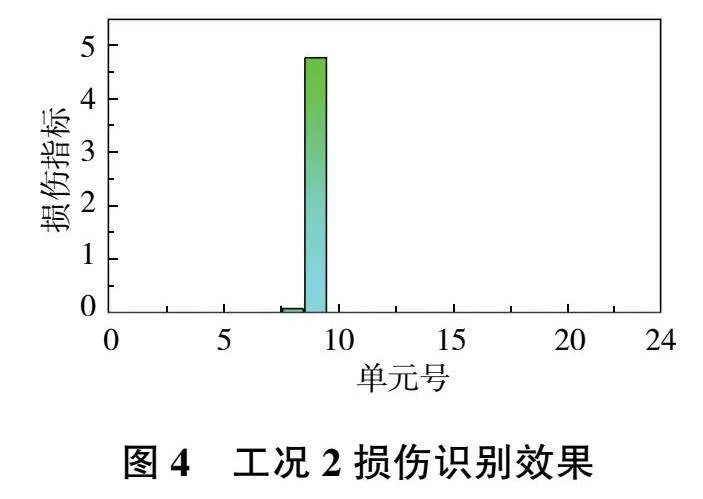
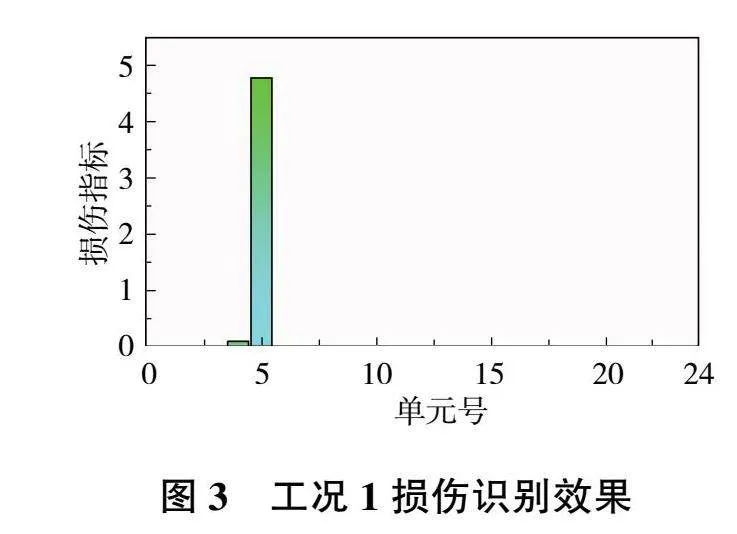
為了驗證本文提出的基于時頻相干函數方法對損傷識別的有效性，分別在多跨梁第5號和第9號單元處設置了單損傷。在工況1和工況2下，損傷指標的識別效果如圖3和圖4所示。

從圖3和圖4中可以看出，在單損傷工況下，由時頻相干函數構建的損傷指標可以準確地對損傷進行定位。同時，在邊界處，該損傷指標并未因受到邊界效應的干擾而出現誤判，具有較高的損傷識別準確度。

2.2"多損傷識別

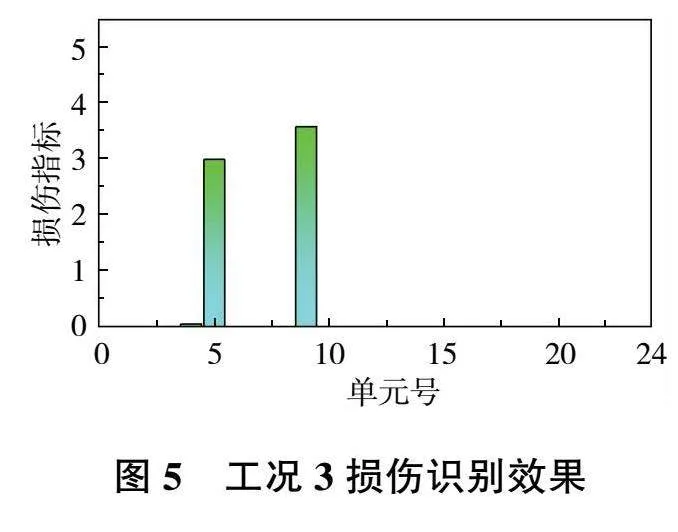
為了研究該方法對多損傷的識別能力，在多跨梁同一跨內的5號和9號單元設置了2個損傷程度分別為5%和10%的損傷。工況3下，損傷指標的識別效果如圖5所示。

從圖5中可以看到，該損傷指標同樣可以對兩處損傷準確定位，同時在邊界處未發生誤判的情況。雖然在損傷位置附近損傷指標出現了不為0的情況，但其值遠小于損傷位置處損傷指標的值，所以對損傷識別的準確性不會造成影響。同時可以發現，該損傷指標在結構存在多個損傷時，其值的大小可以反映出損傷的相對大小。

2.3"抗噪性分析

在實際的結構模態試驗中，不可避免地受到環境、測量和系統噪聲的影響。為了研究損傷指標在噪聲環境下的可靠性，在各階模態振型中添加一定的噪聲水平，噪聲水平通過信噪比SNR（dB）表示：

SNR=10lgPsPn（11）

式中：SNR為信噪比水平；Ps和Pn分別為信號和噪聲的功率，通過下式對振型添加噪聲：

n=+randn×P10SNR/10（12）

式中：和n分別為原始振型信號和添加噪聲后的振型信號；P為振型信號的功率；SNR為添加的噪聲水平，dB；randn是均值為0，標準差為1的標準正態分布隨機向量。

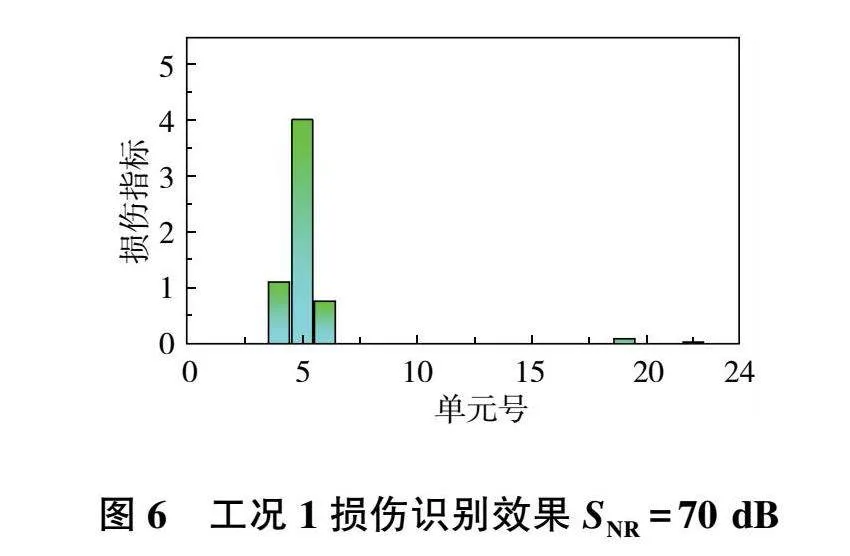
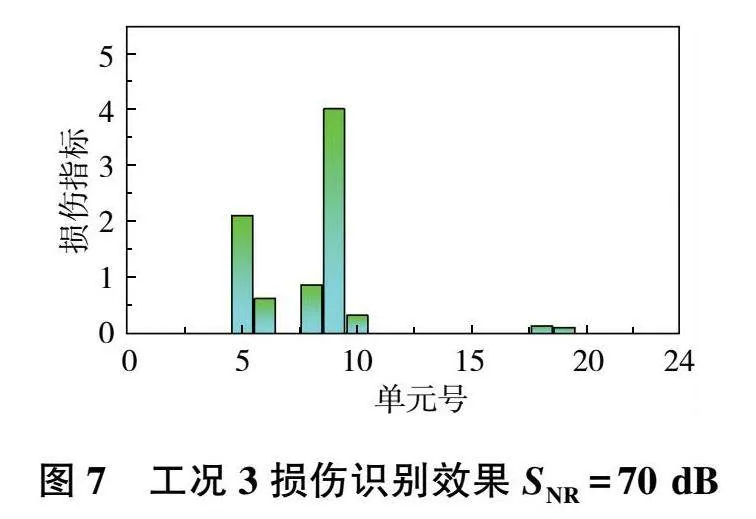
為了探究構建的損傷指標在噪聲環境下的損傷識別效果，在單損傷工況1和多損傷工況3位移模態中加入信噪比水平為70 dB的高斯白噪聲，對應的識別效果如圖6和圖7所示。

從圖6和圖7中可以看到信噪比水平在70 dB時，在無損傷位置處損傷指標受到了一定的干擾，但可以看到損傷單元處的損傷指標明顯較大，依然可以準確地定位損傷。由于相鄰的單元間存在公共的節點，損傷單元的相鄰單元更容易出現干擾。

3"試驗驗證

為了驗證該方法的可靠性，使用與仿真一致的梁結構驗證損傷識別的效果，梁的尺寸L×B×H為1 200×60×4，mm。通過缺口的形式在梁的8號單元和19號單元處加工出兩處損傷。

模態試驗采用DH5923N信號采集儀、1個加速度傳感器和力錘進行各測點振動響應數據的采集，試驗現場如圖8所示。

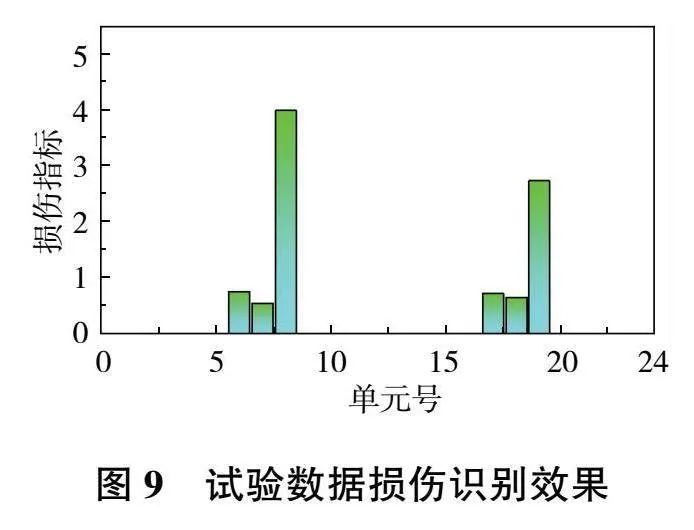
將梁分為49個測點，即采樣間隔為25mm。在采集系統中計算并輸出結構的前4階模態振型。對試驗模態振型進行3次樣條插值，然后進行連續小波變換，計算時頻相干損傷指標，識別效果如圖9所示。

從圖9可以看到，對于實測數據，在16號單元處存在一定的干擾，但依然可以判斷出8號單元和19號單元為損傷單元，且8號單元和19號單元處的損傷指標值大于其他單元，說明該損傷指標能對損傷進行定位。

4"結語

針對連續小波損傷識別方法受到邊界與約束影響的問題，本文在連續小波變換的基礎上，研究時頻相干函數對多跨梁結構損傷的識別效果及其抗噪性，得到以下結論：

1）該損傷指標可以對多跨梁的單損傷和多損傷進行定位，且在SNR=70 dB的噪聲水平下依然具有定位損傷的能力；

2）通過時頻相干函數構造的損傷指標，有效地消除了連續小波變換所帶來的邊界效應影響；

3）該方法需要精確地估計結構的模態，對于復雜結構的識別效果，還需要進一步試驗研究。

參考文獻：

［1］ AVCI O， ABDELJABER O， KIRANYAZ S， et al. A review of vibration-based damage detection in civil structures：from traditional methods to machine learning and deep learning applications［J］. Mechanical Systems and Signal Processing，2021，147：107077.

［2］ 繆炳榮，劉俊利，張盈，等. 軌道車輛結構振動損傷識別技術綜述［J］. 交通運輸工程學報，2021，21（1）：338-357.

［3］ SAADATMORAD M， JAFARI-TALOOKOLAEI R A， PASHAEI M H， et al. Damage detection on rectangular laminated composite plates using wavelet based convolutional neural network technique［J］. Composite Structures，2021，278：114656.

［4］ KATUNIN A. Nondestructive damage assessment of composite structures based on wavelet analysis of modal curvatures：state-of-the-art review and description of wavelet-based damage assessment benchmark［J］. Shock and Vibration，2015，2015：1-19.

［5］ SHA G G， RADZIENSKI M， SOMAN R， et al. Multiple damage detection in laminated composite beams by data fusion of Teager energy operator-wavelet transform mode shapes［J］. Composite Structures，2020，235：111798.

［6］ 管德清，廖俊文. 連續梁結構損傷識別的小波神經網絡方法研究［J］. 中外公路，2016，36（1）：136-139.

［7］ ZUMPANO G， MEO M. A new damage detection technique based on wave propagation for rails［J］. International Journal of Solids and Structures，2006，43（5）：1023-1046.

［8］ ZHENG H. Integrated railway remote condition monitoring［D］. Birmingham，West Midlands，UK：University of Birmingham，2017.

［9］ DOUKA E， LOUTRIDIS S，TROCHIDIS A. Crack identification in beams using wavelet analysis［J］. International Journal of Solids and Structures，2003，40（13/14）：3557-3569.

［10］ GENTILE A， MESSINA A. On the continuous wavelet transforms applied to discrete vibrational data for detecting open cracks in damaged beams［J］. International Journal of Solids and Structures，2003，40（2）：295-315.

［11］ SERRA R，LOPEZ L. Damage detection methodology on beam-like structures based on combined modal wavelet transform strategy［J］. Mechanics amp; Industry，2017，18（8）：807.

收稿日期：20221024