基于改進GWO?GM（1，1）模型的直流充電樁在線計量誤差預測方法研究

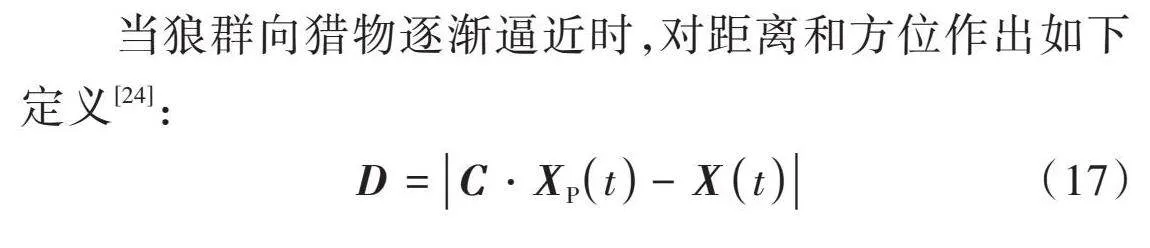
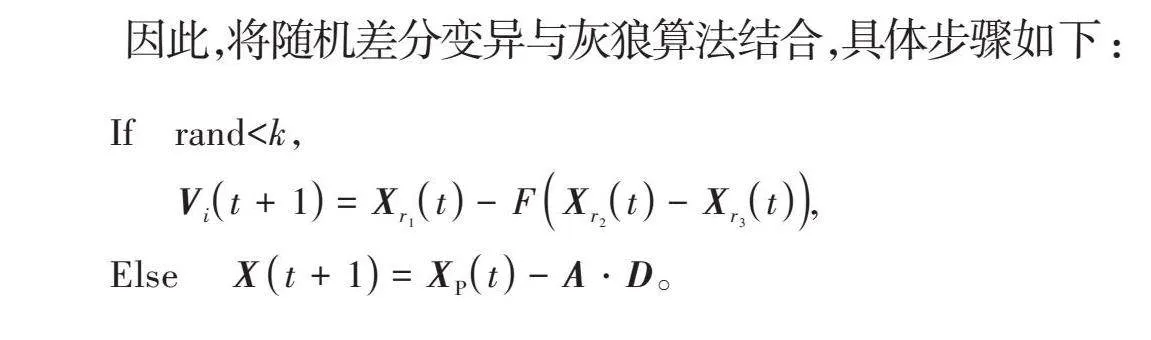
摘" 要： 針對傳統灰色理論預測精度不高和基本的灰狼算法容易陷入局部最優的情況，提出改進的灰狼算法與灰色理論融合的直流充電樁在線計量誤差預測模型。首先，通過差分變異策略進行向量合成，引入非線性變異概率[k]，增強前期全局搜索能力，平衡灰狼算法的全局和局部搜索能力，避免陷入局部最優的問題；然后，將改進的算法應用于GM（1，1）模型，通過多次迭代尋找適應度值最好的一組灰狼位置，尋找到最優背景值對灰色模型進行優化，進一步提高模型的預測精度；最后，將改進前與改進后的驗證模型進行對比，改進的灰色預測模型相較于基礎的灰色模型均方誤差與平均絕對誤差分別降低了70.7%和27.2%，驗證了所提方法的有效性。

關鍵詞： 充電樁； 工作誤差； 灰色預測； 在線計量； 模型融合； 灰狼算法

中圖分類號： TN06?34" " " " " " " " " " " " " " "文獻標識碼： A" " " " " " " " " " " " 文章編號： 1004?373X（2024）05?0112?06

Research on DC charging pile online measurement error prediction method

based on improved GWO?GM（1，1） model

CHEN Ping1， ZHOU Juan1， WU Minggong2

（1. College of Quality and Safety Engineering， China Jiliang University， Hangzhou 310018， China; 2. Anhui Institute of Metrology， Hefei 230051， China）

Abstract： Since the prediction accuracy of the traditional grey theory is not high and the basic grey wolf optimization （GWO） algorithm is prone to falling into the local optimum， a DC charging pile online measurement error prediction model based on improved GWO algorithm and grey theory is proposed. Vector synthesis is carried out by differential mutation strategy， and nonlinear mutation probability [k] is introduced to enhance the global search ability in the early stage， balance the global and local search ability of GWO algorithm， and avoid falling into the local optimal. Then， the improved algorithm is applied to the GM（1，1） model， and a group of grey wolf positions with the best fitness value are found by several iterations， and the optimal background value is found to optimize the grey model and further improve the prediction accuracy of the model. In comparison with the verification model before and after improvement， the mean square error and mean absolute error of the improved grey prediction model are reduced by 70.7% and 27.2%， respectively， which verifies the effectiveness of the proposed method.

Keywords： charging pile; working error; grey prediction; online measurement; model merging; GWO algorithm

0" 引" 言

新能源汽車產業不斷發展，歐美等國家紛紛提出禁售燃油車計劃[1]。截至2022年，我國新能源汽車銷量連續7年全球第一[2]。未來新能源汽車的大規模發展將進一步促進充電設施的大面積安裝與配置[3]。充電樁作為支撐新能源汽車產業發展的基礎設施，截至2021年底，全國充電設施規模[4]達到261.7萬臺。存量多、增幅快對充電樁計量的精度和速度提出較高要求[5]。傳統充電樁檢定方法是利用充電樁檢定裝置或集成的車載系統進行現場檢定，選擇恒壓或者恒流充電方式在三個負載點充電兩次，取平均誤差[6]。這樣得出的誤差點較少，且對其他點的工作誤差也無法判斷。為了能對大量的充電設施進行有效、快捷的計量監管，物聯網技術開始逐漸應用于現場檢測和監管中[7?9]。國內許多檢測機構把遠程在線計量作為研究方向，這種方式可以理解為在線計量監管[10]。目前對于充電樁計量方法的研究有：通過設計云平臺實現虛擬化的智能監測[11]，基于模型算法對充電樁計量性能進行評估研究[12?13]。上述方法主要針對充電樁的數據進行在線監測評估，現場充電環境下不穩定因素較多，對于充電設施的計量誤差預測研究較少。

傳統灰色預測模型不需要大量數據，適合中短期預測，適用領域較廣[14]，在誤差預測方面有較好的應用，但鮮見將灰色理論應用于充電樁工作誤差預測方面。隨著對灰色理論精度要求的提高，文獻[15]提出改變構造背景值的權重系數提高模型預測精度，并通過實例數據進行了驗證。文獻[16]提出通過對原始序列進行多項式擬合，應用于水庫的徑流預測，精度提高明顯。文獻[17]提出利用最小一乘法對參數進行尋優，應用于衛星鐘差預報，從而提高預報的準確性。上述改進僅限于單一模型內，隨著應用領域范圍變廣，基于多算法融合改進的建模趨于增多。文獻[18]提出BP神經網絡結合灰色預測模型針對水上交通事故的預測，相較單一模型精度提高。文獻[19]提出改進的蜂群算法和灰色預測相融合的模型，利用蜂群算法全局搜索能力強的特點優化灰色模型的背景值，并應用于管道腐蝕預測研究。文獻[20]提出一種灰色BP神經網絡，將灰色預測數據作為BP神經網絡的輸入，實現模型的優勢互補，提高預測精度。這些方法相較于傳統灰色模型改進方式明顯，模型整體精度提高，然而在充電樁實際充電過程中，充電初期往往電能量較小，工作誤差較大，充電后期工作誤差逐漸變小趨于平穩。因此，對個別電能量點的工作誤差預測提出較高要求。針對上述情況，本文提出改進的灰狼算法優化模型的背景值并應用于在線計量數據預測。首先是通過差分變異策略平衡灰狼算法的全局和局部搜索能力，解決其易陷入局部最優的問題。接著提出優化灰狼算法改進灰色預測模型即GWO?GM（1，1）預測模型，將改進的灰狼算法應用于GM（1，1）模型中，通過多次迭代尋找到最優背景值對灰色模型進行優化，進一步提高模型的預測精度。最后將GWO?GM（1，1）模型應用于充電樁在線計量工作誤差的預測中，解決了充電樁初期誤差波動較大、預測精度不夠的問題。

1" 傳統模型分析

1.1" 傳統灰色預測模型方法

原始離散數據序列[x0=x0（1），x0（2），…，x0（n）]，其中[n]為序列長度，上標中的0表示累加次數0次。按式（1）對其進行一次累加生成處理，得到序列[x1=x1（1），x1（2），…，x1（n）]，其中，[x0（1）=x1（1）]。以序列[x1=x1（1），x1（2），…，x1（n）]為基礎建立灰色的生成模型[21]：

[x1k=j=1kx0j，" "k=1，2，…，n] （1）

式（2）稱為一階灰色微分方程，記為GM（1，1）。

[dx1dt+ax1=u] （2）

式中：[a]和[u]為待辨識參數。

設參數向量：

[a=auT] （3）

[yn=x02，x03，…，x0nT] （4）

[z1k=μx1k-1+1-μx1k] （5）

[B=-x12+x1121??-x1k+x1k-121] （6）

則由式（7）求得[a]的最小二乘解：

[a=BTB-1BTyn] （7）

得到響應方程為：

[x1k+1=x11-uae-ak+ua] （8）

但模型得出的是一階累加量，建模運算后需作逆生成。

[x0k+1=x1k+1-x1k] （9）

1.2" 預測模型的后驗差檢驗

利用關聯度及后驗差對預測模型進行檢驗，記0階殘差為：

[ε0i=x0i-x0i，" " i=1，2，…，n] （10）

式中[x0（i）]為通過預測模型得到的預測值。

殘差均值：

[ε0=1ni=1nε0i] （11）

殘差方差：

[S21=1ni=1nε0i-ε02] （12）

原始數據均值：

[x=1ni=1nx0i] （13）

原始數據方差：

[S22=1ni=1nx0i-x2] （14）

可計算后驗差檢驗指標，后驗差比值[c]如下：

[c=S1 S2] （15）

小誤差概率[P]為：

[P=Pε0i-ε0lt;0.674 5S2] （16）

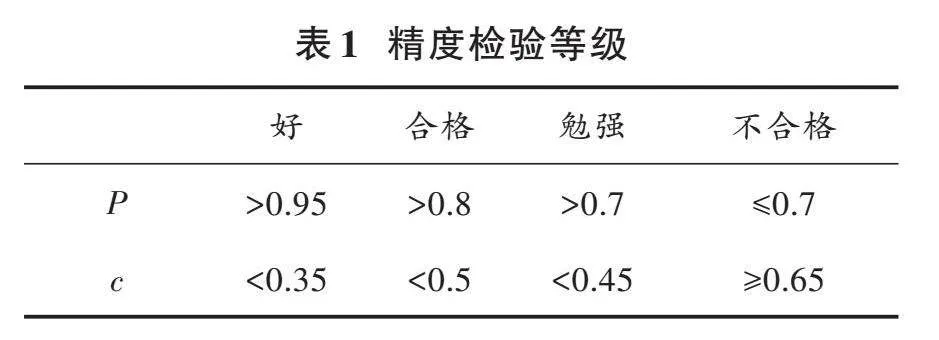
精度檢驗等級如表1所示。

2" 改進型GWO?GM（1，1）預測模型

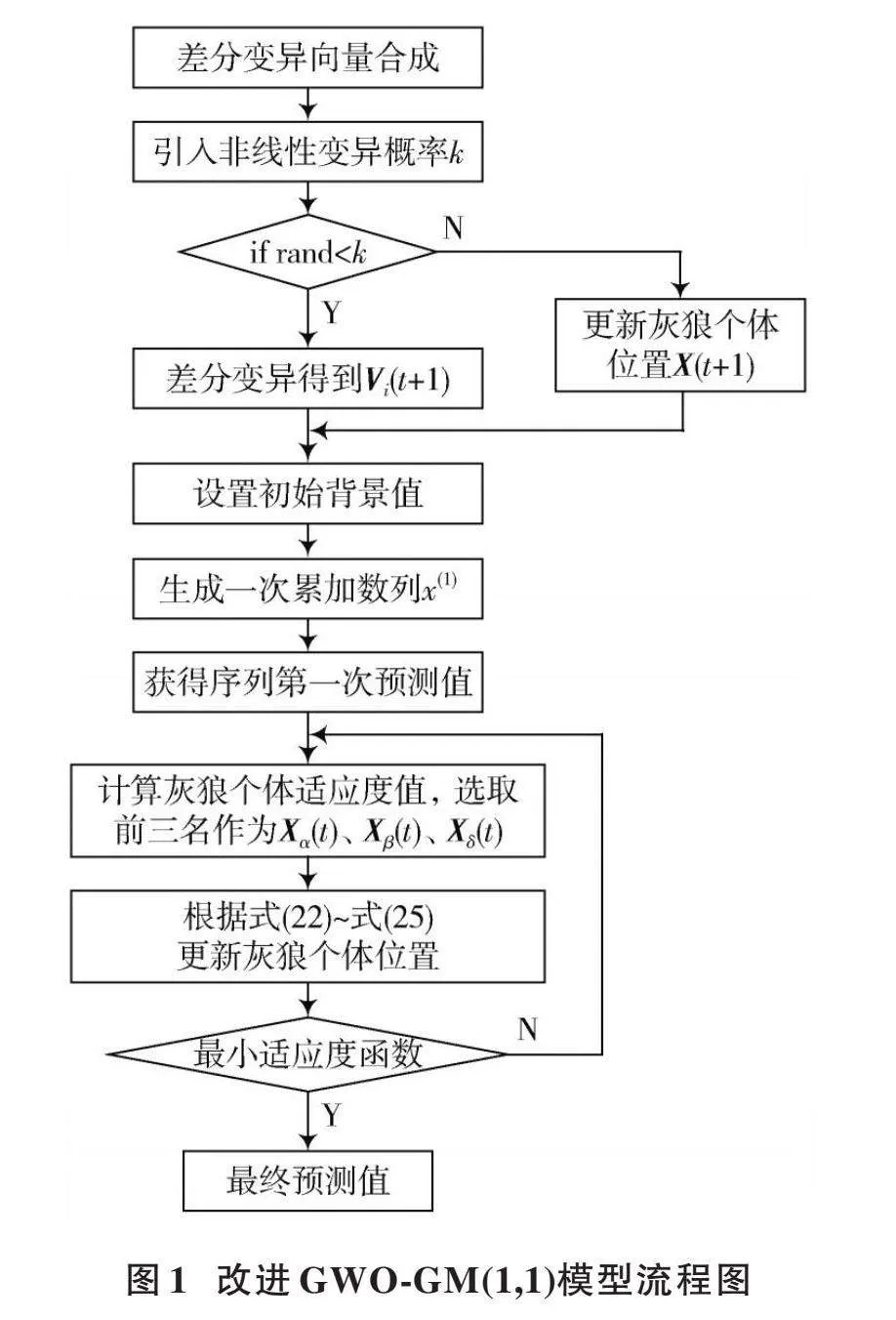
傳統的灰色預測模型中一般將背景值設置為0.5，雖然簡化了計算過程，但由此也產生了誤差，降低了預測精度。背景值帶來的偏差也會大大提高建模時的系統誤差。因此，背景值的選取對于預測模型精度至關重要[22]。本文結合灰狼算法尋找最優解，通過差分變異優化模型對GM（1，1）模型背景值進行優化，建立綜合模型以進一步提高系統預測精度。改進模型流程圖如圖1所示。

2.1" 灰狼算法分析

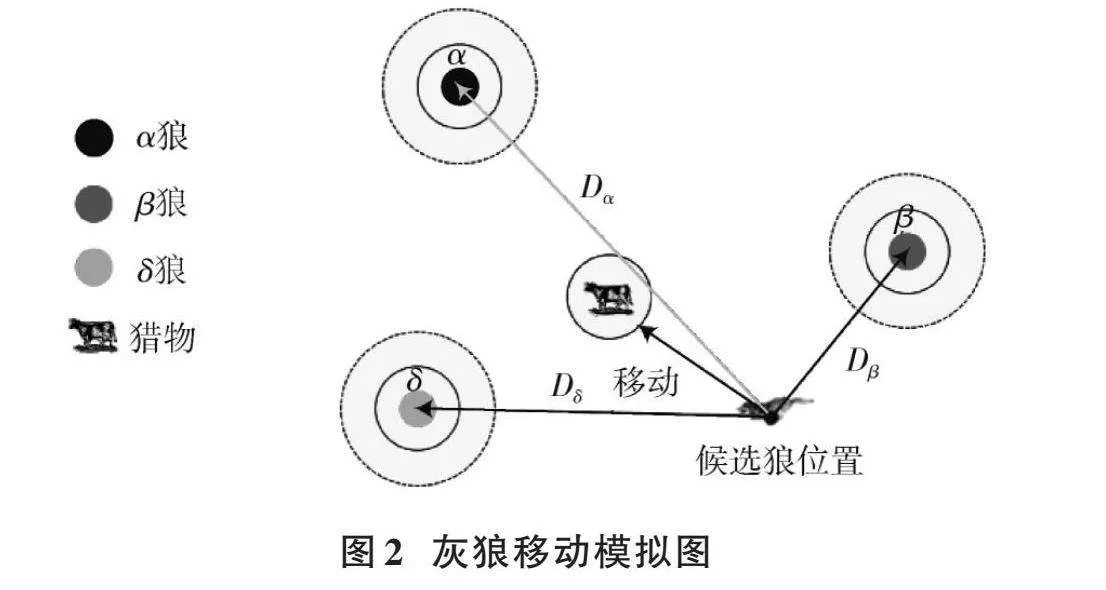
灰狼優化算法（Grey Wolf Optimization， GWO）模擬自然界灰狼種群捕食行為[23]。灰狼個體會向群體中最優的三個個體移動，該算法數學模型簡單，適應于不同領域的復雜問題。主要包括跟蹤追趕獵物、包圍逼近獵物及攻擊逮捕獵物三個階段。灰狼算法模擬圖如圖2所示。

當狼群向獵物逐漸逼近時，對距離和方位作出如下定義[24]：

[D=C?XPt-Xt] （17）

[Xt+1=XPt-A?D] （18）

式中：[XPt]代表灰狼在經過第[t]次選代后計算出的獵物當前所在位置向量；[Xt]代表灰狼個體經過[t]次送代后所處的位置向量，即算法的局部最優解位置；[A]和[C]為包圍獵物過程中所產生的隨機系數，[A=2a?r1-a]，[C=2r2]，[a]隨著迭代次數的增加從2線性遞減到0，[r1]和[r2]是在區間[0，1]中產生的隨機數。

在包圍獵物階段，由于在一個抽象的空間中并不知道最優獵物的位置。為了更科學地模擬灰狼捕捉獵物的行為，假定[α]、[β]和[δ]對獵物的潛在位置有著較強的識別能力，通過保存獲得的前三個最佳解決策略，并讓其他狼根據前三個最佳策略來更新代替現有的位置，其數學表達式如下：

[Dα=C1?Xαt-Xt] （19）

[Dβ=C2?Xβt-Xt] （20）

[Dδ=C3?Xδt-Xt] （21）

式中：[Dα]、[Dβ]和[Dδ]分別表示[α]、[β]和[δ]狼與其他灰狼個體之間的距離；[Xαt]、[Xβt]和[Xδt]分別代表第[t]次選代后[α]、[β]和[δ]狼當前位置；[Xt]代表當前灰狼個體位置。

[X1=Xαt-A1?Dα] （22）

[X2=Xβt-A2?Dβ] （23）

[X3=Xδt-A3?Dδ] （24）

[Xt+1=X1+X2+X33] （25）

式中[X1]、[X2]、[X3]分別代表的是灰狼個體朝前三個潛在解[α]狼、[β]狼和[δ]狼的步長和方向。式（25）代表灰狼個體的最終位置。

2.2" 改進型灰狼算法

灰狼算法根據灰狼群體的捕獵行動而提出，其算法流程和步驟簡單明了，在探索和開發兩個階段具有較強的平衡性，算法中個體不停移動導致全局搜索能力更強。但迭代過程中往往會陷入局部最優的情況，由式（25）可知，灰狼個體的最終位置由潛在解[α]狼、[β]狼和[δ]狼決定，如果潛在解存在局部最優，則會導致整個算法陷入局部最優，出現過早收斂的現象。

針對這一情況，提出隨機差分變異，基于變異突破局部最優，提高搜索范圍，達到平衡全局和局部的搜索能力。常見差分策略是隨機選取種群中兩個不同的個體，將其向量差縮放后與待變異個體進行向量合成[25]。

[Vit+1=Xr1t-FXr2t-Xr3t] （26）

[F=0.5+0.5rand] （27）

式中：[Xr1]、[Xr2]和[Xr3]分別為狼群中隨機挑選3只個體狼的位置向量，且個體狼[ri∈1，N]；[F]為縮放因子。

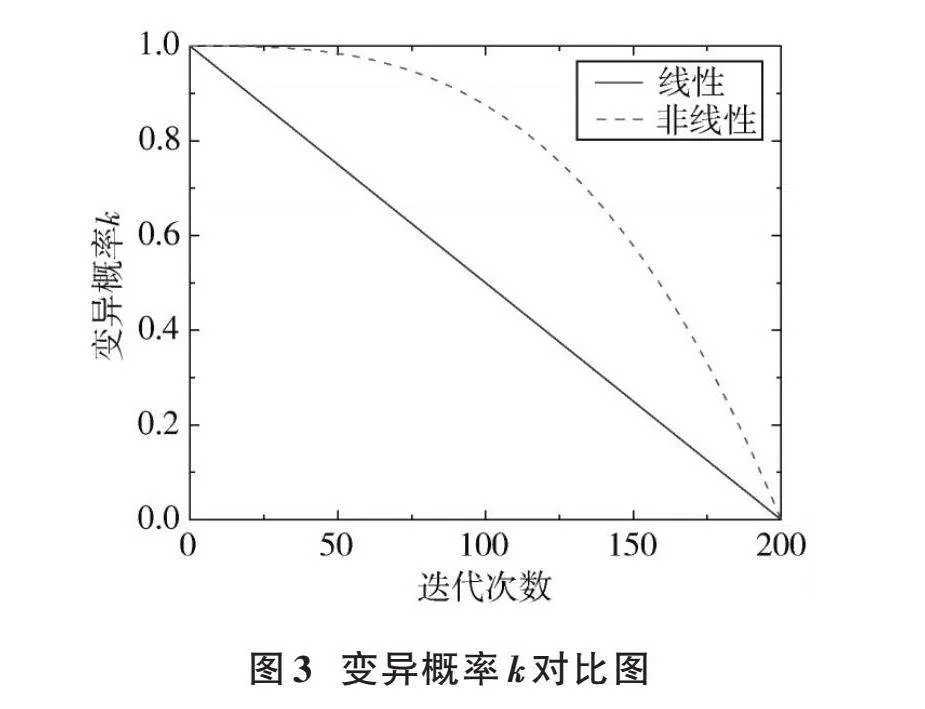
為了進一步增強算法前期全局找尋獵物的能力，故引入非線性變異概率[k]，公式如下：

[k=1-ttmax3] （28）

式中：[t]表示迭代次數；[tmax]為最大迭代次數。在迭代初始階段變異概率取值相對較大，減小幅度較小，有利于增強其全局搜索能力；隨著迭代次數的增加，后期灰狼個體的位置迭代幅度逐漸變小，[k]值的減幅越來越大，有利于增強后期局部搜索能力，非線性優勢越來越明顯。[k]值的變化對比圖如圖3所示。

因此，將隨機差分變異與灰狼算法結合，具體步驟如下：

If" "randlt;[k]，

[Vit+1=Xr1t-FXr2t-Xr3t]，

Else" " [Xt+1=XPt-A?D]。

2.3" 改進型GWO優化GM（1，1）預測模型

通過尋找灰狼算法中適應度值最好的一組灰狼位置，進而選取到最優背景值來改進模型。因此，希望模型中的目標函數即誤差越小越好，故適應度函數選取實際值與模型預測值的最小相對誤差作為選擇背景值的依據[26]，從而得到優化過的背景值并用于建立灰色預測模型，降低模型計算誤差。具體步驟如下：

Step1：設置初始背景值、最大迭代次數和種群規模；

Step2：根據原始數據生成一次累加數列[x1]，建立灰色模型，并由公式（9）獲得初始預測值；

Step3：計算灰狼個體適應度值，選取前三名作為[Xαt]、[Xβt]、[Xδt]；

Step4：根據式（22）～式（25）更新灰狼個體位置；

Step5：計算適應度函數是否最小，若最小，則輸出最終預測值，否則，重復Step3和Step4。

3" 模型的應用與檢驗

3.1" 原始數據分析與處理

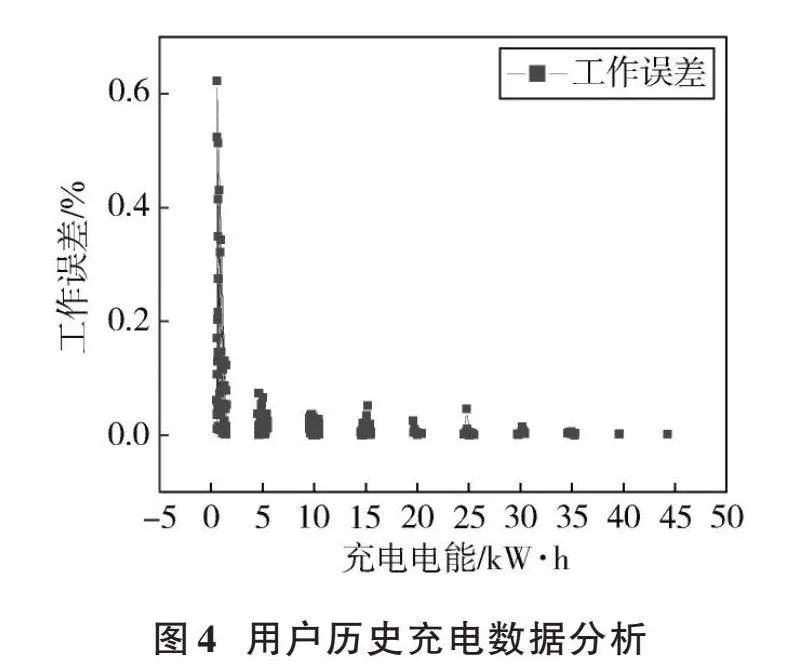
將改進后的模型應用到在線計量監測裝置上，調取編號為3401040152401的直流充電樁從2021年11月—2022年8月的充電電能和工作誤差數據記錄。將后臺選取的近1 000組工作誤差數據按充電電能大小進行分析。數據呈典型的非線性相關關系，且充電初期誤差較大，總體數據如圖4所示。

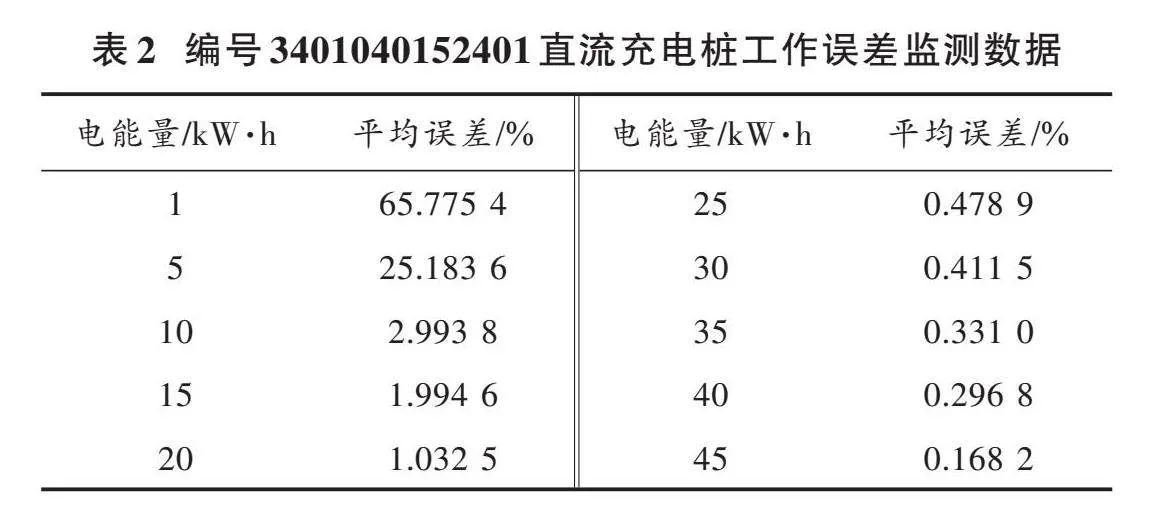
從大數據中只能看到一種趨勢，在低電能量附近整體工作誤差偏高，隨著電能量增加誤差迅速降低。因此，選擇有代表性的點進行詳細分析，通過選擇（1±0.5）kW·h～（45±0.5）kW·h等10個點的工作誤差作為原始數據，利用前8個數據點對后2個電能值點進行預測，個別電能值點由于數據較少，把充電范圍擴大為±1 kW·h，根據JJG1149檢定規程，先將這些工作誤差點取絕對值，再求平均值。采用四舍五入的方式保留4位有效數字，得到第一組初始序列[x0]，接著將計算出的10個點的數據繪制成表2。通過對改進前后模型的誤差數據對比，并與實際情況作比較，做出分析和判斷。

3.2" 獲取最優適應度值與改進前后對比

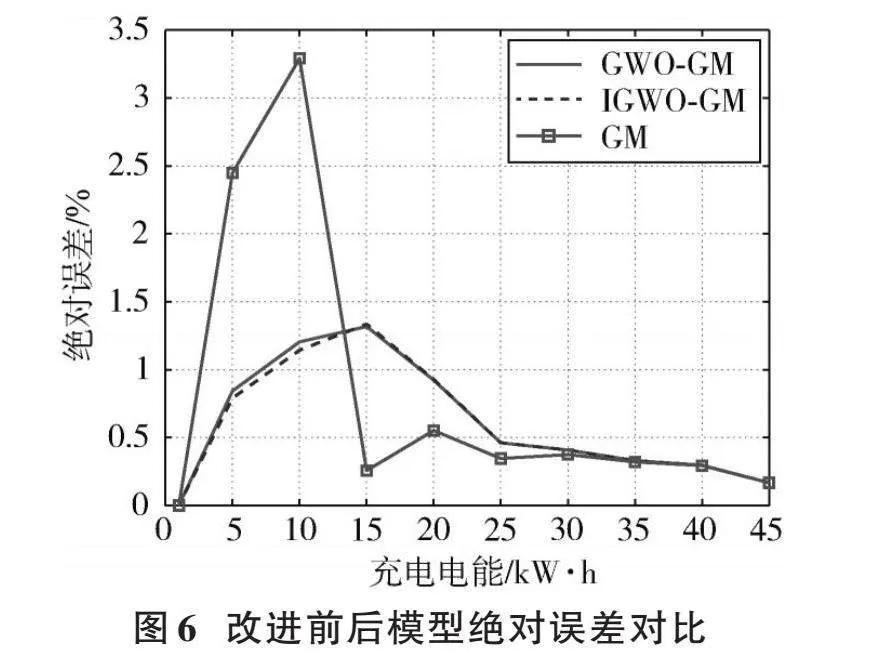
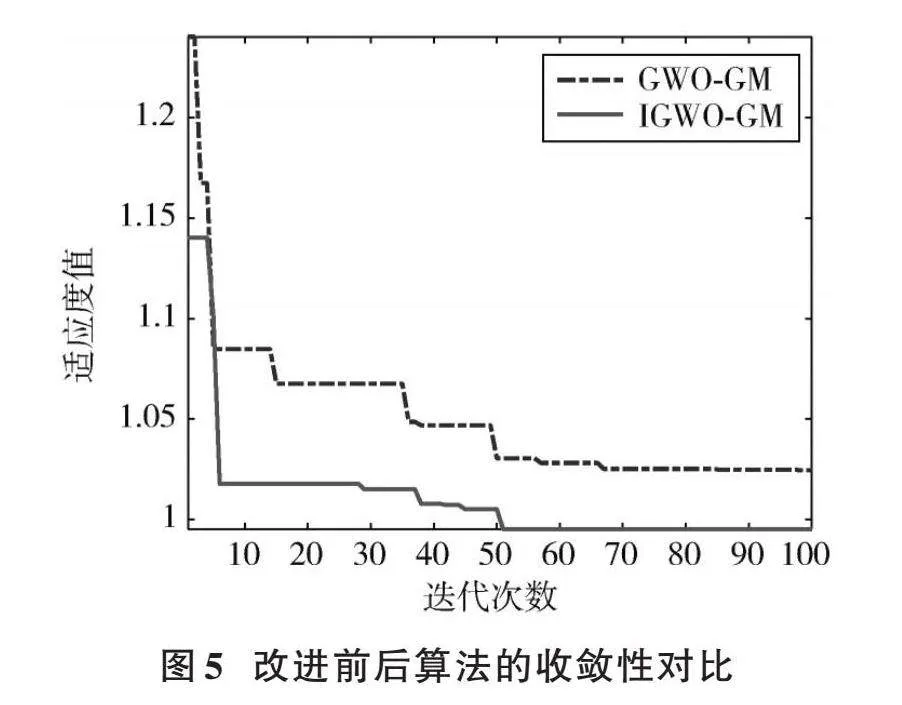
經過計算灰狼個體適應度值，選取適應度值最優的前三名分別為[Xαt]、[Xβt]、[Xδt]，根據式（22）～式（25）更新灰狼個體位置，計算適應度函數是否最小作為判斷依據，并得出最終預測值。改進前后算法的適應度值收斂性對比如圖5所示，絕對誤差對比如圖6所示。

從圖5和圖6中可以發現：

1） 改進后的模型通過迭代整體適應度值更低，大約在51代后尋找到最優適應度值。

2） 隨著電能量的增加，工作誤差整體波動幅度變小，這也從側面反映出隨著充電電能的增加，計量準確性在提高。

3） 在電能量5 kW·h之前不管是預測的工作誤差還是初始值的工作誤差，整體誤差偏高，與實際的現場檢測情況也是吻合的。

原因分析如下：

1） 現場檢定中往往會使用恒流或恒壓的模式進行各個負載點的誤差檢定，充電初始充電樁和負載整個系統還未達到穩定運行狀態，且充電樁在實際充電過程中會根據充電電流及電壓的大小進行并聯使用，這就要求充電樁擁有能夠均流輸出的功能，因此在達到穩定輸出之前誤差相對較高。

2） 直流充電樁正常工作，輔助電源需要給控制、顯示、信號采集等單元和刷卡模塊等控制系統進行供電，此外，輔助電源還需要給BMS進行供電，由BMS系統實時監控動力電池的狀態，這些系統正常工作都需要一個穩定過程。

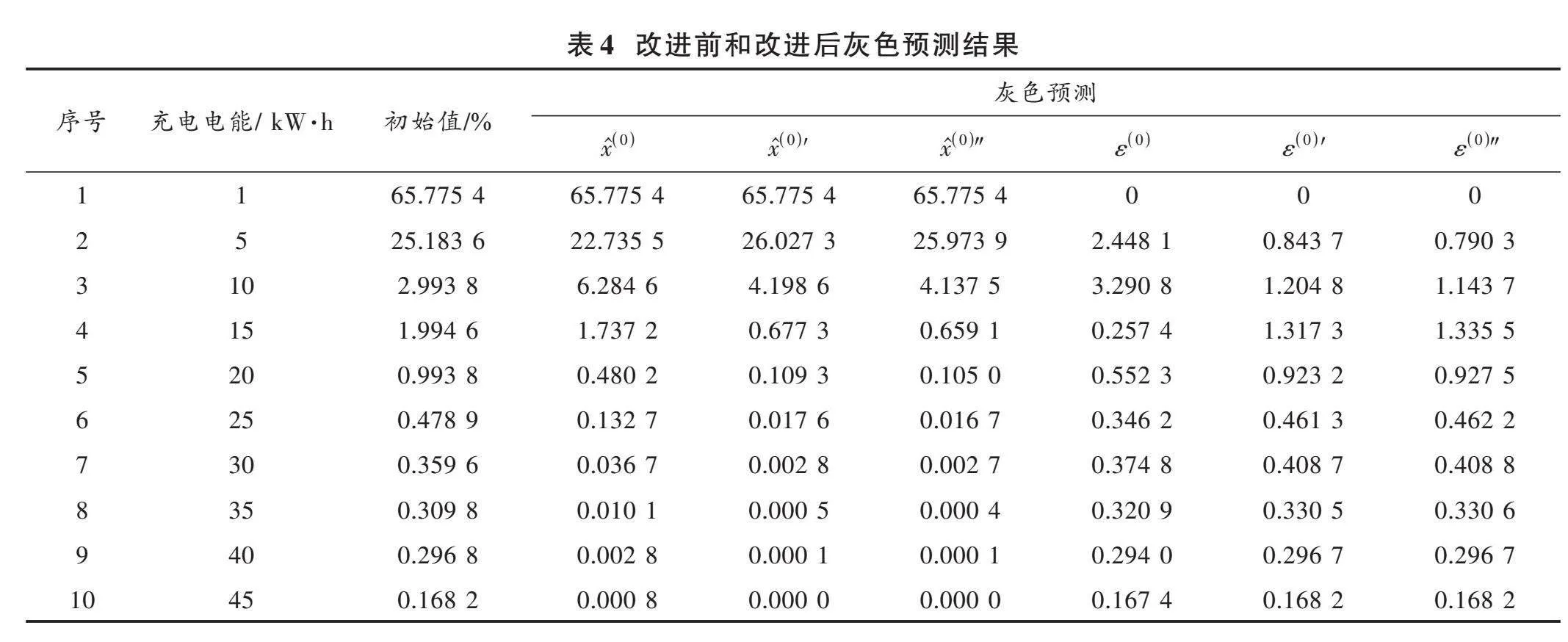
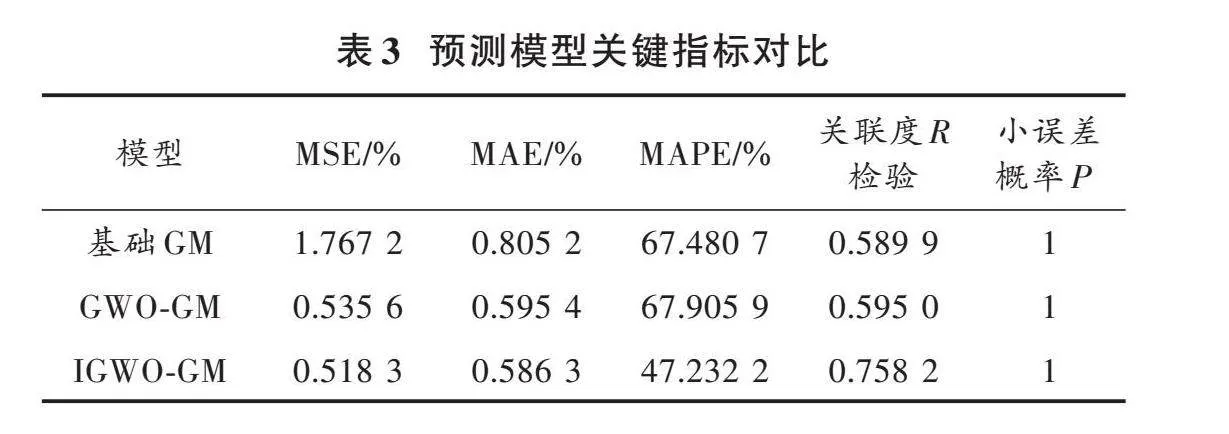
通過初始值預測出改進前的工作誤差[x0]和改進后的工作誤差[x0′]以及三個不同模型的0階殘差[ε0]、[ε0′]和[ε0″]，預測模型的關鍵指標和計算結果見表3和表4。由表中數據發現，改進的灰色預測模型相較于基礎的灰色模型均方誤差與平均絕對誤差分別降低了70.7%和27.2%，關聯度[R]也有了較大提升。

3.3" 非線性回歸模型檢驗與分析

通過改進的灰色理論模型可以看出，隨著充電電能量的增加，工作誤差整體處于越來越低的水平，而且趨向相對平穩的狀態。對灰色預測的數據進行非線性回歸分析，將灰色預測函數定義為：

[y=a+bx] （29）

式中：[x]為自變量充電電能；[y]為因變量工作誤差；經過多次迭代找出[a]估算值是-1.130；[b]的估算值是68.956。模型擬合度[R2]達到了0.951。

通過上述分析，既驗證了灰色預測模型的正確性，同時表明模型的預測結論是正確的。

4" 結" 論

本文通過改進GWO?GM（1，1）模型進行直流充電樁在線計量誤差預測，得出以下結論：

1） 通過改進的灰狼算法來優化灰色預測模型中的背景值，進一步提高了灰色預測模型精度，結合實際數據發現優化后的模型均方誤差和平均絕對誤差大幅降低，關聯度顯著提高。

2） 通過灰色理論模型的預測發現，在線計量的工作誤差與初始預測的值基本一致，通過后驗差和非線性回歸兩種方式進行檢驗，非線性回歸模型中擬合度[R2]達到0.951，驗證了方法的有效性。

3） 引入變異概率[k]，平衡了其全局和局部搜索能力，再應用于優化灰色預測，通過兩種模型的有效融合，改進了充電初期誤差波動較大、預測精度低的問題。

注：本文通訊作者為周娟。

參考文獻

[1] YU Z， CHOU S Y. Research on ratio of new energy vehicles to charging piles in China [J]. Computer systems science and engineering， 2022， 42（3）： 963?984.

[2] 洪吉超，梁峰偉，楊京松，等.新能源汽車產業及其技術發展現狀與展望[J].科技導報，2023，41（5）：49?59.

[3] ZHANG T， ZHENG L， JIANG Y， et al. A method of chained recommendation for charging piles in Internet of Vehicles [J]. Computing， 2021， 103： 231?249.

[4] 李曉敏，劉毅然.充電基礎設施對新能源汽車推廣的影響研究[J].中國軟科學，2023（1）：63?72.

[5] 賀青，邵海明，梁成斌.電磁計量學研究進展評述[J].計量學報，2021，42（11）：1543?1552.

[6] 吳名功，吳曉燕.充電設施工作誤差在線檢定方法探討[J].工業計量，2021，31（6）：3.

[7] DONG W， ZHANG H. Design of multi?channel electric energy metering and charge?monitoring system [C]// 2017 3rd IEEE International Conference on Control Science and Systems Engineering （ICCSSE）. New York： IEEE， 2017： 391?395.

[8] CHENG N， SU Y Q， ZHENG P. A detection method of electricity stealing behavior of charging pile based on CNN?LSTM [C]// 2021 3rd Asia Energy and Electrical Engineering Symposium （AEEES）. [S.l.： s.n.]， 2021： 655?659.

[9] CHEN Z R， LI F C， XU X G， et al. Research on remote calibration system of DC metering device for electric vehicle charging piles based on embedded [C]// 2019 IEEE 3rd Information Technology， Networking， Electronic and Automation Control Conference （ITNEC）. New York： IEEE， 2019： 300?304.

[10] 岳紅權，王建淵，楊文宇，等.基于互聯網+的充電站配電設備在線監測研究[J].電網與清潔能源，2018，34（4）：29?35.

[11] 陳藍生.基于云平臺的充電樁虛擬智能計量檢測與管理裝置設計[J].計量學報，2019，40（z1）：116?121.

[12] 卜樹坡，陳麗，趙展.基于超閾值分布的直流充電樁計量準確性預測研究[J].電測與儀表，2021，58（10）：145?150.

[13] 劉煒，王朝亮，肖濤，等.AMI數據驅動的電動汽車充電設施計量運行誤差狀態評估方法[J].電力自動化設備，2022，42（10）：70?76.

[14] 閆海霞，王秋萍，郭佳麗.基于飛蛾火焰優化算法的改進GM（1，1）模型[J].西安理工大學學報，2022，38（1）：69?74.

[15] 楊國華，顏艷，楊慧中.GM（1，1）灰色預測模型的改進與應用[J].南京理工大學學報，2020，44（5）：575?582.

[16] 武桂芝，王程.基于擬合改進的徑流灰色預測模型研究[J].人民黃河，2020，42（10）：34?36.

[17] 于燁，黃默，王小青，等.利用最小一乘法改進的灰色模型的導航衛星鐘差預報[J].測繪通報，2019（4）：1?6.

[18] ZHAO Y， FAN Z Z， ZHAO C. Combined forecasting model of water traffic accidents based on gray?BP neural network [C]// 2019 4th International Conference on Intelligent Transportation Engineering （ICITE）. New York： IEEE， 2019： 34?38.

[19] 秦謝勛，劉文彬，陳良超.基于改進蜂群算法和灰色模型的管道腐蝕預測[J].北京化工大學學報（自然科學版），2021，48（1）：74?80.

[20] 孫成勝，張紅民，王艷，等.一種改進的灰色BP神經網絡光伏出力預測方法[J].重慶理工大學學報（自然科學），2020，34（2）：217?221.

[21] 熊遠南.基于改進灰色?多元回歸組合預測模型的燃煤電廠智慧水務研究[J].化工進展，2020，39（z2）：393?400.

[22] 岳希，楊洋.基于最小誤差化的GM（1，1）模型的優化及應用[J].計算機應用研究，2016，33（8）：2328?2330.

[23] 周克良，鄧飛翔，王威.基于IGWO?PID預測算法的水輪機調速控制[J].現代電子技術，2021，44（23）：121?125.

[24] 曹軻，譚沖，劉洪，等.基于改進灰狼算法優化BP神經網絡的無線傳感器網絡數據融合算法[J].中國科學院大學學報，2022，39（2）：232?239.

[25] 盧純義，于津，余忠東，等.基于改進灰狼算法優化SVR的混凝土中鋼筋直徑檢測方法[J].計算機科學，2022，49（11）：228?233.

[26] 張英芝，朱繼微，劉津彤，等.改進灰狼算法優化灰色預測模型在數控機床中的應用[J].制造技術與機床，2022（3）：127?131.