建模：在體驗中運用數學語言

【摘 要】數學體驗是包含體覺、體察、體悟、體證四個緊密相連階段的一種學習方式。在初中數學教學中，教師可以基于“體覺下的模型準備—體察中的模型假設—體悟里的模型構建—體證內的模型驗證—體驗間的模型迭代”的數學體驗教學模式，通過構建數學模型活動、應用數學模型活動、實施綜合實踐活動等策略，培養學生模型意識，發展學生模型觀念，提升學生模型思想，實現數學學科育人目標。

【關鍵詞】初中數學；數學體驗；數學語言；建模；教學模式

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2024）27-0022-06

【作者簡介】1.朱敏龍，南京市第二十九中學（南京，210029）初中部副校長，高級教師；2.石小虎，南京市金陵匯文學校（南京，210036）教師，高級教師；3.何衛群，南京市育英第二外國語學校（南京，210044）教師，高級教師；4.田禹，南京市金陵匯文學校（南京，210036）教師，一級教師。

《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）在“核心素養內涵”中提出，通過數學的語言，可以簡約、精確地描述自然現象、科學情境和日常生活中的數量關系與空間形式；能夠在現實生活與其AoU1nCOHuLvKxX8rLVnIvg==他學科中構建普適的數學模型，表達和解決問題；形成數學的表達與交流能力，發展應用意識與實踐能力。在義務教育階段，數學模型是數學語言的一種主要表現形式。學生通過經歷用數學語言表達現實世界中的數量關系與空間形式的過程，初步感悟數學與現實世界的交流方式，能夠有意識地運用數學語言表達現實世界與其他學科中事物的本質、關系和規律，并解釋表達的合理性；欣賞數學語言的簡潔與優美，逐步養成用數學語言表達與交流的習慣，形成跨學科的應用意識與實踐能力。

一、數學模型的內涵和要義

（一）數學模型的內涵

數學模型是利用數學語言、符號和邏輯，對現實世界中的特定對象、現象或過程進行抽象和簡化的描述，它是基于數學理論構建的、能夠反映實際問題本質特征和內在規律的數學結構。廣義上說，數學模型就是為解決現實生活中的問題而建立的數學概念、公式、定理、法則、規律、性質、數量關系式、圖形、圖標、程序等。例如，路程等于速度乘以時間，是描述行程問題中數量關系的數學模型；圖形的周長、面積計算公式，是描述圖形某一方面特性的數學模型。狹義地講，數學模型指那些反映了特定問題或具體事物系統的數學結構，如“雞兔同籠”“抽屜原理”“將軍飲馬”等典型的數學模型。

（二）數學模型的要義

數學模型是對實際問題的一種數學化描述和表達，它的要義主要有以下幾方面。

1.抽象與簡化

數學模型是對現實世界的抽象和簡化。現實世界中的事物往往非常復雜，難以直接進行研究和處理。利用數學模型，我們可以將復雜的現實問題轉化為數學語言，從而簡化問題，使其更易于分析和解決。數學模型忽略了一些次要因素，保留了問題的主要特征和規律。抽象、簡化的模型能夠使得現實問題更加易于處理和分析，同時也有助于揭示問題的本質。

2.結構與系統

數學模型是一種數學結構或系統，這種結構或系統通常由一系列的數學符號、代數式、方程、不等式、函數等組成，它們共同描述了現實世界的某個方面或某個過程。這些數學表達形式能夠精確地描述問題的結構、關系和變化規律，讓學生可以通過數學方法求解現實問題。這些數學元素相互關聯、相互作用，形成了一個完整的體系。

3.預測與決策

利用數學模型，我們可以對現實世界的現象進行定性和定量的分析，揭示其內在規律和機制。大數據時代，數據觀念、數據分析變得越來越重要，逐漸形成了一種新的數學語言。通過分析和計算由數學語言建構的模型，可以預測未來的發展趨勢或結果，從而為決策提供科學依據。

4.通用性與推廣性

數學模型往往具有一定的通BUi4GArKfOqbP5+xBnO61A==用性和推廣性，即同一類問題可以使用相同的模型進行描述和解決。這使得數學模型在各個領域都有廣泛的應用，如物理學、經濟學、生物學等。

二、數學建模對運用數學語言的意義

數學建模（以下簡稱“建模”）指利用數學方法和工具，對實際問題進行抽象、簡化和量化，建立數學模型，并通過求解模型來解決問題的一種科學方法。建模的意義在于鼓勵學生將他們的解決方案和思考過程，通過口頭陳述、寫作、圖表、圖像等形式進行有效的交流和表達。在表達過程中，學生需要運用恰當的數學語言來解釋他們的解決方案、推理過程和結論；需要使用準確的數學術語和符號清晰地描述他們的思考路徑，并提供合理的解釋和證明，從而能創新性地運用到相關生活問題的解決中。

因此，通過建模，學生可以深入了解問題的本質和規律，發現其中的數學結構和關系。同時，建模也是培養學生創新精神和實踐能力的重要途徑。

三、以建模為體驗意義的數學體驗教學模式的框架

數學體驗為建模提供了重要的方法基礎，學生在數學體驗學習中，建立數學模型，運用數學模型解決現實問題，親身感受數學的應用價值，能夠激發對建模的興趣和動力。同時，將建模成果應用于實際問題的解決過程中，通過實踐檢驗模型的準確性和有效性，可以進一步豐富學生的數學體驗。數學體驗作為一種學習方式，包含體覺、體察、體悟、體證四個緊密相連的階段，具有身心合一、內外并舉、知情并重、過程與結果相統一等特征。它順應新時代課程改革的要求，可使學生的數學認知能力得到提升，有利于學生正向的情感態度與價值觀的形成，有助于實現由數學知識向數學素養的轉化。以建模為體驗意義的數學體驗教學模式的基本框架如下：

（一）體覺下的模型準備（項目與問題呈現）

體覺即啟動經驗，初步感覺。體覺下的模型準備就是圍繞將要學習的內容，明確建模目標，啟動、激發與新知識相關聯的原有知識經驗，并收集相關數據，從而深入理解問題背景與系統特性，進而形成初步的感覺和深入探究的欲望，為模型雛形建構作準備。在這一環節，教師可以根據學習目標，創設貼近學生的生活情境，設計體驗教學模式基本框架中的“困惑與沖突”問題，激發學生的探究熱情。

（二）體察中的模型假設（形成對項目與問題的理解）

體察即全面觀察，深入反思。體察中的模型假設就是基于現有知識和實際情況，發現和提出有價值的問題，并用恰當的數學術語和符號來描述問題的特征和要求，對系統行為做出合理簡化和理想化假設，從而實現體驗教學模式基本框架中的“直覺與聯想”。

（三）體悟里的模型構建（形成初步方案）

體悟即抽象概括，意義建構。體悟里的模型構建就是選擇適當的數學工具，如方程、不等式、函數、統計模型、優化算法、圖論模型等，將假設轉化為數學表達。

（四）體證內的模型驗證（探索加工重構）

體證即身臨其境，驗證應用。體證內的模型驗證就是運用數值方法、解析方法或模擬技術求解模型，將模型應用于實際問題。在這一環節，學生通過對比實測數據、進行定性分析或檢驗等方式驗證模型的有效性。

（五）體驗間的模型迭代（完成項目研究）

體驗即積累經驗，優化經驗。體驗間的模型迭代就是根據反饋調整模型參數或結構，進一步迭代、改進模型。

四、以“建模”為體驗意義的數學體驗教學的實施策略

以“建模”為體驗意義的數學教學可通過構建數學模型、應用數學模型和實施綜合實踐活動等策略來培養學生模型意識、發展學生模型觀念、提升學生模型思想，進而發展學生的數學建模能力和創新意識等核心素養。

（一）構建數學模型，培養模型意識

數學知識本身就是一種數學模型，學生對數學知識的學習本質上就是一種構建數學模型的學習活動，構建數學模型是學生習得數學知識的基本途徑之一。這種構建數學模型的活動，實際上是建模的某個階段或某個環節，可以培養學生的模型意識。模型意識主要指對數學模型普適性的初步感悟，知道數學模型可以用來解決一類問題，是數學應用的基本途徑；能夠認識到現實生活中大量的問題都與數學有關，并能有意識地用數學的概念與方法進行解釋。模型意識有助于增強學生對數學的應用意識，是形成模型觀念的經驗基礎。

案例1：函數模型的構建

1.體覺下的模型準備

問題：某商店專銷某種品牌的計算器，進價12元/只，售價20元/只。為了促銷，該商店決定凡是買10只以上的，每多買1只，售價就降低0.1元，但是最低價為16元/只。如果你是商家，你會有哪些思考？

2.體察中的模型假設

思考1：設賣出x只計算器，如果賣10只及10只以內，按20元/只賣；如果賣10只以上，每多賣1只，售價就降低0.1元，也就是說多賣（x - 10）只，售價就降低0.1（x - 10）元/只。

思考2：最低價為16元/只，也就是說，降價后的售價不少于16元/只，即20 - 0.1（x - 10） ≥ 16，解得x ≤ 50，賣出的計算器數不能超過50只。

思考3：作為商家，何時賺錢最多？

3.體悟里的模型構建

如何解決“何時賺錢最多”的問題呢？函數是刻畫現實世界變化規律的有效數學模型，可以建立利潤y和銷售只數x之間的函數，用函數圖象或性質分析y的取值。

設總利潤為y元，由“總利潤 = 單件利潤×件數”得：當0 ≤ x ≤ 10時，y = （20 - 12）x = 8x；當10 ＜ x ≤ 50時，y = ［20 - 0.1（x - 10） - 12］x = -0.1x2 + 9x；當x ＞ 50時y = （16 - 12）x = 4x。然后畫出分段函數示意圖，由函數圖象分析何時賺得錢最多。

將實際問題抽象化、數學化是構建數學模型活動的核心步驟。在上述體驗活動“作為商家如何智慧定價”中，學生從現實生活或具體情境中抽象出數學問題，用數學變量語言建立函數模型，表示數學問題中的數量關系和變化規律。建模活動需要教師設置生活情境，讓學生在情境中思考如何建立數學模型解決問題，這樣的數學體驗課堂設計有助于培養學生的模型意識。

（二）應用數學模型，發展模型觀念

數學建模活動是數學體驗中的一種完整的數學學習方式，關注的是建立模型和應用模型解決問題的過程。其中，應用數學模型解決問題的活動過程，主要是指建構數學模型解決應用問題，重點是培養學生階段性的數學建模能力，使其在體驗中逐漸發展模型觀念。模型觀念主要指對運用數學模型解決問題有清晰的認識，知道數學建模是數學與現實聯系的基本路徑；初步感知數學建模的基本過程，能夠從現實生活或具體情境中抽象出數學問題，并用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義。應用數學模型活動是在學生具有一定模型意識的基礎上發展其模型觀念。

案例2：如何挑選西瓜

1.體覺下的模型準備

問題：夏天，我們到超市買西瓜，在大西瓜和小西瓜中選擇，哪一種最劃算？

2.體察中的模型假設

思考：“購買西瓜”消費問題面臨兩個選擇方案（可大可小），“劃算”是指西瓜果肉部分（瓜瓤）的單價小。這里會涉及西瓜大小即質量的大小，在大小西瓜密度相同的前提下就是體積的大小，當然還有非果肉部分（瓜皮）的厚度等量。

3.體悟里的模型構建

（1）問題中包含的基本關系有：總價=單價×質量、質量=密度×體積、球體積公式V = [43]πR3等。

（2）具體數量代數化：假設當日西瓜價格為a元/千克，大、小西瓜的密度ρ相同，大西瓜的半徑為R大，小西瓜的半徑為R小，大小西瓜的厚度一樣，則可以分別用代數式表示大小西瓜果肉部分（瓜瓤）的單價a大'、a小'：a大'= [a·ρ·V大ρ·V大瓤 ]= [a·V大V大瓤]、a小'= [a·ρ·V小ρ·V小瓤] = [a·V小V小瓤]。

（3）比較這兩者的大小能夠確定挑選哪種西瓜劃算。

4.體證內的模型驗證

（1）比較兩個分式大小：a大'=[a·ρ·V大ρ·V大瓤 ]= [a·V大V大瓤 ]= [a·43π·R大343π（R大-d）3 ]=[a·R大3（R大-d）3 ]；同理，a小'= [a·R小3（R小-d）3 ]。

（2）根據分式結構特征選擇比較的方法：作商法或作差法。

5.體驗間的模型迭代

利用作商法比較分式[R大3（R大-d）3]和[R小3（R小-d）3]大小時，可以發現比較果肉的單價就是在比較果肉體積占整個西瓜體積的比例，即果肉體積占整個西瓜體積的比例大，果肉單價就低，就劃算，因此在一定條件（當日西瓜單價相同、瓜皮厚度相同、西瓜密度相同）下，購買大西瓜劃算。

現實生活中也有類似情況。生活中很多帶皮或者有殼商品的劃算問題都適用這個模型，譬如在目前受國際形勢的影響，每兩個星期國內油價也在進行相應的調整，那么等額加油與等量加油，哪種方式更劃算呢？在超市中購買某種散裝的商品時，是等額還是等量劃算呢？這些問題都可以建立數學模型，用數學的語言解釋其中的某種關系，從而解決實際問題。

建模的體驗意義重在模型建構、模型應用和模型遷移，在數學回歸于外部世界的過程中，學生體驗模型的普適性和發展性，體會數學應用的廣泛性，用數學的語言表達世界，模型觀念得到發展。

（三）實施綜合實踐活動，提升模型思想

綜合實踐活動指以現實世界中實際問題為研究對象，綜合應用學科知識（不局限于數學知識）解決實際問題的實踐活動。它是數學建模活動的重要形式，是學生參與完整的數學建模活動，是提升學生模型思想的重要途徑。模型思想即在數學中建立模型的思想。思想是人頭腦中智慧的凝聚，有助于我們形成對一個事件的認識與想法，展現人類的智慧。初中階段的綜合實踐活動，一般采用項目化學習的方式，以問題解決為導向，整合數學與其他學科的知識和思想方法，讓學生從數學的角度觀察與分析、思考與表達、解決與闡述社會生活中的現實問題。

案例3：“門格海綿”模型的構建

1.體覺下的模型準備

播放一些圖片或動畫：連綿起伏的山川、飄浮多變的云朵、深山巖石的斷裂面、錯綜復雜的大腦皮層……

這些部分與整體以某種方式相似的形體，可以說就是數學中“分形”的要義，恰恰是這些“不規則的”“分散的”“支離破碎的”物體重新讓我們認識了自然社會。它的特點簡單點講就是：每一個大的結構都可以分成幾個更小的相同的結構（可以一直分下去），這也是分形的基本原理。

教師出示“門格海綿”模型，讓學生觀察它是如何構建的（如圖1）。

2.體察中的模型假設

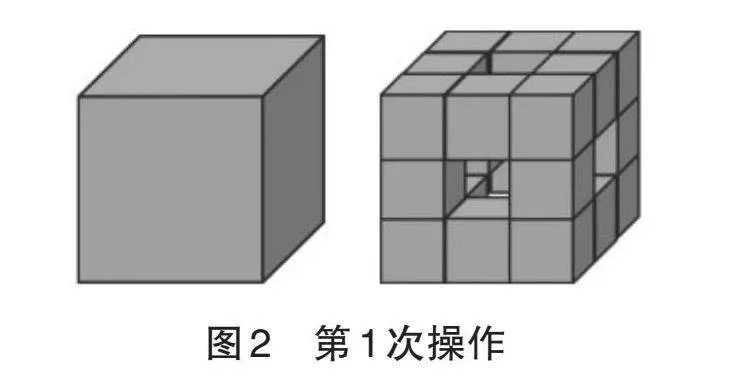
動手體驗：用土豆（紅薯或蘿卜也可）做一個正方體模型，再將每一個面平均分成9個正方形，這樣大正方體就被分成27個小正方體，把6個面的中間的正方體去掉，把最中心的正方體也去掉，留下20個正方體，以上操作我們稱為第1次操作（如圖2）。

<F：＼整理發繆老師＼中學7期＼中學7期定稿＼Image＼image2_1.png>

圖2 第1次操作

3.體悟里的模型構建

嘗試“第2次操作”，即把每一個留下的小正方體都重復上面的操作，多次操作后就能得到“門格海綿”模型，但實際操作難以做到。因此，教師可以帶領學生回憶謝爾賓斯基“地毯”的操作方法（調用各種知識形成初步方案），這種降維操作可以遷移到三維操作（如圖3）。

4.體證內的模型驗證

通過軟件迭代操作，VR裸眼3D穿越式探視等方式，學生感受、體驗和抽象出多次操作后的結果。

5.體驗間的模型迭代

親身體驗“第2次操作”，理解多次操作的可行性，完成“門格海綿”模型的項目研究。

門格海綿是一個具有數學藝術的著名模型。其每一個面都是謝爾賓斯基“地毯”（謝爾賓斯基“地毯”和它本身的一部分完全相似，減掉一塊會破壞自相似性）。自相似原則和迭代生成原則是分形理論的重要原則。它表征分形在通常的幾何變換下具有不變性，即標度無關性。標準的自相似分形是數學上的抽象，迭代生成無限精細的結構，如科契雪花曲線、謝爾賓斯基地毯曲線等。分形理論是當今世界十分風靡和活躍的新理論、新學科。

綜合實踐活動內容源于雜亂無序的現實世界，學生需要從“原生態”的現實情境中抽象出數學問題。從數學建模的過程看，上述案例通過“給出情境—發現問題—提出問題—建立模型”，讓學生經歷了完整的數學建模過程。學生參與完整的數學建模活動，是提升模型思想的重要途徑。

總之，數學建模就是讓學生親身體驗從生活現象到數學模型的提出、建立、分析、驗證、應用的過程。體驗教學在初中數學建模教學中起著至關重要的作用，從初步培養模型意識，到逐漸發展模型觀念，進而提升模型思想。因此，以建模為體驗意義的數學體驗教學模式能夠提升學生的建模能力，發展學生的核心素養，同時深入挖掘數學的科學價值與育人價值，促進數學學科育人方式的轉變。

【參考文獻】

［1］譚頂良.略論數學體驗的一些“要素” ［J］.教育研究與評論（中學教育教學），2021（7）：7-11.

［2］中華人民共和國教育部.義務教育數學課程標準（2022年版）［S］.北京：北京師范大學出版社，2022：4.

［3］王永春.小學數學與數學思想方法［M］.上海：華東師范大學出版社，2014：30.