基于多策略改進的SMC?GTO電機速度跟蹤控制

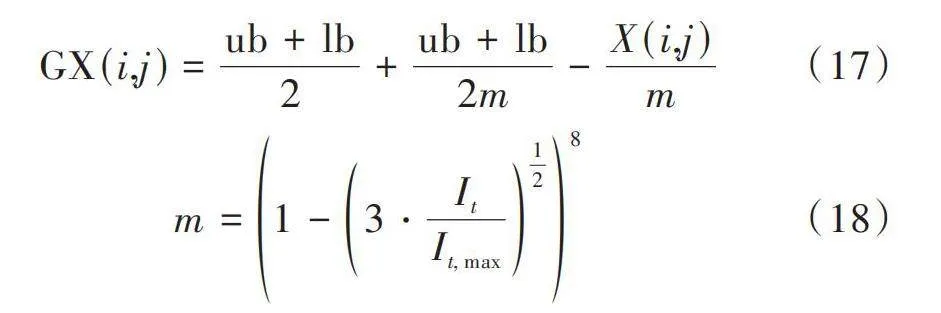
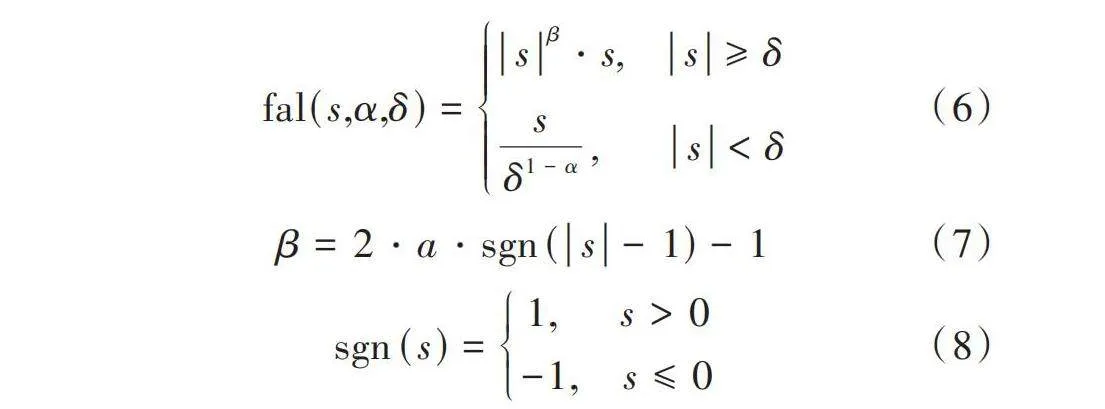
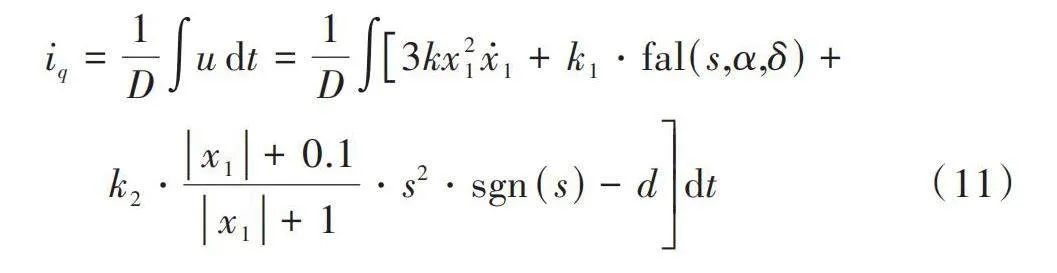
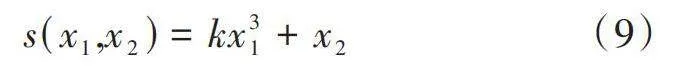
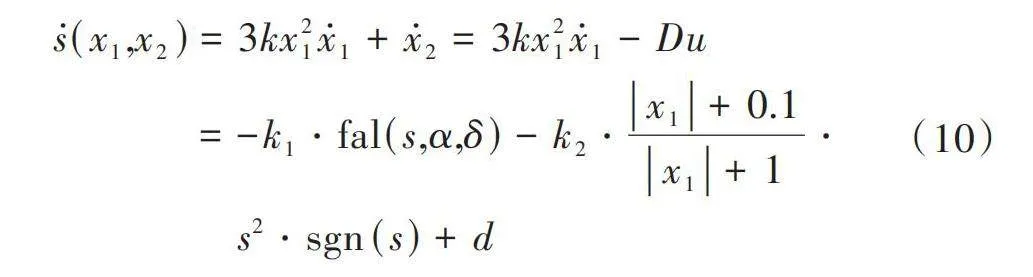
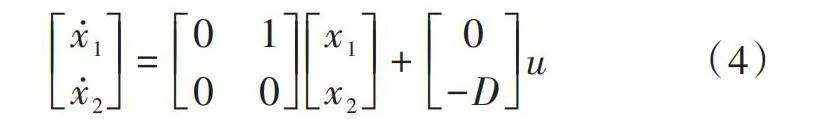
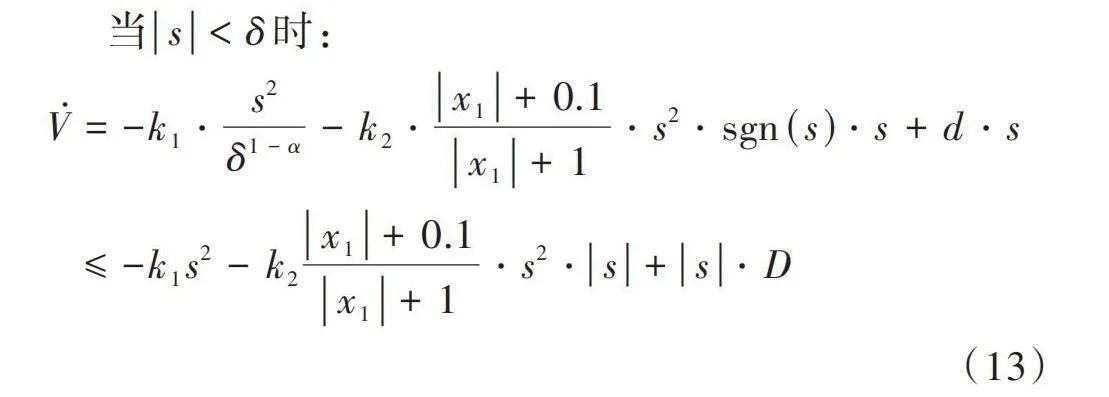
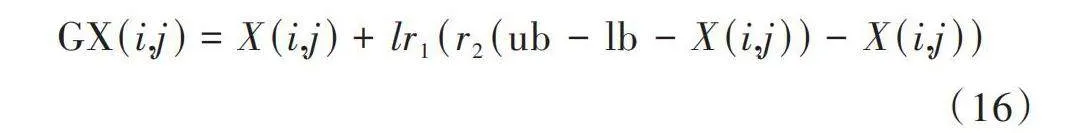
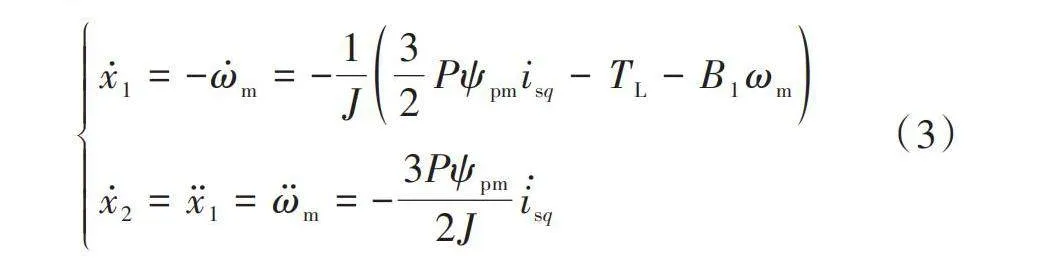
摘" 要： 針對傳統控制算法在農業機器人驅動電機速度控制方面存在的響應時間長、跟蹤效果差以及參數整定難度大，導致驅動電機轉速難以在短時間內收斂至預期值的問題，提出一種基于多策略改進的SMC?GTO電機速度跟蹤控制算法。首先，為了縮短驅動電機速度響應時間，提高速度跟蹤效果，設計了一種新型趨近率的改進滑模控制器（I?SMC）；其次，為了快速整定滑模控制器參數，引入了多策略改進的大猩猩部隊優化算法（MIGTO）。仿真結果表明： I?SMC能夠將電機運行過程中的動態誤差累計與過沖控制在0 rad/s內，并且可以在0.4 s內響應至預定速度。MIGTO算法在開發和探索階段均展現出卓越的性能，尤其在整定基于新型趨近率的改進滑模控制器參數工作中表現突出。該研究通過引入I?SMC和MIGTO算法，成功改進了驅動電機速度控制方式，有效縮短了響應時間，提升了速度跟蹤效果。

關鍵詞： SMC?GTO； 多策略改進； 速度跟蹤； 農業機器人； 驅動電機； 參數整定

中圖分類號： TN820.4?34； TP391.9； TP273" " " " " " " " " 文獻標識碼： A" " " " 文章編號： 1004?373X（2024）16?0069?07

SCM?GTO motor speed tracking control based on multi?strategy enhancement

YUE Fan， AIERKEN·Hamudula， ZHENG Weiqiang

（College of Mechanical Engineering， Xinjiang University， Urumqi 830017， China）

Abstract： In allusion to the problems of long response time， poor tracking effect， and difficult parameter tuning in traditional control algorithms for agricultural robot drive motor speed control， which make it difficult for the drive motor speed to converge to the expected value in a short time， a SMC?GTO motor speed tracking control algorithm based on multi?strategy enhancement is proposed. In order to shorten motor speed response time and enhance tracking effect， an improved sliding mode controller （I?SMC） with a novel approach rate is proposed. In order to realize the swift parameter tuning of the sliding mode controller， a multi?strategy improved gorilla troop optimization （MIGTO） algorithm is introduced. The simulation results reveal that the I?SMC can effectively constrain cumulative dynamic errors and overshooting within 0 rad/s during motor operation， achieving a response to the set speed within 0.4 s. The MIGTO algorithm can demonstrate exceptional performance in both development and exploration stages， particularly excelling in tuning parameters for the improved sliding mode controller with the novel approach rate. This study can successfully improve the speed control mode of the drive motor by introducing I?SMC and MIGTO algorithm， effectively shortening response time and improving speed tracking effect.

Keywords： SMC?GTO; multi?strategy enhancement; speed tracking; agricultural robot; drive motor; parameter tuning

0" 引" 言

對農業機器人驅動電機速度的精確控制是實現農機平穩自動運行的關鍵技術[1]。而永磁同步電機由于其高效節能、可靠性強和控制精度高的特點，在農業和工業場景中被廣泛使用。一方面，永磁同步電機采用數字控制技術，能夠實現高效管理，提高轉換效率和精度；另一方面，永磁同步電機可以精確控制轉速，滿足農業機械在不同作業條件下的需求[2]。此外，永磁同步電機采用無觸點結構，不存在機械磨損和摩擦，從而減少維修和更換成本，提高農業機械的使用壽命[3]。因此，永磁同步電機非常適用于執行農田中的播種、施肥與灌溉等作業任務。在農田中執行農業生產作業時，頂層路徑規劃系統向永磁同步電機分配速度控制信號，因此高精度速度控制對于實現理想規劃的等距作業至關重要[4]。

傳統的控制策略無法滿足農業機器人驅動電機在復雜農田環境下的速度響應要求，而滑模變結構控制（Sliding Mode Controller， SMC）是一種適用于非線性多變量強耦合系統的控制策略，該方法在實際使用中表現出了獨特的優越性[5]。目前的研究大多針對農業機器人中永磁同步電機速度控制的快速性、準確性和魯棒性，采用滑模控制取代傳統的PI控制[6]。例如，崔紅等設計了一種基于滑模變結構的無傳感器直接轉矩控制，減小了定子電流和電磁轉矩的脈動[7]。武志濤等設計了一種復合式滑模位置控制方法，將定結構滑模控制器和擴展滑模擾動器相結合，提高滑模滑動品質的同時保證了位置追蹤的精度[8]。沈毓駿等提出了一種基于滑模觀測器改進的DTC算法，在仿真中實現了較好的動態性能和抗干擾能力[9]。黃成成等提出了一種二階Super?twisting滑模理論，該方法有效削弱了滑模抖振，提高了系統的估算精度和響應速度[10]。然而，上述方案中針對控制器參數的整定通常是基于經驗選擇或者不斷試錯而得出的。本文針對傳統控制策略響應時間長、跟蹤效果差的問題，提出了一種新型趨近率的改進滑模控制器，用于實現永磁同步電機在農田運行環境中的高品質速度跟蹤。其次，為了實現控制器參數的快速整定，引入了改進的人工大猩猩算法對控制器參數進行整定。最后，通過在永磁同步電機實驗平臺上進行對比實驗，驗證了新方案相對于傳統方案的有效性。

1" 永磁同步電機的數學模型

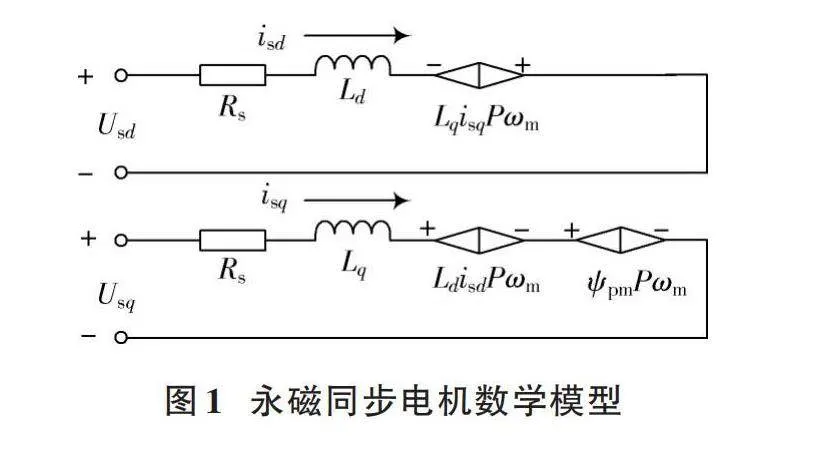
在永磁同步電機[d?q]軸轉子坐標系中，可將其簡化為如圖1所示的電路模型[11]。

根據圖1中永磁同步電機的電路模型可得表貼式永磁同步電機在[d?q]坐標下的電壓方程[12]，如式（1）所示。

[Usd=Rsisd+Lddisddt-LqisqPωmUsq=Rsisq+Lqdisqdt+LdisdPωm+ψpmPωmJdωmdt=32P[isd（Ld-Lq）+ψpm]isq-TL-B1ωm] （1）

式中：[Us*]、[Rs]、[is*]、[L*]分別代表各軸的定子電壓、電阻、電流、電感；[P]為極對數；[J]為轉動慣量；[TL]為轉矩負載；[ψpm]為永磁鐵磁鏈；[B1]為黏滯摩擦系數；[ωm]為電機機械角速度。

理想情況中，表貼式永磁同步電機的定子電流完全用于電磁轉矩做功，即[isd=0]，且[Ld=Lq=L]，故由式（1）可得：

[Ldisqdt=Usq-ψpmPωm-RsisqJdωmdt=32Pψpmisq-TL-B1ωm] （2）

在式（2）中選取狀態變量[dωm=x1=ωg-ωm]，[x2=x1=-ωm]，將其黏滯摩擦因數視為常數，其中[ωg]為目標角速度，并對兩邊[q]軸電流同時進行求導，如式（3）所示。

[x1=-ωm=-1J32Pψpmisq-TL-B1ωmx2=x1=ωm=-3Pψpm2Jisq] （3）

在式（3）中令[u=isq]，[D=（3Pψpm）（2J）]， 可以建立永磁同步電機的狀態空間表達式，如式（4）所示。

[x1x2=0100x1x2+0-Du] （4）

2" 速度閉環控制器設計

2.1" 速度控制器設計

傳統的滑模控制器可能會存在兩個缺點：一是系統收斂速度過慢；二是其在期望點附近抖振嚴重。針對這兩個問題，本文提出了一種改進的新型趨近率[13?14]的滑模控制器（Improved Sliding Mode Controller），其表達式如式（5）所示。

[s=-k1?fal（s，α，δ）-k2?x1+0.1x1+1?s2?sgn（s）+d] （5）

式中[fal（s，α，δ）]定義如式（6）所示。在[s≥δ]時，采用指數趨近率，加速收斂的同時減少穩定時間；在[slt;δ]時，采用[sδ1-α]來消除系統抖振。第二項中[x1]為系統變量，用來減少系統抖振。第三項[d]用于消除系統中不確定的有界擾動。

[fal（s，α，δ）=sβ?s，s≥δsδ1-α，" "slt;δ] （6）

[β=2?a?sgn（s-1）-1] （7）

[sgn（s）=1，" sgt;0-1，s≤0] （8）

進一步說明在初始搜索狀態中給定[k1=1]、[k2=1]、[δ=1]、[α=1]、[a=0.5]、[d=0]。

在綜合考量趨近速率與抗干擾能力的情況下，本文采用曲線滑模面函數，如式（9）所示。

[s（x1，x2）=kx31+x2] （9）

對式（9）求導可得：

[s（x1，x2）=3kx21x1+x2=3kx21x1-Du" " " " " " " "=-k1?fal（s，α，δ）-k2?x1+0.1x1+1?" " " " " " " " " " s2?sgn（s）+d] （10）

進一步可得：

[iq=1Dudt=1D3kx21x1+k1?fal（s，α，δ）+" " " "k2?x1+0.1x1+1?s2?sgn（s）-ddt] （11）

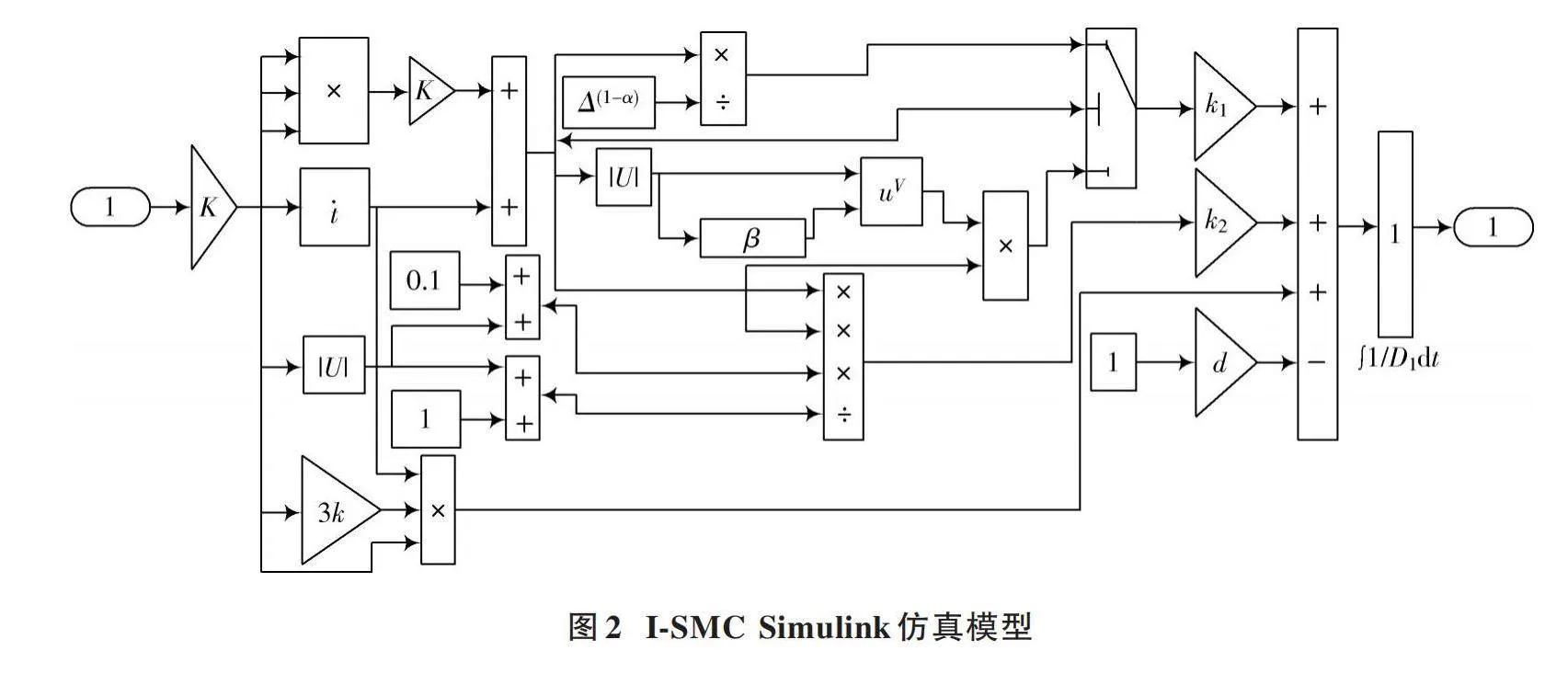
由式（11）可得對[q]軸電流控制的I?SMC的Simulink模型，如圖2所示。

2.2" 穩定性分析

選取Lyapunov函數[V=12s2]，對其求導得[V=s?s]，將式（5）代入可得如下公式。

當[s≥δ]時：

[V=-k1?sβ+2-k2?x1+0.1x1+1?s2?sgn（s）?s+d?s≤-（k1+k2）s2+β+s?D] （12）

即當[（k1+k2）s1+β≥D]時可以滿足[V≤0]，系統穩定。

當[slt;δ]時：

[V=-k1?s2δ1-α-k2?x1+0.1x1+1?s2?sgn（s）?s+d?s≤-k1s2-k2x1+0.1x1+1?s2?s+s?D] （13）

進一步可得：

[V+k1s2=V+2?k1?V" " " " " " " " ≤-k2x1+0.1x1+1?s2?s+s?D] （14）

[s≥D（x1+1）k2（x1+0.1）] （15）

根據文獻[15]，系統在有限時間內收斂，并且區域[s≥10?Dk2]是有限時間收斂區域，即存在[s≤10?Dk2]的誤差邊界。綜上所述可得[V=s?s≤0]，系統穩定。

3" 改進人工大猩猩部隊優化算法

3.1" 動態反向變異初始化

在處理實際工程問題時，人工大猩猩部隊優化算法（Artificial Gorilla Troops Optimizer， GTO）通常采用隨機生成初始數據，這樣初始化生成的種群不能滿足隨機分布，從而降低了種群的多樣性。針對該問題，本文利用動態反向變異初始化[16]的隨機性與逆向性來增加GTO初始化種群的多樣性，減少其陷入局部最優的可能，提高了全局探索能力。動態反向變異初始化模型生成初始化種群序列的數學表達式如式（16）所示。

[GX（i，j）=X（i，j）+lr1（r2（ub-lb-X（i，j））-X（i，j））] （16）

式中：[X（i，j）]為更新前的大猩猩位置；[GX（i，j）]為更新后的大猩猩位置；[ub]、[lb]分別為搜索空間上下限；[r1]、[r2]是[0]和[1]之間的隨機數；權重因子參數[l=2]。

3.2" 小孔成像反向學習策略

原始GTO算法對大猩猩位置的更新策略是基于銀背大猩猩位置更新當前大猩猩位置。然而，當銀背大猩猩處于局部最優解時，種群的多樣性減少，導致算法極易陷入局部最優，特別是在求解高階優化問題時尤為突出。為克服該問題，本文提出了采用小孔成像反向學習策略[17]來產生新個體。該策略通過將原始個體在搜索空間內進行反向映射得到新個體，有助于跳出局部最優并加速搜索。該策略的數學表達式如式（17）所示。[GX（i，j）=ub+lb2+ub+lb2m-X（i，j）m] （17）

[m=1-3?ItIt，max128] （18）

式中：[m]為縮放因子；[It]為當前迭代次數；[It，max]為最大迭代次數。

3.3" 黃金正弦策略

在人工大猩猩算法的整個探索階段中，加快收斂速度可以提高算法的整體效率。為此，本文引入黃金正弦策略[18]，如式（19）所示。該策略利用正弦函數與圓的關系，能夠訪問到正弦函數的所有值，并在位置迭代更新過程中引入黃金分割數，從而縮小解決問題的搜索空間，提高搜索速度，實現了探索和開發的良好平衡。

[GX（i，：）=X（i，：）?sin r3-r2?sin r3?" " " " " " " " " " m1?Xs-m2?X（i，：）] （19）

[m1=j?（1-λ）+k?λ] （20）

[m2=j?λ+k?（1-λ）] （21）

式中：[Xs]是銀背大猩猩的空間位置；[j]是[0]～[π]之間的隨機數；[k]是[0]～[-π]之間的隨機數；[r3]是[0]～[1]之間的隨機數；[λ]取[5-12]。

3.4" MIGTO算法流程

綜合上述改進方法，本文提出的MIGTO算法流程如下。

步驟1：輸入種群大小[N]，最大迭代次數[It，max]，搜索維度[D]，搜索邊界[ub]、[lb]，以及參數[β]、[p]、[w]、[l]和[λ]。

步驟2：初始化大猩猩個體的空間位置[Xi]和適應度值[F（Xi）]，根據種群中個體適應度值選取銀背大猩猩[Xs]并記錄其適應度值[F（Xs）]，其中[i=1，2，…，N]。

步驟3：采用動態反向變異初始化策略初始化種群。

步驟4：根據步驟3優化后的種群[GXi]，按照大猩猩個體適應度排序，選取銀背大猩猩[Xs]并記錄其適應度值[F（Xs）]。

步驟5：利用黃金正弦策略加快種群中其他個體對銀背大猩猩的跟蹤，并根據式（20）、式（21）更新參數[m1]、[m2]。

步驟6：根據步驟5迭代后的種群[GXi]，按照當前種群中大猩猩個體適應度排序，選取銀背大猩猩[Xs]并記錄其適應度值[F（Xs）]。

步驟7：根據式（17）對進入探索階段的大猩猩位置進行反向映射，并根據式（18）更新參數[m]。

步驟8：根據步驟7反向映射后的種群[GXi]，按照大猩猩個體適應度排序，選取銀背大猩猩[Xs]，并記錄其適應度值[F（Xs）]。

步驟9：判斷當前迭代次數[It]是否大于最大迭代次數[It，max]，若不符合此條件，則繼續執行步驟5；若滿足此條件，則終止迭代并輸出最優位置和最佳適應度值，即銀背大猩猩位置[Xs]和銀背大猩猩適應度值[F（Xs）]。

3.5" MIGTO算法仿真實驗

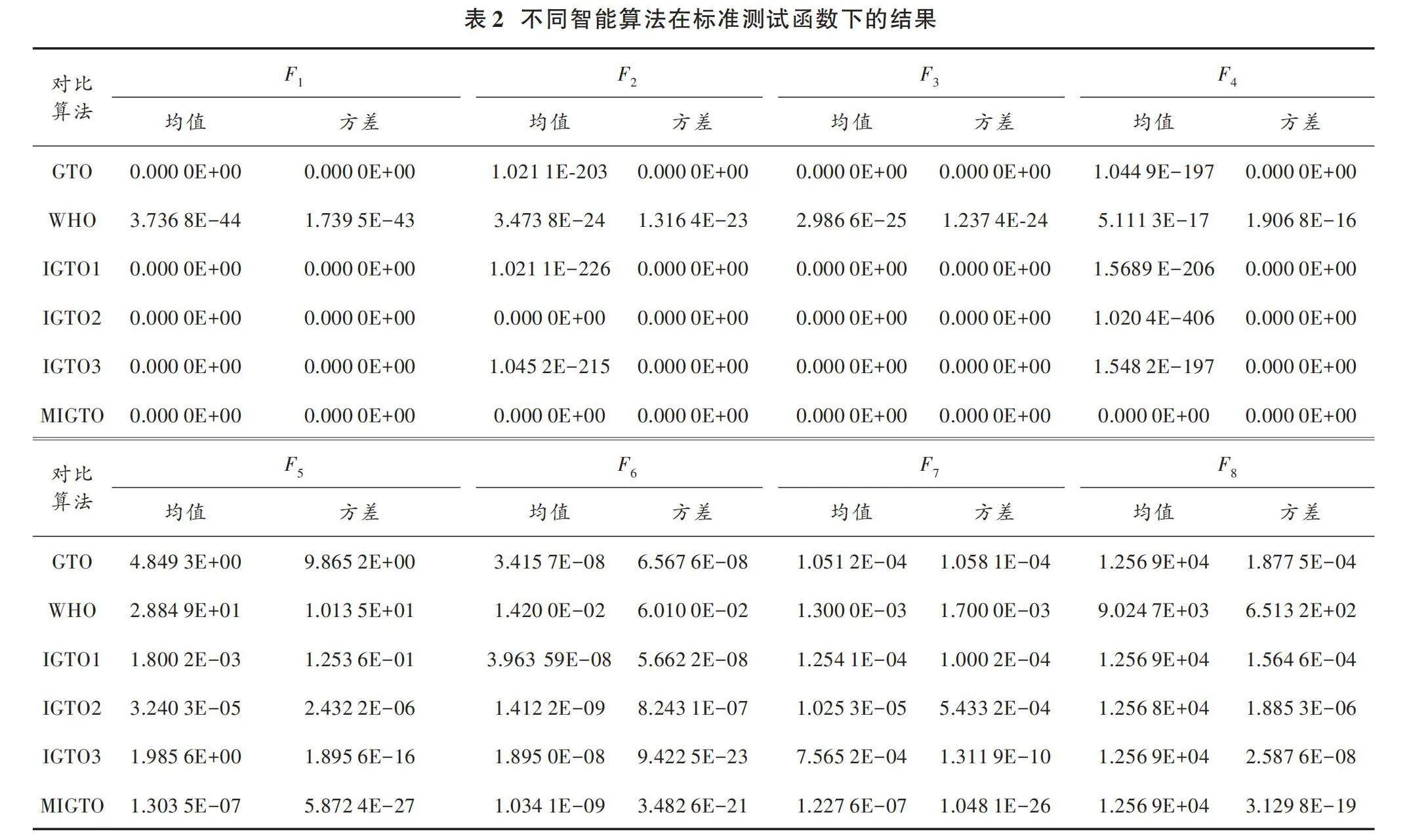
為了進一步評價本文提出的MIGTO算法性能，選取CEC2017測試標準中前8個測試函數，并選取GTO、WHO[19]、IGTO1[20]、IGTO2[21]、IGTO3[22]這5種較為優秀的算法進行對比試驗。每種算法測試參數如表1所示。每次實驗均采用相同的實驗參數，即種群規模[N=30]，種群維數[D=30]，最大迭代次數[It，max=500]，每種算法獨立運行100次并記錄結果。仿真環境的硬件配置為Windows Server（2025）操作系統，CPU為Intel[?] CoreTM i7?11700KF CPU@3.60 GHz處理器，32 GB內存。仿真環境的軟件配置為Matlab R2022a。算法仿真結果如表2所示。

3.6" MIGTO算法精度分析

標準測試函數CEC2017在實驗中的均值與標準差可以直觀衡量改進算法的精確性與穩定性。因此，其可以衡量MIGTO算法的有效性。

3.6.1" 開發性能評估

表2中標準測試函數的平均值和標準差可以反映出MIGTO的優化精度和收斂穩定性。在函數[F1]、[F2]、[F3]和[F4]優化問題中，MIGTO算法能夠穩定且快速地找到理論最優值0，且算法適應度的平均值和方差均優于其他3種較優的GTO算法與WHO算法。綜合上述分析可知：由于MIGTO算法在初始化種群階段引入了動態反向變異初始化，因此增加了新種群的隨機性；并進一步引入了黃金正弦策略，幫助算法在種群內部進行大規模搜索時加快收斂速度。這反映了MIGTO具有較好的收斂性，在前期開發時能力占優。

3.6.2" 探索性能評估

在函數[F5]、[F6]、[F7]和[F8]的優化問題中，MIGTO算法的均值和標準差依然優于其他測試算法，并且在測試結果精度較優的情況下，測試結果穩定性也超過其他3種較優的GTO算法與WHO算法幾個數量級。綜合分析表明，由于本文引入了小孔成像反向學習策略，相較于其他的對照算法，當MIGTO算法迭代中出現多個局部最優解時，尤其是優化復雜多峰函數時，它并沒有過早地進行收斂，并且依然可以實現優于其他對照算法的效果。這證明了MIGTO算法在收斂過程中的準確性與穩定性。

4" 基于MIGTO的滑模控制器參數整定

為驗證本文所提算法的準確性與有效性，采用Matlab R2022a搭建了基于永磁同步電機的Simulink仿真環境，該仿真主要實現以下目的：驗證設計的基于新型趨近率的滑模控制器的性能與穩定性，并與傳統控制器控制結果進行比較；驗證MIGTO算法相較于其他3種較優GTO算法和WHO算法在基于新型趨近率的滑模控制器參數整定過程中的優勢。

4.1" 滑模控制器參數整定環境搭建

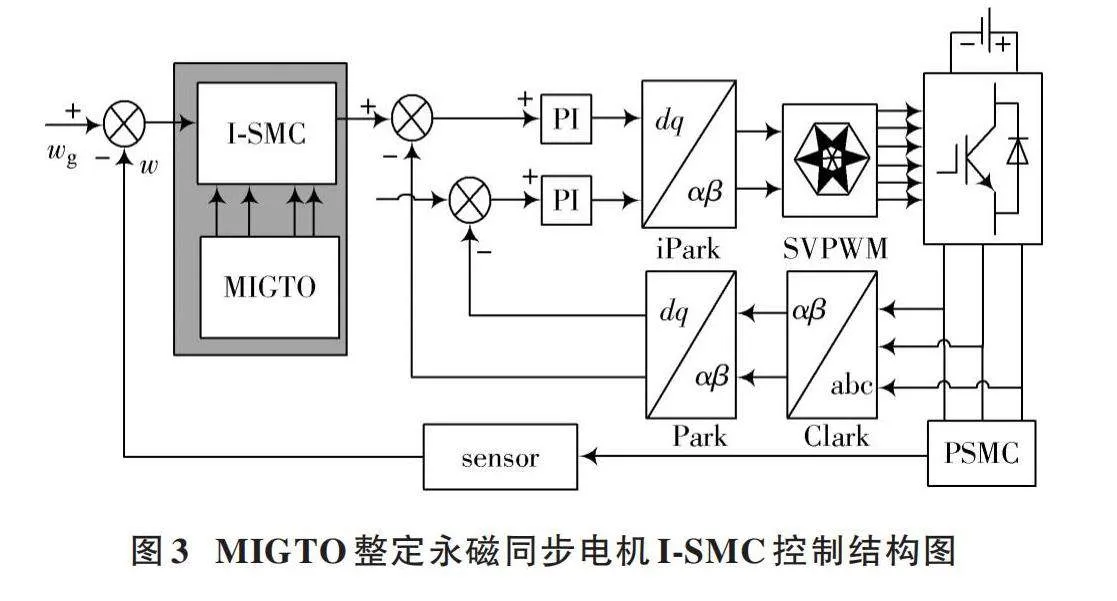
本文將永磁同步電機速度控制仿真模型[23]進行簡化，如圖3所示。通過應用群智能算法對改進的滑模控制器中的參數進行整定，實現了對電機速度的快速、準確控制。該模型簡化了電機速度控制的復雜性，使得研究人員能夠更加專注于控制算法的性能優化。通過使用群智能算法進行參數整定，能夠提高電機速度控制的穩定性和響應速率，從而實現更好的控制效果。

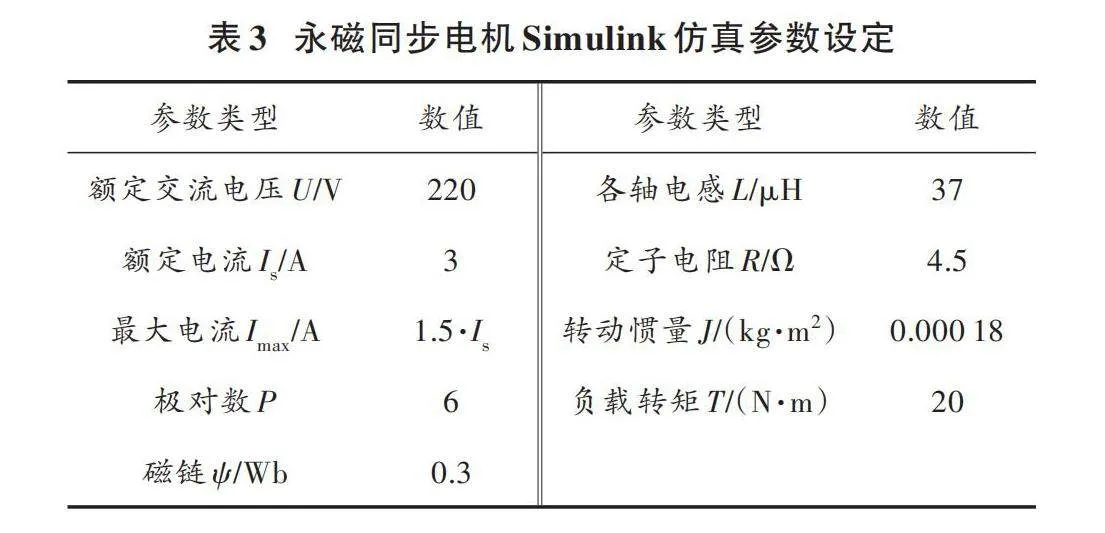
仿真模型中參數設置如表3所示。

4.2" I?SMC控制器的速度跟蹤仿真實驗

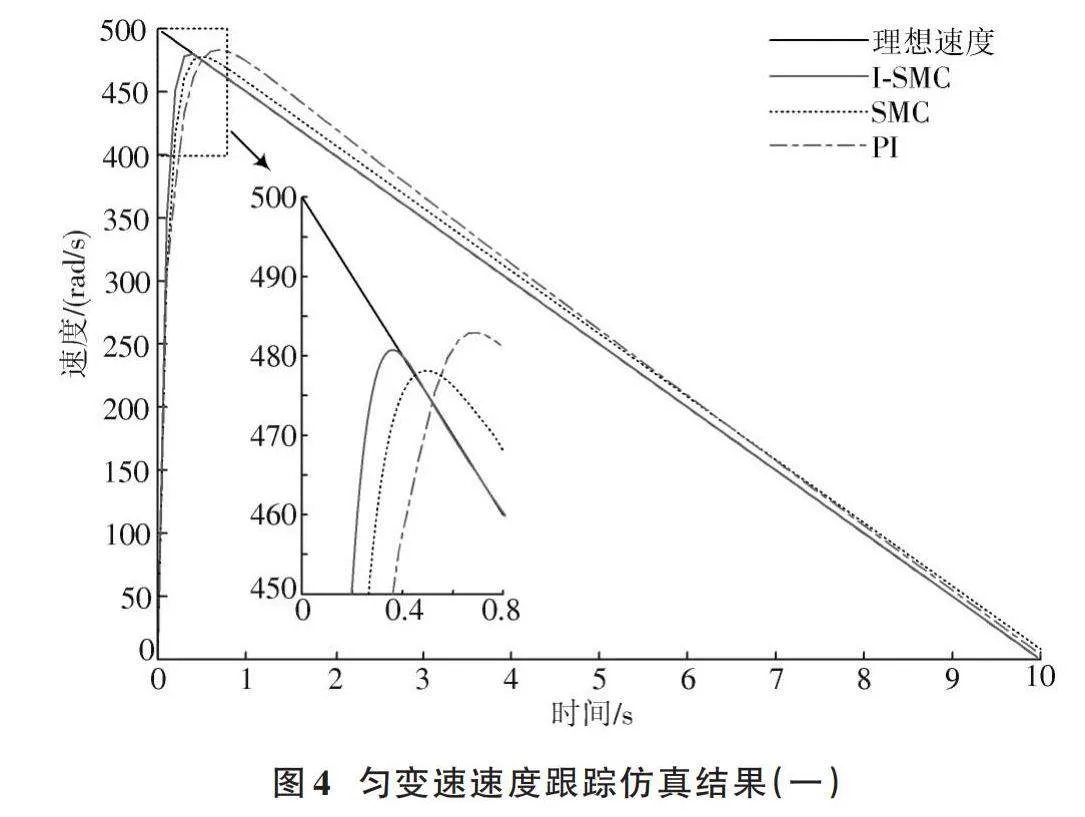
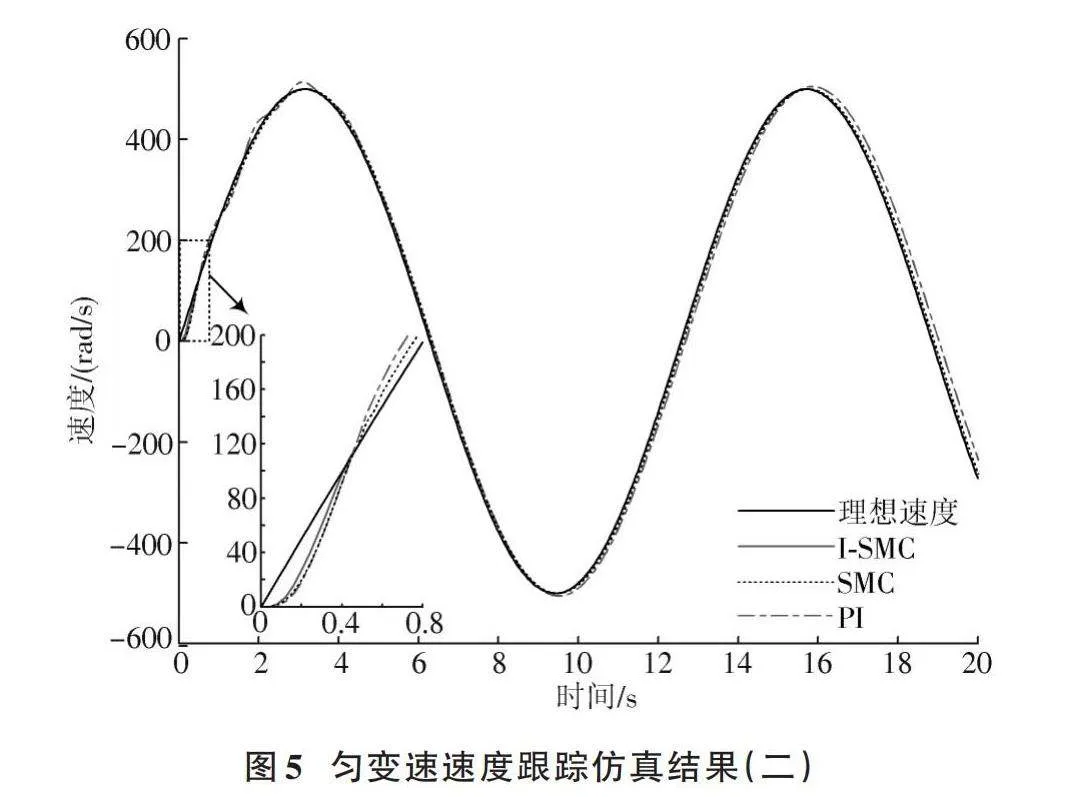
為驗證本文所提出的I?SMC控制器在永磁同步電機速度跟蹤中的優勢，將I?SMC與未改進的SMC和傳統PI控制器的速度跟蹤效果進行比較。本次實驗中三種控制算法均使用MIGTO進行參數整定，模擬永磁同步電機在實際使用中速度的勻變速情況和周期變化情況。利用Simulink進行仿真的結果如圖4、圖5所示。

從圖4中可以看出，對于初始速度為500 rad/s并以50 rad/s的速率進行遞減的勻變速運動，未改進的SMC控制器相比于傳統的PI控制器可以在更短時間內收斂到預定速度，但這兩種控制器均存在較大的系統誤差；而本文提出的I?SMC控制器在實現收斂速度提升的同時也消除了系統誤差，保證了速度跟蹤的效果。

從圖5中可以看出：對于初速度為0 rad/s、最大速度為500 rad/s、周期為9.5 s的周期變化運動，相比于傳統的PI控制器和未改進的SMC控制器，本文提出的I?SMC控制器幾乎不存在系統誤差；并且相比于未改進的SMC控制器，本文提出的I?SMC控制器可以在0.42 s內收斂，且超調量和系統誤差均趨近于0 rad/s。

綜合分析上述結論可知，在同時采用MIGTO算法對永磁同步電機速度控制器參數進行整定的情況下，本文提出的I?SMC算法相比于未改進的SMC算法和傳統的PI算法，響應速度更快，跟蹤效果更好，能夠實現更好的控制效果。

4.3" 智能算法整定I?SMC參數實驗

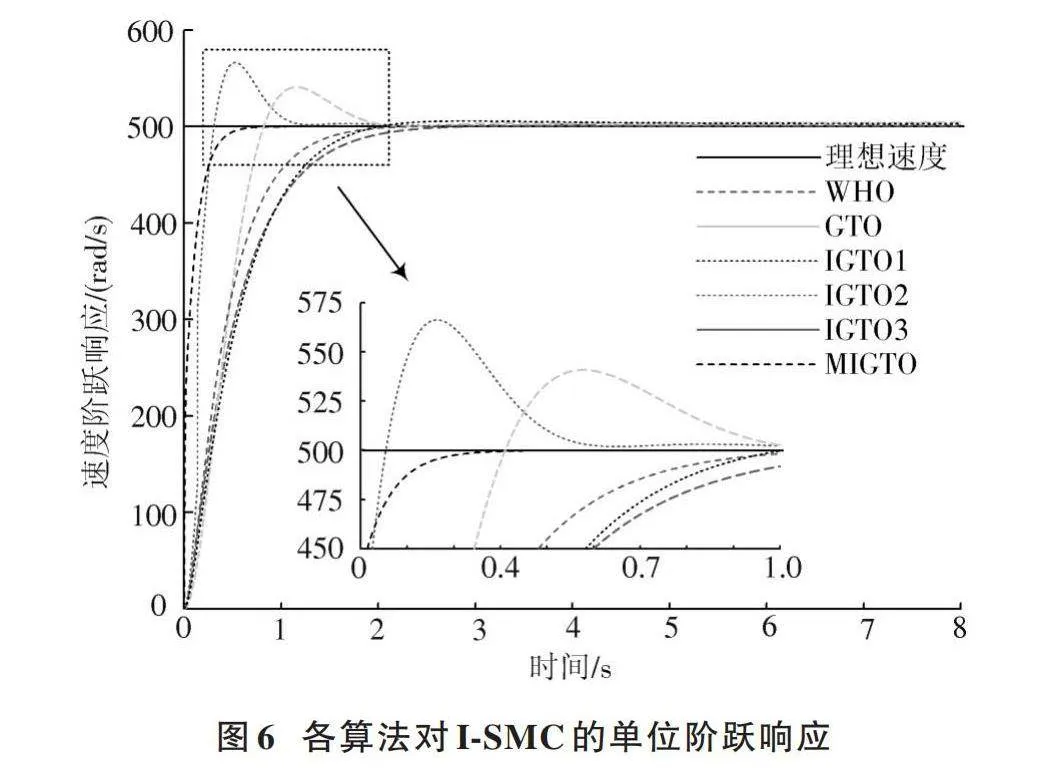
為了評估MIGTO算法在控制器參數整定方面的高效性，本文選擇改進的滑模控制器作為測試對象，采用MIGTO算法以及其他智能算法，包括GTO、IGTO1、IGTO2、IGTO3和WHO進行對比，并對I?SMC的7個參數進行整定，得到了不同智能算法在參數整定方面的測試結果。利用Simulink得到的仿真結果如圖6所示。

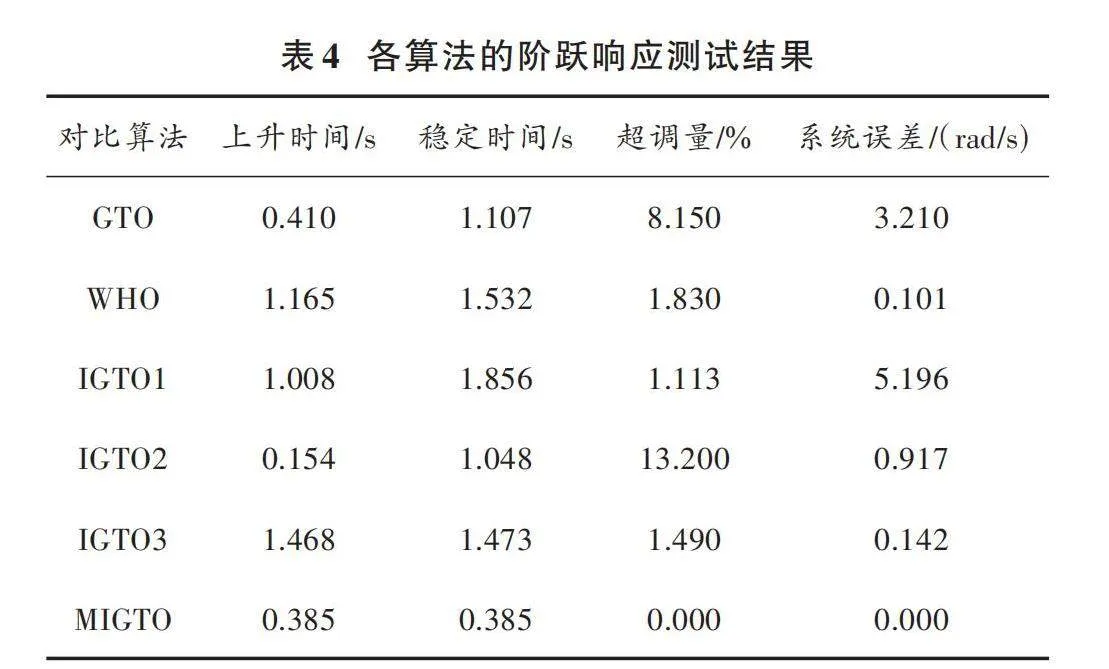
各算法的階躍響應測試結果如表4所示。

由表4可知，在對I?SMC參數進行整定的過程中，原始GTO算法相比于采用多種改進策略的IGTO算法在上升時間和超調量方面均有不足之處。IGTO1算法相比于其他兩種IGTO算法在上升時間方面有顯著優勢，但超調量與系統誤差均過大。相比之下，WHO算法在超調量與系統誤差方面表現均較優，但是上升時間過長；然而，MIGTO算法表現出最短的上升時間（0.385 s）、最高的收斂精度（0 rad/s）和最優的穩定性（0），同時在允許的上升時間內達到穩定狀態，滿足實際使用中的要求。這證明了MIGTO算法在控制器參數整定方面的顯著優勢，為實際應用提供了可靠的控制策略。

5" 結" 論

本文提出了一種多策略改進的大猩猩部隊優化算法（MIGTO），并將其與改進的滑模控制器相結合，建立了一個約束優化模型，旨在搜索最優的滑模控制器參數。通過選擇相對優秀的另外3種GTO算法和WHO算法，以及結合標準測試函數驗證結果和復雜仿真場景下的滑模控制器參數整定效果，可得出以下結論。

1） 針對傳統GTO算法整定滑模控制器參數的缺陷，本文所提MIGTO算法引入動態反向變異初始化、小孔成像反向學習策略和黃金正弦策略。在平衡滑模控制器參數整定過程中，提升了算法的收斂速度與精度。

2） 與傳統的GTO算法、其他3種較優秀的GTO算法和WHO算法相比，在標準測試函數的尋優過程中，MIGTO算法具有良好的收斂效果和尋優精度，且滑模控制器參數整定中的4項指標均表現良好。由此可知，本文所改進的MIGTO算法在滑模控制器參數整定過程中的整定效率、收斂精度和尋優時間均優于其他算法。

注：本文通訊作者為艾爾肯·亥木都拉。

參考文獻

[1] 張云鶴，溫靖，林森，等.北京市設施農業機器人發展現狀及策略[J].農業工程技術，2023，43（2）：27?28.

[2] 顧家偉.外轉子永磁電機全運行范圍無位置傳感器矢量控制研究[D].沈陽：沈陽工業大學，2022.

[3] 李賡.基于改進超螺旋算法的永磁同步電機速度控制研究[D].桂林：桂林理工大學，2020.

[4] 張帥.基于GNSS的農田信息采集機器人點跟蹤控制系統研究[D].武漢：華中農業大學，2022.

[5] WANG Chengxuan， TANG Jiawei， JIANG Baoping， et al. Sliding?mode variable structure control for complex automatic systems： a survey [J]. Mathematical biosciences and engineering ： MBE， 2022， 19（3）： 2616?2640.

[6] 張永碩，王浩，周顯龍，等.永磁同步電機的改進型滑模變結構控制研究[J].機電元件，2021，41（3）：20?23.

[7] 崔紅，高有清.基于滑模變結構的高速同步電機直接轉矩控制[J].無線互聯科技，2023，20（12）：93?96.

[8] 武志濤，李帥，程萬勝.基于擴展滑模擾動觀測器的永磁直線同步電機定結構滑模位置跟蹤控制[J].電工技術學報，2022，37（10）：2503?2512.

[9] 沈毓駿，豐飛，邵瑛.基于滑模控制的改進直接轉矩控制算法研究[J].電工技術，2022（23）：32?35.

[10] 黃成成，金海，魯文其.基于Super?Twisting無位置滑膜觀測器的永磁同步電機控制[J].電子科技，2023，36（11）：8?13.

[11] 包西平，王毅，張博洋，等.車載永磁同步電機精確數學模型構建及仿真研究[J].機電工程技術，2022，51（11）：181?185.

[12] 焦子躍.基于模糊分數階PID的永磁同步電機速度控制研究[D].石家莊：河北科技大學，2021.

[13] XU F， AN N， MAO J L， et al. A new variable exponential power reaching law of complementary terminal sliding mode control [EB/OL]. [2023?01?24]. https：//ideas.repec.org/a/hin/complx/8874813.html.

[14] WANG Xiaojing， BAI Bocheng， FENG Yaming. Friction feedforward compensation composite control of continuous rotary motor with sliding mode variable structure based on an improved power reaching law [J]. Electronics， 2023， 12（6）： 1447.

[15] MARKS G M， SHTESSEL Y， GRATT H， et al. Effects of high order sliding mode guidance and observers on hit?to?kill interceptions [C]// AIAA Guidance， Navigation， amp; Control Conference amp; Exhibit. San Francisco： AIAA， 2006： 5967.

[16] CAO Di， XU Yunlang， YANG Zhile， et al. An enhanced whale optimization algorithm with improved dynamic opposite learning and adaptive inertia weight strategy [J]. Complex amp; intelligent systems， 2023， 9（1）： 767?795.

[17] 龍文，伍鐵斌，唐明珠，等.基于透鏡成像學習策略的灰狼優化算法[J].自動化學報，2020，46（10）：2148?2164.

[18]" DUAN Yuxian， LIU Changyun， LI Song， et al. Gaussian perturbation specular reflection learning and golden?sine?mechanism?based elephant herding optimization for global optimization problems [J]. Computational intelligence and neuroscience， 2021， 2021： 9922192.

[19] NARUEI I， KEYNIA F. Wild horse optimizer： a new meta?heuristic algorithm for solving engineering optimization problems [J]. Engineering with computers， 2021， 38（S4）： 3025?3056.

[20] LIANG Qingwei， CHU Shuchuan， YANG Qingyong， et al. Multi?group gorilla troops optimizer with multi?strategies for 3D node localization of wireless sensor networks [J]. Sensors， 2022， 22（11）： 4275.

[21] GHITH E S， TOLBA F A A. Tuning PID controllers based on hybrid arithmetic optimization algorithm and artificial gorilla troop optimization for micro?robotics systems [J]. IEEE access， 2023， 11： 27138?27154.

[22] SINGH N K， GOPE S， KOLEY C， et al. Optimal bidding strategy for social welfare maximization in wind farm integrated deregulated power system using artificial gorilla troops optimizer algorithm [J]. IEEE access， 2022， 10： 71450?71461.

[23] ZOU Quan， LI Xiaoxiang， CHEN Dong. Observer based sliding mode control of PMSM speed regulation system with a novel reaching law [J]. IET power electronics， 2022， 15（10）： 886?900.