改進關聯策略的三維多目標跟蹤算法

摘" 要： 為提高基于激光雷達的三維多目標跟蹤準確度，提出一種基于檢測的3D多目標跟蹤算法。使用深度神經網絡從激光點云中獲取目標的位置信息后，對目標跟蹤算法中的關聯策略進行了優化。首先，估計出目標的速度信息，與位置信息一同納入觀測值，在BEV視角下使用卡爾曼濾波器對目標的狀態進行預測與更新；然后，基于目標與激光雷達的距離來評估目標位置的不確定度，用于修正觀測模型中的協方差矩陣；最后，在馬氏距離中添加對目標測量的不確定性加權項，使用匈牙利算法進行數據關聯。在大規模自動駕駛數據集Nuscenes上對所提算法進行了測試，得出其跟蹤精度超過了現有的基線方法。消融實驗結果表明，所提出的改進措施能有效提高三維多目標跟蹤的性能。

關鍵詞： 三維多目標跟蹤； 關聯策略； 激光雷達點云； 不確定度評估； 卡爾曼濾波器； 協方差矩陣； 馬氏距離； 匈牙利算法

中圖分類號： TN958.98?34； TP391" " " " " " " " " "文獻標識碼： A" " " " " " " " " 文章編號： 1004?373X（2024）16?0085?05

3D multi?object tracking algorithm with improved association strategy

YI Kefu1， WEN Zhaocheng2， HU Rongdong3

（1. College of Automotive and Mechanical Engineering， Changsha University of Science amp; Technology， Changsha 410000， China;

2. School of Traffic and Transportation Engineering， Changsha University of Science amp; Technology， Changsha 410000， China;

3. Changsha Intelligent Driving Institute Co.， Ltd.， Changsha 410208， China）

Abstract： In order to enhance the accuracy of three?dimensional （3D） multi?object tracking based on lidar， a detection?based 3D multi?target tracking algorithm is proposed. After using deep neural networks to obtain target position information from lidar point clouds， the correlation strategy in the target tracking algorithm is optimized. The velocity information of the target is estimated and incorporated into the observations along with the position information. A Kalman filter is used to predict and update the target states in the bird's eye view （BEV） perspective. The uncertainty of target position is evaluated based on the distance between the target and lidar， which is used to correct the covariance matrix in the observation model. An uncertainty weighting term for target measurement is introduced into the Mahalanobis distance， and the Hungarian algorithm is utilized for the data association. The proposed algorithm was tested on the large?scale autonomous driving dataset Nuscenes， and it was found that its tracking accuracy exceeded existing baseline methods. The results of the ablation experiments indicate that the proposed improvement measures can effectively improve the performance of 3D multi?object tracking.

Keywords： 3D multi?object tracking; association strategy; lidar point cloud; uncertainty assessment; Kalman filter; covariance matrix; Mahalanobis distance; Hungarian algorithm

0" 引" 言

激光雷達點云多目標跟蹤方法可以劃分為基于端到端的跟蹤方法和基于檢測的跟蹤方法。前者無需人工干預就可以取得不錯的跟蹤效果，但需要大量數據且耗費大量計算資源[1?2]。基于檢測的跟蹤方法[3?4]需要選定合適的目標檢測器、運動模型和關聯策略，相對于基于端到端的跟蹤方法來說，基于檢測的跟蹤方法易于解耦且更依賴于先驗的運動規律，對處理遮擋等情況更為有效，且具有實時性高、可解釋性好的特點，更符合實際道路行駛的要求。

基于檢測的跟蹤方法通常使用卡爾曼濾波方法來對目標進行預測。以往的方法大多聚焦于對運動模型和關聯方法的改進[4?5]，而忽視了對于觀測信息的充分利用；且這些方法通常僅將目標的位置信息作為觀測值而放棄使用速度信息。但隨著檢測器的越發完善，檢測出的速度信息越發準確，速度信息將成為濾波過程中的重要矯正信息。同時，激光雷達點云的特性導致遠距離點云稀疏，因此距離激光雷達越遠的目標的檢測置信度越低，即目標的位置信息和速度信息的不確定度越大。通過目標與激光雷達的距離計算出目標信息的不確定度并將其納入濾波預測過程以及數據關聯過程，可以有效減少點云稀疏性為目標跟蹤過程帶來的負面影響。

針對上述問題，本文提出了一種基于檢測的點云多目標跟蹤算法。利用神經網絡檢測器從點云數據中提取目標在BEV視角下的位置信息，并結合前后幀數據計算目標速度；采用恒速卡爾曼濾波模型預測航跡狀態，并依據觀測模型得到該航跡的預測測量值。最后，通過計算當前幀檢測測量值與上一幀航跡預測測量值的馬氏距離，構建損失矩陣，并利用匈牙利匹配算法實現檢測與航跡的數據關聯。為增強跟蹤算法的準確性和魯棒性，本文對跟蹤算法進行了三個關鍵改進。

1） 在觀測模型中引入速度信息作為測量值，使得跟蹤更為穩定。

2） 根據目標與激光雷達的距離估計檢測目標的位置不確定度，進而計算觀測模型的測量協方差矩陣，提高了跟蹤的準確性。

3） 采用馬氏距離代替常用的IoU作為航跡與檢測間的距離度量，有效地避免了檢測與航跡的不確定性。

通過消融實驗驗證，本文方法在處理復雜場景下的3D多目標跟蹤任務中展現出了優越的性能，尤其在處理目標遮擋、交叉等復雜情況時，表現出了明顯的優勢。

1" 3D多目標跟蹤系統設計

本文提出的NU3DMOT算法由以下三個部分組成。

1） 從基于神經網絡的3D目標檢測器中獲取檢測結果，并將檢測結果以點的方式呈現。

2） 通過改進的恒速模型卡爾曼濾波器對目標進行預測以及更新。

3） 進行分層數據關聯，并結合手動調整的生命周期管理系統對航跡進行管理。

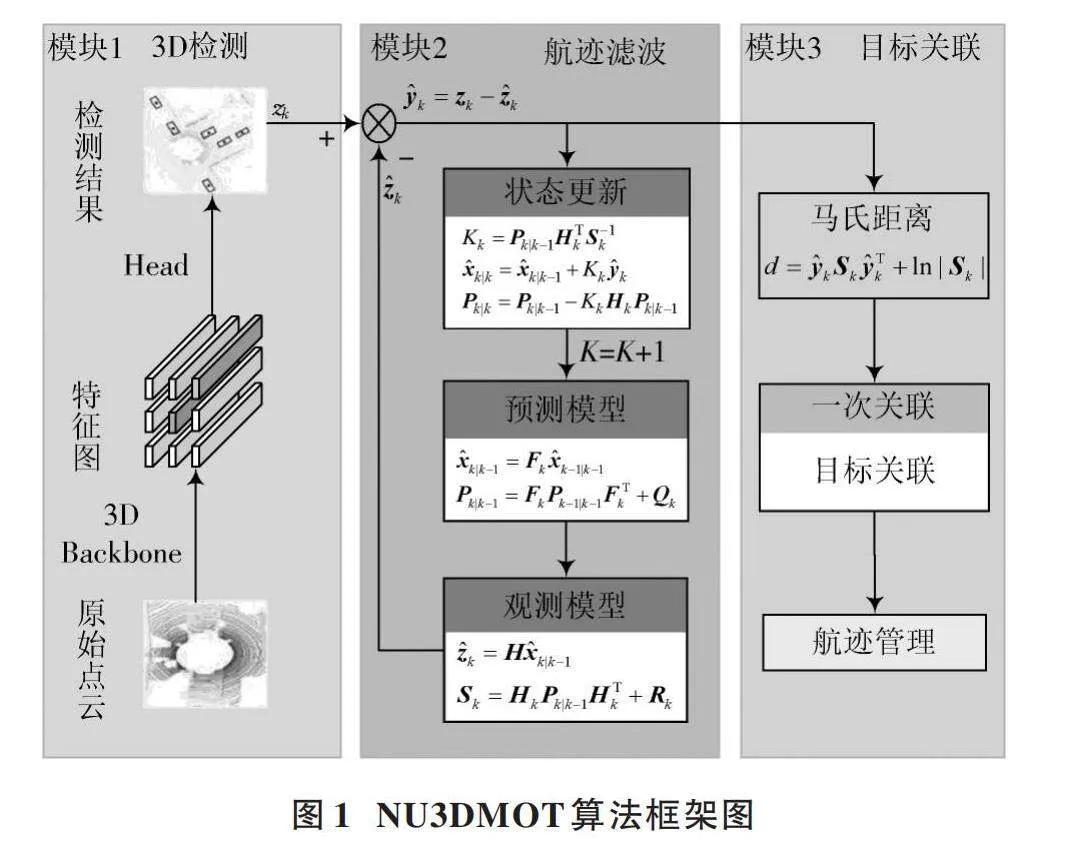
NU3DMOT算法整體框架如圖1所示。

1.1" 點云數據處理與目標檢測

近年來，出現了許多優秀的目標檢測算法，如Pointpillars[6]和PV?RCNN[7]。本文采用CenterPoint[8]作為目標檢測算法，其應用范圍廣，更便于本文算法與其他算法比較。目標檢測模塊如圖1中3D檢測模塊所示，原始點云經過3D骨干網絡（3D Backbone）處理得到特征圖，再經過2D?CNN架構的檢測頭得到BEV視角下的目標中心點，并根據中心特征回歸其他特征得到目標尺寸以及朝向。采用額外分支預測相鄰特征圖之間的目標位置偏移，獲取速度信息，最終將目標的信息表示成[zk=（px，vx，py，vy）]，并作為觀測值，其中參數依次為目標的x坐標、x方向的速度、y坐標以及y方向的速度。相比于其他利用卡爾曼濾波的多目標跟蹤算法，本文算法在觀測值中加入了速度信息，更加貼合目標的真實運動狀態，明顯提升了多目標跟蹤效果。

1.2" 航跡狀態預測

航跡狀態預測的關鍵是建立合適的運動模型。吳開陽等建立了一個恒定角速度模型[9]，但其狀態變量多達11維，大大增加了計算量，而本文僅使用4維向量[zk=（px，vx，py，vy）]表示狀態變量，其中[（px，py）]表示在BEV視角下的目標中心點坐標，[（vx，vy）]表示目標的分速度。整體模塊設計如圖1中的航跡濾波模塊所示，目標狀態在經過預測模型、觀測模型以及狀態更新后得到新一幀的后驗估計。

恒速模型卡爾曼濾波預測模型如式（1）所示。

[xk|k-1=Fkxk-1|k-1Pk|k-1=FkPk-1|k-1FTk+Qk] （1）

式中：[xk-1|k-1]表示k-1時刻目標狀態后驗估計；[xk|k-1]表示目標狀態在k時刻通過系統狀態轉移矩陣[Fk]預測的目標狀態先驗估計；[Pk-1|k-1]表示k-1時刻的預測協方差矩陣；[Pk|k-1]表示在k時刻預測步驟產生的預測協方差矩陣。假設過程噪聲即x、y軸方向的加速度滿足0均值高斯分布，[Qk]即為過程噪聲協方差矩陣。預測模型得到的先驗估計經過觀測模型處理得到后驗估計，觀測模型公式如式（2）所示。

[zk=Hxk|k-1Sk=HkPk|k-1HTk+Rk] （2）

式中：[H]為觀測矩陣；[xk|k-1]為先驗估計，兩者相乘可以將先驗估計轉換至觀測空間得到目標的預測測量值[zk]，以便在狀態更新步驟中與真實觀測值進行比較；[Sk]為新息協方差矩陣，其作用是估計殘差的不確定度大小；[Rk]為檢測誤差協方差矩陣。最后進行狀態更新步驟，得到卡爾曼濾波增益以及后驗估計等，狀態更新步驟如式（3）所示。

[yk=zk-zkKk=Pk|k-1HTkS-1kxk|k=xk|k-1+KkykPk|k=Pk|k-1-KkHkPk|k-1] （3）

式中：[yk]為觀測值[zk]與預測觀測值[zk]的殘差；[Kk]為卡爾曼濾波增益；[xk|k]為k時刻目標的后驗估計；[Pk|k]為k時刻的預測協方差矩陣。

1.3" 估計目標位置的不確定度

基于點云的目標檢測無需像基于相機的目標檢測一樣進行不同平面之間的坐標系轉換，檢測誤差相對較小，但由于點云的稀疏性以及測量目標距離傳感器的距離過遠，在檢測與跟蹤過程中依然存在誤差。大部分使用卡爾曼濾波算法進行預測的方法均采用固定的參數作為觀測噪聲協方差[Rk]中的值，并未考慮檢測目標物與檢測原點的距離遠近對測量造成的影響。針對此，NU3DMOT使用了一種自適應方法來計算目標位置的不確定度，并將其納入卡爾曼濾波的觀測噪聲協方差矩陣中，提高了跟蹤效果以及魯棒性。以距離為度量，認為離傳感器越遠的目標不確定性越大，首先根據自身位置以及測量目標計算歐氏距離，并歸一化以及平滑數據后進行平方操作，以此結果作為目標位置以及速度信息的不確定度系數，再經過計算得出位置以及速度信息對應的不確定度值。卡爾曼濾波中的觀測噪聲協方差矩陣[Rk]可以量化測量值的誤差或不確定性，將計算出的不確定度作為觀測向量[zk]中各個參數對應的[Rk]中的值，優化了卡爾曼濾波的觀測過程。

1.4" 數據關聯與匹配優化

k時刻的預測目標需要與k+1時刻的檢測目標關聯起來。本文選擇匈牙利匹配算法作為NU3DMOT的基礎數據關聯算法，其將多個元素之間的關聯問題轉化為最優的分配問題，并找到最佳的匹配方案。同時，針對不同置信度的目標，通過多次使用匈牙利算法分層次優化數據關聯過程，提升了關聯效率。在關聯度量的選取上，大部分算法如AB3DMOT[10]選取3D檢測框的交并比作為關聯度量，其計算量巨大且容易造成錯誤關聯；而NU3DMOT使用馬氏距離作為關聯度量，并考慮了不確定度的影響，更好地反映了樣本之間的關系。整體設計如圖1中目標關聯模塊所示，馬氏距離計算公式如式（4）所示。

[d=ykSkyTk+lnSk] （4）

式中：[yk]為測量殘差；[Sk]為測量協方差矩陣；[lnSk]為殘差協方差矩陣行列式的對數。這樣，確保了數據關聯決策不僅考慮測量和預測的差異，還考慮了測量的不確定性，將在對象跟蹤中產生可靠的關聯決策，同時，選取合適的生命周期管理航跡，使跟蹤算法魯棒性更強。

2" 實" 驗

為驗證上述跟蹤方法在實際復雜環境中的跟蹤性能，在公開數據集Nuscenes[11]上對算法進行評估，算法實現由C++編寫。

2.1" 離線實驗

2.1.1" Nuscenes數據集

本文使用Nuscenes跟蹤數據集。相比于只提供前視圖真值的KITTI數據集[10]，Nuscenes數據集提供環視真值注釋且道路情況更復雜，也更具挑戰性。本文在擁有150個場景且包含真值數據的驗證集以及擁有150個場景但不包含真值數據的測試集上，對提出的NU3DMOT算法進行驗證。

2.1.2" 評價指標

傳統的目標跟蹤評價指標，如多目標跟蹤精度（MOTA）、多目標跟蹤準確度（MOTP）[12]等沒有考慮低置信度目標對跟蹤過程帶來的不利影響。Weng X等人針對這一問題提出了新的評估指標且被Nuscenes數據集用于評估多目標跟蹤效果[13]。其中，最重要的指標是平均多目標跟蹤精度（AMTOA）以及平均多目標跟蹤準確度（AMTOP）。

2.1.3" 實驗結果

圖2為連續4幀的跟蹤效果展示圖。

圖中第1列為Nuscenes數據集采集車輛的前視攝像頭采集的道路圖像，第2列為車輛的激光雷達點云數據圖，圖的正中間為車頂搭載激光雷達傳感器的車輛，包絡框為CenterPoint算法檢測出的目標物體，字母D序列代表檢測目標id，字母T序列代表跟蹤目標id，通過“?”連接，代表檢測目標與跟蹤目標的關聯情況。由圖2可知，在前3幀中采集車輛前方較遠車目標被較近車目標遮擋，在第1幀、第2幀、第4幀中，盡管檢測器在不同幀賦予了車輛不同的檢測id，但這些檢測id依然可以與跟蹤器賦予的唯一跟蹤id正確關聯；而在第3幀中，由于較遠車輛受遮擋嚴重，檢測器并沒有給出有效的檢測id，但由于跟蹤器出色的魯棒性，依然通過預測為較遠車輛保留了跟蹤id，且在第4幀正確地將較遠車輛匹配至正確的軌跡。

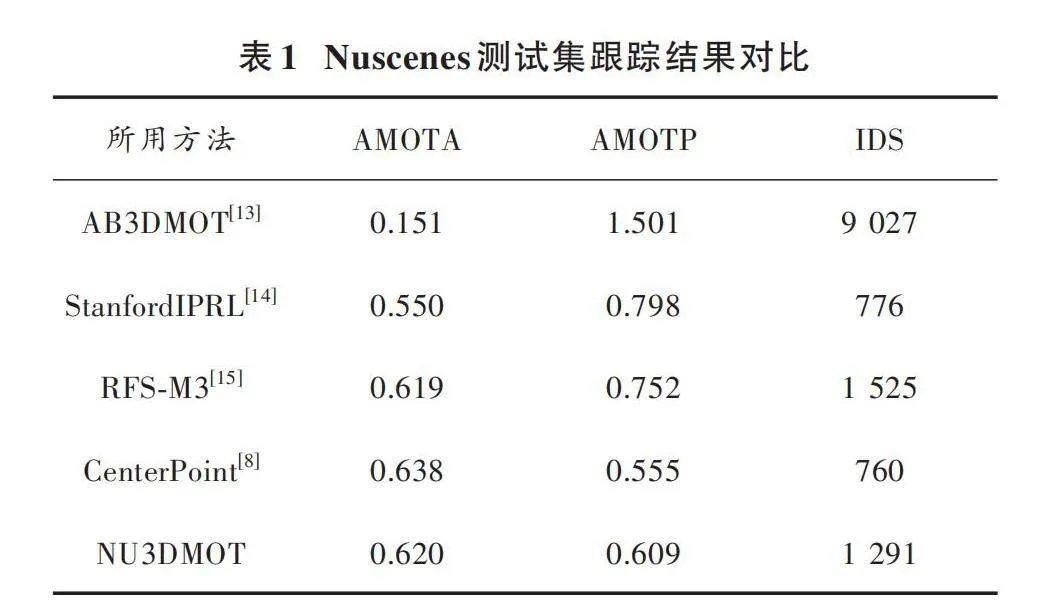
表1為常用的3D多目標跟蹤算法在Nuscenes測試集上的結果。

由表1結果可知，NU3DMOT的AMOTA指標比同樣使用卡爾曼濾波模型的Nuscenes數據集基線算法AB3DMOT高出46.9%。盡管AMOTA指標略低于CenterPoint算法，但NU3DMOT僅需要單個CPU運行速度即可達到1 000 f/s，而CenterPoint算法需要耗費大量算力且速度僅為16 f/s。NU3DMOT算法的AMOTP指標低于除CenterPoint外的其他幾種基于運動模型的算法，說明在建立運動模型的過程中加入目標的檢測包絡框參數并非是完全必要的，且這種做法會大大降低算法運行的速度，這也從側面反映了本文算法的簡潔性。NU3DMOT算法的IDS指標優于基線算法，但低于部分算法，其原因可能是恒速卡爾曼濾波模型對機動車轉向等情況并不靈敏。

2.2" 消融實驗

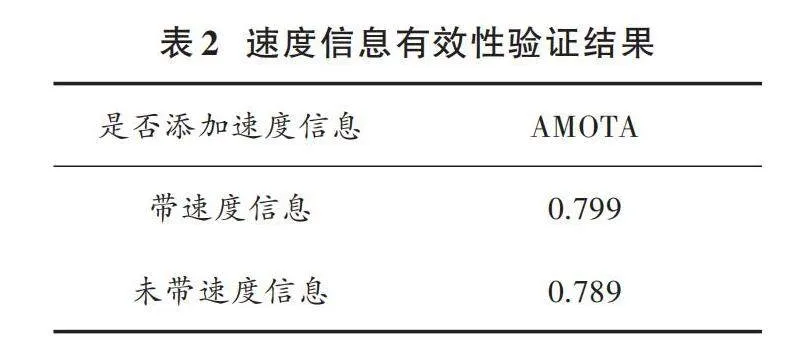
為了驗證觀測矩陣中添加速度信息給多目標跟蹤算法帶來的提升，在驗證集上對車類別進行實驗。評價指標為AMOTA，結果如表2所示。

由實驗結果可知，將速度信息添加至觀測矩陣時，AMOTA指標比未帶速度信息時高出1%。

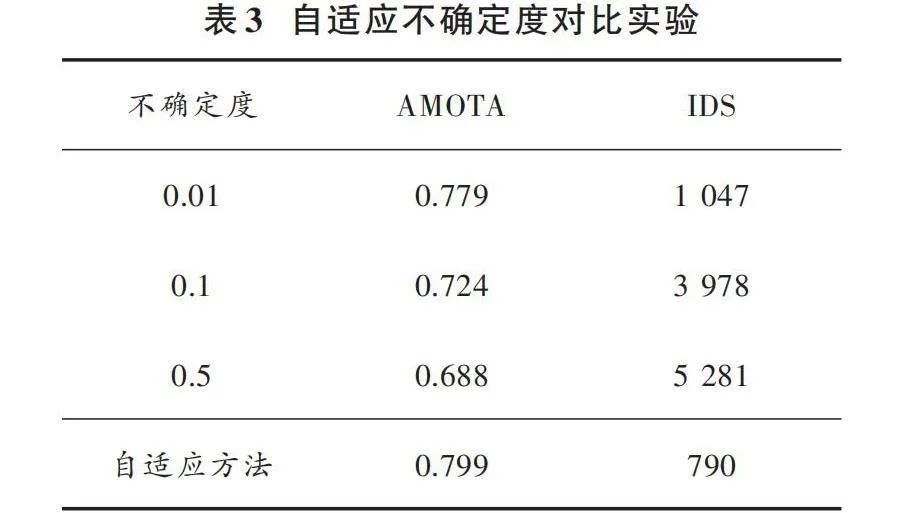
針對觀測模型中引入的目標自適應不確定度，在驗證集車類別上進行實驗，對比的評價指標為AMOTA以及IDS。實驗對比結果如表3所示。

由表3可知，自適應不確定度方法在跟蹤效果上要優于固定不確定度為常數時的跟蹤效果，能有效提高多目標跟蹤算法的魯棒性。

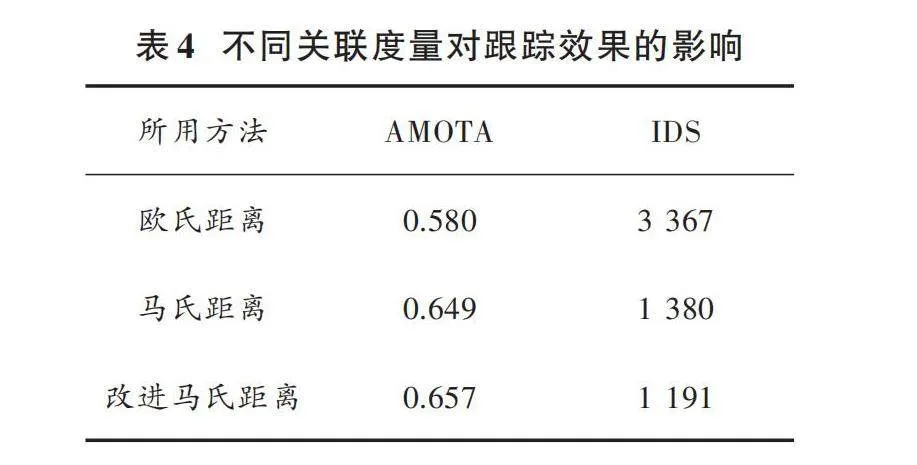
為了驗證結合不確定度的改進馬氏距離的有效性，本文在Nuscenes驗證集上利用歐氏距離、馬氏距離以及改進的馬氏距離對全類別目標進行實驗驗證，對比的評價指標為AMOTA以及IDS，結果如表4所示。

由表4可知，利用改進馬氏距離作為關聯閾值時，多目標跟蹤算法效果要優于另外兩種關聯閾值方法。其中AMOTA指標分別高出7.7%和0.8%，相較于其他方法，改進馬氏距離能更準確地關聯目標；同時，IDS指標也顯著低于另外兩種方法，這說明改進馬氏距離能夠提高多目標跟蹤系統的魯棒性。

3" 結" 論

本文針對復雜道路情況，提出了一個基于運動模型的NU3DMOT算法。首先，將速度信息納入觀測值中，對預測信息進行矯正，提升了多目標跟蹤效果；同時，利用位置信息考量不確定度以修正觀測模型中的測量協方差矩陣，優化卡爾曼濾波過程中對觀測信息的利用；然后，對馬氏距離做出改進，綜合考慮目標檢測不確定度的影響，并作為關聯度量；最后，利用匈牙利算法進行分層數據關聯。經過Nuscenes數據集的驗證集和測試集實驗證明，所提方法能夠有效提高多目標跟蹤效果，AMOTA比基線算法高出46.9%，有明顯優勢。

注：本文通訊作者為易可夫。

參考文獻

[1] 張弘，萬家旭，陳海波，等.BEVTrack：基于難例挖掘訓練的端到端三維多目標跟蹤方法[J].信號處理，2024，40（1）：152?165.

[2] 程鑫，周經美，劉霈源，等.基于任務聯合的三維車輛檢測與跟蹤集成算法[J].中國公路學報，2023，36（9）：288?301.

[3] 董艷秋，萬旺根，王旭智，等.基于中心點距離關聯的三維多目標跟蹤算法[J].工業控制計算機，2023，36（12）：12?14.

[4] 張華旭，劉崢，雷祖芳，等.基于改進數據關聯的三維多目標跟蹤算法[J].激光雜志，2024，45（1）：191?197.

[5] 陳伯云，陸安江，周驊，等.激光點云中三維多目標在線跟蹤方法[J].激光雜志，2023，44（4）：68?73.

[6] LANG A H， VORA S， CAESAR H， et al. Pointpillars： fast encoders for object detection from point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. [S.l.]： IEEE， 2019： 12697?12705.

[7] SHI S， GUO C， JIANG L， et al. PV?RCNN： point?voxel feature set abstraction for 3d object detection [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle， USA： IEEE， 2020： 10529?10538.

[8] YIN T， ZHOU X， KRAHENBUHL P. Center?based 3D object detection and tracking [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville， TN， USA： IEEE， 2021： 11784?11793.

[9] 吳開陽，秦文虎，云中華，等.基于激光雷達的三維多目標檢測與跟蹤[J].傳感器與微系統，2023，42（1）：122?125.

[10] GEIGER A， LENZ P， URTASUN R. Are we ready for autonomous driving？ The KITTI vision benchmark suite [C]// 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence， RI， USA： IEEE， 2012： 3354?3361.

[11] CAESAR H， BANKITI V， LANG A H， et al. Nuscenes： a multimodal dataset for autonomous driving [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle， USA： IEEE， 2020： 11621?11631.

[12] BERNARDIN K， ELBS A， STIEFELHAGEN R. Multiple object tracking performance metrics and evaluation in a smart room environment [EB/OL]. [2023?04?17]. https：//cvhci.anthropomatik.kit.edu/～stiefel/papers/ECCV2006WorkshopCameraReady.pdf.

[13] WENG X， WANG J， HELD D， et al. 3D multi?object tracking： a baseline and new evaluation metrics [C]// 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems （IROS）. Las Vegas， NV， USA： IEEE， 2020： 10359?10366.

[14] CHIU H， LI J， AMBRU? R， et al. Probabilistic 3D multi?modal， multi?object tracking for autonomous driving [C]// 2021 IEEE International Conference on Robotics and Automation （ICRA）. Xi’an： IEEE， 2021： 14227?14233.

[15] PANG S， MORRIS D， RADHA H. 3D multi?object tracking using random finite set?based multiple measurement models filtering （RFS?m3） for autonomous vehicles [C]// 2021 IEEE International Conference on Robotics and Automation （ICRA）. Xi’an： IEEE， 2021： 13701?13707.