變化中窺發展 比較中尋優化

［摘 要］ 基本不等式是高中數學的重要內容之一，對探尋最優方案解決實際問題大有裨益，能有效連接數學與現實生活. 采用比較研究法，詳細分析北師大版高中數學新舊教材中基本不等式的課標要求、知識編排、數學文化及例習題設置，利于新一輪教材編撰及教學策略優化. 基于研究結果提出三點教學建議：基于整體觀念調整“大單元”教學內容；以數學文化為“引”發揮真實效能；推進例習題設計多樣化.

［關鍵詞］ 高中數學教材；基本不等式；北師大版；比較研究

引言

教材的編寫與研究是教材建設工作相互聯系的兩個方面，前者為后者提供素材并展現其成果和水平，后者則為前者提供科學基礎昭示其改進方向［1］. 隨著《普通高中數學課程標準（2017年版2020年修訂）》的發布，新教材編撰再起波瀾. 因此，研究教材變遷，了解其發展與應用至關重要.

研究對比北京師范大學出版社于2011年和2019年出版的普通高中數學教科書（2011年出版的教科書簡稱舊教材，2019年出版的教科書簡稱新教材）中的基本不等式內容，原因有二：其一，基本不等式是高中數學聯系生活的重要橋梁，蘊含豐富的數學文化素材，涉及眾多數學思想方法. 隨著教育改革的推進，以及課程標準的更新換代，基本不等式相關內容更迭不斷，相較于基本不等式的教學、證明和應用研究，教科書方向的研究較少. 其二，國內數學教材比較研究多關注人教版，然其他版本教材亦有眾多可取之處. 北師大版是除人教版外使用范圍最廣的教材，曾獲國家教材委員會主辦、教育部承辦四年一次的“全國優秀教材（基礎教育類）”二等獎［2］. 研究擬從比較視角分析課標要求、知識編排、數學文化和例習題設置，明晰“基本不等式”內容在新舊教材變遷中的變化，以期以小見大，助力研究者掌握數學教材變革動向，并為新一輪教材編撰及一線教師合理使用教材提供參考借鑒.

研究內容與結果分析

1. 課標要求

課程標準是教材編寫和修訂的依據，因而剖析不同時期的課程標準利于明晰教材在改版過程中的編排脈絡與變革動向. 對比《普通高中數學課程標準（實驗）》（下文簡稱舊課標）與《普通高中數學課程標準（2017年版2020年修訂）》（下文簡稱新課標）對基本不等式的要求如表1所示.

從內容要求來看，新舊課標均對“內涵理解”與“公式應用”提出了要求. 就第一點而言，新課標對基本不等式行為動詞的要求從“探索并了解”提升為“掌握”，強調學習者需深入理解數學對象的本質特征. 而從第二點來看，新舊課標均強調學以致用，但新課標特別注重“結合具體實例”，強化理論與實踐的結合.

新舊課標均未對基本不等式作單獨提示，而是歸入“不等式”大類描述. 舊課標主要闡明不等式是刻畫區域的重要工具，而新課標則更注重數學思想方法的滲透，以及等式與不等式的共性與差異的探索.

從學業要求來看，舊課標未具體規定，新課標則重視核心素養目標，切合黨的教育方針，強調教材在立德樹人方面的價值.

2. 知識編排

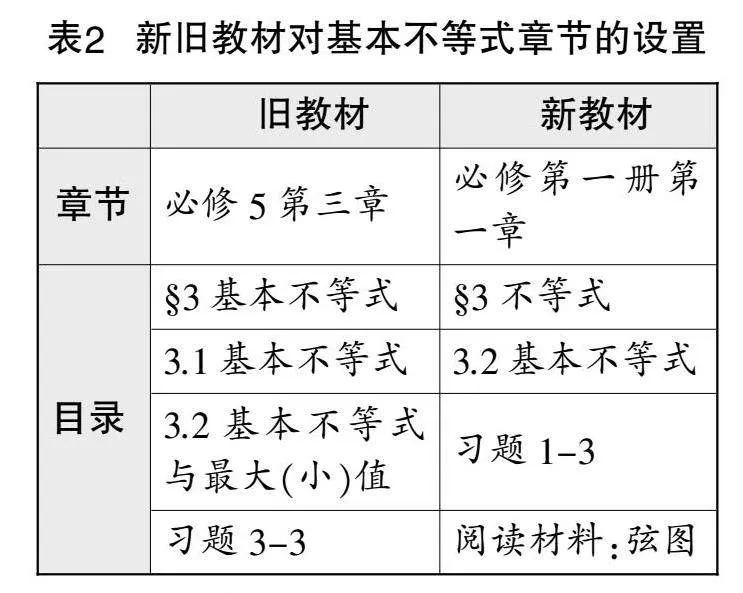
（1）章節設置

如表2所示，基本不等式在新舊教材中均屬必修內容，但舊教材中的基本不等式位于必修末尾（必修5），而新教材則將基本不等式移至必修第一冊第一章“預備知識”中，必修地位有所提升. 小學、初中初步學習了不等式，高中前置基本不等式，強化課程銜接，為后續學習函數最值奠定了基礎. 因此，教材修訂基本不等式章節，使學習順序更符合學生的認知發展水平.

（2）欄目設置

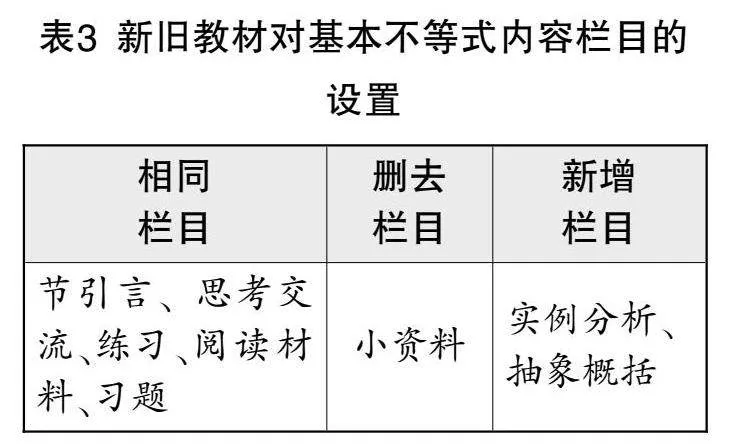
教材中的欄目是表征知識的一種方式，也是體現教材建構特色的一種形式，蘊含著豐富的教育教學價值［3］. 統計并比較新舊版教材的欄目設置，以明晰其編寫特色及異同（結果如表3所示）.

由表3可知，新舊教材均設置“思考交流”“閱讀材料”欄目，表明教材編寫注重學生拓展性思維的發展. 新教材將“小資料”欄目歸入同類的“閱讀材料”欄目，優化欄目編排設計. 同時，新教材在借鑒舊教材編排經驗的基礎上，新增了“實例分析”和“抽象概括”兩個欄目，強調學生自主探究和數學抽象素養的培養，促進學生通過實踐操作檢驗知識，加強數學與生活的聯系，提升學生分析和解決問題的能力.

3. 數學文化

（1）數學文化分類

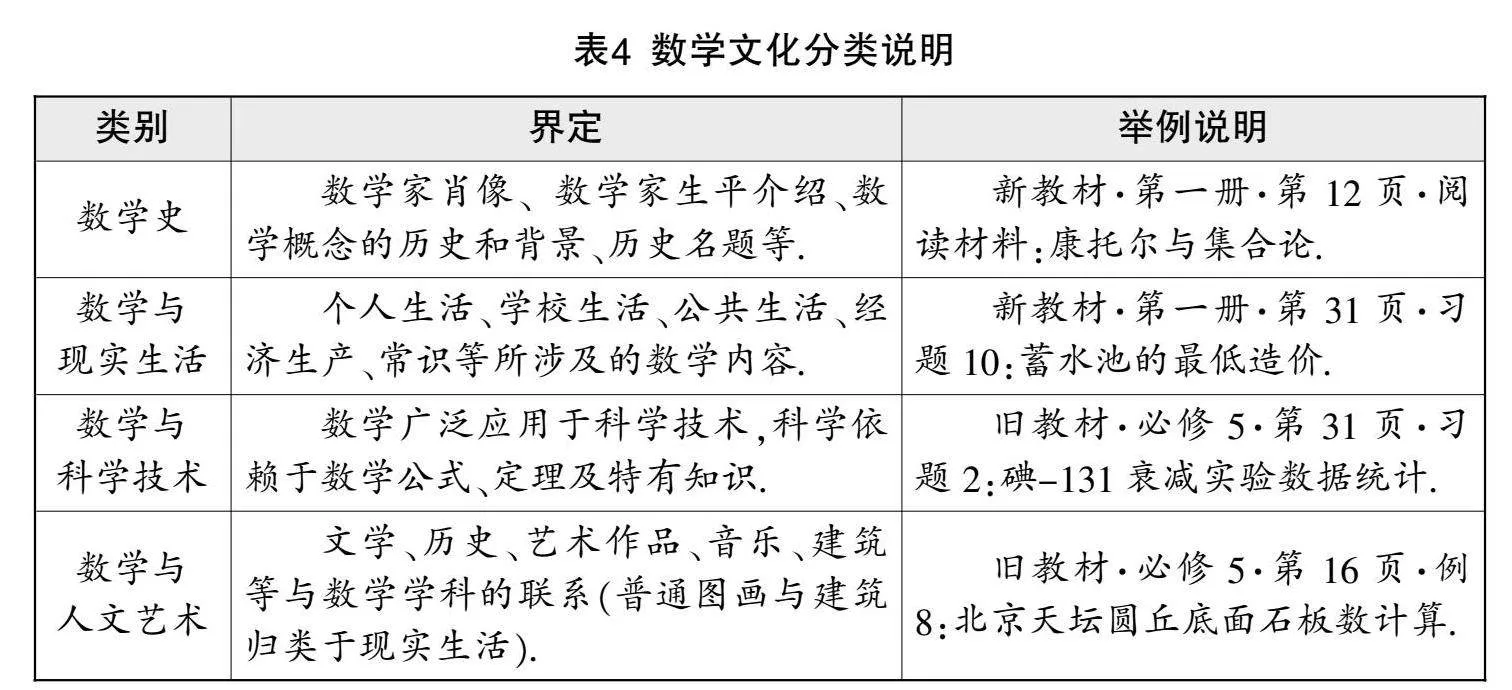
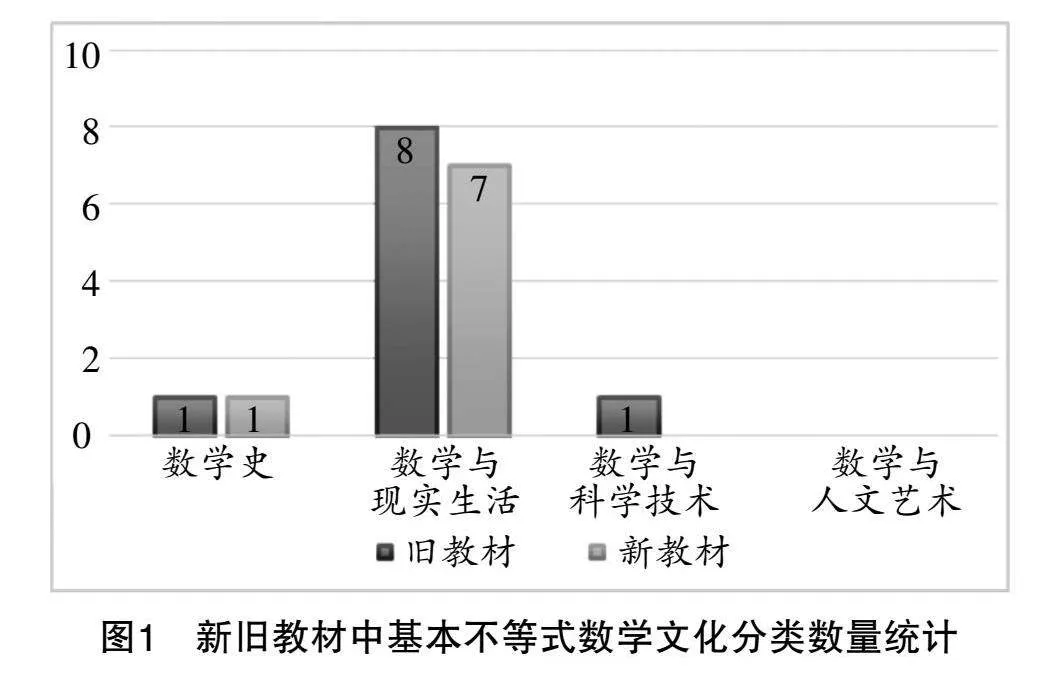
新舊課標均注重數學文化的滲透和價值體現［4］［5］. 借鑒王建磐和汪曉勤對數學文化的界定［6］，以新舊教材為例進行概括說明（見表4），并統計新舊教材中基本不等式數學文化的分類數量（見圖1）.

由圖1可知，兩版教材基本不等式數學文化以“數學與現實生活”為主，其他類別較少，且均未提及“數學與人文藝術”，分布不均. 新教材基本不等式內容總頁數（7頁）少于舊教材（10頁），說明其數學文化分布密度略大于舊教材.

（2）數學文化運用方式

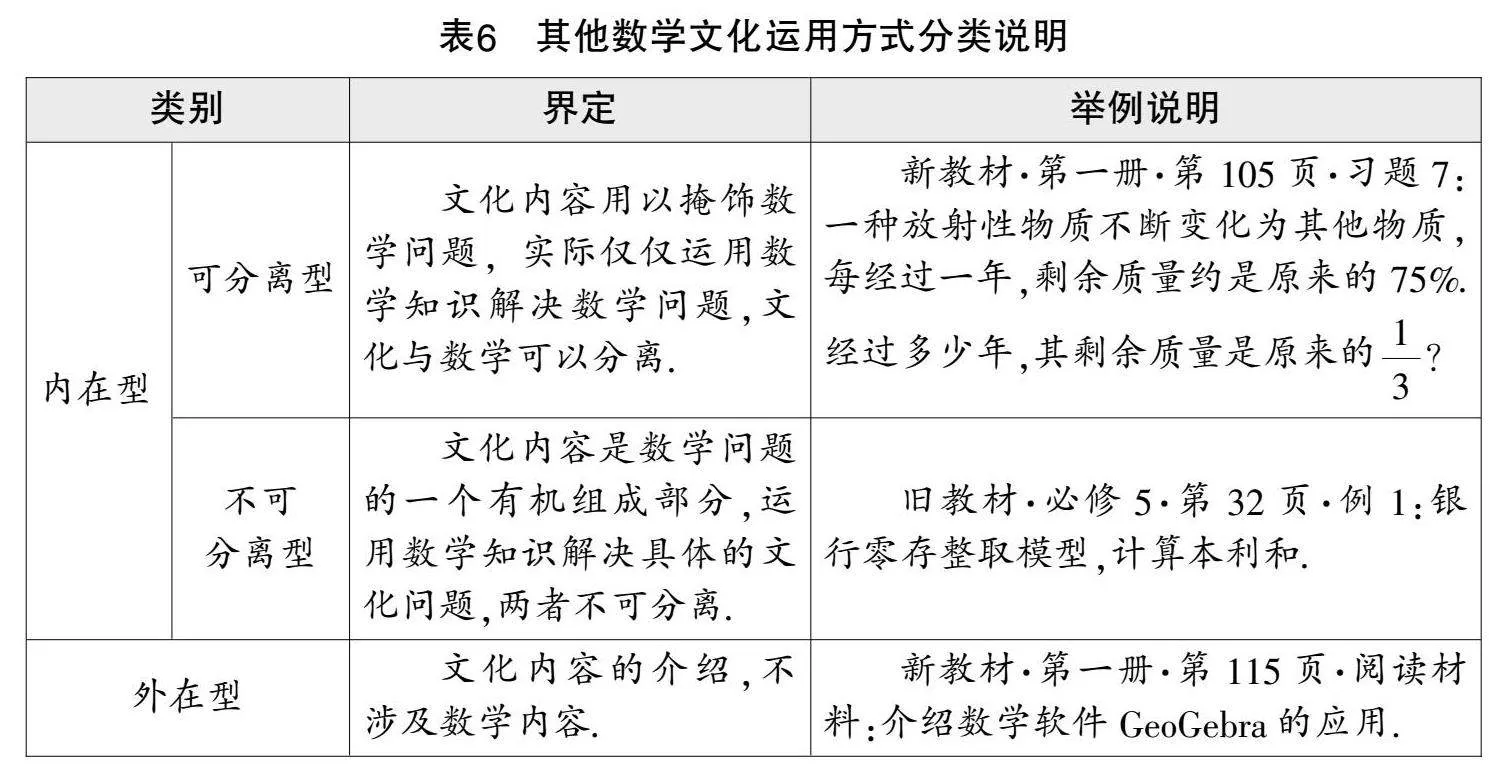
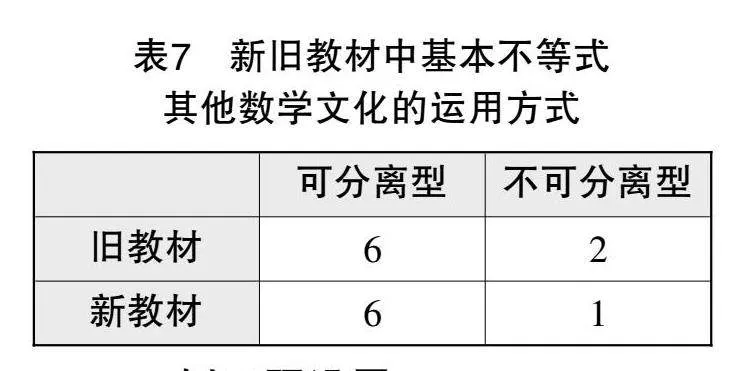
按數學文化與數學知識的關聯程度，數學史的運用方式分為五類：點綴式、附加式、復制式、順應式和重構式［7］（見表5）. 其他數學文化的運用方式可分為外在型和內在型（內在型又可細分為可分離型和不可分離型）［8］（見表6）.

如圖2、圖3所示，新舊教材均將趙爽弦圖史料置于節末，關聯國際數學家大會會標，讓史料有效鏈接現實. 其文字部分屬于重構式，與數學知識的關聯度較高；圖片部分屬于點綴式. 經統計，基本不等式內容中其他數學文化的運用方式大多屬于可分離型（見表7），與數學知識的關聯度較低，即去掉數學文化背景也不影響數學問題的解決.

4. 例習題設置

（1）例習題數量

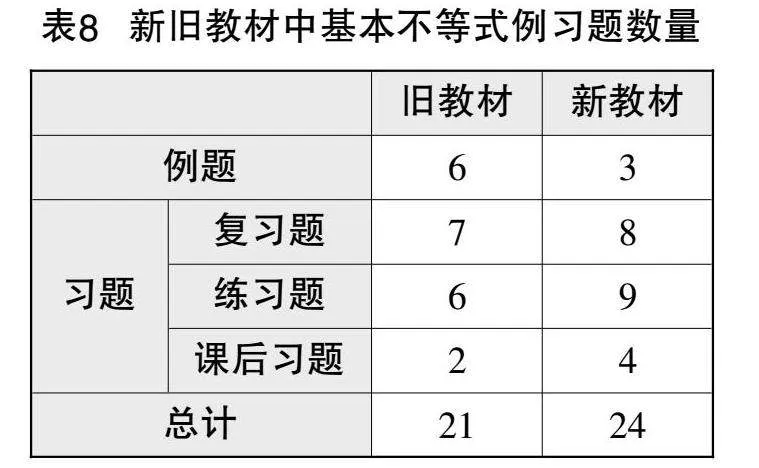
習題分為練習題（欄目標題帶有“練習”二字）、課后習題（欄目標題帶有“習題”二字）和復習題（通常出現于章末，涉及一章所有知識點）. 規定例習題的題量以小題數量為準：每一例習題出現一次計題量為1；若一大題包含4個小題且小題間無絕對關聯性，則計題量為4，否則為1；若一大題不包含任何小題，則計題量為1；若一小題存在多問，也計題量為1. 基于上述規定，對基本不等式相關例習題數量進行統計，如表8所示.

基本不等式在舊教材中共6道例題、15道習題，在新教材中共3道例題、21道習題. 通過比較可知，新教材中的例題減少了而習題增加了，更考驗學生的知識轉化與遷移能力. 此外，兩版教材的習題均設置為A組、B組，體現難度的分層設計，關注學生的差異性.

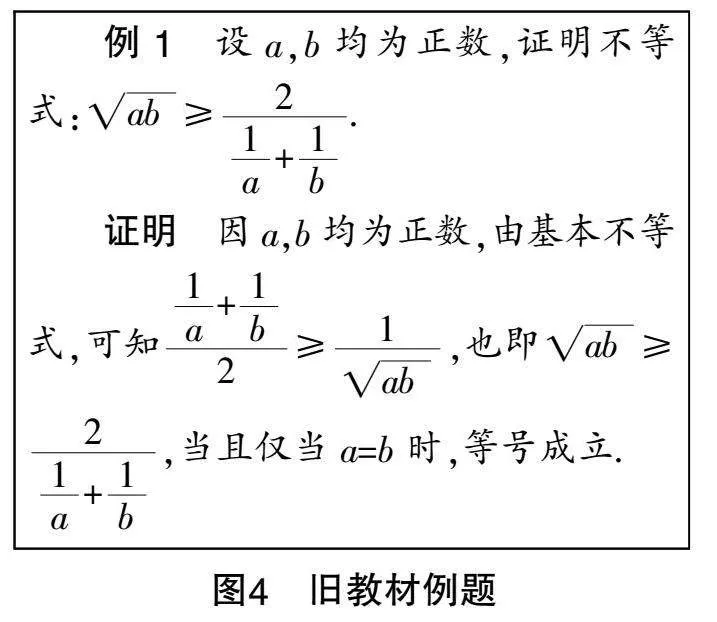
（2）例習題內容

新舊教材在例習題內容設置上也有所差異. 如圖4、圖5所示，舊教材將基本不等式相關知識點置于例題中，并給出證明過程；而新教材則將其置于習題中，不給證明過程，對學生的自主學習能力提出了更高的要求.

（3）例習題綜合難度

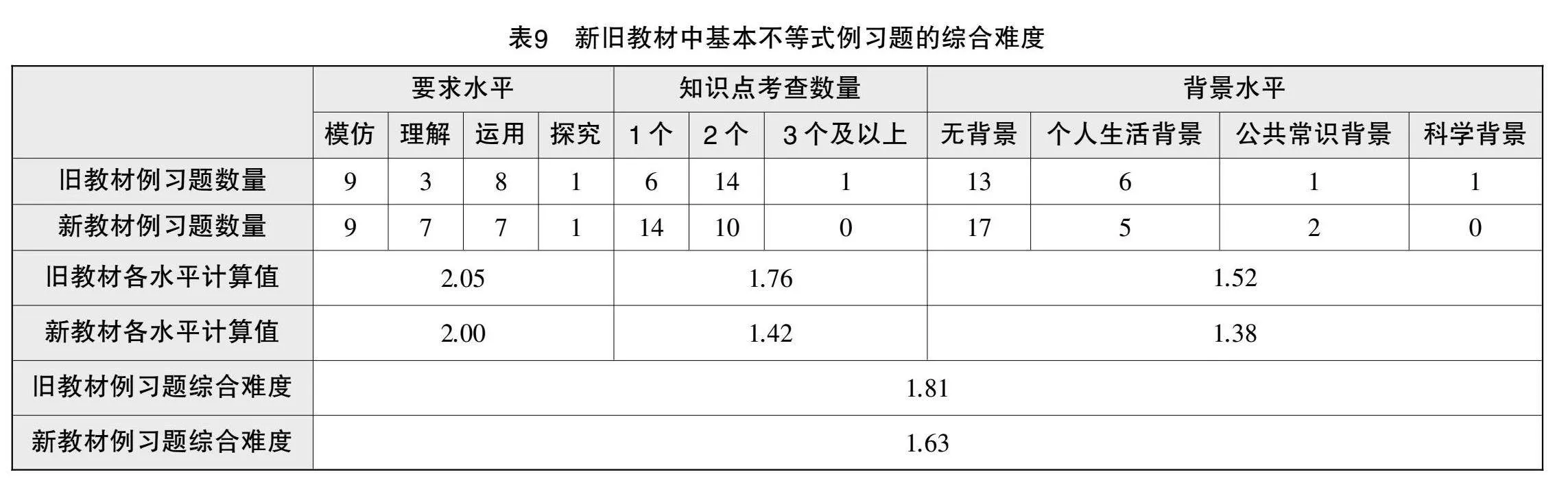
為深入了解基本不等式的例習題設置特征，借鑒吳立寶、王建波、曹一鳴［9］構建的難度分析框架，分別從要求水平（模仿、理解、運用、探究）、知識點數量（1個、2個、3個及以上）和背景水平（無背景、個人生活背景、公共常識背景、科學背景）三個維度進行統計，依據公式計算難度，結果保留兩位小數，如表9所示.

由表8、表9可知，雖然新教材中的例習題更多，但難度小于舊教材，表明教材沿革中，例習題對學生掌握知識程度的考查趨向基礎性. 就要求水平而言，新教材計算值小于舊教材，且兩版教材均較少設置探究類例習題；在知識點考查數量上，新教材計算值小于舊教材，且對1個知識點的考查居多，而舊教材主要考查2個及以上知識點；從背景水平來看，新教材計算值小于舊教材，兩者多設置無背景例習題（即純數學背景），表明教科書的編排始終重視數學知識本身，且有背景的例習題均以個人生活為主，科學背景較少. 總體而言，新教材在各個維度的計算值均小于舊教材，可見教材對例習題各維度的變遷趨向一致.

研究總結與建議

通過比較北師大版高中數學新舊教材基本不等式內容，洞察教材發展趨勢，提出三點建議，助力教師教學和教材編撰.

1. 基于整體觀念調整“大單元”教學內容

建構主義的學習觀強調應把學習者原有的知識經驗作為新知識的生長點，引導學習者從原有的知識經驗中，生長新的知識經驗［10］. 因此，對教育教學而言，知識過渡與銜接尤為重要. 新教材對基本不等式內容的調整可見一斑，其將基本不等式置于“預備知識”處，能有效銜接初中不等式與高中函數最值的學習.

基于此，教師教學時應立足課程標準，尊重學生的認知發展規律，在整體觀念下進行“大單元”教學設計. 基本不等式需要較高的抽象思維能力，而一元二次不等式與初中知識緊密相關. 為加強學生對數學思想方法的理解，建議將基本不等式教學置于一元二次不等式之后，以便學生更好地理解和應用新知識. 舊教材對這兩類專題的位置設計便是如此，教師可基于班級學情和自身教學能力進行考量.

2. 以數學文化為“引”發揮真實效能

近年來，學術界對數學文化的研究盛行，但需警惕誤區：將添加“星點”文化素材視為融入. 就基本不等式數學文化的比較結果而言，新舊教材對數學文化的分布不均，多為“數學與現實生活”類，可見兩版教材對數學文化素材的使用有限，且除史料用重構式呈現外，其他數學文化素材多屬可分離型，與數學知識的關聯程度較低，不利于發揮文化育人之效.

筆者通過訪談得知，教師和學生普遍擔憂“課前引入”會浪費課時，但直給式的知識遷移又顯枯燥乏味且不利于記憶，因而如何發揮引入實效成了亟待考量的難題. 事實上，除教材呈現的趙爽弦圖外，古今對基本不等式的探索、求解比比皆是. 如“歐拉羊圈”是等周面積最值問題的典型例子，作為探究性引入素材恰可銜接基本不等式，既有趣又易記，還重視知識發生和發展的過程. 現有數學文化素材可改編，如舊教材必修5以第24屆國際數學家大會會標（根據趙爽弦圖設計）為背景，設置探究題引入基本不等式，是優秀改編案例.

3. 促進例習題多樣化設計

例習題是數學教材的重要組成部分，有思維能力訓練、思想方法滲透、診斷反饋補救與育人等功能［11］. “一正、二定、三相等”是求解大多數基本不等式題的先決條件，而學生往往“知其然不知其所以然”. 建議增加改錯題，以豐富題型，由學生自主糾錯，強化知識點的學習，確保邏輯鏈完整.

窺一斑而知全豹，通過對例習題的多維度綜合比較，可知基本不等式各維度計算值及綜合難度均有所降低，說明教材重視基本不等式知識內容的基礎性，滿足課程標準的要求. 但隨著知識經濟時代的到來，時代性與發展性備受關注，因此例習題的多樣化設計應納入考量. 就北師大兩版高中數學教材關于基本不等式例習題而言，在要求水平上更多強調模仿與理解，較少設置探究類例習題，而探究恰是激發學生學習動力的有效途徑，故需在此加強例習題的多樣化設計. 值得注意的是，兩版教材例習題均缺背景，即使有背景，也多限于個人生活，公共常識與科學背景寥寥無幾. 基本不等式作為不等式學習的重要一環，不僅在數學上有廣泛應用，也深度融入物理、化學、地理等學科. 因此，問題情境的選擇應放眼至古今中外，從習題本身出發切實提升人文與應用價值，由此提高學生跨學科思維水平，真正達到例習題學以致用的效能. 需要注意的是，例習題的多樣化設計指向教育質量的提升，切不可舍本逐末.

參考文獻：

［1］ 曾天山.教材論［M］. 南昌：江西教育出版社，1997.

［2］ 中華人民共和國教育部.國家教材委員會關于首屆全國教材建設獎獎勵的決定［EB/OL］. （2021-10-9）［2022-12-1］. https：//www.moe.gov.cn/srcsite/A26/s8001/202110/t20211012_571686.html.

［3］ 張定強，梁會芳，楊怡. 數學學科核心素養導向的“三角函數”教材內容變革［J］. 數學通報，2021，60（12）：4-7.

［4］ 中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［M］. 北京：人民教育出版社，2020.

［5］ 中華人民共和國教育部.普通高中數學課程標準（實驗）［M］. 北京：人民教育出版社，2003.

［6］ 王建磐，汪曉勤，洪燕君. 中、法、美高中數學教科書中的數學文化比較研究［J］. 教育發展研究，2015，35（20）：28-32+55.

［7］ 汪曉勤. HPM：數學史與數學教育［M］. 北京：科學出版社，2017.

［8］ 沈春輝，柳笛，汪曉勤. 文化視角下“中新美法”四國高中數學教材中“簡單幾何體”的研究［J］. 數學教育學報，2013，22（4）：30-33+102.

［9］ 吳立寶，王建波，曹一鳴. 初中數學教科書習題國際比較研究［J］. 課程·教材·教法，2014，34（2）：112-117.

［10］ 萊斯利·P.斯特弗，杰里·蓋爾. 教育中的建構主義［M］. 高文，徐斌燕，程可拉，等，譯. 上海：華東師范大學出版社，2002.

［11］ 吳立寶，王富英. 數學教材習題“七功能”［J］. 教學與管理，2014（31）：66-68.