高中數學建模應立足生活

［摘 要］ 在生活基礎上數學建模，可幫助學生了解模型的形成與發展，為后續靈活應用模型解決實際問題奠定基礎. 文章以“指數函數的概念”教學為例，借助兩個旅游景區不同年份游客人次的變化情況，引導學生親歷“初建模型—求解模型—應用模型—總結提升”等環節，培養學生的數學思維，提升學生的建模能力，為發展學生的數學學科核心素養夯實基礎.

［關鍵詞］ 數學建模；知識；生活；指數函數

數學建模素養是《普通高中數學課程標準（2017年版2020年修訂）》提出的六大數學學科核心素養之一. 數學模型對學生來講并非一件新鮮事物，作為核心素養，其在不同階段的表現是不同的，從小學階段的模型意識到初中階段的模型觀念再到高中階段的數學建模，經過了一個螺旋上升的發展過程.

數學本身是非凡、多樣、多彩的. 隨著新課改的深入推進，數學教師應達成這一共識：不同個體學習數學的方式有所區別，學習數學知識的目的是更好地解決生活問題，數學課堂教學應想辦法激活各個層次學生的思維，挖掘學生的潛能，讓學生將數學知識與生活實際有機地融合起來，為發展數學學科核心素養創造條件. 在課堂中強化建模實踐，不僅能拉近生活實際與數學知識的距離，還能給學生帶來豐富的學習體驗，讓學生領悟數學知識到生活實際的可行之道［1］.

教學過程

1. 導入新課，初建模型

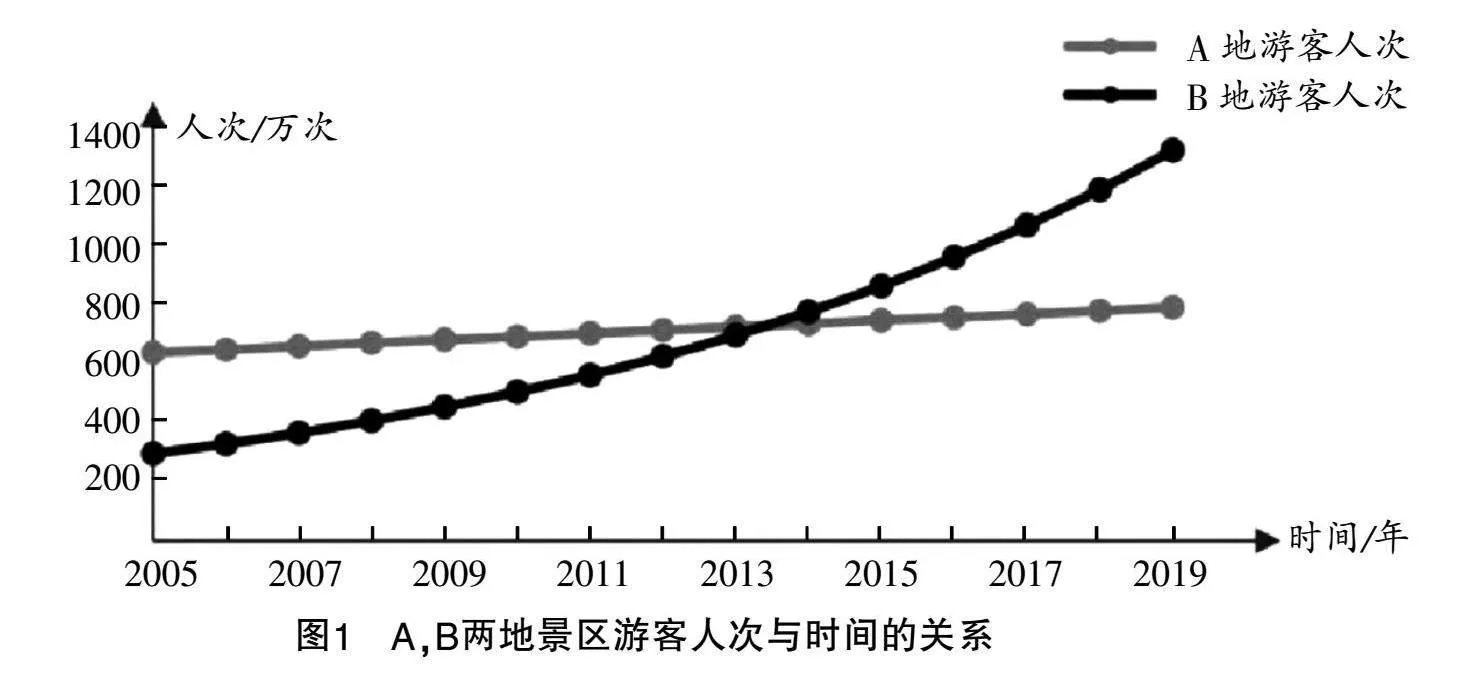
師：隨著我國經濟高速增長，人民生活水平不斷提高，不少家庭每年都會以旅游的方式增長見識，愉悅身心，各景區游客量日益遞增. 如表1所示，此為A，B兩地景區2005年至2019年游客人次的變化情況. 通過對表格的觀察，可發現什么規律？如何用數學知識來研究并描述這一現象？

在該生活情境的啟發下，學生借助描點法將表格中的數據整理為散點圖，并將各個點用光滑的曲線連接起來構成圖1. 觀察圖形，可見A地景區的游客人次近似于直線上升，即線性增長；B地景區的游客人次則是非線性增長，各點連接而成的曲線沒有明顯的變化規律.

設計意圖 將學生感興趣的生活實際作為教學情境，意在引導學生感知建模過程中的理解問題與簡化問題兩個環節. 從理解問題的視角來看，學生從A，B兩地景區游客人次的變化情況中可抽象出相應的數學問題，初步感知生活實際與數學知識的聯系；從簡化問題的視角來看，將表格數據簡化為散點圖，學生可直觀洞察游客人次的變化情況，抽象出現實模型，增強數據分析能力.

2. 生成概念，求解模型

（1）大膽猜想

師：B地景區的游客人次變化情況可借助什么量來表達？

探索此問題，可進入師生活動階段：教師先帶領學生將A地景區的游客人次與時間的函數表達式（y=10x+600，x∈［0，14］，x∈N），以及當年游客人次與次年游客人次的關系（yn+1-yn=10〈等差〉，n∈N）抽象出來，再要求學生獨立思考與合作交流，對B地景區各年的游客人次變化情況加以探索，猜想模型.

學生在交流過程中逐一排除一次函數、正比例函數、反比例函數，有的學生提出B地景區的游客人次的變化規律與二次函數相似，那么，這是否正確科學呢？為了探索這個問題，學生自主列式（y=ax2+bx+c，yn+1-yn=a+2an+b），同時畫圖分析，發現這組數據的變化規律與二次函數也不相符.

設計意圖 大膽猜想，可縮小模型范圍，為學生思維明確方向，也為學生從生活中提取數學模型，以及后續求解數學模型夯實基礎.

（2）構建模型

師：相鄰兩年間的游客人次相減獲得A地景區游客人次的年增長量，對于B地景區的游客人次的變化規律，能否用同種方法來分析呢？是否有其他方法？B地景區每年的游客人次增長量存在怎樣的情況？

在教師指導下，學生根據2006年至2018年B地景區游客人次的變化情況建立新模型，并用新模型計算2019年B地景區的游客人次，將所得結果與已知數據進行類比，判斷所構建的新模型是否準確科學.

探索發現年增長率和年增加量是該生活情境中的兩個重要變化量，而B地景區無法與A地景區一樣借助年增加量獲得游客人次的變化規律，由此考慮用年增長率來探索B地景區當年的游客人次與上一年的游客人次的關系，即通過相除得到=a，=a，…，=a，獲得模型=ax-1.

設計意圖 通過數據與圖象分析，學生自主進入建模狀態，并在大膽猜想與思考的基礎上，建構適合情境的新模型. 在此過程中，學生主動參與建模活動，感知建模步驟，體會數學知識、生活實際與建模之間的聯系，建立學習自信，發展數學思維.

（3）求解模型

學生通過獨立思考、自主計算與探索、合作交流，發現B地景區每年的游客人次增長率穩定在一個常數附近. 根據這個特點猜想B地景區游客人次的變化規律為=1.11x-1（x∈［1，+∞）. 至此，學生的思路變得明確.

設計意圖 學生基于運算、總結與探索，提升數學運算素養與思維水平，為構建數學模型奠定基礎.

3. 深化理解，完善模型

要求學生解釋怎樣根據數據獲得相應模型，并且探索所獲得的模型與現實生活是否相符.

在教師啟迪下，學生以小組合作交流的方式進行思考與分析，獲得如下結論：從2006年起，B地景區每年的游客人次為2005年游客人次的1.11， 1.112，1.113，…，1.11x倍. 設經過x年后B地景區的游客人次為2005年游客人次的y倍，則y=1.11x（x∈［0，+∞））. 根據模型y=1.11x（x∈［0，+∞））計算2019年B地景區的游客人次是278×1.1115-1≈1198（萬次），與2019年B地景區的實際游客人次1244（萬次）相比，誤差為3.7%. 實踐表明，模型數據與實際數據誤差較小，因此確定該模型具有可靠性，可用于解決實際問題.

設計意圖 此環節涉及建模過程中的“結果解釋”與“修改模型”兩個步驟. 基于結果解釋的維度思考，即使能自主建立模型，并不表示學生已經完成了教學任務，親歷建模過程，能將模型的來龍去脈描述得清清楚楚才算是真正意義上理解了模型. 修改模型是指在實際應用模型前，檢驗模型與生活實際的匹配程度. 應用數形結合思想探索模型，讓學生體驗實際數據與模型數據的誤差，認識到數學的周密性、嚴謹性和規范性，培養邏輯思維能力.

4. 拓展應用，發散思維

師：當生物死亡后，它機體內原有的碳14含量會按確定的比率衰減，大約每經過5730年衰減為原來的一半. 按照這種衰減規律，生物體內碳14含量與死亡年數之間有怎樣的關系？

因為有了景區游客人次探索的基礎，所以大部分學生都能通過獨立思考構建出模型y=

（x∈［0，+∞））.

師生共同總結兩函數的共性，發現函數y=1.11x和y=

都可以表示為y=ax（a>0，a≠1），其中x是自變量. 學生親歷建模過程，不僅自主獲得了可以解決生活實際問題的模型，還自然而然地理解了指數函數.

設計意圖 拓展教學內容，讓學生自主體驗一個完整的建模過程，此為深化與鞏固學生理解建模流程的過程，也是增進數學知識與生活實際聯系的過程. 學生在建模中體驗、思考與感悟，獲得“四基”與“四能”的同時，發展良好的數學建模素養.

5. 應用模型，凝練提升

問題1 如果平均每位游客出游一次可給當地帶來1000元門票之外的收入，A地景區的門票價格為150元，B地景區沒有門票，那么A，B兩地景區在2005年至2019年之間，由游客帶來的收入有多少？

問題2 某種生物死亡1萬年后，其體內碳14的含量會衰減為原來的百分之幾？

設計意圖 知識到生活的關鍵在于靈活應用所學知識解決實際問題. 本節課的教學重點是引導學生感知建模過程，發展學生的建模素養，能讓學生應用所構建的模型解決實際問題. 引導學生應用指數函數模型來分析上述兩個問題，一方面可進一步深化學生對指數函數概念的理解，另一方面可增強學生的知識應用能力，發展學生的數學學科核心素養.

6. 回顧總結，發展學力

課堂尾聲，要求學生自主總結建模基本步驟，感受建模思想. 鼓勵學生自評、互評課堂中的表現，提升反思與總結能力.

設計意圖 回顧學習過程，促使學生自我反省，為構建完整的知識結構奠定基礎，也讓學生將所學知識與技能轉化為內在素養和能力.

教學思考

結合本節課教學來看，數學建模離不開生活實際的支撐，遵循“生活—知識—生活”的流程. 在教學實踐中，教師要充分了解學情，以學生認知范圍內的實際問題為教學起點，通過問題驅動建模教學，并將提問的權利還給學生，從真正意義上激發學生的潛能，發展學生的數學思維和數學學科核心素養.

值得注意的是，從知識到生活的高中數學建模實踐在發現并提出問題、建立模型、求解模型與完善模型等環節，一定要基于深度學習的角度出發，時刻遵循“以生為本”教學理念，避免流于形式，此為發展學生數學學科核心素養的重要舉措.

總之，數學建模源于生活，服務于生活，其內容和理念應根植于生活之中［2］. 建立在學生已有認知基礎上，根據學生的生活經驗構建數學模型，不僅能體現生活的“數學味”，還能凸顯數學知識的“生活味”，揭露知識與生活的關聯性. 從知識到生活的建模實踐，需教師反復探索與打磨，設計出科學的情境問題，提升學生的創新意識，發展學生的建模素養.

參考文獻：

［1］ 周學君，龔雨欣，董清艷. 指向數學建模素養的高中數學教學設計框架及實施：以人教A版“指數函數的概念”為例［J］. 黃岡師范學院學報，2023（12）：80-85.

［2］ 周穎. 從知識到生活的高中數學建模實踐研究［J］. 數學教學通訊，2023（18）：52-53+60.