基于K-prototypes的混合屬性數(shù)據(jù)聚類(lèi)算法改進(jìn)

摘 要：屬性數(shù)據(jù)分為數(shù)值型數(shù)據(jù)和分類(lèi)型數(shù)據(jù)，一般情況下對(duì)于數(shù)值型數(shù)據(jù)運(yùn)算前要進(jìn)行標(biāo)準(zhǔn)化處理，但是對(duì)于數(shù)值型數(shù)據(jù)差異大的數(shù)據(jù)，由于大數(shù)掩蓋小數(shù)的影響，按照K-prototypes聚類(lèi)算法，數(shù)值型數(shù)據(jù)標(biāo)準(zhǔn)化后而且不對(duì)相應(yīng)的分類(lèi)數(shù)據(jù)有任何預(yù)處理或者在計(jì)算時(shí)沒(méi)有進(jìn)行任何改變，很可能提高分類(lèi)數(shù)據(jù)在聚類(lèi)中的影響，并且分類(lèi)型數(shù)據(jù)并未進(jìn)一步地細(xì)分，不能滿足不同要求的混合屬性聚類(lèi)。該文在將數(shù)值型數(shù)據(jù)標(biāo)準(zhǔn)化的基礎(chǔ)上，將分類(lèi)數(shù)據(jù)細(xì)分為二元數(shù)據(jù)和類(lèi)型數(shù)據(jù)，并用相異度系數(shù)距離計(jì)算分類(lèi)數(shù)據(jù)之間的距離，并且賦予二元和類(lèi)型數(shù)據(jù)相應(yīng)的權(quán)重，來(lái)改進(jìn)K-prototypes聚類(lèi)算法，使該算法滿足不同要求的混合屬性數(shù)據(jù)聚類(lèi)，最后通過(guò)C#語(yǔ)言，在ArcEngine2010版本上實(shí)現(xiàn)。

關(guān)鍵詞：K-prototypes算法；混合屬性；類(lèi)型數(shù)據(jù)；相異度系數(shù)；加權(quán)屬性

中圖分類(lèi)號(hào)：TP311.1 文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：2095-2945（2024）28-0031-05

Abstract： Attribute data is divided into numerical data and classification data. Generally， numerical data needs to be standardized before operation. However， for data with large differences in numerical data， since the large number hides the influence of decimal numbers， according to the K-prototypes clustering algorithm， after the numerical data is standardized and the waterlogging classification data is not preprocessed or changed during calculation， the influence of classification data in clustering is likely to be improved. Moreover， the classified data has not been further subdivided and cannot meet the different requirements of mixed attribute clustering. Based on standardizing numerical data， this paper divides classified data into binary data and type data， uses dissimilarity coefficient distance to calculate the distance between classified data， and assigns waterlogging weights to the binary and type data to improve the K-prototypes clustering algorithm， so that the algorithm can meet different requirements for mixed attribute data clustering. Finally， it is implemented on ArcEngine2010 version through C# language.

Keywords： K-prototypes algorithm; mixed attributes; type data; dissimilarity coefficient; weighted attributes

聚類(lèi)分析是人類(lèi)認(rèn)識(shí)客觀事物最樸素、最常用的手段之一，也是人類(lèi)認(rèn)識(shí)自然最基本、最有效的技能之一[1]。從簡(jiǎn)單的“物以類(lèi)聚，人以群分”到用數(shù)學(xué)工具去提取相關(guān)聯(lián)的信息，聚類(lèi)分析快速發(fā)展成為重要的數(shù)據(jù)挖掘技術(shù)，有效地改變了現(xiàn)代“數(shù)據(jù)豐富，信息貧乏”的困境[2-3]。

MacQueen于1967年首次提出了K-means聚類(lèi)算法[4]，但是此算法只能對(duì)數(shù)值屬性進(jìn)行處理，對(duì)其他的分類(lèi)數(shù)據(jù)無(wú)法處理。1998年，Huang[5]提出了K-modes算法，此算法雖然能夠通過(guò)匹配差異描述相異性對(duì)分類(lèi)屬性數(shù)據(jù)進(jìn)行處理，但對(duì)于混合屬性數(shù)據(jù)的處理還是存在一定不足。Huang等[6]進(jìn)一步將K-modes算法在K-prototypes算法中推廣應(yīng)用，用以解決分類(lèi)屬性數(shù)據(jù)和混合屬性數(shù)據(jù)的聚類(lèi)問(wèn)題。

隨后又有很多基于K-prototypes算法的改進(jìn)算法，如2007年趙立江等[7]改進(jìn)混合屬性聚類(lèi)算法，2010年陳丹等[8]研究一種改進(jìn)的混合屬性聚類(lèi)算法的初始中心點(diǎn)選擇算法，2010年陳韡等[9]基于K-prototypes混合屬性數(shù)據(jù)聚類(lèi)算法的分類(lèi)屬性相異度，以及2013年白天等[10]的混合屬性聚類(lèi)新方法從全局上把握初始原型，還有2014年劉強(qiáng)等[11]改進(jìn)的加權(quán)K-prototypes算法等，都是從初始點(diǎn)選擇或者聚類(lèi)原型選擇以及分類(lèi)屬性相異度計(jì)算的基礎(chǔ)上進(jìn)行算法的改進(jìn)，并未進(jìn)一步對(duì)分類(lèi)數(shù)據(jù)劃分計(jì)算。為此，本文在將數(shù)值型數(shù)據(jù)標(biāo)準(zhǔn)化的基礎(chǔ)上，將分類(lèi)數(shù)據(jù)細(xì)分為二元數(shù)據(jù)和類(lèi)型數(shù)據(jù)，并用相異度系數(shù)計(jì)算分類(lèi)數(shù)據(jù)之間的距離，并且賦予二元和類(lèi)型數(shù)據(jù)相應(yīng)的權(quán)重，進(jìn)一步改進(jìn)K-prototypes聚類(lèi)算法，使該算法滿足不同要求的混合屬性數(shù)據(jù)聚類(lèi)，最后通過(guò)C#語(yǔ)言，在ArcEngine2010版本上實(shí)現(xiàn)。

1 K-prototypes算法

把K-means及K-modes兩種算法相融合，引入?yún)?shù)γ，在聚類(lèi)過(guò)程中能夠?qū)崿F(xiàn)對(duì)數(shù)值屬性以及分類(lèi)屬性的權(quán)重的控制[3]。令X={X1，X2，X3，…，Xn}表示具有n個(gè)樣本的數(shù)據(jù)集，其中Xi=[Xi1，Xi2，…，Xip，Xi（p+1），…，Xim]表示第i個(gè)樣本的m個(gè)屬性值（1至p表示數(shù)值型數(shù)據(jù)屬性，p+1至m表示分類(lèi)型數(shù)據(jù)屬性）。使數(shù)據(jù)集的初始聚類(lèi)數(shù)為k，V={V1，V2，…，Vk}為對(duì)應(yīng)模的集合，聚類(lèi)過(guò)程中迭代聚類(lèi)集為C={C1，C2，…，Ck}，Ci=[Ci1，Ci2，…，Cik]：①首先確定類(lèi)的個(gè)數(shù)k，并為每個(gè)類(lèi)選擇k個(gè)初始的聚類(lèi)原型；②對(duì)樣本與各原型的距離進(jìn)行計(jì)算，根據(jù)計(jì)算結(jié)果，把樣本劃分到距離最近的聚類(lèi)原型相應(yīng)的聚類(lèi)中；③重新計(jì)算各個(gè)聚類(lèi)相應(yīng)的聚類(lèi)原型；④循環(huán)③及④，至每個(gè)聚類(lèi)中數(shù)據(jù)對(duì)象趨于穩(wěn)定，迭代F（X，V）無(wú)變化，方可停止。

定義1[5]數(shù)值屬性的距離測(cè)量采用歐幾里得距離的平方，樣本Xi與模Vl數(shù)值屬性的距離定義為

d1（Xi，Vl）=∑Xij-Vlj。 （1）

采用海明威距離公式進(jìn)行類(lèi)屬性距離計(jì)算，樣本Xi以及模Vl類(lèi)屬性的距離為d2（Xi，Vl）

d2（Xi，Vl）=∑δ（Xij，Vlj）， （2）

式中：當(dāng)Xij=Vlj時(shí)，δ（Xij，Vlj）=1；當(dāng)Xij≠Vlj時(shí)δ（Xij，Vlj）=0。

定義2[5]相異性測(cè)量函數(shù)計(jì)算樣本到模的距離，d（Xi，Vl）為樣本Xi至模Vl的距離

d（Xi，Vl）=∑Xij－Vlj+γ∑δ（Xij，Vlj）

=d1（Xi，Vl）+γd2（Xi，Vl）

式中：γ表示分類(lèi)屬性的權(quán)重值；δ表示分類(lèi)屬性的相異度。

定義3[9]求解聚類(lèi)優(yōu)化問(wèn)題的目標(biāo)函數(shù)（代價(jià)函數(shù)）

F（X，V）=∑∑uijd（Xi，Vj） ， （4）

∑uij=1；uij∈[0，1] ， （5）

式中：uij為1時(shí)，表示樣本Xi在類(lèi)Cl中；uij為0，則不屬于類(lèi)Cl。

1.1 屬性數(shù)據(jù)類(lèi)型

屬性數(shù)據(jù)類(lèi)型一般可以分為數(shù)值型屬性數(shù)據(jù)和分類(lèi)型屬性數(shù)據(jù)，同時(shí)分類(lèi)屬性數(shù)據(jù)中又包括值均為0和1類(lèi)型的數(shù)據(jù)以及其他類(lèi)型的數(shù)據(jù)，由于二元數(shù)據(jù)值只有0和1，任意2個(gè)維度的相同屬性值相等的概率一般比較大，所以即使二元屬性所賦權(quán)重值較小也有很高的相似性，而其他的類(lèi)型數(shù)據(jù)同屬性相比相等的概率就比較低，所以要相當(dāng)?shù)臋?quán)重值才能保證一定的相似性。因此，根據(jù)不同專(zhuān)題屬性的要求和影響以及分類(lèi)可操控程度的不同，將分類(lèi)型數(shù)據(jù)分為二元屬性數(shù)據(jù)和類(lèi)型屬性數(shù)據(jù)。

數(shù)值型數(shù)據(jù)比較常見(jiàn)，也是聚類(lèi)的基礎(chǔ)數(shù)據(jù)類(lèi)型。對(duì)于二元屬性數(shù)據(jù)通常取值只有0和1兩個(gè)狀態(tài)，此類(lèi)屬性相似性度量聚類(lèi)方面通常采用匹配測(cè)度，比如農(nóng)業(yè)數(shù)據(jù)中種植作物的有和無(wú)等均可用1和0二元數(shù)據(jù)表示。而類(lèi)型數(shù)據(jù)通常為0，1，2，…，n等整數(shù)，分別代表不同數(shù)據(jù)的不同類(lèi)別，比如農(nóng)業(yè)數(shù)據(jù)中地貌類(lèi)型、作物種類(lèi)等均可賦予不同的整數(shù)來(lái)代表不同的類(lèi)型。

1.2 相似性度量

1.2.1 數(shù)值型屬性數(shù)據(jù)

數(shù)值型數(shù)據(jù)相似性測(cè)度通常采用距離測(cè)度，比如切氏距離、馬氏距離、Caberra距離和平均距離等方法。一般情況下，由于數(shù)值型數(shù)據(jù)量綱、來(lái)源、量級(jí)均不相同，所以計(jì)算距離前應(yīng)進(jìn)行標(biāo)準(zhǔn)化處理。數(shù)據(jù)的歸一化處理是最典型的，將數(shù)據(jù)統(tǒng)一映射到[0，1]區(qū)間上，常用的標(biāo)準(zhǔn)化方法有離差標(biāo)準(zhǔn)化、標(biāo)準(zhǔn)差標(biāo)準(zhǔn)化等。

1.2.2 二元型屬性數(shù)據(jù)

二元型屬性數(shù)據(jù)相似性度量通常采用匹配測(cè)度[1]。對(duì)于2個(gè)分別包含d維二元屬性的空間實(shí)體P和Q，其中任一分量pi和qi的比較將構(gòu)成以下4個(gè)變量。

1）f00：pi為0且qi也為0的屬性個(gè)數(shù)；

2）f01：pi為0且qi也為1的屬性個(gè)數(shù)；

3）f10：pi為1且qi也為0的屬性個(gè)數(shù)；

4）f11：pi為1且qi也為1的屬性個(gè)數(shù)。

此時(shí)的匹配方法有以下幾種簡(jiǎn)單匹配系數(shù)：Jaccard系數(shù)、Tanimoto系數(shù)、Dice系數(shù)以及Kulzinsky系數(shù)等，最常用的是Jaccard系數(shù)，算法如下：對(duì)于2個(gè)分別包含d維二元屬性的空間實(shí)體P和Q，其Jaccard系數(shù)記為J（P，Q），即

J（P，Q）=f11/（f01+f10+f11） 。 （6）

1.2.3 類(lèi)型屬性數(shù)據(jù)

類(lèi)型屬性數(shù)據(jù)通常采用一種簡(jiǎn)單的相似系數(shù)，根據(jù)二元屬性的定義，2個(gè)空間實(shí)體P和Q，如果這2個(gè)實(shí)體中的分量（pi和qi）相等的個(gè)數(shù)為m，分量總個(gè)數(shù)為n，則類(lèi)型相似系數(shù)L（P，Q）=m/n。

2 屬性數(shù)據(jù)相異度度量

相異度度量是根據(jù)混合屬性相異度的需要，在相似性度量的基礎(chǔ)上建立起來(lái)的混合度量方法。

2.1 數(shù)值型距離相異度

數(shù)值型數(shù)據(jù)距離相異度，就是在數(shù)值上相距的遠(yuǎn)近，通常采用歐式距離和歐式距離平方等方法，而K-prototypes聚類(lèi)方法中數(shù)值屬性數(shù)據(jù)就是采用歐幾里平方的方法計(jì)算數(shù)值相異度。

當(dāng)然，計(jì)算前要對(duì)數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理，處理后一般為小數(shù)，處于（0～1）之間，此時(shí)K-prototypes聚類(lèi)算法不僅要計(jì)算數(shù)值型數(shù)據(jù)，而且要計(jì)算分類(lèi)型數(shù)據(jù)，yes或者no型數(shù)據(jù)轉(zhuǎn)化為二元數(shù)據(jù)，其他字符串型（非數(shù)字）數(shù)據(jù)轉(zhuǎn)化為類(lèi)型數(shù)據(jù)。

2.2 二元型相異度

根據(jù)二元型屬性數(shù)據(jù)相似性度量中的匹配系數(shù)，不難想到二元相異度系數(shù)即為相似度的對(duì)立面公式為

J反（P，Q）=1-f11/（f01+f10+f11） 。 （7）

取相異度系數(shù)與二元單維屬性總個(gè)數(shù)（Num）的算術(shù)平方根相乘作為二元相異度距離，即為J反（P，Q）·。

2.3 類(lèi)型屬性相異度

同樣對(duì)于類(lèi)型屬性數(shù)據(jù)相異度系數(shù)的定義為

L反（P，Q）=1-m/n 。 （8）

當(dāng)然取相異度系數(shù)與二元單維屬性總個(gè)數(shù)的算術(shù)平方根相乘作為類(lèi)型相異度距離，即為L(zhǎng)反（P，Q）·。

3 K-prototypes算法的改進(jìn)

對(duì)于K-prototypes算法中數(shù)值型數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理后依然選用歐幾里平方來(lái)計(jì)算距離相異度

d1（Xi，Vl）=∑Xij－Vlj。 （9）

對(duì)于二元和類(lèi)型屬性數(shù)據(jù)則采用相異度系數(shù)的方法計(jì)算

d2（Xi，Vl）=J反（P，Q）·， （10）

d３（Xi，Vl）=Ｌ反（P，Q）·。 （11）

然后引入β和γ兩個(gè)參數(shù)，對(duì)聚類(lèi)過(guò)程中二元屬性和類(lèi)型屬性的權(quán)重進(jìn)行控制。令X={X1，X2，X3，…，Xn}表示具有n個(gè)樣本的數(shù)據(jù)集，其中Xi=[Xi1，Xi2，…，Xip，Xi（p+1），…，Xim，Xim+1，…，XiH]表示第i個(gè)樣本的H個(gè)屬性值（1至p為數(shù)值型數(shù)據(jù)屬性，p+1至m為二元數(shù)據(jù)屬性，m+1至H為類(lèi)型數(shù)據(jù)屬性）。令k為數(shù)據(jù)集的初始聚類(lèi)數(shù)，對(duì)應(yīng)模的集合為V={V1，V2，…，Vk}，迭代聚類(lèi)集為C={C1，C2，…，Ck}，Ci= [Ci1，Ci2，…，Cik］，具體步驟：①首先明確類(lèi)的個(gè)數(shù)k，并為每個(gè)類(lèi)選擇k個(gè)初始的聚類(lèi)原型；②根據(jù)改進(jìn)后的K-prototypes聚類(lèi)公式，對(duì)樣本到各原型距離進(jìn)行計(jì)算，依據(jù)計(jì)算結(jié)果，把樣本劃分到距離最近的聚類(lèi)原型相應(yīng)的聚類(lèi)中；③對(duì)聚類(lèi)原型全部進(jìn)行重新計(jì)算；④循環(huán)③及④，直至各個(gè)聚類(lèi)中數(shù)據(jù)對(duì)象趨于穩(wěn)定不變，方可停止。

于是改進(jìn)后的K-prototypes算法

式中：β和γ分別為二元和類(lèi)型屬性數(shù)據(jù)的權(quán)重值（0～1）。

不難看出，當(dāng)沒(méi)有分類(lèi)型數(shù)據(jù)時(shí)，即β=0，γ=0時(shí)，該算法即為K-means算法；當(dāng)沒(méi)有二元數(shù)據(jù)時(shí)，即β=γ時(shí)，該算法與K-prototypes算法相似，但其實(shí)并不相同。

4 改進(jìn)后K-prototypes聚類(lèi)算法實(shí)現(xiàn)與結(jié)果分析

4.1 數(shù)據(jù)選擇和計(jì)算

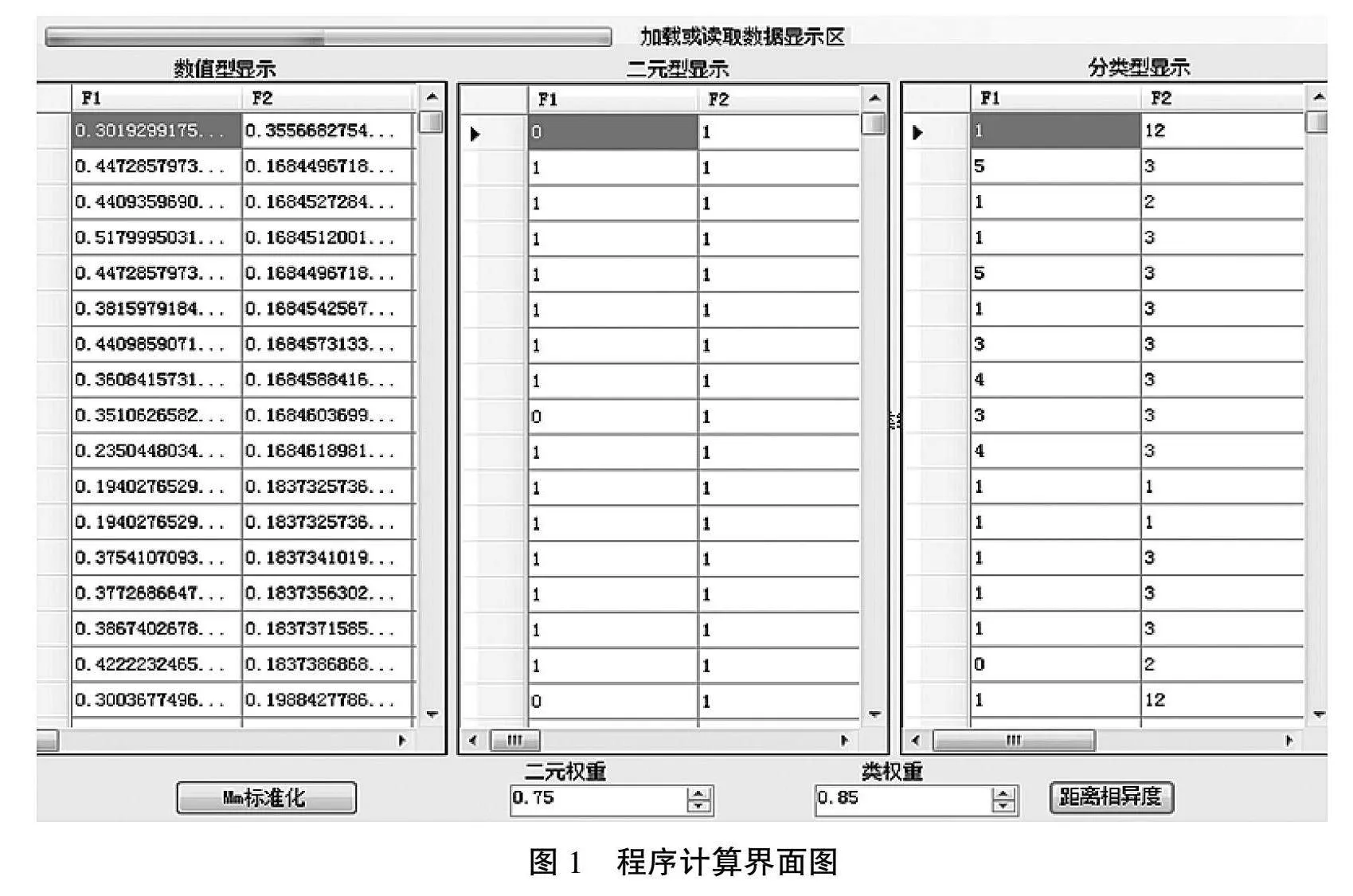
屬性數(shù)據(jù)選用全國(guó)農(nóng)業(yè)種植統(tǒng)計(jì)數(shù)據(jù)（2 368個(gè)城（縣、區(qū)），每個(gè)區(qū)域包含37個(gè)數(shù)值型數(shù)據(jù)，12個(gè)二元數(shù)據(jù)，4個(gè)類(lèi)型數(shù)據(jù)），數(shù)值型數(shù)據(jù)標(biāo)準(zhǔn)化后計(jì)算過(guò)程如圖1所示。

4.2 改進(jìn)方法聚類(lèi)結(jié)果與分析

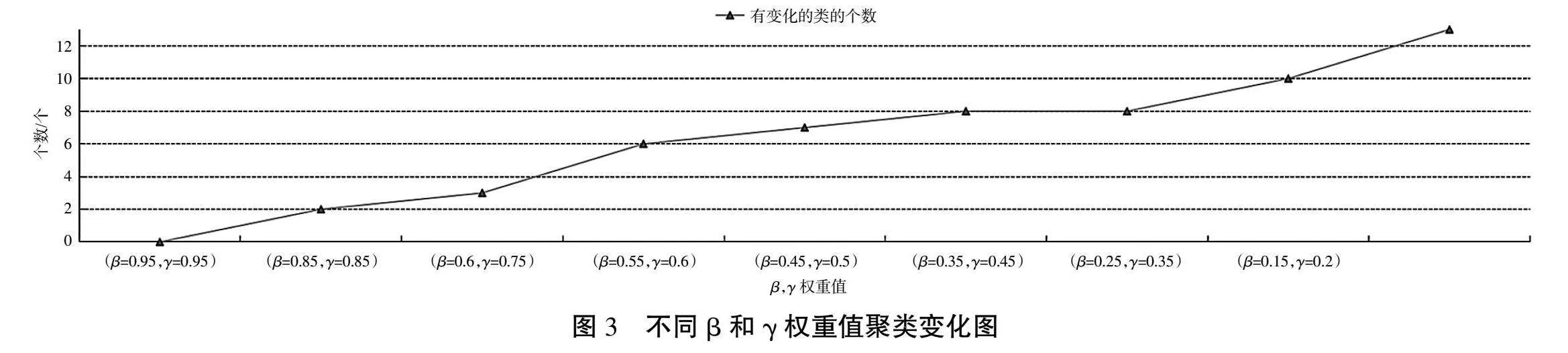
為了方便比較和分析，本次選擇34個(gè)代表縣區(qū)的所有屬性數(shù)據(jù)作為處理對(duì)象。當(dāng)β=1，γ=1，k=13時(shí)，聚類(lèi)結(jié)果如圖2所示。隨著β和γ值的變化，有變化的聚類(lèi)個(gè)數(shù)如圖3所示。

如圖3所示，標(biāo)準(zhǔn)化后的數(shù)值型數(shù)據(jù)均在0～1，經(jīng)過(guò)歐幾里平方相加后數(shù)據(jù)不會(huì)太大，分類(lèi)數(shù)據(jù)屬性相異度距離有效降低了分類(lèi)數(shù)據(jù)的2個(gè)權(quán)重值在聚類(lèi)過(guò)程中在某一范圍內(nèi)大幅度改變聚類(lèi)結(jié)果的影響，因此還是要根據(jù)不同要求選擇合理的權(quán)重值。

5 結(jié)束語(yǔ)

本研究從數(shù)據(jù)標(biāo)準(zhǔn)化和分類(lèi)數(shù)據(jù)細(xì)化方面，對(duì)屬性數(shù)據(jù)的計(jì)算進(jìn)行改進(jìn)，特別是將分類(lèi)數(shù)據(jù)劃分為二元數(shù)據(jù)和類(lèi)型數(shù)據(jù)，滿足和方便了用戶對(duì)不同類(lèi)型數(shù)據(jù)的重要性和影響程度進(jìn)行操控，實(shí)現(xiàn)理想的分類(lèi)結(jié)果，對(duì)混合屬性聚類(lèi)分析有一定的指導(dǎo)意義。當(dāng)然，后期還可以對(duì)K-prototypes聚類(lèi)算法的其他問(wèn)題和局限進(jìn)行探討，比如初始中心點(diǎn)選擇、全局性等方面。

參考文獻(xiàn)：

[1] 鄧敏，劉啟亮，李光強(qiáng)，等.空間聚類(lèi)分析及應(yīng)用[M].北京：科學(xué)出版社，2177.0101.

[2] 陳治平，林亞平，彭雅，等.基于最小無(wú)關(guān)類(lèi)的數(shù)據(jù)挖掘算法[J].電子學(xué)報(bào)，2003，31（11）1750－1754．

[3] CHEN N，CHEN A，ZHOU L X.Fuzzy K-prototypes algorithm for clustering mixed numeric and categorical valued data[J].Journal of Software，2001.12（8）1107－1119．

[4] 孫吉貴，劉杰，趙連宇.聚類(lèi)算法研究[J].軟件學(xué)報(bào)，2008，19（1）48－61．

[5] HUANG Z. Extensions to the K-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery II，1998（2）283－304．

[6] Huang Z.， Ng M. A fuzzy K-modes algorithm for clustering categorical data[J].IEEE Transacitons on Fuzzy Systems，1999，7（4）：446－452．

[7] 趙立江，黃永青，劉玉龍.改進(jìn)的混合屬性數(shù)據(jù)聚類(lèi)算法[J].計(jì)算機(jī)工程與設(shè)計(jì)，2007，28（20）：4850－4852．

[8] 陳丹，王振華.一種改進(jìn)的混合屬性數(shù)據(jù)聚類(lèi)算法[J].電腦知識(shí)與技術(shù)，2010，6（11）：2713-2716.

[9] 陳韡，王雷，蔣子云，等.基于K-prototypes的混合屬性數(shù)據(jù)聚類(lèi)算法[J].計(jì)算機(jī)應(yīng)用，2010，30（8）：2003-2005.

[10] 白天，冀進(jìn)朝，何加亮，等.混合屬性數(shù)據(jù)聚類(lèi)的新方法[J].吉林大學(xué)學(xué)報(bào)（工學(xué)版），2013，43（1）：130-134.

[11] 劉強(qiáng)，鄧?yán)冢Z振紅，等.一種改進(jìn)的加權(quán)K-prototypes算法[J].激光雜志，2014，35（1）：18-20.