基于Bloom Filter本地差分隱私的基數估計

摘 要：計算機技術和通信技術的共同發展，使得數據呈現指數大爆炸式的增長。數據中蘊含的巨大價值是有目共睹的。但是對數據集的肆意收集與分析，使用戶的隱私數據處在被泄露的風險中。為保護用戶的敏感數據的同時實現對基數查詢的有效響應，提出一種基于差分隱私的隱私保護算法BFRRCE（Bloom Filter Random Response for Cardinality Estimation）。首先對用戶的數據利用Bloom Filter數據結構進行數據預處理，然后利用本地差分隱私的擾動算法對數據進行擾動，達到保護用戶敏感數據的目的。

關鍵詞：隱私保護；本地化差分隱私；Bloom Filter；基數；隨機響應

中圖分類號：TP309 文獻標志碼：A 文章編號：2095-2945（2024）28-0035-04

Abstract： The joint development of computer technology and communication technology has led to exponential explosive growth in data. The huge value contained in the data is obvious to all. However， the wanton collection and analysis of data sets puts users 'private data at risk of being leaked. In order to protect users 'sensitive data while achieving effective responses to cardinality queries， this paper proposes a privacy protection algorithm， BFRRCE（Bloom Filter Random Response for Cardinality Estimation）， based on differential privacy. First， the user's data is preprocessed using the Bloom Filter data structure， and then the data is disturbed using a local differential privacy perturbation algorithm to achieve the purpose of protecting the user's sensitive data.

Keywords： privacy protection; localized differential privacy; Bloom Filter; cardinality; random response

隨著信息技術和網絡技術的迅速發展，數據的類型和數據量在不斷地增長。大數據驅動的管理與決策發展核心是不同行業領域之間的數據資源開放，目前大數據貫穿七大行業：商務、金融、醫療健康、教育、交通、電力以及石油業天然氣[1]。但數據的開放和共享必然會帶來隱私數據保護的問題。

保護隱私的技術有很多種，如匿名化技術[2]、加密技術[3]等，但是它們都是基于攻擊者知識背景的改變而進行改進，且無法提供可量化的隱私保證。基于上述原因，差分隱私[4-5]被Cynthia Dwork提出。

基數是一個十分重要的數據集的數字特征。近年來對于數據集進行估計的方法大致可以分為3大類：第一類是基于概要的方法得到的，文獻[6]是利用概率統計的方法做的，本文并未涉及隱私保護，但蘊含著PCSA sketch的核心思想，其思想在文獻[7]和文獻[8]中都有體現，文獻[7]只是針對2個數據集，即2個用戶的基數估計，且其擾動概率的設置使得其基數查詢的精度并不高。文獻[8]提出了2種方法，一個是確定性合并同樣也是針對2個用戶的數據進行保護的，所以當面對多用戶時是不可行的。第二種方法是隨機性合并，它可以處理多用戶的基數估計，但是在用戶數較多時，算法所需的擾動概率矩陣在運算時是會經常溢出的。第二類是基于采樣的方法。涉及到的文獻[9]是基于采樣的方法，因為只利用了數據集的部分信息，所以基數估計的誤差相對來說還是很大的，且文獻沒有涉及到隱私保護。第三類是基于學習型基數估計的方法。涉及到的文獻[10]是通過無監督學習學到一個與負載無關的模型來近似極大似然估計，且文獻中同樣未涉及隱私保護。為了彌補上述問題，提出了一個基于Bloom Filter本地差分隱私的基數估計算法。

1 相關知識背景

1.1 基數查詢

基數：在數學上被用來描述集合的大小，是指一個集合中不重復的元素的數量。例如數據集A中雖然有{a，a，b，b，c}，但是它的基數是3，因為數據集A中只有a、b以及c 3類數據。

對數據集進行基數查詢有十分重要的意義。以廣告商投放廣告費為例，第一次廣告商在APP1、APP2和APP3 3個平臺上投放廣告，投放的廣告費分別為2萬元、3萬元以及5萬元。但是經過統計發現在3個平臺觀看廣告的用戶的基數分別為50萬人、20萬人和10萬人，基數和為52萬人。觀察可以發現廣告費在APP2和APP3投放得到的結果是不如意的，因此我們可以通過上述結果去調整廣告費的投放方案。因此進行基數估計是有現實意義的。

1.2 本地化差分隱私模型

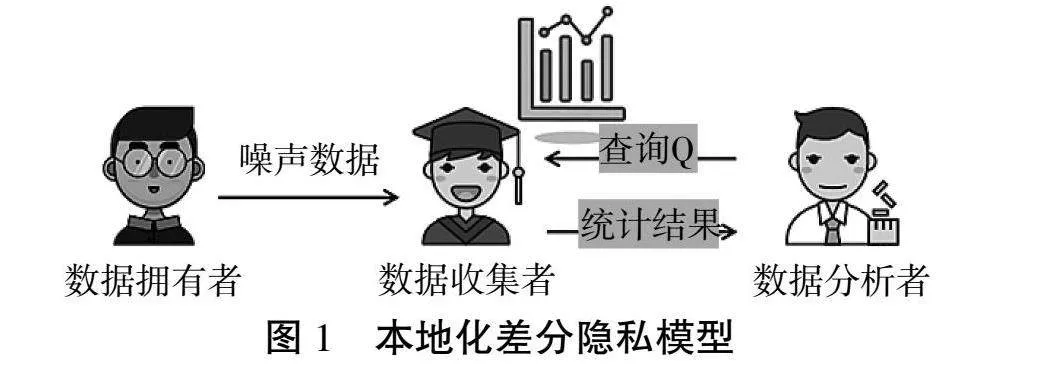
與傳統的隱私保護技術相比，差分隱私保護技術[4]假設攻擊者擁有最強的知識背景。差分隱私保護技術常用的模型有中心化差分隱私保護模型[5]和本地化差分隱私保護模型[11]。本文使用的是本地化差分隱私保護模型。本地化差分隱私模型中包含3個關鍵的角色：數據擁有者（用戶）、數據收集者以及數據分析者。本地化差分隱私模型下假設擁有者對數據收集者是不信任的，所以數據擁有者自己將自己的數據通過本地化差分隱私的擾動機制將自己的數據加噪后得到的噪聲數據發送給數據收集者。數據收集者對所有數據擁有者發送的數據進行統計分析，然后將統計結果發送給數據分析者，以此響應查詢數據分析者的查詢請求，如圖1所示。

定義1（本地化差分隱私）。對于任意2個不同的值？淄和？淄′，在隱私算法M的作用下得到相同輸出的概率滿足下列不等式時，隱私算法M滿足ε-本地化差分隱私。

， （1） 式中：P表示概率；y表示隱私算法作用在值v之后得出的噪聲值；e表示自然對數的底數值，為2.718 28；ε代表隱私預算，而隱私預算越小，則意味著隱私保護程度越高[11]。

1.3 隨機響應機制

本文使用的隱私算法為RR[12]。RR算法是Warner在1965年提出的，是一種十分經典的隱私保護算法。它是針對二類敏感問題（答案只有“yes”或者“no”）提出的隱私保護算法，核心思想是利用用戶對敏感問題回答的不確定性來保護用戶的敏感數據。一個經典的例子，要調查n個用戶中患有糖尿病的占比，顯然這個問題對于用戶來說是敏感的，答案只有“yes”或者“no”。用戶在回答問題前拋出硬幣，正面朝上的概率為p，用戶真實回答問題；反面朝上的概率為1-p，用戶非真實回答問題。當然為了使統計信息是可用的通常p是大于0.5的。通過這種不確定性RR隱私算法保護了用戶的敏感信息。數據收集者將收集到用戶的回答，經統計發現回答yes的有n1個，假設實際的患有糖尿病的有nyes個。

根據概率論相關知識可知

， （2）

由極大似然估計可知

根據定義1的公式（1）計算，要想RR機制滿足本地化差分隱私p要滿足條件

所以符合本地化差分隱私的RR隱私算法可以用以下公式表示

。 （5）

1.4 Bloom Filter結構

本文使用的存儲結構為Bloom Filter是由0/1組成的向量，可以用來檢測一個元素是不是存在于集合中，因此也可用于去重。它是利用哈希函數，將一個元素映射到一個長度為L的數組上的一個bit上，當這位是1時，那么這個元素在集合中。反之，則不在集合內。這個方法的缺點是當檢測的元素很多的時候可能有沖突，解決的辦法就是使用k個哈希函數對應k個bit，如果所有的bit 都是1的話，那么元素在集合內，如果有0的話，元素則不在集合內。

2 BFRRCE算法

2.1 BFRRCE算法的偽代碼

輸入：n個用戶的數據，長度為L的，有l個哈希函數的Bloom Filter B。隱私預算ε。

輸出：滿足本地化差分隱私的基數查詢ce。

數據分析者初始化好B之后將其發送給所有的數據擁有者。

數據擁有者端：

1）For每一個數據擁有者do：

2）將自己的值？淄i映射到B中記作Bi。

3）對Bi的每一位獨立的使用RR擾動機制得到。

4）將發送給數據收集者。

數據收集者端：

5）將收集到的所有數據擁有者發送的報告按列相加并校正來重構Bloom Filter B″。

6）對范圍內的所有數據逐個檢驗是否在數據集中，在ce=ce+1。

7）Return ce。

2.2 BFRRCE算法的隱私性和可用性證明

定理1即BFRRCE滿足ε-本地化差分隱私。

因為Bloom Filter有l個哈希函數。所以任意2個用戶的值最多有2l個bit位不同，由定義1可知BFRRCE要想滿足ε-本地化差分隱私，需要證明BFRRCE機制滿足下列不等式

所以只需要對Bloom Filter的每一位按位擾動，擾動概率如下列公式所示時，BFRRCE滿足ε-本地化差分隱私。

式中：Pr表示事件發生的概率，j表示構造出的Bloom Filter矩陣B這個數據結構的第j列。

定理2即BFRRCE算法得到的估計是無偏的，即E（（ΣBi[j]））=C（ΣBi[j]），E為期望。

C（ΣBi[j]）表示不經過隱私算法保護，數據收集者將所有Bloom Filter按列求和后得到的重構的Bloom Filter的第i個bit位的真實計數。（ΣBi[j]）表示數據收集者將所有的噪聲Bloom Filter按列求和后得到的重構的Bloom Filter得到的第i個bit位的估計計數。

證明：假設B″[j]表示數據收集者對所有數據擁有者發來的Bloom Filter的按列求和后得到的重構Bloom Filter中第i個bit位觀測值。

。（8）

求解式（8）可得

所以（ΣBi[j]）的期望值為

由公式（8）可得

3 應用實驗

3.1 實驗環境和數據

硬件環境為8 GB內存、4核Intel CPU（4 GHz），Windows 10操作系統上運行。算法是采用Python語言實現的，并使用MATLAB軟件繪制數據結果的圖。

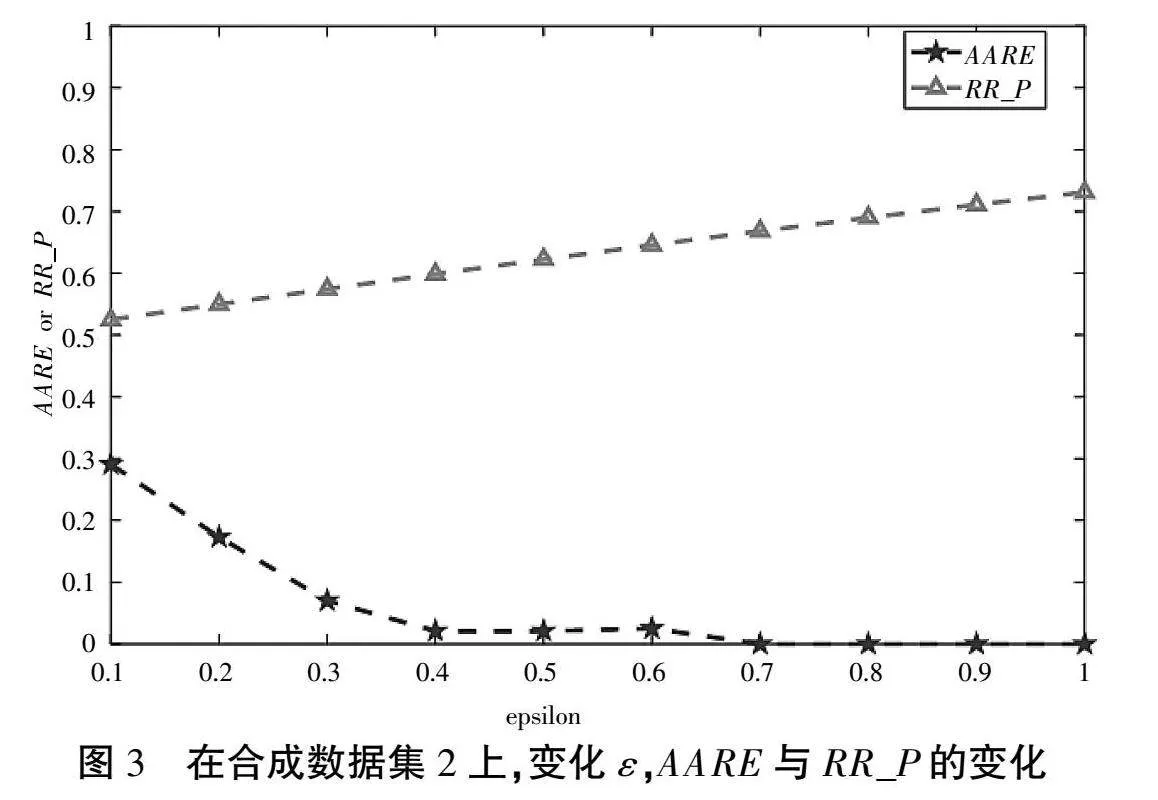
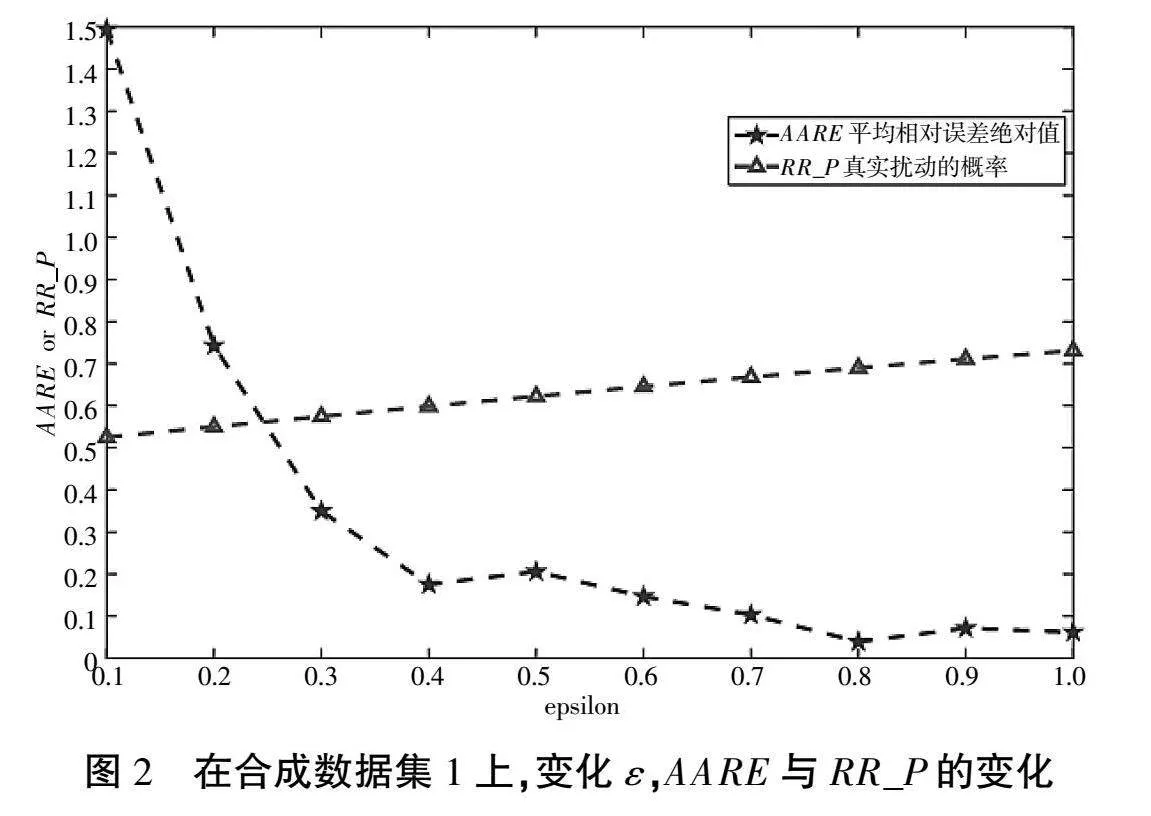
論文是在合成數據集和比特幣交易信息的真實數據集上做的。合成數據集1的基數ce為122，數據量為2 000。合成數據集2的真實基數ce為122，數據量大小為10 000。

3.2 實驗方法

本文采用的是用平均相對誤差絕對值對文中提出的算法進行度量的。

式中：ce表示數據集的真實基數值，e表示對數據集基數值ce的估計值，所以AARE越小說明算法的精度就越高，越大說明算法的精度就越低。

3.3 實驗結果

觀察圖2和圖3可以發現，隨著ε的增大，真實擾動的概率RR_P也增大，基數估計的精度就越高，平均相對誤差總體呈遞減的趨勢。

當ε小于等于0.3時，平均相對誤差是相對較高的，其原因是當ε小于等于0.3時真實擾動的概率RR_P接近于0.5，可以理解為被問二類敏感問題的受訪者隨機說了一個答案，沒有提供任何有用的信息。

當ε大于等于0.4時，真實擾動的概率RR_P是近似大于等于0.6的，受訪者回答的信息是更可用的，因此平均相對誤差絕對值是較小的，基數估計的精度是較高的。

4 結論

本文通過分析當前數據收集與分析面臨的問題提出了BLRRCE算法在保護用戶敏感數據的同時，實現了對數據集的基數查詢。為差分隱私技術的推廣以及服務商為用戶提供更人性化服務起到了正向的影響。

參考文獻：

[1] 張嘯劍.差分隱私理論與實踐[M].北京：經濟管理出版社，2021.

[2] LATANYA S. k-anonymity： a model for protecting privacy[J]. International Journal of Uncertainty， Fuzziness and Knowledge-Based Systems，2002，Volume 10Issue 5：557-570.

[3] STEHLE D， STEINFELD R. Faster fally homomorphic encryption[C]// Proc of the 16th Int Conf on the Theory and Application of Cryptology and Information Security. Berlin：springer， 2010：377-394.

[4] CYNTHIA D， AARON R. The Algorithmic Foundations of Differential Privacy[J]. Found. Trends Theor. Comput. Sci. 2014，9（3-4）： 211-407.

[5] DWORK C. Differential Privacy[C]// Proc of the 33rd Int Colloquium on Automata， Languages and Programming， 2006：1-12.

[6] FLAJOLET P， MARTIN G. N. Probabilistic counting algorithms for data base applications[J]. Journal of Computer and System Sciences，1985，31（2）：182-209.

[7] RASMUS P， NINA M S. Efficient Differentially Private F0Linear Sketching[C]//arXiv：2001.11932 [cs. DS]， Jan 2020.

[8] GRAHAM C， JONATHAN H. Sketch-Flip-Merge： Mergeable Sketches for Private Distinct Counting[C]// Proceedings of the 40th International Conference on Machine Learning Proceedings of Machine Learning Research 2023：12846-12865.

[9] LI J J， WEI Z W， DING B L， et al. Sampling-based Estimation of the Number of Distinct Values in Distributed Environment[C]//In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining（KDD '22）.2022：893-903.

[10] WU R Z， DING B L， CHU X， et al. Learning to be a statistician： learned estimator for number of distinct values[C]//Proceedings of the VLDB Endowment，2022，15（2）：272-284.

[11] DWORK C. Differential Privacy：A Survey of Results[C]// Proc of the 5th Int Conf on Theory and Applications of Models of Computation， 2008：1-19.

[12] WARNER S L. Randomized response： A survey technique for eliminating evasive answer bias[J]. Journal of the American Statistical Association， 1965， 60（309）： 63-69.