一種新的高速運動目標雷達相干積累方法

摘 要：該文針對高速運動目標雷達相干積累中的跨距離單元走動問題，提出一種基于時頻反轉互相關及尺度逆傅里葉變換的聯合算法。首先通過時頻反轉互相關分離出目標距離信息，之后使用測得的距離信息構造補償函數，并使用尺度逆傅里葉變換消除跨距離單元走動，得出目標徑向速度。經過仿真實驗可以證明，該文算法能夠在不進行任何參數搜索的條件下實現對具備跨距離單元走動和速度模糊的高速運動目標進行回波能量積累，獲得目標的徑向距離和速度信息，且具備較低的運算復雜度。

關鍵詞：高速目標；雷達；距離徙動校正；長時間相干積累；徑向距離

中圖分類號：TN957 文獻標志碼：A 文章編號：2095-2945（2024）28-0047-04

Abstract： Aiming at the problem of walking across range cells in coherent accumulation of radar echoes from high-speed moving targets， this paper proposes a joint algorithm based on time-frequency inversion cross-correlation and inverse scale Fourier transform. First， the target range information is separated through time-frequency inversion cross-correlation， and then the measured range information is used to construct a compensation function， and inverse scale Fourier transform is used to eliminate walking across range cells to obtain the target radial velocity. Simulation experiments show that the algorithm can accumulate echo energy from high-speed moving targets with cross-range cell walking and velocity ambiguity without any parameter searching， obtain the radial range and velocity information of the target， and has low computational complexity.

Keywords： high-speed target; radar; range migration correction; long-term coherent integration; radial range

在雷達目標探測中，長時間相干積累作為提升信噪比和弱小目標檢測性能的手段cJj0BnGLeUS3qcya+X2gPCEB+EEwUPHUh/ITNuAA+E8=得到了廣泛應用。而高速目標雷達回波受到目標高徑向速度影響，可能存在跨距離單元走動，從而使傳統運動目標檢測（Moving Target Detection，MTD）算法[1]失效。如何克服跨距離單元走動和多普勒頻率徙動影響，快速實現回波能量積累與目標檢測，是雷達信號處理領域的熱門話題[2]。

在已提出的高速運動目標相干積累算法中，最為成熟的Keystone變換[3]和RFT（Radon Fourier Transform）算法[4-6]能夠在低信噪比條件下實現有效相干積累。但Keystone變換對跨距離單元走動的校正會受速度模糊影響，需要進行模糊數搜索。而RFT算法需要對目標運動參數進行遍歷搜索，計算量巨大。

本文在前人研究基礎上，針對勻速運動模型，提出了一種基于時頻反轉互相關（Time-Frequency domain Reverse Cross-correlation， TFRC）[7]與尺度逆傅里葉變換（Scaled Inverse Fourier Transform， SCIFT）[8]的相干積累方法，通過2種算法相互配合，可以不進行參數搜索校正線性距離徙動并估計目標運動參數。通過在距離頻域-慢時間域進行距離頻率和慢時間的雙重反轉，消除回波跨距離走動影響，并獲得目標徑向距離。

使用獲得的徑向距離構造補償函數，并使用SCIFT實現跨距離單元走動校正域信號能量積累，獲得目標徑向速度信息。且在滿足一定條件時，可以排除目標速度模糊的影響，獲得目標真實徑向速度。

1 信號模型及問題表述

設雷達發射的線性調頻信號為

式中：fc為信號載頻；Tp為脈沖持續時間；B為信號帶寬，k=B/Tp為信號調頻率；為距離向快時間；tm=mTr為慢時間，其中，Tr為脈沖重復周期；t=+tm為全時間。

設目標初始距離為R0，速度為？淄。此時，雷達第m個發射脈沖所對應的信號回波時延可以近似為

？子m＝２（R0+？淄tm）/c=２（R0+？淄mTr）/c 。 （2）

而雷達接收的第m個脈沖的回波信號可以表示為

式中：Ar為目標后向散射系數。對回波信號進行脈沖壓縮處理后，可以得到如下形式的信號表達式

式中：A1為脈沖壓縮后的回波信號幅度。由式（4）可知，回波包絡的峰值位于=2R（tm）/c 處，目標回波峰值位置隨著慢時間tm發生變化，即發生了距離走動。

當回波距離走動在相干積累時間內超過一個距離單元時，發生跨距離單元走動，此時使用MTD算法直接進行相干積累，回波能量分散在不同距離單元中，降低積累增益檢測性能。

2 快速相干積累方法

2.1 基于序列反轉的高速機動目標回波積累方法

對于高速目標探測中可能會出現速度模糊的情況，目標的徑向速度可以重寫為？淄=？淄0+Nb？淄b，其中雷達盲速？淄b=？姿·ＰＲＦ/2；？淄0為模糊速度且？淄0<？淄b/2；Nb為多普勒模糊數。此時將？淄=？淄0+Nb？淄b代入式（4），對式（4）進行快時間維度的FFT，得到距離頻域回波脈壓信號的表達式如下

（5）

由式（5）可知，跨距離單元走動在快時間頻域表現為距離頻率f與慢時間tm之間的耦合，為了解決跨距離單元走動問題對相干積累的影響，本文提出了基于序列反轉和尺度逆傅里葉變換的高速目標回波積累方法。

設經過脈沖壓縮后的回波信號Sc（f，tm）。其中包括的M+1個脈沖（M為偶數）所組成的慢時間序列tm=mTr表示為

同理，回波信號的距離頻率序列f=n？駐f表示為（其中N為偶數，？駐f為距離頻域采樣間隔）

將式（6）和（7）代入式（5）可得到回波距離頻域脈壓信號離散表達式

（8）

對式（8）中Ｓc（n，m）同時進行慢時間維序列反轉和距離頻率序列反轉，得到Ｓc（，）。慢時間反轉序列和距離頻率序列反轉可以分別表示為

求Ｓc（，）的共軛運算，得到的信號如下所示

文獻[7]提出了一種基于時頻反轉互相關和對稱時移雙重自相關的高速機動目標信號相干積累方法，應用于三階運動目標檢測，將其中的時頻反轉互相關運算引入到本文勻速運動目標檢測場景中來，以實現目標徑向距離的快速獲取。如式（12）所示

由式（12）可知，當時頻反轉互相關用于勻速運動目標的處理時，可以校正回波中的跨距離單元走動。

對式（12）中的信號結果進行距離維IFFT變換至距離時域，得到結果以連續形式表示如下

時頻反轉互相關運算后，式（13）中信號包絡峰值位置只與目標的距離有關，跨距離單元走動被成功校正，可以直接通過慢時間方向的FFT實現相干積累。然而，受到速度模糊影響，積累后得到的相干積累峰值在多普勒維的坐標對應值為目標模糊速度，這意味著時頻反轉互相關算法運用于高速目標相干積累時受到限制，無法獲取目標全部運動信息。

為了克服速度模糊影響，獲得目標真實速度信息，使用由時頻反轉互相關運算得到的目標距離R0構建補償函數

對式（5）中的脈壓后距離頻域信號Ｓc（f，tm）做相位補償得

對式（15）進行SCIFT可以得到

式中：？濁為縮放因子；t？鬃為經過尺度變換的距離向快時間。SCIFT處理后信號包絡峰值沿著直線t？鬃=2？淄/？濁c分布，不再隨慢時間變化。縮放因子的選擇應滿足使得經過SCIFT后的信號包絡峰值位置不超過快時間的最大值。對式（16）通過慢時間方向FFT可實現相干積累如式（17）所示，并可通過峰值檢測獲得目標速度。

2.2 基本算法流程及運算復雜度分析

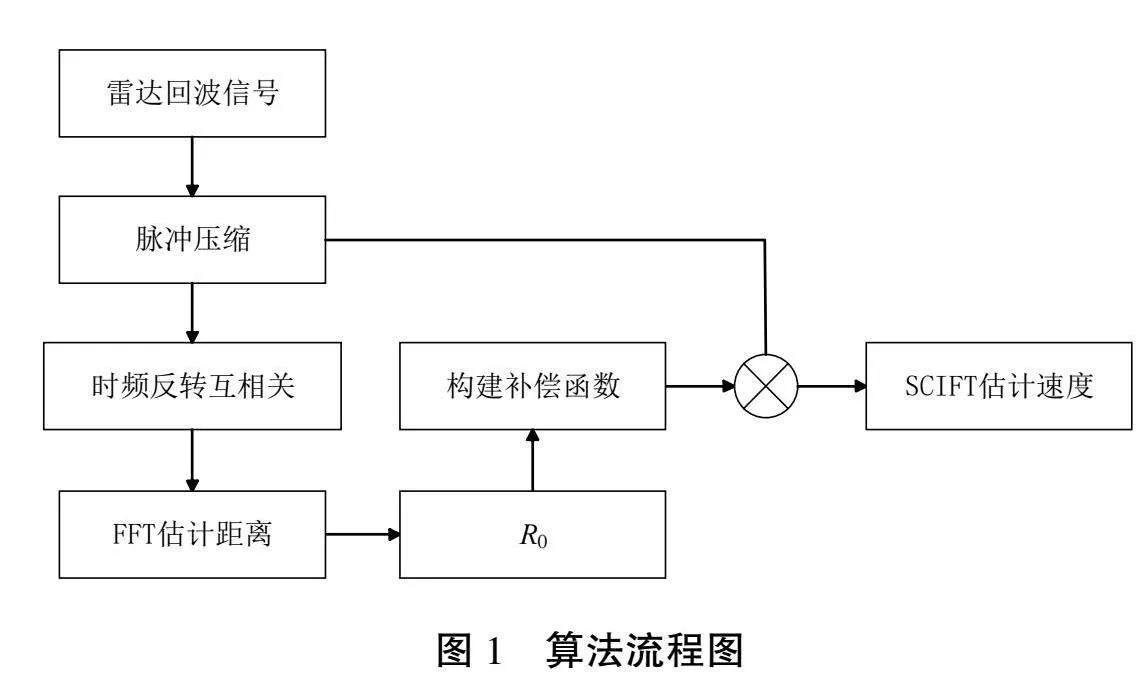
通過本文提出的算法估計高速機動目標運動參數的流程如圖1所示。

由圖1可知，本文算法首先采用時頻反轉互相關變換實現回波信號跨距離單元走動的校正，在完成校正后實現能量積累，獲得目標距離信息。其中，時頻反轉互相關運算通過一次矩陣復乘實現。設回波積累脈沖數為Ｍ，快時間距離門數為Ｎ，則一次矩陣乘法所需要的運算復雜度為Ｏ（MN）。而在本文提取目標徑向距離時進行能量積累所需的慢時間FFT運算復雜度為Ｏ[（MNlog2M）/2]。

而對于回波補償函數的構建及相位補償操作同樣僅由矩陣乘法實現。低于后續用于估計目標真實速度的SCIFT，也可以通過Chirp-z變換實現，進而減小所需的運算量。

使用Chirp-z變換實現時，SCIFT可以視作是頻域卷積，可以通過IFFT實現。此時SCIFT所需的計算復雜度為Ｏ[（3MNlog2Ｎ）/２]。綜上，TFRC-SCIFT所需的計算復雜度量級為Ｏ[2MNlog2M]。

本文提出的算法實現僅需復數乘法與FFT和IFFT，不需要參數搜索，更有利于工程實現。

3 仿真實驗

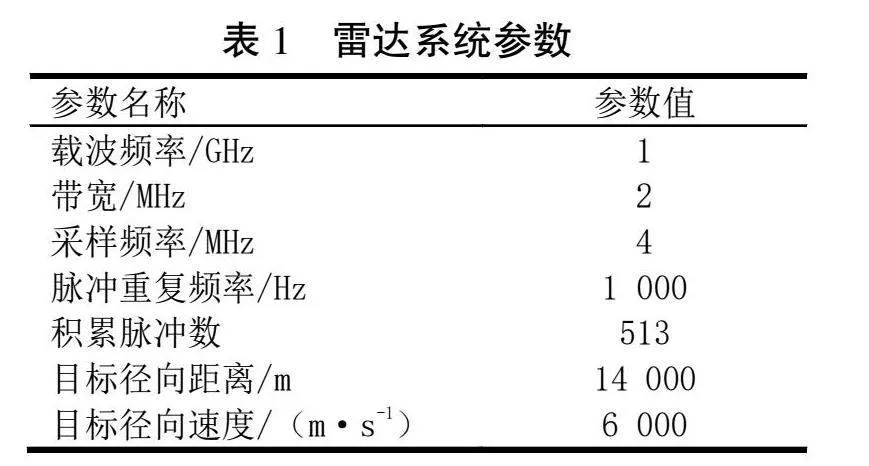
本節通過數值仿真驗證提出算法的有效性。設雷達系統參數，即仿真目標運動參數見表1。

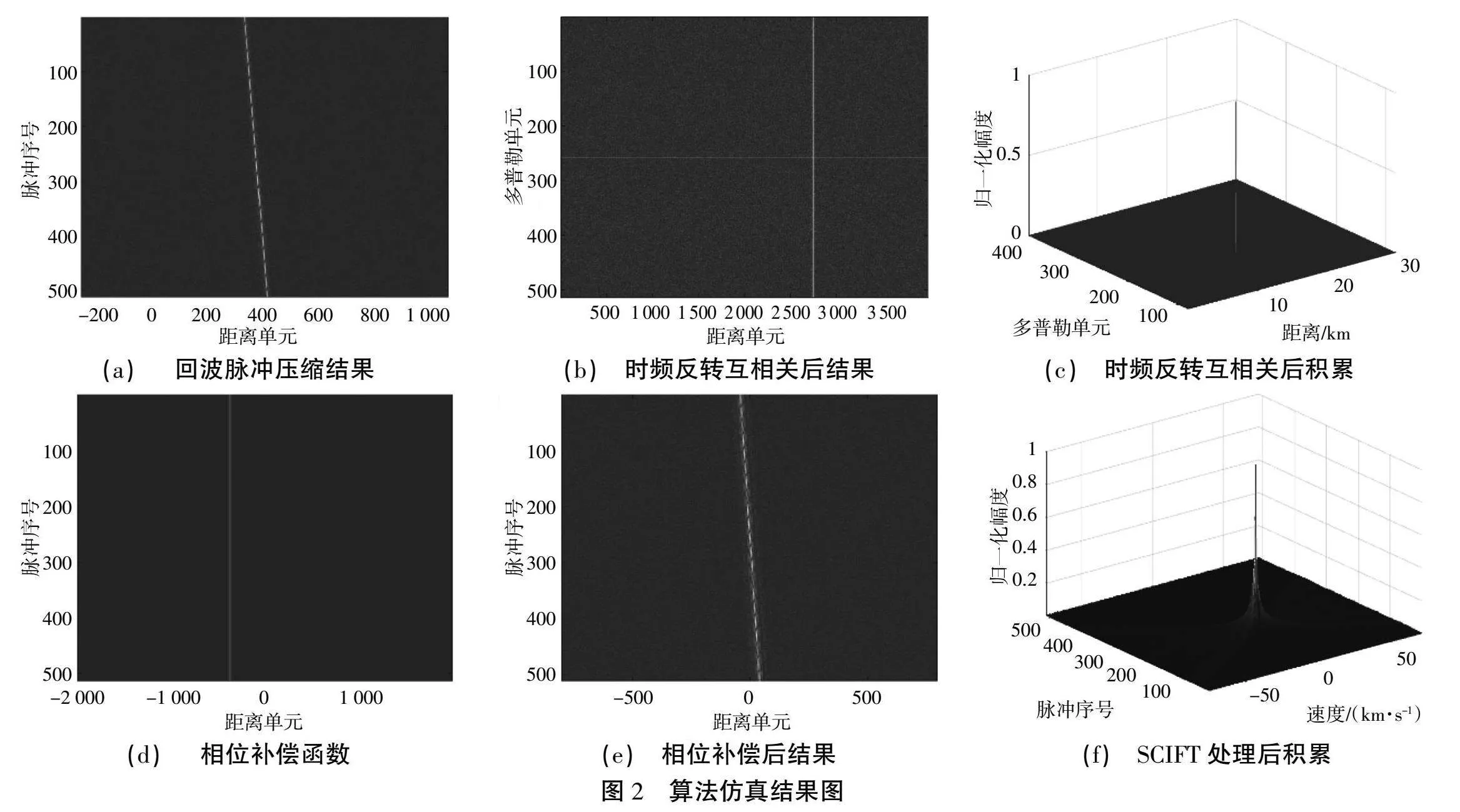
本文算法效果如圖2所示。圖2（a）為單目標回波的脈沖壓縮結果：經過脈沖壓縮的信號包絡峰值隨著慢時間變化。

圖2（b）為目標回波進行時頻反轉互相關后結果：可以觀察到受到跨距離單元走動被成功校正的影響，回波包絡峰值沿一條垂直于距離維的直線分布。

圖2（c）為時頻反轉互相關后通過慢時間FFT進行積累后的結果：通過檢測相干積累峰值坐標，可以計算出目標徑向距離約為13 978 m，與目標真實值相符。

通過時頻反轉互相關得到的徑向距離構造的相位補償函數如圖2（d）所示，在進行了相位補償后的結果如圖2（e）所示：相位補償消除了回波中的距離信息，信號包絡峰值沿著一條過零點的直線分布。

對經過相位補償的信號進行SCIFT解耦合，并沿著慢時間方向FFT進行相干積累，得到的結果如圖2（f）所示：此時相干積累峰值的距離軸坐標只和目標徑向速度有關，通過峰值檢測可以計算得出目標徑向速度約為6 056.2 m/s，與目標真實值相符。

當目標速度滿足8？淄/？濁c≤Ta /2即？淄<Ta ？濁c/16時，不需要考慮目標速度模糊問題。

通過仿真實驗，可以驗證本文提出的算法能夠成功校正高速運動的勻速目標回波中的跨距離單元走動，對發生速度的目標回波，在滿足條件的情況下也能夠順利估算出目標真實的不模糊速度。

4 結論

本文針對高速運動目標雷達探測，提出了一種基于時頻反轉互相關和尺度逆傅里葉變換的相干積累算法，首先利用時頻反轉互相關解決由目標高速度引起的跨距離單元走動問題，并估算出目標徑向距離。在通過徑向距離信息進行相位補償后，采用尺度逆傅里葉變換實現相干積累與目標速度估計。

與其他針對高速機動目標積累算法相比，本文算法不需要參數搜索即可實現目標回波信號能量積累，具備較好的實時性能，可以獲得準確的目標距離和速度信息，具備一定的實用意義。

參考文獻：

[1] FROLUSHKIN V M， NOVOSELTSEV L I . Moving-target detection[J]. Izvestiya Vysshikh Uchebnykh Zavedenij. Radioelektronika，1984，27（7）：11-15.

[2] HUANG P H， LIAO G S， YANG Z W， et al． Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform[J]．IEEE Transactions on Signal Processing，2016，64（15）：4013-4026.

[3] LI Y， ZENG T， LONG T， et al. Range migration compensation and doppler ambiguity resolution by keystone transform[C]//2006 CIE International Comference on Radar，Shanghai，China，2006：1-4.

[4] XU J， YU J， PENG Y， et al. Radon-fourier transform for radar target detection， I： generalized doppler filter bank[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47（2）：1186-1202.

[5] XU J， YU J， PENG Y， et al. Radon-fourier transform for radar target detection （II）： blind speed sidelobe suppression.[J].IEEE Trans. Aerospace and Electronic Systems，2011，47（4）：2473-2489.

[6] YU J， XU J， PENG Y， et al. Radon-fourier transform for radar target detection （III）： optimality and fast implementations.[J].IEEE Trans. Aerospace and Electronic Systems，2012，48（2）：991-1004.

[7] 劉添豪，堯澤昆，陳曦，等.一種空基雷達高速微弱機動目標信號相參積累方法[J].電訊技術，2023，63（9）：1361-1367.

[8] JIBIN Z， TAO S， WENTAO Z， et al. Radar high-speed target detection based on the scaled inverse fourier transform[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2014，8（3）：1-1.