流體的“舞蹈”

當溪水流過大石塊等障礙物時，會被分成兩股交替的、不對稱的旋渦；當風吹過高聳的山峰時，在云層下方會形成一個個旋渦……這些司空見慣的現象背后，其實是流體力學中的卡門渦街原理。

自然界中的神秘圖案

當風吹過山峰、云團，穿過島嶼，都會出現卡門渦街現象，形成自然界中神秘的圖案。

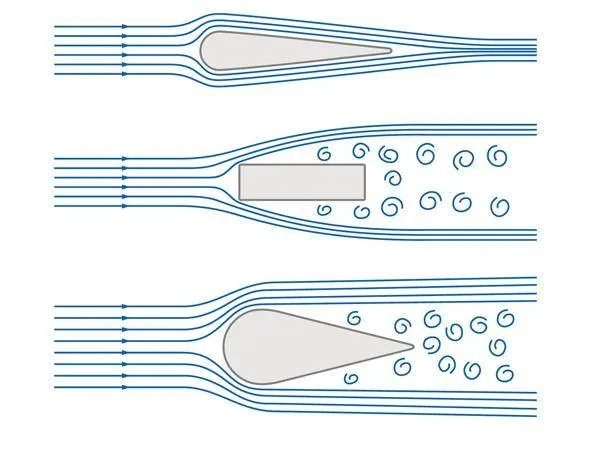
卡門渦街現象是指在一定條件下，氣體或者液體繞過某些物體時，物體兩側會周期性地“脫落”出旋轉方向相反、排列規則的兩列蘑菇狀旋渦，就像在跳舞一樣。

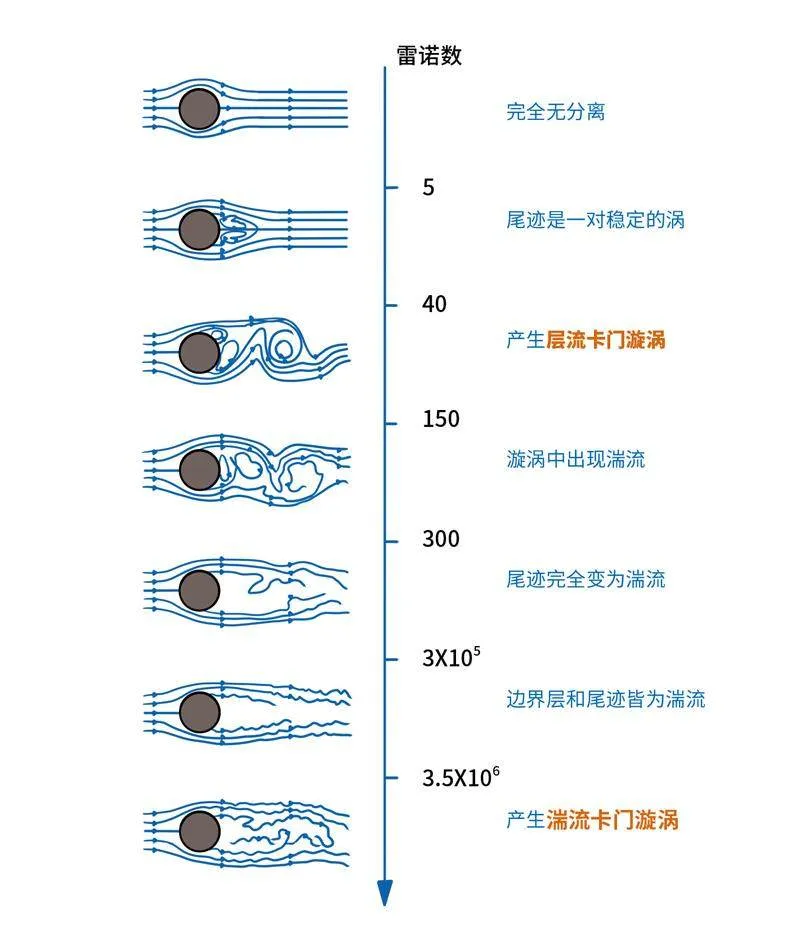
開始時，這兩列蘑菇狀旋渦分別保持自身的運動方向；接著，它們互相干擾、吸引，且干擾越來越大，形成非線性的旋渦；隨著雷諾數（與流體的密度、速度，管道的半徑、流體的黏度有關）的增加，旋渦的形狀會發生一系列變化，形成各種極為復雜的旋渦結構，最后成為湍流。

高懸的電線被風吹過時，會發出嗡鳴聲；汽車在高速行駛時，會受到氣動阻力；潛艇下行時，潛望鏡會產生振動……這些現象都可以用卡門渦街原理解釋。

流體力學的里程碑

在1911～1912年間，德國流體力學家普朗特在觀察水槽中圓柱后方的水流分離現象時發現，水槽里的水流不斷發生擺動。普朗特認為，可能是圓柱表面不夠光滑或水槽做得不對稱。但是，無論如何改進實驗裝置，總是消除不了這種擺動。

馮·卡門（普朗特的學生）抓住了這個令普朗特困惑許久的現象，進行了反復驗證。他觀察到流體流過障礙物時，會形成一排排的小旋渦，而且這些旋渦的脫落頻率和流體的速度有關。馮·卡門將這個現象命名為卡門渦街現象，它標志著流體力學史上又一次重大的發現——不僅揭示了自然界中一個美麗的物理現象，還為工程設計和災害預防提供了重要的理論支持和技術手段。

雷諾數：理解流體流動方式的“工具”

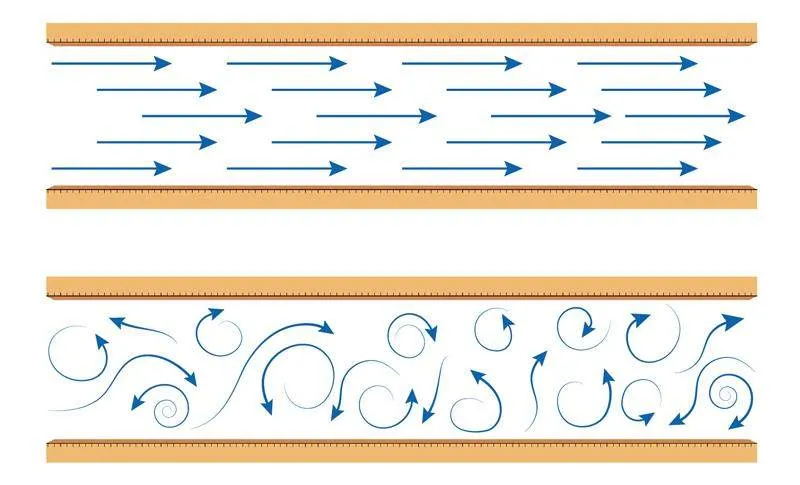
想象一下，當你在水中游泳時，水怎樣流過你的身體？有時，水流得像絲綢一樣平滑；但有時，水流得又亂又急。雷諾數就是幫助科研人員理解流體流動方式的“工具”。

在低雷諾數下，流體流動呈現為有序的層流，各層流體相對獨立地流動，沒有明顯的混合。當雷諾數增加到一定值時，流體流動轉變為湍流，流體層間發生劇烈的混合，流動變得復雜且不可預測。

物體后部是否會出現卡門渦街現象，主要取決于雷諾數，只有當雷諾數處于特定范圍時，才會出現規則的卡門渦街現象。

“雙面利刃”的科學啟示

任何事物的存在都有兩面性，卡門渦街現象展現了自然界和物理學中令人嘆為觀止的奇妙現象，同時也蘊藏著不可忽視的危險。

文明的“加速器”

卡門渦街現象能引發共振——當固體頻率和旋渦頻率接近時，會發生共振，而固體在旋渦作用下產生的振動叫“渦激振動”。

風弦琴就是基于這一原理制造而成的樂器——在木制共鳴箱上安裝幾條琴弦，風吹過琴弦引起振動，就能發出樂聲。這一樂器曾在19世紀的歐洲盛行，多放置于公園、屋頂、古堡等地。

我國古代詩歌中也曾出現過此類樂器，例如唐代詩人高駢所作的《風箏》一詩中寫道：“夜靜弦聲響碧空，宮商信任往來風。依稀似曲才堪聽，又被風吹別調中……”這里的“風箏”是在紙鳶上掛竹笛、能迎風作響的器具，它與風弦琴有著類似構造和發音原理。換言之，中國早在唐朝時期便發現且運用了卡門渦街原理。

科研人員利用卡門渦街現象實現了對風能的捕捉，設計出僅憑一根柱子就可以發電的無葉片風力發電機——空氣流過無葉片風力發電機時，會產生旋渦，誘發柱子產生往復振動從而發電；通過研究卡門渦街現象，工程師設計出渦流發生器等海洋能源設備，利用渦流的動能轉化為電能。

潛藏的“破壞者”

1940年11月7日，位于美國華盛頓州的塔科馬海峽吊橋，在建成僅4個月后就因卡門渦街現象被損毀——當天，風通過橋面下的空間時產生了卡門渦街現象，導致橋面產生劇烈的振動，最終導致橋體結構失效。

再例如，在海上石油生產平臺等海洋工程中，由于卡門渦街現象，海水可能會對石油平臺產生周期性的力，導致其結構受損。

破解之道

為了規避與控制卡門渦街現象帶來的不利影響，科研人員在進行工程設計時，會進行精確的數值分析和嚴格的風洞模型測試。例如，通過微調障礙物的形狀和尺寸，來改變形成卡門渦街現象的條件，從而減少渦流的強度和影響；在關鍵部位安裝阻尼器或振動吸收器，有效吸收因卡門渦街現象引發的振動能量，減少結構的振動幅度；在建筑結構設計中，充分考慮風速、風向等環境因素，采用更加穩固和抗風的設計，減少卡門渦街現象的影響等等。

卡門渦街現象的發現，不僅是流體力學史上的一個里程碑，也是跨學科研究的一個典范。它展示了自然界的奇妙和復雜，同時也提醒我們，科學探索永無止境，每一個現象背后都可能隱藏著更深層次的真理。

（責任編輯 / 高琳 美術編輯 / 周游）