基于最大Lyapunov指數的行星齒輪振動可靠性靈敏度分析



摘要:混沌運動是行星齒輪傳動過程中一種常見的運動狀態,這種運動狀態對齒輪的可靠性和使用壽命有著消極的影響。因此,將齒輪的混沌運動定義為系統的一種失效形式,為齒輪可靠性分析提供了新思路。首先,以行星齒輪傳動系統為研究對象,建立行星齒輪傳動系統的動力學模型。然后,將激勵頻率、剛度波動系數、阻尼系數、溫度作為不確定隨機因素,以最大李雅普諾夫指數(LLE)作為可靠性指標構建極限狀態方程。最后,采用Monte Carlo數值模擬(MCS)的方法求解系統可靠度,并進一步分析了隨機變量均值、標準差對可靠性的敏感程度,為齒輪振動可靠性設計和優化提供了指導建議。
關鍵詞:行星齒輪傳動系統;動力學;最大李雅普諾夫指數;可靠性;靈敏度
中圖分類號:TH132 文獻標志碼:A 文章編號:1671-0797(2024)19-0028-04
DOI:10.19514/j.cnki.cn32-1628/tm.2024.19.007
0 引言
行星齒輪傳動系統因傳動效率高、傳動比大、傳動平穩以及緊湊的結構特性,被廣泛應用于直升飛機主減速器。然而,傳動時非線性因素不可避免,這使得傳動過程中的動態響應變得復雜多變。振動已經成為導致高速齒輪傳動發生破壞失效的一種主要形式,因此,基于齒輪動力學的振動可靠性分析也越發重要。
在工程實際中,由于制造、加工、裝配等誤差、磨損、潤滑、工作環境等因素變化,齒輪傳動系統中充滿諸多不確定性因素,這些因素嚴重影響了齒輪傳動系統的運動特性和可靠性。因此,國內外學者進行了大量研究,孫志禮等人[1]以振動周期內隨機振幅超限為失效準則,基于超越法將動力學與可靠性聯系起來,定義了隨機參數結構系統的振動響應可靠度。Nejad等人[2]基于ISO齒輪設計規范提出了一種長期疲勞損傷評估方法,該方法采用荷載持續時間分布法和兩種動態模型確定風電傳動系統齒輪的可靠性和失效壽命概率。陳川[3]在研究風電齒輪箱傳動系統的可靠性模型時,運用條件概率思想,將激振力頻率與系統固有頻率關聯起來構建可靠性模型,計算了各零部件的振動可靠性,進而建立了串聯系統可靠性模型,并進一步求解了風電齒輪箱傳動系統的振動可靠性。Wang等人[4]建立了單級直齒輪副區間參數動力學模型,研究了嚙合剛度、輸入轉矩、傳動誤差和齒隙等隨機參數對齒輪傳動系統振動速度區間和傳動可靠性的影響。
上述齒輪可靠性分析中,系統的運動狀態鮮被考慮在內。在行星齒輪傳動過程中,由于各種非線性因素的存在,系統的動態響應復雜多變。尤其是復雜的混沌運動,不僅會降低動力傳遞時的穩定性,還會加劇齒輪的磨損,這將導致系統可靠性和使用壽命的降低,甚至引發工程事故。消除或避免齒輪傳動時的混沌運動區間,降低振動噪聲,提高傳動系統平穩性、可靠性和使用壽命,一直是齒輪動力學分析的主要目的[5]。LLE作為衡量動力學特征的一個重要指標,能有效識別系統的運動狀態,這為本文所提出的齒輪振動可靠性模型提供了理論基礎。本文綜合考慮了熱效應、齒側HtjhQZ3SqwFQ/yyJuniPRQ==間隙、時變嚙合剛度、嚙合阻尼、綜合傳動誤差等因素,建立行星齒輪傳動系統的純扭轉非線性動力學模型。充分考慮齒輪傳動系統的運動狀態,將系統的混沌運動定義為失效形式,通過LLE構建行星齒輪振動可靠性模型,將激勵頻率、溫度、時變嚙合剛度、嚙合阻尼視為隨機因素,采用MCS法計算行星齒輪傳動系統的振動可靠度,并進一步分析隨機變量均值和標準差對可靠性的敏感程度,為齒輪振動可靠性設計和優化提供指導建議。
1 行星齒輪非線性動力學模型
1.1 運動微分方程
如圖1所示,行星系統由一個太陽輪s、行星輪pn(n=1,2,3,…,N)、內齒圈r、行星架c組成。令i=spn,rpn,spn和rpn分別表示太陽輪和行星輪、內齒圈和行星輪之間的相互關系,θs、θpn、θr、θc分別為相應部件的扭轉位移。
時變嚙合剛度ki(t)和靜態傳遞誤差ei(t)可由一階諧波Fourier級數表示:
ki(t)=kmi[1+κisin(ωet+φi)],
ei(t)=Eisin(ωet+?i)(1)
式中:kmi為平均嚙合剛度;κi為剛度波動系數;ωe為嚙合頻率;φi為嚙合相位差;Ei為嚙合誤差幅值;?i為初始嚙合誤差相位。
齒輪的嚙合阻尼比可表示為:
ci=2ξi(2)
式中:ξi為阻尼系數;令q=p,g表示主動齒輪和從動齒輪,Mq為等效質量。
采用集中質量建立行星齒輪扭轉動力學模型,系統動力學微分方程為:
Ic
+mpnrc 2
c-
(Fspncos α′ spn)rc,
-
(Frpncos α′ rpn)rc=-Tout,
Ipn
pn+Fspnrbpn-Frpnrbpn=0,
Ir
r+
Frpnrbr=0,
Is
s+
Fspnrbs=Tin(3)
式中:Tin為輸入扭矩;Tout為輸出扭矩;Is、Ipn、Ir、Ic分別為太陽輪、第n個行星輪、齒圈以及行星架的轉動慣量;rc為行星架半徑;rbs、rbpn、rbr分別為太陽輪、第n個行星輪、齒圈的基圓半徑;mpn為行星輪的質量;α′ i為熱變形后的壓力角;Fi為動態嚙合力,Fi=ki(t)f(xi,bi)+
Ci f(i,bi)。
f(xi,bi)為齒輪副的相對位移函數,可表示為:
fi(xi,bi)=xi-bi, xi>bi,
0, |xi|≤bi,
xi+bi, xi<-bi(4)
式中:bi為半齒側間隙。
由于熱效應對齒輪的運動特性有著顯著影響,因此有必要將溫度的影響考慮在內[6]。考慮熱效應半齒側間隙可表示為[7]:
bi=b0-Δbi/2(5)
Δbi=ΔTγ(1+ΔTγ)m[π-(inv α′ i-inv αi)(zp+zg)]+
[mΔTγ(zp+zg)sin αi]/2(6)
式中:b0為固定半齒側間隙;Δbi為由溫度引起的間隙;ΔT為齒輪溫升;γ為齒輪的線性膨脹系數;m為齒輪的模數;αi為壓力角;α′ i為熱變形后的壓力角;zq為齒輪的齒數。
xspn和xrpn分別為太陽輪和內齒圈與第i個行星輪作用線上的相對位移:
xspn=rbsθs+rbpnθpn-rcθccos α′ spn+espn(t),
xrpn=rbrθr-rcθccos α′ rpn-rbpnθpn+erpn(t)(7)
式中:espn(t)為太陽輪和行星輪之間的靜態傳遞誤差函數;erpn(t)為行星輪和內齒圈之間的靜態傳遞誤差函數。
為解決各激勵參數之間數量級相差過大的問題,需對行星齒輪動力學微分方程進行無量綱化處理。引入無量綱時間變量τ和位移標尺bc對動力學模型無量綱化,τ=ωnt,t為時間;固有頻率ωn=,其中,kmspn為太陽輪與行星輪之間的平均嚙合剛度,Ms和Mpn分別為太陽輪和行星輪等效質量。無量綱激勵頻率Ω=ωe/ωn,無量綱齒側間隙bi=bi/bc,無量綱相對位移xi=xi/bc,無量綱速度xi=xi/bcωn,無量綱加速度xi=xi/bcω2 n,無量綱綜合傳遞誤差ei=ei/bc。無量綱化處理后的動力學方程可參考文獻[8]。
1.2 動力學分析
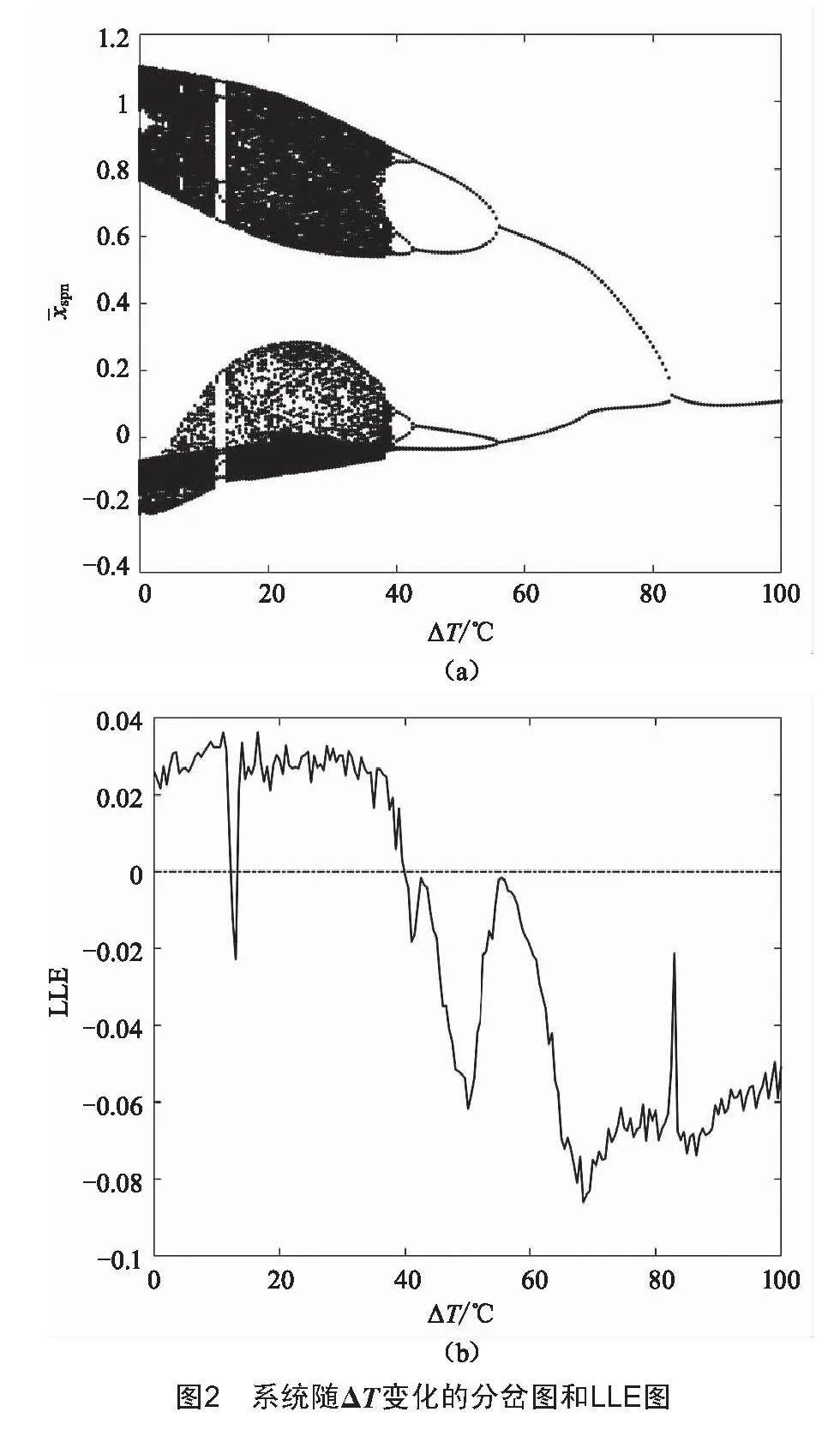
最大李雅普諾夫指數(LLE)是衡量動力學特征的一個重要指標,能有效識別系統的運動狀態[9]。LLE識別系統運動狀態的方法為:當LLE>0時,系統處于混沌狀態;反之,系統則處于周期或擬周期運動狀態。以行星齒輪傳動系統隨ΔT變化的運動特性為例,取系統參數如下:激勵頻率Ω=1,太陽輪和行星輪齒側間隙bspn=4 μm,行星輪和內齒圈的齒側間隙brpn=4 .5μm,阻尼系數ξi=0.1,綜合傳遞誤差幅值Ei=3 μm,剛度波動系數κi=0.25。圖2為系統隨ΔT變化的分岔圖和LLE圖。當ΔT處于[0 ℃,39.5 ℃)區間時,系統以混沌運動狀態為主,并伴隨著短暫的周期運動,此區間的LLE曲線整體大于零并出現小部分區間小于零。當ΔT在[39.5 ℃,100 ℃]時,系統在多處發生逆倍化分岔,由7周期運動→4周期運動→2周期運動→1周期運動,在此區間內LLE的值小于零。可見,LLE可以很好地反映出系統在不同參數下的運動狀態,這為本文所提出的振動可靠性模型提供了理論依據。
2 行星齒輪振動可靠性靈敏度分析
2.1 可靠度定義與靈敏度分析方法
在以往的研究中,Jan N. Fuhg等人研究了結合彈塑性摩擦力模型Duffing型振子的行為,提出將LLE作為非線性模型的可靠性指標,求解系統可靠性[10]。LLE作為非線性動力學的全局分岔分析方法之一,廣泛應用于齒輪動力學分析[11],可作為行星齒輪振動可靠性分析的評價指標。本文采用劉夢軍等人提出的方法求解系統的LLE[12],根據LLE識別系統是否處于混沌運動的判斷方法,系統的極限狀態函數可定義為:
Z(x)=-LEE(x)>0, 安全,
-LEE(x)≤0, 失效(8)
式中:LEE(x)表示輸入隨機變量x時對應的LLE值。
采用Monte Carlo方法近似計算失效概率:
Pf=IF[Z(x)](9)
式中:NMC為總樣本;IF(·)為失效域指數函數,IF(·)=1表示行星齒輪系統振動失效,IF(·)=0表示行星齒輪系統可靠。
通常表示為:
IF[Z(x)]=1, Z(x)≤0,
0, Z(x)>0(10)
對于統計獨立的隨機變量,可靠性靈敏度表示為失效概率Pf對基本隨機變量xi的分布參數θ (k)(包含均值μ和標準差σ)的偏導[13]:
=dx=E
(11)
式中:Xi為第i個隨機變量;θ (k)為分布參數,k表示分布參數的個數;fX(x)為隨機變量xi的概率密度函數;E(·)為期望算子。
可靠性靈敏度的估計值?f/?θ (k)為:
=
(12)
式中:N為總樣本數;xj為第j個樣本;IF(xj)為極限狀態函數。
無量綱處理后的均值μ和標準差σ的靈敏度可表示為:
Sμ=×=IF(xi)×(13)
Sσ=×=×(14)
2.2 可靠性靈敏度分析
本文以某型直升機主減速器的行星齒輪系統為研究對象,行星齒輪個數為3,系統的基本參數如表1所示。
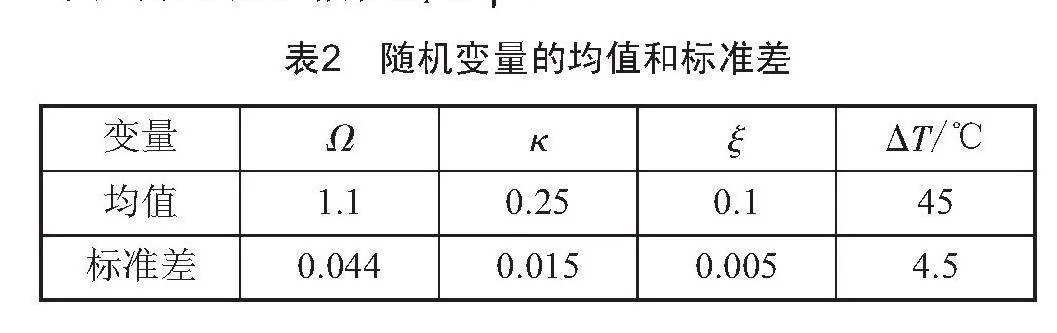
行星齒輪長時間工作將導致溫度的升高,當溫度升高時,齒側間隙也會隨之減小,也從側面反映了間隙對系統振動特性的影響,但在對齒輪可靠性分析當中卻很少考慮此因素。因此,本文將激勵頻率Ω、剛度波動系數κi、阻尼系數ξi、溫度ΔT視為隨機參數,且符合正態分布,采用經驗法選取變異系數,均值和標準差如表2所示。給定齒側間隙bsp=4 μm,brp=4.5 μm,綜合傳遞誤差幅值Ei=3 μm。
本文設計變量有4個,總樣本NMC=8×104,采用MCS對系統可靠性求解,所求得的失效概率為Pf=7.125×
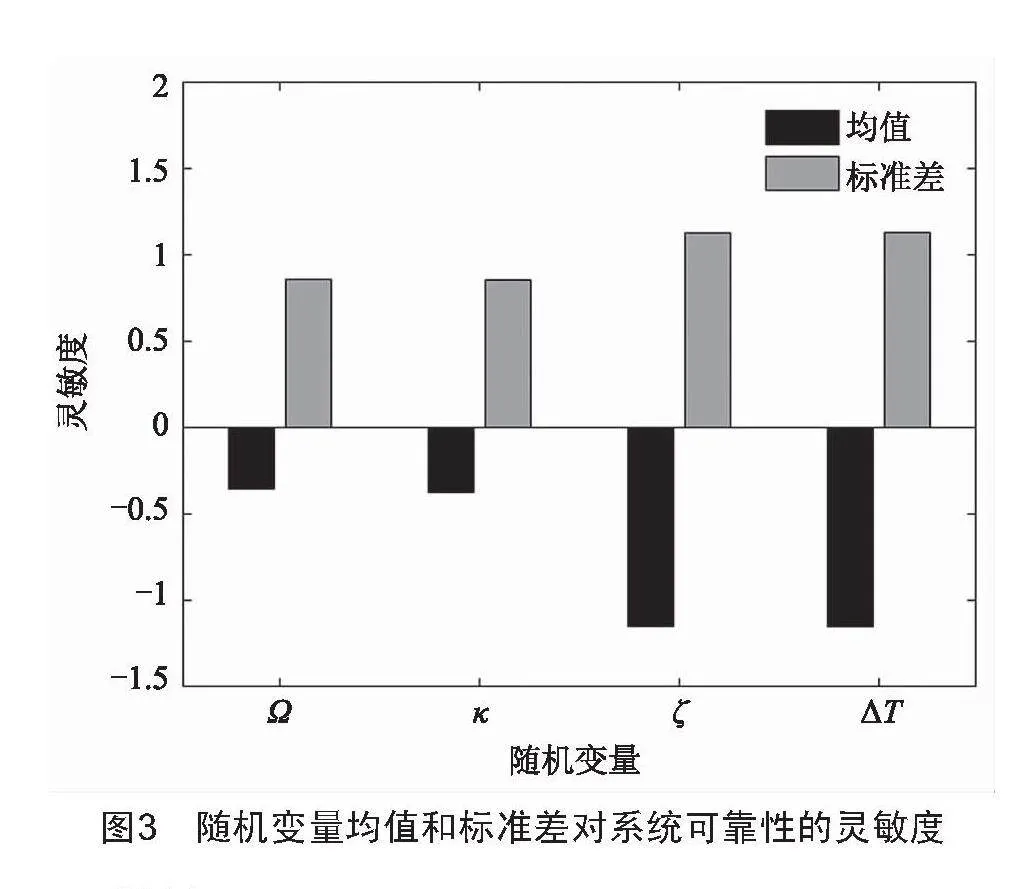
10-3。由圖3可得,這4個隨機變量的均值對系統的可靠性有著積極的影響,這說明隨著隨機變量均值的增加,系統的可靠性也在增加,其中ΔT的影響程度最大,ξ次之,隨后是κ和Ω。而隨機變量的標準差均對系統的可靠性有著消極的影響,隨著隨機變量標準差的增大,系統可靠性會降低,且各隨機變量標準差的影響程度先后排序與均值相同。綜上分析,建議在齒輪振動可靠性設計中重點關注阻尼系數和溫度以及與溫度相關的齒側間隙,嚴格控制其精度。
3 結論
1)本文基于行星齒輪傳動系統的動力學模型,將混沌運動視為系統的失效形式,以LLE作為可靠性指標構建極限狀態函數,為行星齒輪振動可靠性分析提供了一種新的方法。
2)溫度和阻尼系數的均值和標準差對系統的可靠性影響程度較大,在進行行星齒輪系統振動可靠性設計和優化時應重點考慮溫度(溫度與齒側間隙的關系)和阻尼系數對系統可靠性的影響,嚴格控制其精度。
[參考文獻]
[1] 孫志禮,袁哲.齒輪隨機參數系統非線性振動響應可靠性分析[J].東北大學學報(自然科學版),2011,32(6):838-842.
[2] NEJAD A R,GAO Z,MOAN T.On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains[J].International Journal of Fatigue,2014,61:116-128.
[3] 陳川.風電齒輪箱傳動系統振動及可靠性分析[D].蘭州:蘭州理工大學,2016.
[4] WANG J,ZHANG J.Effects of random interval parameters on spur gear vibration[J].Journal of Vibration and Control,2021,27(19/20):2332-2344.
[5] SHENG L C,LI W,WANG Y Q,et al.Nonlinear dynamic analysis and chaos control of multi-freedom semi-direct gear drive system in coal cutters[J].Mechanical Systems and Signal Processing,2019,116:62-77.
[6] GOU X F,ZHU L Y,QI C J.Nonlinear dynamic model of a gear-rotor-bearing system considering the flash temperature[J].Journal of Sound and Vibration,2017,410:187-208.
[7] LIU H,YAN P F,GAO P.Effects of temperature on the time-varying mesh stiffness,vibration response,and support force of a multi-stage planetary gear[J].Journal of Vibration and Acoustics,2020, 142(5):051110.
[8] 劉寧.考慮非光滑因素的行星齒輪傳動系統非線性動力學研究[D].沈陽:沈陽理工大學,2020.
[9] KOCAREV L,SZCZEPANSKI J,AMIGó J M,et al.Discrete chaos-i:Theory[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2006,53(6):1300-1309.
[10] FUHG J N,AMéLIE FAU.Surrogate model approach for investigating the stability of a friction-
induced oscillator of Duffing's type[J].Nonlinear Dynamics,2019,98(5):1709-1729.
[11] 劉夢軍,沈允文,董海軍.單級齒輪非線性系統吸引子的數值特性研究[J].機械工程學報,2003(10):111-116.
[12] WANG J Y,LIU N,WANG H T,et al.Analysis of nonlinear dynamic characteristic of a planetary gear system considering tooth surface friction[J].Proceedings of the Institution of Mechanical Engineers,Part J:Journal of Engineering Tribology,2021,235(11):2376-2395.
[13] 孫安邦.齒輪傳動系統非線性動力學與可靠性研究[D].沈陽:東北大學,2015.
收稿日期:2024-05-27
作者簡介:崔燦(1999—),男,山東濟寧人,碩士,研究方向:齒輪動力學及可靠性。

