高中物理繩桿中的運動分解問題探究

【摘要】在高中物理教學(xué)中，繩桿中的運動分解問題是一個重要的內(nèi)容.本文通過對繩桿運動分解問題的探討，旨在幫助學(xué)生更好地理解運動的合成與分解，提高學(xué)生解決問題的能力.通過實例分析，展示繩桿運動分解問題在實際問題中的應(yīng)用.

【關(guān)鍵詞】高中物理；繩桿運動；解題技巧

1 引言

繩桿運動分解是基于運動的合成與分解原理.在繩桿運動中，通過將物體的運動分解為沿繩桿方向和垂直于繩桿方向的兩個分運動，可以將繩桿運動問題分解為兩個獨立的分運動問題，分別求解后再進(jìn)行合成.通過運用運動的合成與分解原理，學(xué)生可以將復(fù)雜的繩桿運動問題分解為簡單的分運動，從而簡化問題并求解.

2 繩桿中運動分解問題概述

例1 如圖1所示，在小船靠岸模型中，輕繩通過定滑輪連接小船，繩端速度為v，方向水平，當(dāng)船連接的輕繩與水平面的夾角為α?xí)r，求小船的運動速度.

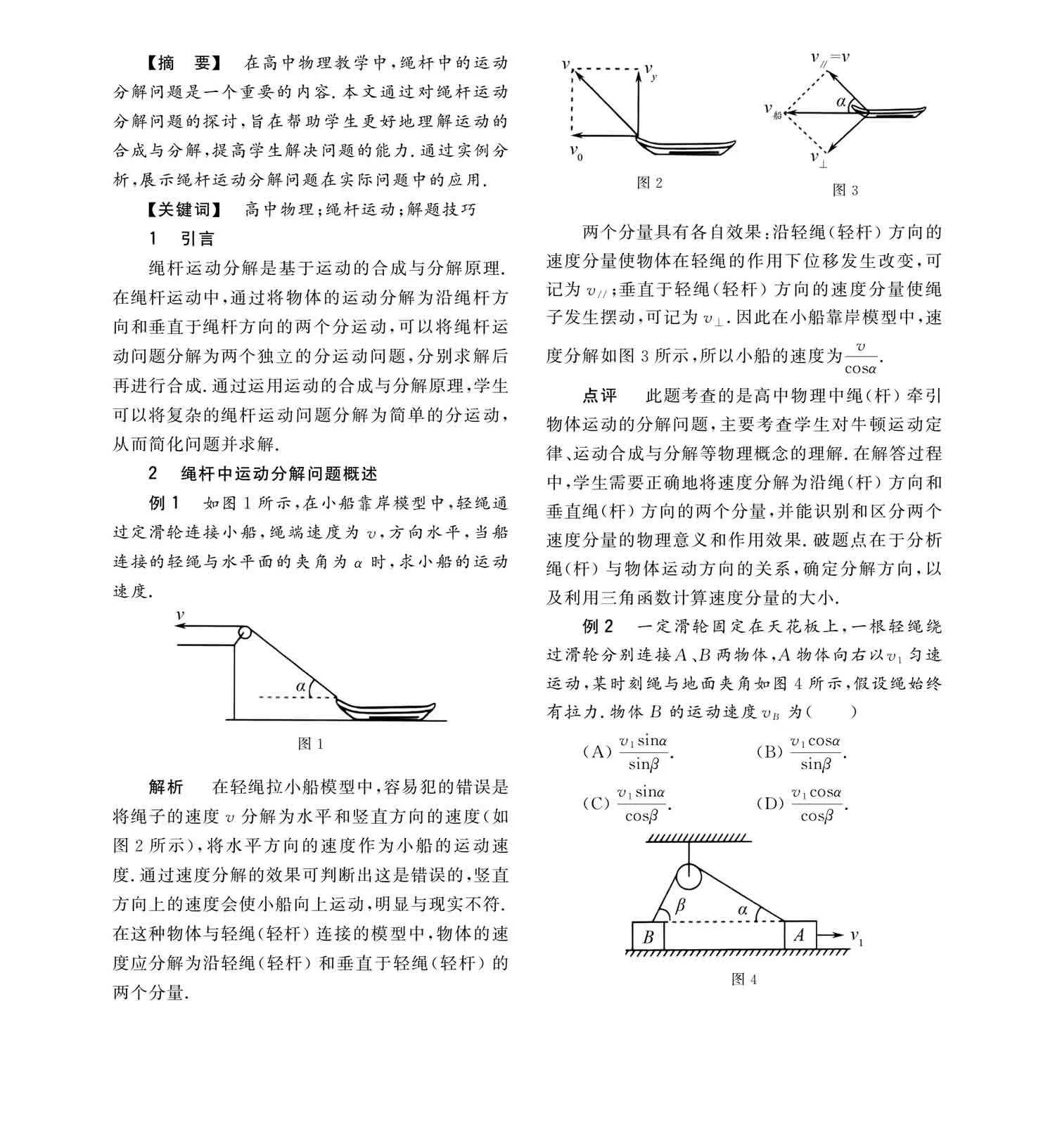
解析 在輕繩拉小船模型中，容易犯的錯誤是將繩子的速度v分解為水平和豎直方向的速度（如圖2所示），將水平方向的速度作為小船的運動速度.通過速度分解的效果可判斷出這是錯誤的，豎直方向上的速度會使小船向上運動，明顯與現(xiàn)實不符.在這種物體與輕繩（輕桿）連接的模型中，物體的速度應(yīng)分解為沿輕繩（輕桿）和垂直于輕繩（輕桿）的兩個分量.

兩個分量具有各自效果：沿輕繩（輕桿）方向的速度分量使物體在輕繩的作用下位移發(fā)生改變，可記為v//；垂直于輕繩（輕桿）方向的速度分量使繩子發(fā)生擺動，可記為v⊥.因此在小船靠岸模型中，速度分解如圖3所示，所以小船的速度為vcosα.

點評 此題考查的是高中物理中繩（桿）牽引物體運動的分解問題，主要考查學(xué)生對牛頓運動定律、運動合成與分解等物理概念的理解．在解答過程中，學(xué)生需要正確地將速度分解為沿繩（桿）方向和垂直繩（桿）方向的兩個分量，并能識別和區(qū)分兩個速度分量的物理意義和作用效果．破題點在于分析繩（桿）與物體運動方向的關(guān)系，確定分解方向，以及利用三角函數(shù)計算速度分量的大小．

例2 一定滑輪固定在天花板上，一根輕繩繞過滑輪分別連接A、B兩物體，A物體向右以v1勻速運動，某時刻繩與地面夾角如圖4所示，假設(shè)繩始終有拉力.物體B的運動速度vB為（ ）

（A）v1sinαsinβ. （B）v1cosαsinβ.

（C）v1sinαcosβ. （D）v1cosαcosβ.

解析 如圖5、圖6所示，將A和B的速度分解為沿輕繩和垂直于輕繩方向，因為輕繩長度不發(fā)生變化，故沿著輕繩方向速度相等，所以vBcosβ=v1cosα，解得vB=v1cosαcosβ，故（D）正確.

點評 本題考查學(xué)會對物體進(jìn)行運動的分解，涉及平行四邊形定則與三角函數(shù)知識，同時本題的突破口是沿著繩子的方向速度大小相等．在解答過程中，學(xué)生仍然需要正確地將速度分解為沿繩方向和垂直繩方向的兩個分量，并利用滑輪系統(tǒng)中繩子各點速度相等的特性，不能直接將繩子的速度等同于物體的速度，特別是在有角度的情況下，要注意區(qū)分沿繩方向和垂直繩方向的速度分量對物體運動的不同影響，并在實際問題中考慮重力、摩擦力等其他可能影響物體運動的因素．

例3 光滑地面和豎直墻面呈垂直狀態(tài)，小明將長直輕桿AB靠在墻面，某時刻松手，輕桿開始滑動，當(dāng)輕桿滑動至如圖7所示狀態(tài)時，輕桿與墻面夾角為θ，A端速度大小為v1，B端速度大小為v2，則v1，v2的關(guān)系是（ ）

（A）v1=v2. （B）v1=v2cosθ.

（C）v1=v2tanθ. （D）v1=v2sinθ.

解析 如圖8所示，將A端和B端速度分解為沿輕桿和垂直于輕桿的速度分量，因為沿桿方向速度相等，所以v1cosθ=v2sinθ，解得v1=v2tanθ，故（C）正確.

點評 本題雖不同于前兩例，但解題本質(zhì)依然是速度的正確分解，解決本題的關(guān)鍵是將A、B兩點的速度分解為沿桿子方向和垂直于桿的方向，以及知道沿桿方向上的兩個分速度大小相等．

3 結(jié)語

本文通過對繩桿運動分解問題的探討，介紹了繩桿運動分解的原理和技巧解法的應(yīng)用.通過實例分析，展示了繩桿運動分解問題在實際問題中的應(yīng)用.掌握繩桿運動分解的方法對于理解和解決高中物理中的相關(guān)問題具有重要意義.

參考文獻(xiàn)：

［1］江明隆.高中物理運動體系分解的經(jīng)驗方法［J］.當(dāng)代旅游（高爾夫旅行），2018（07）：181.

［2］鄭南軒.關(guān)于運動分解的一些要點闡述［J］.中外企業(yè)家，2018（15）：106.

［3］李昱龍.高中物理中的運動分解法［J］.農(nóng)家參謀，2017（19）：87.