巧用圖象法求一元二次方程的近似根
【摘要】一元二次方程在數學中占據了重要的地位,是初中數學的重要內容.對于求解一元二次方程,通常使用公式法或配方法.然而,有時候這些方法可能不適用,或者需要大量的計算.在這種情況下,可以嘗試用圖象法求出一元二次方程的近似根.本文介紹如何巧用圖象法求一元二次方程的近似根.
【關鍵詞】初中數學;圖象法;一元二次方程
用圖象法求解一元二次方程的近似根,是快速處理數學問題的方法之一.根據一元二次方程寫出對應的函數表達式,在平面直角坐標系中畫出函數圖象,根據函數圖象,找到根的可能位置,觀察根附近的函數值,確定根的近似值.
1探索規律找解法
例1方程2x2+x-2=0的近似根可以看作是下列哪兩個函數圖象交點的橫坐標()
(A)y=2x2和y=x-2.
(B)y=2x2+x和y=2.
(C)y=2x2-2和y=x.
(D)y=-2x2和y=x+2.
解析由2x2+x-2=0得2x2=-x+2,則方程可看作函數y=2x2和y=-x+2的圖象的交點,故(A)錯誤;由2x2+x-2=0得2x2+x=2,則方程可看作函數y=2x2+x和y=2的圖象的交點,故(B)正確;由2x2+x-2=0得2x2-2=-x,則方程可看作函數y=2x2-2和y=-x的圖象的交點,故(C)錯誤;由2x2+x-2=0得-2x2=x-2,則方程可看作函數y=-2x2和y=x-2的圖象的交點,故(D)錯誤.
點評本題考查了一元二次方程與二次函數的關系,正確變形是關鍵.通過本例可以看出,一元二次方程的近似根可通過作函數圖象的方法求解.
2在解題中深化解法
例2小朋在學習過程中遇到一個函數y=12xx-32.
(1)當x≥0時,y與x的幾組對應值如表1,結合表1,畫出當x≥0時,函數y=12xx-32的圖象;
(2)若關于x的方程12xx-32=kx-1有一個實數根為2,則該方程其他的實數根約為(結果保留小數點后一位).
解析(1)根據列表,描點連線,如圖1.
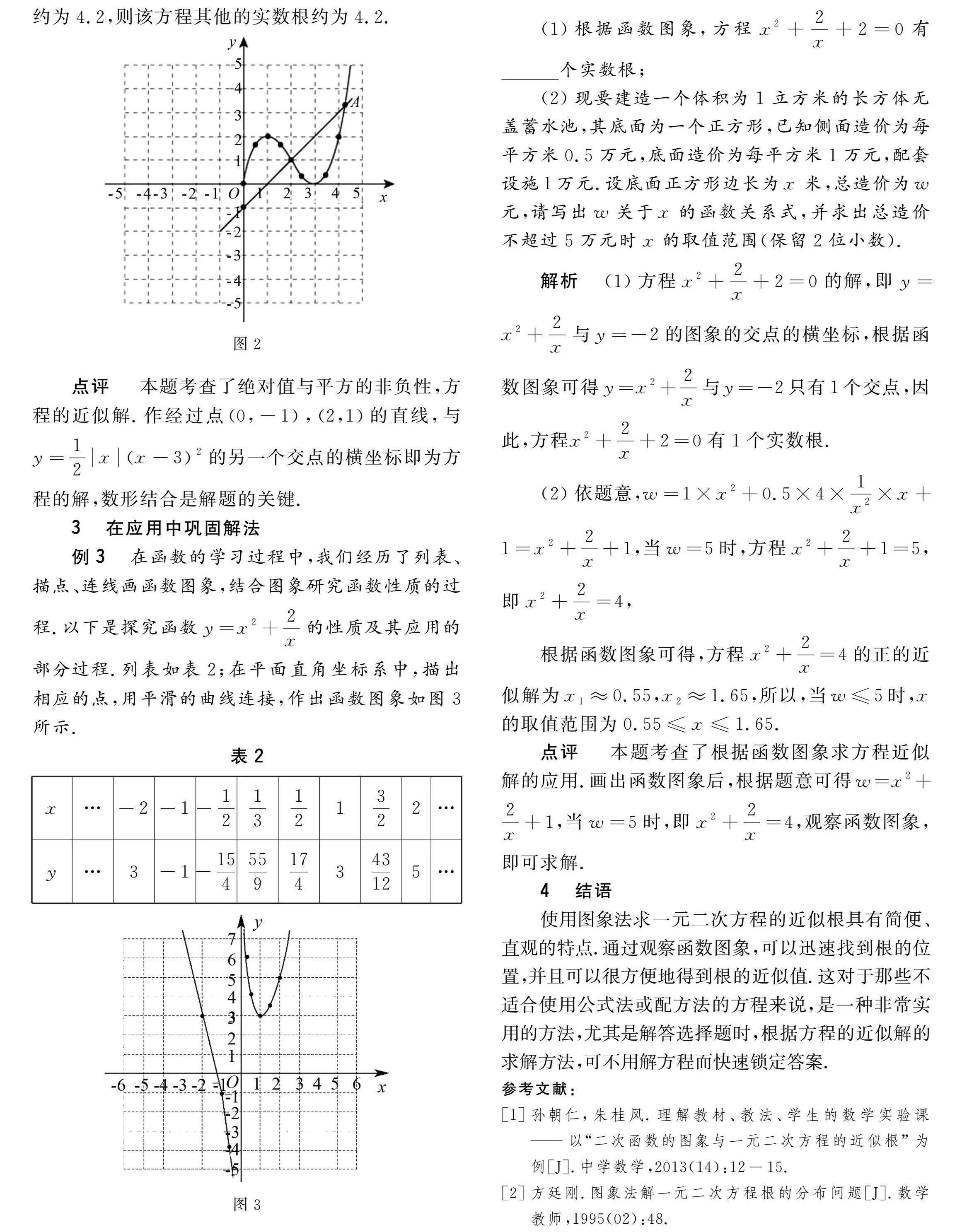
(2)依題意,12xx-32=kx-1有一個實數根為2,則過點2,1,12xx-32=kx-1的解即為y=12xx-32與y=kx-1的交點的橫坐標,且y=kx-1過點0,-1,如圖2,作過點0,-1,2,1的直線,與y=12xx-32交于點A,根據函數圖象的交點可知點A的橫坐標約為4.2,則該方程其他的實數根約為4.2.
點評本題考查了絕對值與平方的非負性,方程的近似解.作經過點0,-1,2,1的直線,與y=12xx-32的另一個交點的橫坐標即為方程的解,數形結合是解題的關鍵.
3在應用中鞏固解法
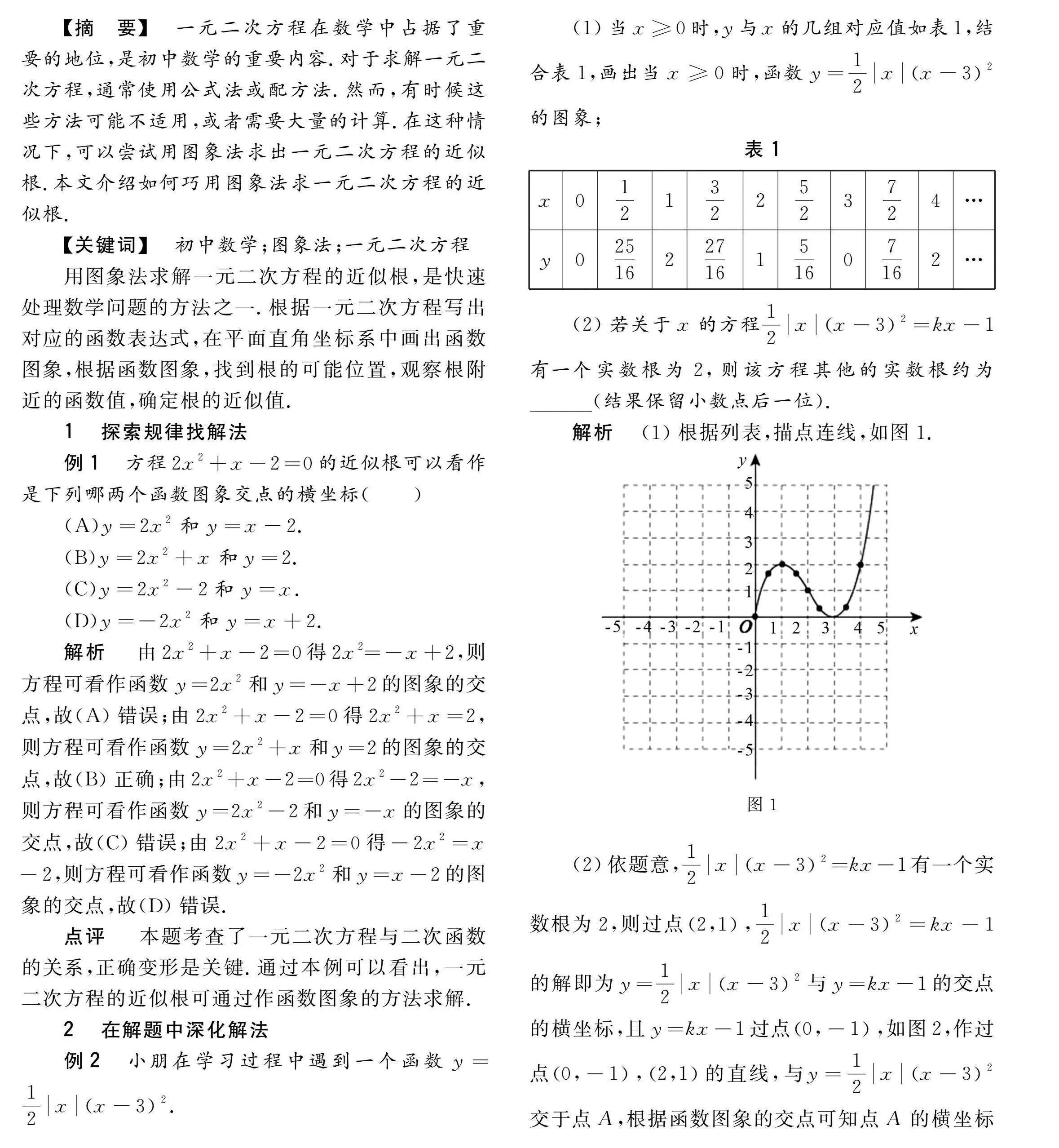
例3在函數的學習過程中,我們經歷了列表、描點、連線畫函數圖象,結合圖象研究函數性質的過程.以下是探究函數y=x2+2x的性質及其應用的部分過程.列表如表2;在平面直角坐標系中,描出相應的點,用平滑的曲線連接,作出函數圖象如圖3所示.
(1)根據函數圖象,方程x2+2x+2=0有個實數根;
(2)現要建造一個體積為1立方米的長方體無蓋蓄水池,其底面為一個正方形,已知側面造價為每平方米0.5萬元,底面造價為每平方米1萬元,配套設施1萬元.設底面正方形邊長為x 米,總造價為w元,請寫出w關于x的函數關系式,并求出總造價不超過5萬元時x的取值范圍(保留2位小數).
解析(1)方程x2+2x+2=0的解,即y=x2+2x與y=-2的圖象的交點的橫坐標,根據函數圖象可得y=x2+2x與y=-2只有1個交點,因此,方程x2+2x+2=0有1個實數根.
(2)依題意,w=1×x2+0.5×4×1x2×x+1=x2+2x+1,當w=5時,方程x2+2x+1=5,即x2+2x=4,
根據函數圖象可得,方程x2+2x=4的正的近似解為x1≈0.55,x2≈1.65,所以,當w≤5時,x的取值范圍為0.55≤x≤1.65.
點評本題考查了根據函數圖象求方程近似解的應用.畫出函數圖象后,根據題意可得w=x2+2x+1,當w=5時,即x2+2x=4,觀察函數圖象,即可求解.
4結語
使用圖象法求一元二次方程的近似根具有簡便、直觀的特點.通過觀察函數圖象,可以迅速找到根的位置,并且可以很方便地得到根的近似值.這對于那些不適合使用公式法或配方法的方程來說,是一種非常實用的方法,尤其是解答選擇題時,根據方程的近似解的求解方法,可不用解方程而快速鎖定答案.
參考文獻:
[1]孫朝仁,朱桂鳳.理解教材、教法、學生的數學實驗課——以“二次函數的圖象與一元二次方程的近似根”為例[J].中學數學,2013(14):12-15.
[2]方廷剛.圖象法解一元二次方程根的分布問題[J].數學教師,1995(02):48.

