初中數學函數應用題的解題方法探究

【摘要】在初中數學教學體系中，函數知識占據著核心地位，也是中考數學試卷的必考內容.但是多數初中學生認為函數知識過于抽象，學習難度、理解難度比較高，難以準確掌握函數解題方法，同時也容易出現抵觸情緒，每當學生看到函數應用題型時，便出現消極思想，使學生的解題效率大打折扣.本文對初中數學函數應用題的解題方法進行分析，希望為初中數學教師教學提供新思路.

【關鍵詞】初中數學；函數應用；解題方法

函數相關知識是初中數學教學的主要內容，也是中考數學中的常見題型.為此，初中數學教師要注重應用題解題教學環節，為學生打下堅實的函數知識學習基礎，向學生傳授有效的解題方法，強化學生的數學思維能力，使學生真正掌握函數的解題要點，提高學生的問題解決能力.

1完善知識體系，確立問題要求

在初中函數應用題解題教學中，教師要注重解題思路、解題方法的傳授，幫助學生建立完整的知識體系，確立問題要求，分析問題中的有效條件，使學生理解題意內容.在滬科版初中數學教材中，函數知識以一次函數、反比例函數、二次函數為主，而二次函數也是歷屆中考的重要考點，占據較高的分值.為了提高學生的函數應用題解題能力，教師在解題教學時，需要幫助學生理清知識題型，增強學生的讀題能力，使學生能夠準確掌握問題的題干與題眼[1]，明確自己所要解決的問題，從而使學生在解題時保持數學思路清晰，提高學生的解題效率.同時，初中數學教師還要根據中考改革相關要求，讓學生明確問題所要考查的知識點，依照函數解析式，找到相應的特殊點，通過圖象特點，對問題中的隱藏條件進行分析，以此找到解決問題的關鍵點.

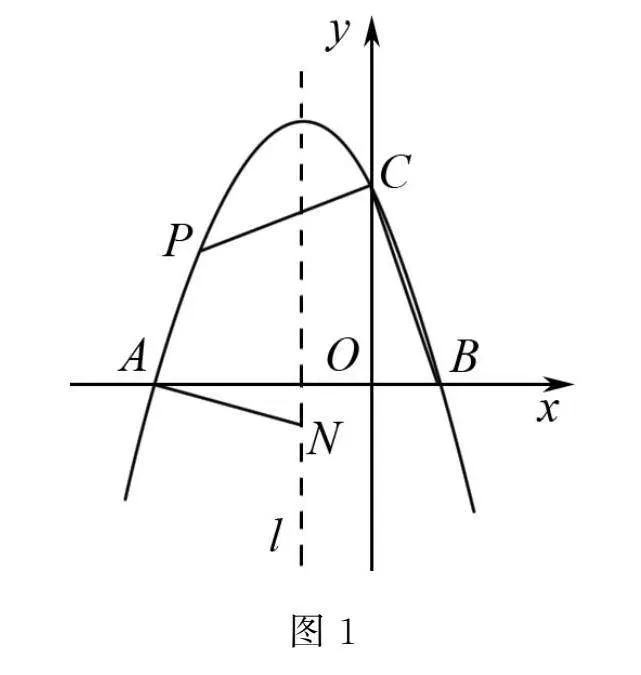
例1如圖1所示，已知拋物線y=ax2+bx+c與x軸有兩個交點，即點A、點B，其中點B的坐標為（2，0），和y軸有一個交點，即點C（0，6），對稱軸l為x=-2.

（1）求拋物線函數解析式.

（2）有一動點N，處于對稱軸l上，在第二象限的拋物線中，有一動點P，若PA=NA且PA⊥NA，求此時P點

的坐標.四邊形PABC面積最大時，求四邊形PABC面積最大值以及此時點P的坐標是多少？

解析對于二次函數應用題，教師要引導學生轉變固有思維認知，把抽象復雜的問題進行簡化，使學生能夠完全理解題目.對于該問題，教師可指導學生把點的坐標當成線段長度，再將線段長度變成自己熟知的方程式，便能將求證面積最大值問題變成底邊最大值問題，降低學生的解題難度.如此一來，學生便能理清自己的解題思緒，準確得出相應的答案.

2注重解題細節，培養類比思想

在初中函數應用題解題教學中，教師要注重細節的把控，培養學生的類比思想，提高學生的解題效率.類比思想主要指在解題時，讓學生回顧與這一問題相似的題目，找尋二者的關聯性，通過類型模擬當時的解題方法，找到解決問題的關鍵點，使問題迎刃而解.類比思想也被稱為“變式訓練”[2]，可使學生達到融會貫通、學以致用的效果，但是想要讓學生熟練掌握這一方法，教師還要讓學生注重問題思考環節，找到解決問題的關鍵點，明確函數自變量取值界限等知識，不能盲目照搬照抄，否則容易影響最終的解題正確率.

例2籃球運動員投籃后球的運動路線類似于拋物線，若該拋物線的對稱軸設定為直線x=2.5，求：（1）籃球運動路線的函數表達式以及自

變量的取值范圍.（2）在籃球運動時，籃球距地面的最遠距離.

解析對于此類問題，教師可帶領學生共同回顧之前所做的題目，學生發現這一問題和運動員推鉛球問題具有相似性，從而拿出自己的數學筆記，回想教師講解運動員推鉛球問題的解題思路，并注意問題細節的分析，依照現有的問題條件，畫出與之相符合的圖示，找到相應的未知數量，梳理數量內在關系，分析籃球運動的拋物線.

3實現轉換思維，強化學科思維

初中學生在面對函數應用問題時，常常因解題思路模糊，陷入惡性循環.這樣不但浪費了學生寶貴的學習時間，還會打消學生的學習信心.為此，初中數學教師在函數應用題解題教學時，要注重發揮自身的引導作用，讓學生學會轉換思維，促進數量之間的相互轉換，學生基于逆向思維進行問題思考，把相應的已知條件假設為已知數，把變量當成產量，降低學生的解題難度，進而提高學生的解題效率，強化學生的逆向思維能力.

例3已知x1和x2是關于x的方程（x-2）（x-m）=（t-2）（t-m）的兩個實數根，（1）求x1和x2的值.（2）如若將x1和x2當成直角三角形的兩個直角邊，當m和t滿足什么條件，才能保證這一直角三角形面積最大？這一三角形面積的最大值是多少？

解析初中數學教師輔導學生解決這一函數應用題時，如若直接對實數m與t進行分析，學生能夠發現無法得出答案，不但浪費做題時間，還會使學生陷入惡性循環，影響學生的解題實效.教師可讓學生通過反思推導的方式，把問題中的m實數、t變量假設成常量，并將其常量x計算出來，以便梳理x、m（實數）、t的關系，得出相應答案.如此一來，學生將原方程進行變式：x2-（m+2）x+2m=t2-（m+2）t+2m，由于x2-t2-（m+2）x+（m+2）t=0，所以（x-t）（x+t）-（m+2）（x-t）=0，也就是（x-t）（x+t-m-2）=0，得出x1=t，x2=m+2-t.在解答第二問時，學生可根據直角三角形的面積公式，列出12x1x2=12t（m+2－t），計算得出在t=m+22，且保證m＞-2的情況下，以x1與x2為直角邊的直角三角形面積最大，最大面積為（m+2）28或者12t2.

4結語

綜上所述，在初中數學教學中，函數知識占據著主導地位，也是中考必考題型之一.由于函數知識涉及眾多內容，解題難度比較大，教師要根據中考改革變化要求，運用行之有效的教學方法，指導學生找準數量關系，分析問題中的隱藏條件，理清學生的解題思路，才能使學生的問題解決能力進一步提升.

參考文獻：

[1]曾文玲.初中數學應用題教學中數學建模法的應用[J].教學管理與教育研究，2023（22）：81-84.

[2]楊周，榮麟.以探究活動為支點，撬動課堂數學建模——以“銳角三角函數的簡單應用”教學為例[J].中學數學（初中版），2022（03）：7-8+18.