二次函數與幾何綜合題常見最值問題分析


【摘要】 初中階段,二次函數與幾何綜合題中,最值問題一直是考查的熱點,一般出現在壓軸題目中.這類問題是對學生函數、幾何圖象等知識的綜合考查,其難度較大,在中考中,學生的得分效果并不理想,嚴重影響了學生的成績.本文結合實際問題,對常見題型及其解題方法進行總結.
【關鍵詞】二次函數;初中數學;最值
在數學領域,二次函數與幾何圖形的結合常常產生一系列富有挑戰性的問題,其中最值問題尤為突出.這類問題不僅要求學生熟練掌握二次函數的性質,還需要學生靈活運用幾何知識.通過深入分析這些問題,可以發現,求解最值的關鍵往往在于如何準確找到二次函數與幾何圖形之間的內在聯系,以及如何巧妙運用數學工具進行求解.
1 周長最值
周長問題與線段最值問題有著異曲同工之妙,這類問題主要依托二次函數,考查一些特殊圖形周長的計算.在涉及周長的最值問題中,通常會存在兩條邊是變化的,其余邊長均為固定值,因此在解題中便可以將圖象周長轉化為兩邊最值問題.在此基礎之上,便可以通過作對稱點的方法,將兩條邊轉化在一條線段上,而后求解最大值或最小值.
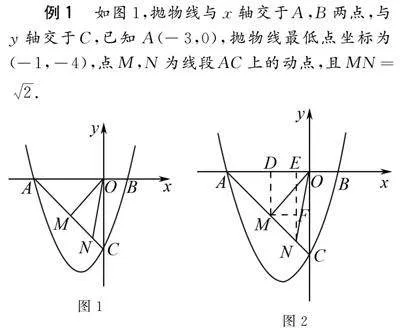
例1 如圖1,拋物線與x軸交于A,B兩點,與y軸交于C,已知A(-3,0),拋物線最低點坐標為(-1,-4),點M,N為線段AC上的動點,且MN=2.
(1)求拋物線解析式;
(2)求△OMN周長的最小值.
解析 (1)因為拋物線最低點坐標為(-1,-4),
所以設拋物線表達式為y=a(x+1)2-4,
將A(-3,0)代入得4a-4=0,則a=1,
則拋物線表達式為y=x2+2x-3.
(2)令x2+2x-3=0,
解得x1=-3,x2=1,
則A(-3,0),C(0,-3),
易得直線AC的方程為y=-x-3,
設M(t,-t-3)且(-3<t<-1)
如圖2,過點M,N分別向x軸作垂線,垂足分別為D,E,過點M向EN作垂線,垂足為F,則EF∥y軸.
因為OA=OC,
則∠OAC=45°,∠FMN=45°,
因為MN=2,
則MF=FN=1,
則N(t+1,-t-4),
則OM+ON=(t-0)2+(-t-3)2+
[t-(-1)]2+(-t-4)2,
其表示點(t,-t)到點P(0,3)和點Q(-1,4)的距離之和,
其中點(t,-t)在y=-x上,由最短距離模型可知OM+ON最短為QP′,
其中點P′為點P關于y=-x的對稱點,
易得P′(-3,0),
則QP′=[-1-(-3)]2+42=25,
則△OMN周長的最小值為25+2.
2 面積的最值問題
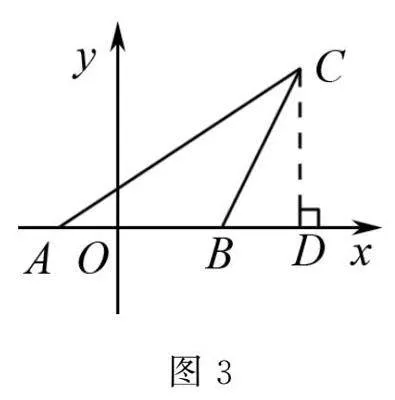
在二次函數面積最值問題中,會涉及三角形、四邊形等圖象,在解題中,通常將其轉化為三角形間的關系進行求解.在三角形面積最值中,當三角形有一條邊在坐標軸上時,通常以坐標軸所在邊為底,過頂點作底邊垂線,頂點的橫坐標或縱坐標的絕對值則為三角形的高.如圖3,AB在x軸上,此時C點的縱坐標則為三角形的高CD,進而得出面積表達式進行解題.
當三角形沒在坐標軸上時,可以通過輔助線將三角形面積轉化為其他三角形面積的和或差.在四邊形面積中,同樣通常轉化為兩個三角形的面積之和,通過分別求解三角形面積,進而解答實際問題.需要注意的是,在轉化過程中,應當盡可能轉化為計算較為簡單的三角形面積之和,以降低計算難度.
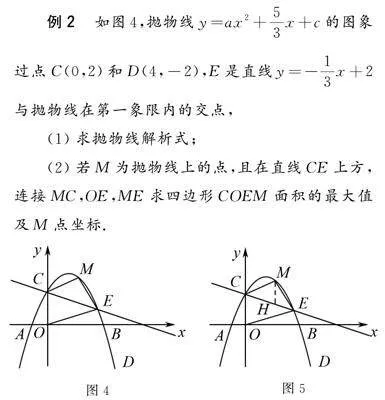
例2 如圖4,拋物線y=ax2+53x+c的圖象過點C(0,2)和D(4,-2),E是直線y=-13x+2與拋物線在第一象限內的交點,
(1)求拋物線解析式;
(2)若M為拋物線上的點,且在直線CE上方,連接MC,OE,ME求四邊形COEM面積的最大值及M點坐標.
解析 (1)拋物線經過點C(0,2),D(4,-2),
代入y=ax2+53x+c,
可得a=-23,c=2,
則y=-23x2+53x+2.
(2)如圖5,過點M作y軸平行線交CE于點H,
設M(m,-23m2+53m+2),
則H(m,-13m+2),
所以MH=(-23m2+53m+2)-(-13m+2)=
-23m2+2m,
聯立y=-23x2+53x+2和y=-13x+2,
可得E點坐標為(3,1),C點坐標為(0,2),
所以S四邊形COEM=S△CEO+S△CME=12×2×3+12MH×3
=-m2+3m+3=-(m-32)2+214,
故當m=32時,S四邊形COEM有最大值214,此時M點坐標為(32,3).
3 結語
綜上所述,二次函數與幾何圖象綜合題是中考中常見的壓軸題,其中最值問題則是常見的考查點之一.通過上述例題可以發現,相關問題并沒有特別復雜,理清思路后,便可以快速解題.
參考文獻:
[1]陳國玉.分類例析基于二次函數的最大值問題[J].初中數學教與學,2023(11):35-37.
[2]謝陳.二次函數中的線段最值問題[J].數理天地(初中版),2022(23):26-27+30.
[3]吳燕.關于初中二次函數面積最值問題的研究[J].數理天地(初中版),2023(13):4-5.

