探究定值,多解歸一

【摘要】幾何定值問題是中考數學中的一類基本問題,涵蓋了線段、三角形、四邊形等多種幾何元素,同時還對相似和全等三角形、勾股定理等知識綜合考查.本文結合一道實例探討幾何定值問題的多種解法,在不同視角下尋求共同的解題規律,幫助學生攻克難點,培養其邏輯思維能力和幾何想象能力,提高數學學科核心素養.
【關鍵詞】初中數學;幾何定值;一題多解
1 例題呈現
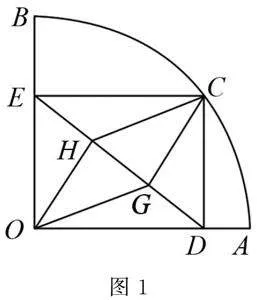
如圖1所示,已知扇形AOB的半徑OA=3,∠AOB=90°,點C是弧AB上異于A,B的動點,過點C作CD⊥OA于點D,作CE⊥OB于點E,連接DE,G,H兩點在線段DE上,且DG=GH=HE,求證:CD2+3CH2為定值.
2 問題分析
對題目進行簡單分析后,可以得到以下基本結論:
結論1 四邊形OECD是矩形,且ED=OC=3.四邊形OGCH是平行四邊形.
結論2 由于H,G兩點是線段ED的三等分點,因此可以構造出相似比為1∶3或2∶3的相似三角形.
結論3 四邊形OECD是矩形,可以利用矩形的直角性質,結合勾股定理解題.
3 視角展示
視角1 添加平行線構造成比例線段,結合相似三角形和勾股定理解題.
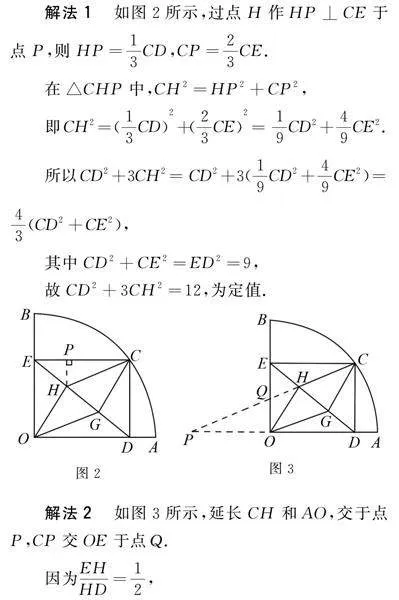
解法1 如圖2所示,過點H作HP⊥CE于點P,
則HP=13CD,CP=23CE.
在△CHP中,CH2=HP2+CP2,
即CH2=(13CD)2+(23CE)2
=19CD2+49CE2.
所以CD2+3CH2=CD2+3(19CD2+49CE2)=43(CD2+CE2),
其中CD2+CE2=ED2=9,
故CD2+3CH2=12,為定值.
解法2 如圖3所示,延長CH和AO,交于點P,CP交OE于點Q.
因為EHHD=12,
所以CP=3CH,PO=DO,
則CP2=9CH2=PD2+CD2.
因為PD2=4OD2=4(OC2-CD2),
所以9CH2=4(OC2-CD2)+CD2.
又因為OC=3,
所以9CH2=36-3CD2,
故CD2+3CH2=12.
評注 觀察發現CD與CH并非在特殊三角形中,進一步分析,“G,H兩點在線段DE上,且DG=GH=HE”是平行線等分線段定理的明顯特征條件,所以考慮從不同的方向作平行線,從而構造成比例線段,利用相似三角形的性質解題.
視角2 利用已有平行線構造相似三角形,結合比例關系解題.
解法3 如圖4所示,延長OG,交CD于點P.
可得△EOG∽△DPG,
所以CD=2PD,OG=23OP.
所以CD2+3CH2=CD2+3(23OP)2=CD2+43OP2
=CD2+43(PD2+OD2)=CD2+43(14CD2+OD2)=12.
評注 由于矩形的對邊平行,平行線間的“對頂三角形”一定相似,因此可以考慮利用“兩條直線被一組平行線所截,所得的對應線段成比例”的基本事實解題.
視角3 構造雙直角模型,利用射影定理解題.
解法4 如圖5所示,過點C作CM⊥ED于點M.
在Rt△CED中,CM⊥ED,
由射影定理可知CD2=MD·DE=3MD.
所以CD2+3CH2=CD2+3(CM2+HM2)=CD2+3(CD2-MD2+HM2)
=CD2+3CD2+3(HM+MD)(HM-MD)=4CD2+3HD(HD-2MD)
=12MD+6(2-2MD)=12.
評注 雙直角模型與射影定理聯系緊密,可以構造出線段的比例關系,同時還可以根據直角利用勾股定理列出等式.
視角4 建立坐標系,用解析法解題.
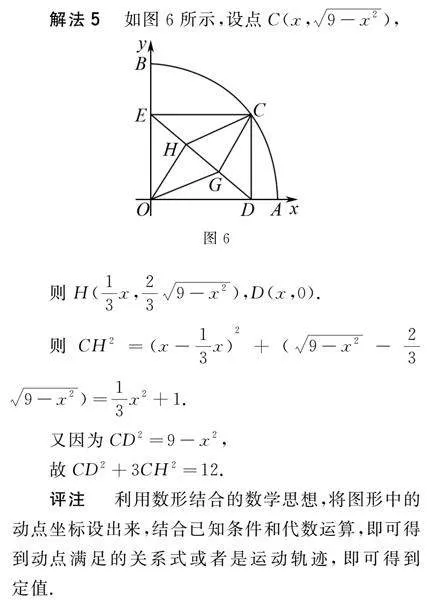
解法5 如圖6所示,設點C(x,9-x2),
則H(13x,239-x2),D(x,0).
則CH2=(x-13x)2+(9-x2-239-x2)=13x2+1.
又因為CD2=9-x2,
故CD2+3CH2=12.
評注 利用數形結合的數學思想,將圖形中的動點坐標設出來,結合已知條件和代數運算,即可得到動點滿足的關系式或者是運動軌跡,即可得到定值.
4 結語
經過對這道中考幾何定值問題的深入探討,不難發現,此類問題雖然看似復雜,思路難以開展,但是只要我們掌握了基本的幾何定理和解題技巧,問題就能迎刃而解.在平時的解題訓練中,要注重觀察圖形的特點,嘗試從不同的角度提出解題方案,同時還要積極利用數形結合思想來簡化解題.

