一道線段長度問題的解題方法研究

【摘要】 線段長度問題是平面幾何問題中的常見問題,涉及知識點多樣,考查學生對于數(shù)形結(jié)合思想、化歸轉(zhuǎn)化思想等數(shù)學思想的理解程度.本文探究一道線段長度問題的解題思路,通過詳細分析題目特點,提出多種解題方法,并對每一種方法作出評注.通過對不同方法的分析,歸納解題規(guī)律,以求進一步完善線段長度問題的理論體系.
【關鍵詞】線段長度;解題技巧;初中數(shù)學
例題呈現(xiàn)
如圖1所示,已知AC為圓O的直徑,B為圓上(除點A、C外一點),∠ABC的角平分線交圓O于點D.若AB=6,BC=2,求BD的長.
方法展示
視角1 建立線段等式
解法1 解三角形
三角形是平面幾何問題中的基本圖形,利用解三角形的處理方法,結(jié)合三角函數(shù)的知識即可解題.
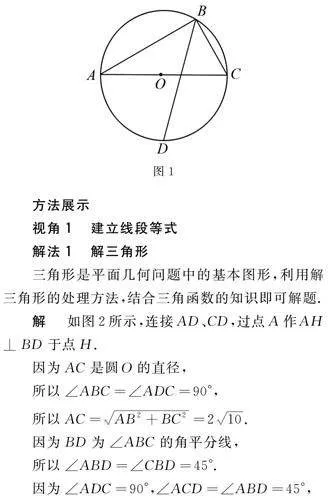
解 如圖2所示,連接AD、CD,過點A作AH⊥BD于點H.
因為AC是圓O的直徑,
所以∠ABC=∠ADC=90°,
所以AC=AB2+BC2=210.
因為BD為∠ABC的角平分線,
所以∠ABD=∠CBD=45°.
因為∠ADC=90°,∠ACD=∠ABD=45°,
所以AD=CD=AC·sin45°=25,
所以AH=BH=AB·sin45°=32.
所以DH=AD2-AH2=2,
BD=BH+DH=42.
解法2 利用面積的不變性
等面積法是解答許多平面幾何問題的重要方法,利用面積的不變性可以得到邊長之間
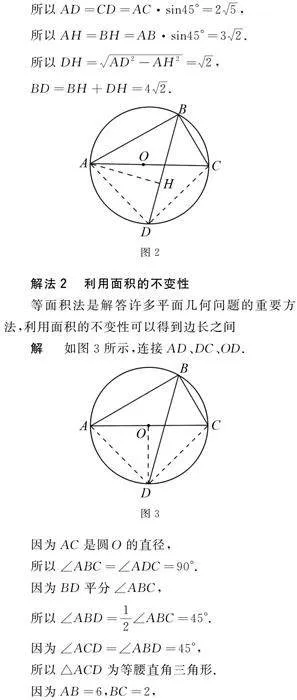
解 如圖3所示,連接AD、DC、OD.
因為AC是圓O的直徑,
所以∠ABC=∠ADC=90°.
因為BD平分∠ABC,
所以∠ABD=12∠ABC=45°.
因為∠ACD=∠ABD=45°,
所以△ACD為等腰直角三角形.
因為AB=6,BC=2,
所以AD=CD=25.
因為S四邊形ABCD=AB·BC2+AD·DC2=BD·ABsin45°2+BD·BCsin45°2,
所以BD=42.
評注 本題是一個靜態(tài)幾何問題,在解決平面幾何問題中的基本思路中,首先要考慮根據(jù)幾何圖形的結(jié)構(gòu)特征建立方程求解,將幾何問題代數(shù)化.解三角形、利用面積的不變性等都是對線段建立等式的常用方法.
視角2 利用圖形變化
解法3 相似變化
解 如圖4所示,過點E作EF∥BC,交AB于點F,連接CD.
因為EF∥BC,所以△AEF∽△ACB.
因為AC是圓O的直徑,所以∠AFE=∠ABC=90°.
因為BD為∠ABC的角平分線,所以∠ABE=∠CBE=45°,EF=FB.
因為AB=6,BC=2,所以AFFE=ABCB=3,EF=32,BE=322.
因為∠BAE=∠BDC,∠ABE=∠DBC,所以△ABE∽△DBC,ABBD=BEBC,BD=42.
解法4 軸對稱變化
解 如圖5所示,連接AD、CD.在BA上截取線段BM,使得BM=BC,連接DM,并過點D作DN⊥AB于點N.
因為AC是圓O的直徑,
所以∠ABC=∠ADC=90°.
因為AB=6,BC=2,所以AC=210.
因為BD平分∠ABC,所以∠ACD=∠ABD=∠CBD=45°,AD=CD=25.
因為BM=BC,BD=BD,∠ABD=∠CBD,所以△BMD≌△BCD.
所以BM=BC=2,DM=CD=25.
所以MN=12AM=2,BN=BM+MN=4.
在Rt△DNM中,DN=DM2-MN2=4,
在Rt△DNB中,BD=DN2+BN2=42.
評注 圖形變化在初中平面幾何問題中具有重要的作用,主要的圖形變化方式有相似變化、軸對稱變化、旋轉(zhuǎn)變化等等.圖形變化的目的是將結(jié)合條件進行位置上的聚焦,從而便于幾何量的求解.
結(jié)語
通過對上述這道典型例題兩個視角的分析,可以發(fā)現(xiàn),對于靜態(tài)的幾何問題主要可以從兩個方面來解決:一是利用平面幾何的相關性質(zhì)和定理建立關于幾何量的等式,二則是善于使用各種圖形變換,擺脫原本的圖形結(jié)構(gòu),將已知條件進行位置上的轉(zhuǎn)化,從而得到相應的答案.

