初中數學圖象題中的“動點問題”解題步驟探究



【摘要】在當前的初中數學教學中,圖象題尤其是動點問題,由于其獨特的解題思路和技巧,往往成為學生學習的難點.本文以初中數學圖象題中的動點問題為研究對象,旨在探討其解題步驟.通過具體例題,詳細講解動點問題的解題步驟,探討在解題過程中可能遇到的一些困難和挑戰,以及如何克服這些困難,從而幫助學生在面對動點問題時,能夠有一個清晰的解題思路,提高解題的準確性和效率.
【關鍵詞】動點問題;初中數學;解題方法
1 引言
在初中數學教學過程中,動點問題作為圖象題的重要組成部分,一直以來都是學生學習的重點和難點.本文將從動點問題的解題思路出發,并通過具體例題,詳細講解解題步驟.同時,還將探討如何運用這些解題步驟,解決實際問題,從而提高學生的數學思維能力和解題技巧.
2 試題呈現
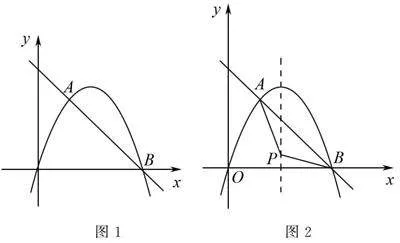
如圖1,在平面直角坐標系xOy中,已知二次函數y=ax2+bxa≠0的圖象經過點A2,4,與x軸交于點B6,0,一次函數y=kx+nk≠0的圖象經過A,B兩點.
(1)求二次函數和一次函數的函數表達式;
(2)若點P是二次函數圖象對稱軸上的點,且PA=PB,如圖2,求點P的坐標;
(3)點M是二次函數圖象位于第一象限部分上的一動點,過點M作x軸的垂線交直線AB于點N,若點M的橫坐標為m.試探究:是否存在常數m,使得MN的長為4?若存在,求出m的值,若不存在,請說明理由.
3 思路分析
圖象題(不僅僅是動點問題)第一問往往是求函數解析式,這時候把已知條件中的坐標代入,求未知量即可.因此第(1)問中,只需要把點A、B的坐標代入拋物線和直線表達式,即可求解.涉及距離問題,必須掌握的是坐標系中兩點之間的距離公式,這對解決動點問題非常重要.第(2)問中,P為定點,難度較低,只需要先求出二次函數的對稱軸,設P3,t,再用兩點間距離公式列方程即可求解.第(3)問是動點問題中經典的求“距離或長度”的問題,該類問題的解題思路一般為:①將動點坐標設為未知量;②用距離公式和坐標,表示出含未知量的距離表達式;③根據未知量的取值范圍,求解長度的取值范圍;④在長度取值范圍中篩選滿足條件的具體值.因此該問可以先設點M的坐標為m,-12m2+3m,且0<m<6,再根據MN的長為4列出方程-12m2+3m--m+6=4求解即可.
4 解法探究
(1)利用待定系數法,把點A2,4,B6,0代入拋物線y=ax2+bxa≠0,
得4a+2b=436a+6b=0,
解得a=-12b=3,
故二次函數的表達式為:y=-12x2+3x;
把A2,4,B6,0代入一次函數表達式y=kx+nk≠0,
得2k+n=46k+n=0,
解得k=-1n=6,
故一次函數的表達式為:y=-x+6;
(2)二次函數y=-12x2+3x的對稱軸為直線x=-32×-12=3,
由點P是二次函數圖象對稱軸上的點,可設P3,t,這樣的設定可以用未知量t來表示待求點的坐標,從而簡化問題.然后將待求點坐標根據已知條件構建含參等式,求解未知量即可.步驟如下:
因為PA=PB(已知條件),
所以PA2=PB2(等式雛形),
所以(3-2)2+(t-4)2=(3-6)2+t2(含參等式),
解得:t=1,
所以P3,1;
(3)在前兩問的基礎上,易想到該題需要根據點的坐標和已知條件來構建含參等式.至此已經知道二次函數和一次函數的具體形式,可以通過將點M、N的坐標代入二次函數和一次函數的方程中,得到兩個關于m的坐標.然后就可以通過構建方程來求出m的值,從而得到待求點的坐標.
因為第一象限點M的橫坐標為m.
所以點M坐標為m,-12m2+3m(0<m<6),
所以點N坐標為m,-m+6,
因為MN的長為4,
所以-12m2+3m--m+6=4,
所以-12m2+4m-6=4 ①,
或-12m2+4m-6=-4 ②,
解方程①,無解;
解方程②有m1=4-23,m2=4+23(舍去),
所以m的值為4-23.
5 結語
本題是二次函數的綜合題,熟練掌握二次函數的圖象及性質,兩點間距離公式是解題的關鍵,在最后一步中,通過m的取值范圍進行得數的舍去,是非常重要的難點,也是“討論思維”的重點.解決圖象動點問題的關鍵在于將待求點的坐標用未知量表示,然后根據坐標和已知條件構建含參等式,最后求解未知量即可.這種方法不僅適用于本文中二次函數的圖象題,也適用于其他類型的圖象題.通過掌握這種方法,學生可以提高解決動點問題的能力,提高數學思維和解題技巧.通過本文的探究,學生深入了解了初中數學圖象題中的動點問題的解題步驟.從問題的解題思路,再到具體的解題步驟,筆者都進行了詳細的闡述和講解,主要強調了理解動點問題的關鍵在于理解點的運動規律,以及如何運用這些規律解決問題.
參考文獻:
[1]潘竹樹,李祎.借助數學抽象 培養關鍵能力——以“數軸上的動點問題”為例[J].數學通報,2023,62(08):34-38+47.
[2]駱建新.初中數學最值問題的突破途徑[J].教育科學論壇,2022(25):72-74.
[3]陳壇椿,邵為爽.數學核心素養觀下的動點問題教學研究[J].高師理科學刊,2020,40(06):69-72.

