初中數(shù)學(xué)四邊形問題中對(duì)角互補(bǔ)模型的理解和應(yīng)用



【摘要】隨著我國(guó)教育改革的深入推進(jìn),培養(yǎng)學(xué)生的邏輯思維和解決問題的能力成為教育的重要目標(biāo)之一.本文主要探討初中數(shù)學(xué)四邊形問題中對(duì)角互補(bǔ)模型的理解和應(yīng)用,通過具體的例子和問題,展示如何利用對(duì)角互補(bǔ)模型推導(dǎo)四邊形的性質(zhì)和定理.
【關(guān)鍵詞】初中數(shù)學(xué);對(duì)角互補(bǔ)模型;解題技巧
1 引言
在初中數(shù)學(xué)四邊形問題中,對(duì)角互補(bǔ)模型是一個(gè)重要的概念.對(duì)角互補(bǔ)模型在解決四邊形問題中起著關(guān)鍵的作用.通過利用對(duì)角互補(bǔ)模型,我們可以推導(dǎo)出四邊形的各種性質(zhì)和定理.很多情況下對(duì)角互補(bǔ)模型的理解和應(yīng)用是解決四邊形問題的關(guān)鍵,掌握了這個(gè)模型,學(xué)生可以更好地理解和解決四邊形問題.本文以一道對(duì)角互補(bǔ)模型的例題,展示對(duì)角互補(bǔ)模型在四邊形解題中的重要性.
2 試題呈現(xiàn)
例1 在四邊形ABCD中,∠B+∠D=180°,對(duì)角線AC平分∠BAD.
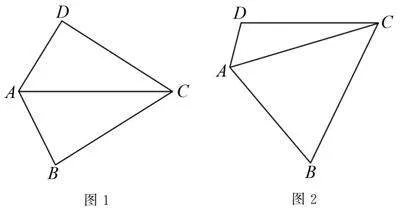
(1)如圖1,若∠DAB=120°,且∠B=90°,試探究邊AD,AB與對(duì)角線AC的數(shù)量關(guān)系為.
(2)如圖2,若將(1)中的條件“∠B=90°”去掉,(1)中的結(jié)論是否成立?請(qǐng)說明理由.
(3)如圖3,若∠DAB=90°,若AD=3,AB=7,求線段AC的長(zhǎng)和四邊形ABCD的面積.
3 思路分析
(1)先證Rt△DAC≌Rt△BAC,得出AD=AB,再求∠DCA的度數(shù),得出AD=12AC,進(jìn)而求出AD+AB=AC.
(2)先畫輔助線:以C為頂點(diǎn),AC為一邊作∠ACE=60°,∠ACE的另一邊交AB延長(zhǎng)線于點(diǎn)E,作輔助線后證明△ACE為等邊三角形,根據(jù)四邊形內(nèi)角和為360°,∠B+∠D=180°,求出∠DCB=60°,進(jìn)而證明△CAD≌△CEB,得出AD=BE,最后得出AD+AB=AC.
(3)先證△ACE為等腰直角三角形,再證明△ADC≌△EBC,得出AD=BE,進(jìn)而求出AC=52,求四邊形ABCD的面積可以轉(zhuǎn)化為求△ACE的面積.
4 解法探究
(1)因?yàn)椤螧+∠D=180°,∠B=90°,
所以∠D=∠B=90°.
因?yàn)閷?duì)角線AC平分∠BAD,
所以∠DAC=∠BAC.
因?yàn)锳C=AC,
所以Rt△DAC≌Rt△BACAAS,
所以AD=AB.
因?yàn)椤螪AB=120°,
所以∠DAC=12∠DAB=60°,
所以∠DCA=30°,
所以AD=12AC,
所以AD=AB=12AC,
所以AD+AB=AC.
(2)問題(1)中結(jié)論成立,理由如下:
以C為頂點(diǎn),AC為一邊作∠ACE=60°,∠ACE的另一邊交AB延長(zhǎng)線于點(diǎn)E,如圖4所示.
由(1)可得:∠CAB=60°,
則因?yàn)椤螦CE=60°,
所以∠AEC=60°,
所以△ACE為等邊三角形,
所以AC=AE=CE.
因?yàn)椤螪+∠ABC=180°,
∠CBE+∠ABC=180°,
所以∠D=∠CBE;
因?yàn)椤螦BC+∠D+∠DAC+∠DCB=360°,
∠D+∠ABC=180°,∠DAB=120°,
所以∠DCB=60°,
所以∠DCB=∠ACE,
所以∠DCB-∠ACB=∠ACE-∠ACB,
所以∠DCA=∠BCB,
所以△CAD≌△CEBAAS,
所以AD=BE.
因?yàn)锳C=AE=AB+BE,
所以AC=AD+AB.
(3)過點(diǎn)C作CE⊥AC交AB延長(zhǎng)線于點(diǎn)E,如圖5所示.
因?yàn)閷?duì)角線AC平分∠BAD,∠BAD=90°,
所以∠CAE=∠DAC=45°.
因?yàn)镃E⊥AC,
所以∠ACE=90°,
所以∠E=180°-∠ACE-∠CAE=45°,
所以∠E=∠CAE,∠E=∠DAC,
所以AC=CE;
因?yàn)椤螦BC+∠D=180°,
∠ABC+∠CBE=180°,
所以∠D=∠CBE,
所以△ADC≌△EBCAAS,
所以AD=BE,
所以AE=AB+BE=AB+AD;
因?yàn)锳D=3,AB=7,
所以AE=10;
在Rt△ACE中,AC2+CE2=AE2,
所以AC=CE=52,
所以S△ACE=12×52×52=25;
因?yàn)椤鰽DC≌△EBC,
所以S△ADC=S△EBC,
所以S四邊形ABCD=S△ADC+S△ACB=S△EBC+S△ACB=SACE=25.
5 結(jié)語
在四邊形中,邊和角的特殊性可能會(huì)帶來一些隱含的性質(zhì),本題中的“對(duì)角互補(bǔ)”特殊性,帶來了隱含“邊的性質(zhì)”.在四邊形的幾何世界中,每條邊和每個(gè)角都扮演著獨(dú)特的角色,它們的特殊性不僅是它們自身的屬性,更是整個(gè)四邊形性質(zhì)的關(guān)鍵.當(dāng)深入探究四邊形時(shí),學(xué)生可以發(fā)現(xiàn)某些特殊的角關(guān)系,如對(duì)角互補(bǔ),能夠揭示出四邊形邊的一些隱含性質(zhì).這些隱含的性質(zhì),不僅僅豐富了學(xué)生對(duì)四邊形的認(rèn)識(shí),也為他們解決四邊形問題提供了新的視角和方法.因此,在教學(xué)中,教師應(yīng)該引導(dǎo)學(xué)生不僅僅看到表面的性質(zhì),更要去挖掘和探索那些隱含的性質(zhì),從而培養(yǎng)學(xué)生深入思考,善于發(fā)現(xiàn),創(chuàng)新的能力.
參考文獻(xiàn):
[1]張美旋.“設(shè)計(jì)教學(xué)法”在初中數(shù)學(xué)復(fù)習(xí)課中應(yīng)用的有效性探微——以幾何課《平行四邊形》的模塊復(fù)習(xí)為例[J].南昌教育學(xué)院學(xué)報(bào),2015,30(03):96-99.
[2]黃東秀.淺談初中數(shù)學(xué)四邊形性質(zhì)探索的教學(xué)[J].現(xiàn)代閱讀(教育版),2013(04):165.
[3]張振.抽象思維培養(yǎng)仍是初中數(shù)學(xué)教育的魂——對(duì)“平行四邊形的判定”一節(jié)課的聽后感想[J].科技信息,2011(14):667+669.

