巧用一元一次不等式解決實際問題



【摘要】一元一次不等式是解決實際問題最基本的手段之一.本文通過實例,闡述如何使用一元一次不等式解決實際問題.通過分析問題中的不等關系,建立不等式模型,并通過求解得到最優解.
【關鍵詞】初中數學;一元一次不等式;解題
不等式是數學中一種重要的工具,它不僅可以用于求解數學問題,也可以用于解決實際問題.一元一次不等式是數學中最基本的不等式類型,具有簡單、易懂的特點,在解決實際問題中具有廣泛的應用.
1 解決問卷調查問題
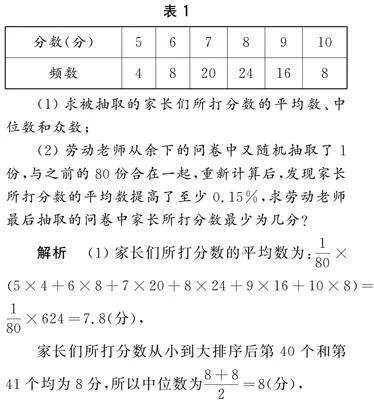
例1 某校為了解學生校外的勞動表現,對全校學生進行了問卷調查,讓每位學生的家長對自家孩子進行打分,滿分為10分(分數均為整數).勞動老師從全部的問卷中隨機抽取了80份,表1是家長所打分數的頻數統計表.
(1)求被抽取的家長們所打分數的平均數、中位數和眾數;
(2)勞動老師從余下的問卷中又隨機抽取了1份,與之前的80份合在一起,重新計算后,發現家長所打分數的平均數提高了至少0.15%,求勞動老師最后抽取的問卷中家長所打分數最少為幾分?
解析 (1)家長們所打分數的平均數為:180×5×4+6×8+7×20+8×24+9×16+10×8=180×624=7.8(分),
家長們所打分數從小到大排序后第40個和第41個均為8分,所以中位數為8+82=8(分),
有24位家長所打分數為8分,人數最多,所以眾數為8分.
(2)設勞動老師最后抽取的問卷中家長所打分數最少為x分,
依題意,得624+x80+1≥7.8×1+0.15%,
解得x≥8.7477,
因為x為整數,所以x的最小值為9,即勞動老師最后抽取的問卷中家長所打分數最少為9分.
點評 本題考查求平均數、中位數、眾數和一元一次不等式的應用.題設條件中明確了平均數至少提高了0.15%,暗示需要用平均數公式建立一元一次不等式關系.設勞動老師最后抽取的問卷中家長所打分數最少為x分,根據求平均數的公式可列出關于x的不等式,解之即可.
2 解決生活生產問題
例2 2022年3月25日,教育部印發《義務教育課程方案和課程標準(2022年版)》,優化了課程設置,將勞動從綜合實踐活動課程中獨立出來.為弘揚和傳承中華民族的傳統文化,強化勞動教育成果,錦江區某中學在端午節前夕,面向全體學生開展了包粽子比賽活動.已知A小組同學包的粽子個數y(個)與所用時間x(分)的關系如圖2所示.
(1)求y與x之間的函數關系式;
(2)若B小組同學每分鐘能包6個粽子,什么時候A小組同學包的粽子個數會超過B小組?
解析 (1)當0≤x≤10時,設y與x之間的函數關系式為y=kx,
把10,40代入解析式得40=10k,
解得k=4,
所以y=4x;
當x>10時,設y與x之間的函數關系式為y=mx+n,
把10,40,15,80代入解析式,
得10m+n=4015m+n=80,
解得m=8n=-40,
所以y=8x-40,
綜上所述,y與x之間的函數關系式為
y=4x0≤x≤108x-40x>10.
(2)根據題意B組同學包的粽子個數y(個)與所用時間x(分)的函數解析式為y=6x,
所以當A小組同學包的粽子個數超過B小組時,8x-40>6x,
解得x>20,
所以20分鐘后A小組同學包的粽子個數會超過B小組.
點評 本題考查了一次函數和一元一次不等式的應用,讀懂題意,正確求出函數解析式是解題的關鍵.先求出B組同學包的粽子個數y(個)與所用時間x(分)的函數解析式,再根據A小組同學包的粽子個數會超過B小組,列出一元一次不等式,解不等式即可解決問題.
3 解決商品購置問題
例3 在“垃圾分類,你我有責”活動中,某校準備購買A,B兩類垃圾桶共40個,其中A類垃圾桶的個數不多于B類垃圾桶的個數的2倍,設購入A類垃圾桶x個(x為整數).
(1)求最多能購買幾個A類垃圾桶;
(2)若A類垃圾桶單價為25元,B類垃圾桶單價為45元,則購買兩類垃圾桶最少需要多少元?
解析 (1)因為該校準備購買A,B兩類垃圾桶共40個,且購入A類垃圾桶x個(x為整數),
所以購入B類垃圾桶(40-x)個.
根據題意得x≤2(40-x),
解得x≤803,
又因為x為整數,
所以x的最大值為26,即最多能購買26個A類垃圾桶.
(2)設購買兩類垃圾桶共花費y元,
則y=25x+45(40-x),
即y=-20x+1800,
因為-20<0,
所以y隨x的增大而減小,
所以當x=26時,y取得最小值,最小值=-20×26+1800=1280,
所以購買兩類垃圾桶最少需要1280元.
點評 本題考查了一元一次不等式的應用以及一次函數的應用.根據購入A類垃圾桶的個數不多于B類垃圾桶的個數的2倍,可列出關于x的一元一次不等式,解之可得出x的取值范圍,再取其中的最大整數值,即可得出結論.設購買兩類垃圾桶共花費y元,利用總價=單價×數量,可得出y關于x的函數關系式,再利用一次函數的性質,即可解決最值問題.
4 結語
可見,在使用一元一次不等式解決實際問題時,需要仔細分析問題中的不等關系,建立適當的不等式模型,然后適當選擇不等式參數,以適應不同的問題需求,再運用適當的數學方法(如代入法、公式法等)求解不等式,得到最優解,最后根據實際情況,對求解結果進行解釋和討論.本文通過實例闡述了如何使用一元一次不等式解決實際問題.通過分析問題中的不等關系,建立不等式模型,并通過求解得到最優解.在實際應用中,需要根據不同的問題需求選擇適當的不等式類型和參數,并運用適當的數學方法求解最優解.一元一次不等式作為一種簡單、易懂的數學工具,在解決實際問題中具有廣泛的應用前景.
參考文獻:
[1]鞏虎琴.巧編題目解決問題——以“一元一次不等式解決實際問題”一課教學為例[J].甘肅教育,2016(18):124.
[2]陳東進.用一元一次不等式(組)解決實際問題[J].初中生世界,2016(21):69-70.
[3]王照堂.實際問題與一元一次不等式教學設計[J].數學學習與研究,2011(17):39.

