基于核心素養的小學數學“教—學—評”一體化研究

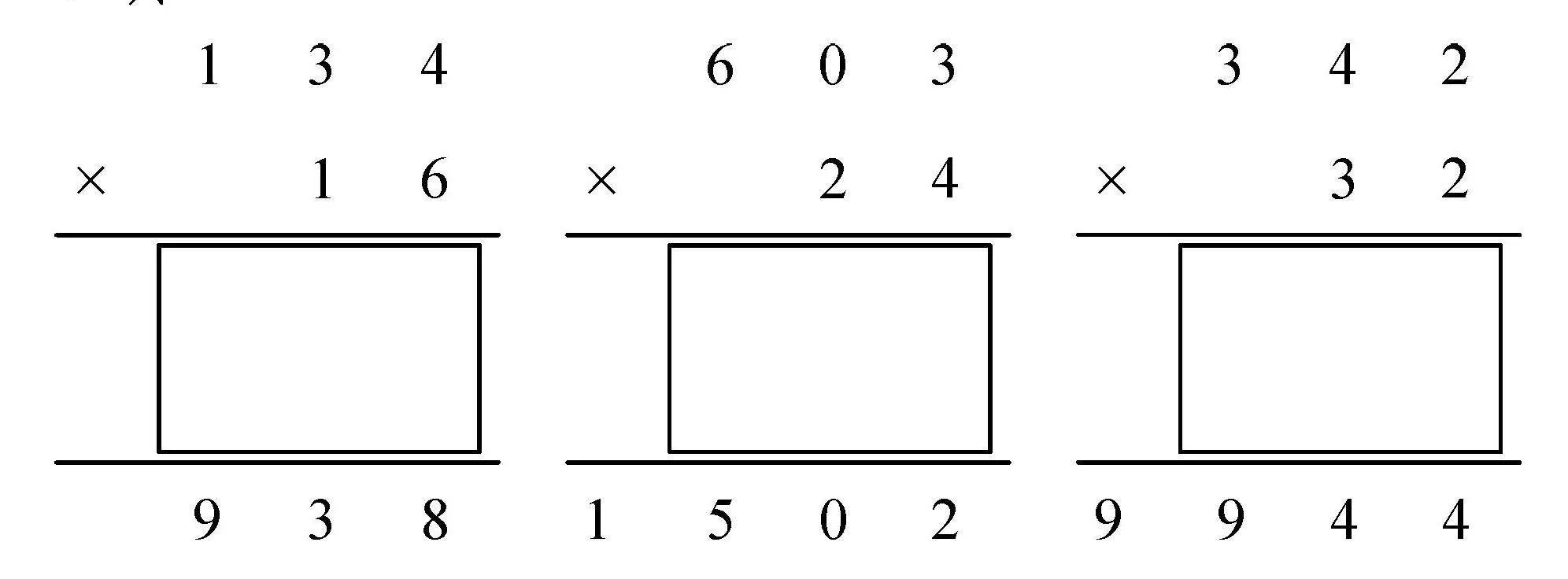
摘 要：

新課標明確提出了“教—學—評”一體化的要求，并予以細致指導.在此背景下，如何以數學核心素養為導向，基于學業質量標準，落實“教—學—評”一體化成為中小學教學改革的重點，也對一線教師提出了新的要求和挑戰.本文構建了核心素養導向的小學數學“教—學—評”一體化設計工具，旨在為教師落實“教—學—評”一體化理念提供工具幫助.

關鍵詞：核心素養；小學數學；“教—學—評”一體化；數與算數

《義務教育數學課程標準（2022年版）》

（以下簡稱“新課標”）

背景下，“教—學—評”一體化旨在以目標為導向確定評價標準，指導教師的教與學生的學.在此背景下，本文以小學數學“數與運算”知識點教學為例，開展核心素養導向的小學數學“教—學—評”一體化研究，助力以數學核心素養為依據的學習目標的確定、評價標準的制定以及教學活動的設計，將數學核心素養的形成和發展貫穿教學始終，將數學核心素養的培養落到實處.

1 創設情境，導入新課

問題1 今年暑假，老師去領略了一番青藏鐵路的壯觀.我從福州市出發，先自駕到青海省西寧市，汽車行駛速度為65千米每小時 ，一共行駛了43小時.我想知道從福州市到西寧市一共行駛了多少距離？

生：65×43.

師：為什么用乘法？

生1：因為汽車行駛的速度是每小時65千米，一共行駛了43小時，也就是求43個65是多少，所以用乘法.

生2：65是汽車行駛的速度，43小時是汽車行駛的時間，要求總路程就用速度乘時間.

學生獨立計算后，教師利用投影儀展示學生的答案.

問題2 到達西寧市后，老師再從西寧市出發，乘坐青藏鐵路線，一路向西，到達拉薩市.列車運行速度為145千米每小時、列車行駛時間為21小時.請大家列式求出總路程.

生：145×21.

【設計意圖】新課程改革倡導“真情境”“真問題”.教師在數學教學時應將問題置于真實情境中，以真實的生活情境喚起學生的生活經驗，以學科情境喚起學生的認知基礎，使學生在面對富有挑戰性的問題情境時，整體調用已有知識、經驗、思想與方法.學生經歷問題求解、探究發現的過程，建立對新知的理解.［1］因此，在本節課的教學設計中，筆者創設了從福州市到拉薩市旅游的問題情境，既幫助學生回憶了“兩位數乘兩位數”的計算方法，又引出了本節將要學習的“三位數乘兩位數”，為學生比較兩者的異同并實現知識遷移提供了支架.

教學評價：本環節的設計旨在幫助學生在復雜的問題情境中提取與問題相關的數學信息，培養學生的數學信息素養和“用數學的眼光觀察”的能力.相比于教材中的例題，該問題情境蘊含的數學信息較多，學生需要將汽車和列車的速度與時間區分開并進行對應.從教學效果來看，學生在本環節的目標達成度較高.

2 理法交融，培養運算能力

2.1 豎式計算

師：145×21如何計算？具體步驟是怎樣的？

生：第一步，用21的個位1乘145，等于145，求的是1個小時行駛了145千米；第二步，用21的十位2乘145，等于290，求的是20個小時行駛了2900千米；最后一步，把兩層積相加，得到3045，求的是21個小時一共行駛的距離.

師：這里的145和290分別表示什么？

生：145表示的是145個一，末位對齊個位，290表示的是290個十，末位對齊十位.

2.2 算法多樣

師：除了豎式計算，還有哪些計算方法？

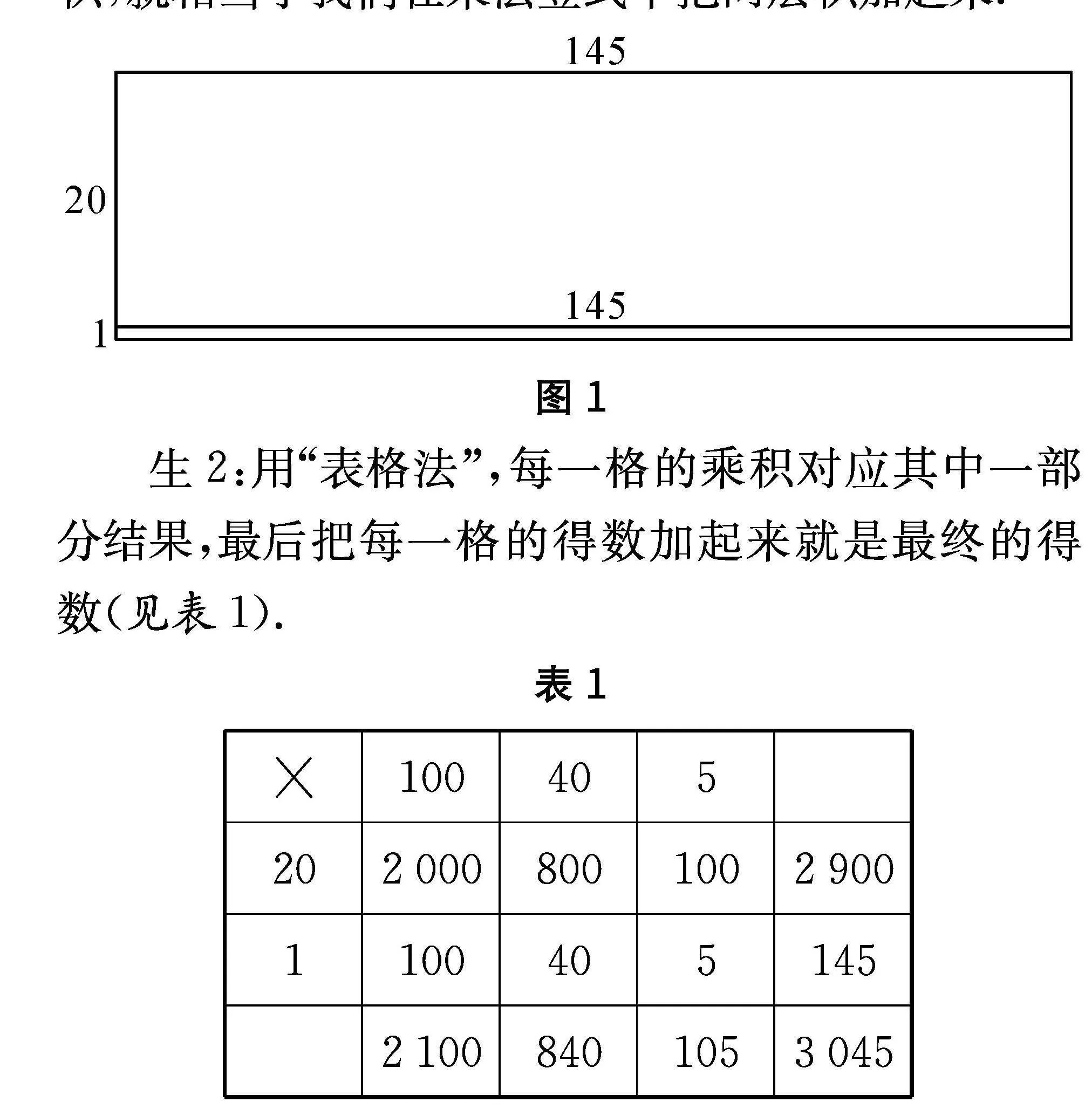
生1：將豎式計算轉化為求大長方形面積（如圖1）.上面大長方形的面積是145乘20，與豎式計算中第二層積計算的是一樣的，下面小長方形的面積是145乘1，與乘法豎式中第一層積表示的算式是一樣的.兩個長方形的面積之和等于整個大長方形的面積，就相當于我們在乘法豎式中把兩層積加起來.

圖1

生2：用“表格法”，每一格的乘積對應其中一部分結果，最后把每一格的得數加起來就是最終的得數（見表1）.

表1

100405

2020008001002900

1100405145

21008401053045

生3：第三種方法有點不一樣，把21變成3×7，將三位數乘兩位數轉化成三位數乘一位數.145×21=145×3×7=435×7=3045.

生4：第三種方法和第一種方法類似，都是把21進行拆分.第一種方法是將21拆成整十數和個位數，第三種方法是拆成兩個數相乘.

師：這兩種方法之間有怎樣的聯系？

生1：這些方法都是把乘數進行拆分，只不過拆分的方式不同，有的拆成兩個數相加，有的拆成兩個數相乘，但是最后都要把各部分加起來.

生2：我們剛才學的豎式計算也是這樣，列豎式計算是把第二個乘數拆成整十數和個位數，再分別去乘第一個乘數的每一個數，最后再把結果加起來.

生3：不管哪種方法，都是先拆分，再合起來.

2.3 對比類推，算法遷移

師：如果是三位數乘三位數，如“145×121”，算法有什么區別？

生：多一步用百位上的1去乘145，最后把三次的乘積加起來.

師：三位數乘兩位數是把兩次的乘積加起來，三位數乘三位數是把三次的乘積加起來.在計算時，用百位上的數去乘，得到的積就表示幾個什么？

生：表示幾個百.

師：以此類推，四位數乘四位數怎么計算？有什么變化？

生：四位數乘四位數要乘四次，第四次是用千位上的數字去乘，表示幾個千.

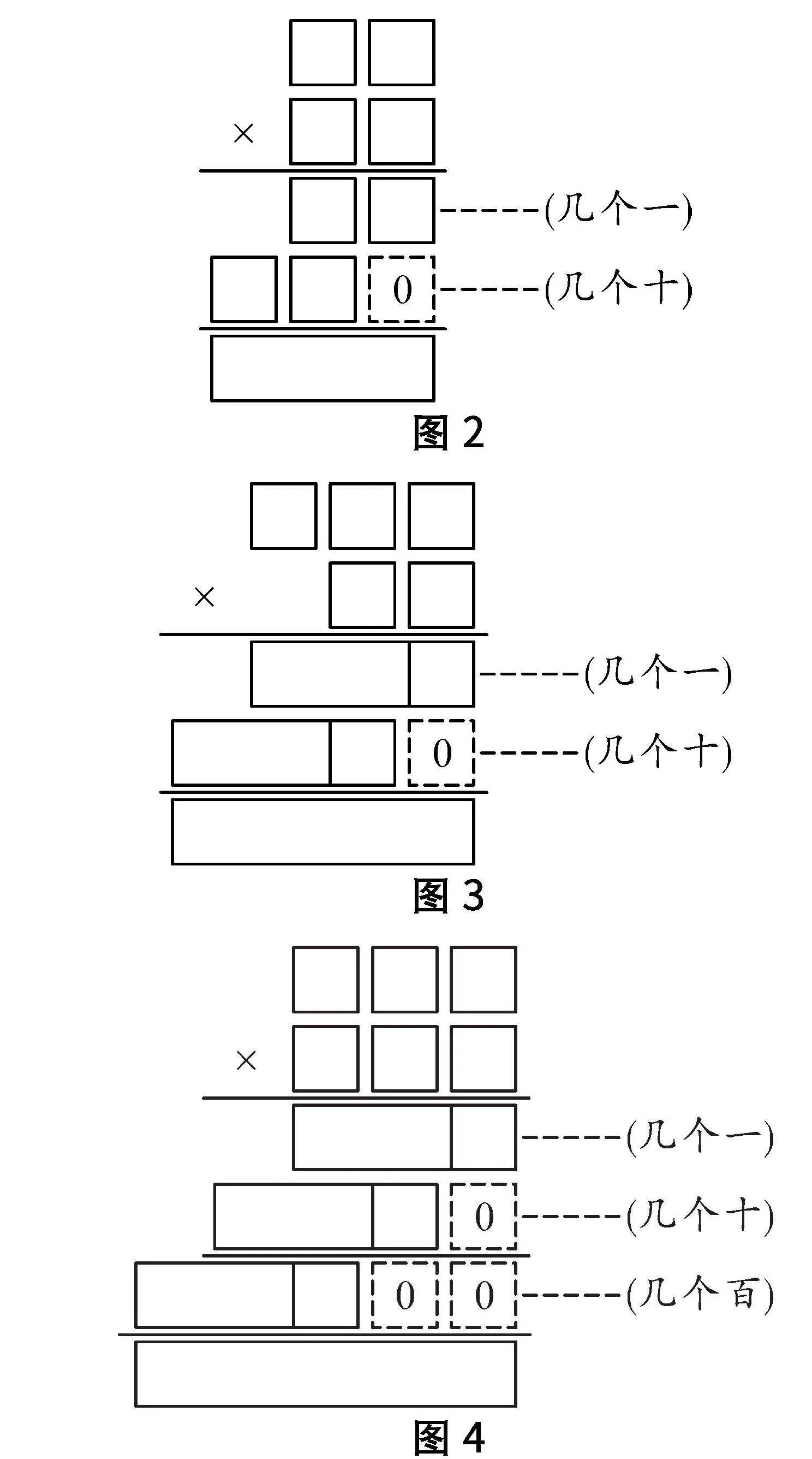
教師結合學生回答，在 PPT 上逐步出示如下乘法模型（如圖2、圖3、圖4）.

圖2

圖3

圖4

□□×□□

□□□

【設計意圖】學生對算理算法的理解程度對其運算能力的形成和發展具有重要作用.本環節的設計旨在通過多種算法引導學生發現算法和算理內在的“一致性”，深化其對算理算法的理解.［2］同時，教師在引導學生觀察對比的過程中，幫助學生逐步建立乘法模型.

教學評價：本環節的教學旨在幫助學生理解豎式中

每一步計算的是什么，表示什么含義.教學時，教師結合“面積圖法”與“表格法”幫助學生厘清算理并將“三位數乘兩位數”的算法擴展到“多位數乘多位數”，使學生建立乘法模型.在教學過程中，大部分學生雖然明白算理，但是無法用數學的語言邏輯清晰地表示出來.對此，教師在教學過程中應及時調整教學進度，通過不斷地追問、引導，帶領學生逐漸建立“乘法模型”.

3 鞏固練習，深化算理理解

（1）計算140×20.

生：這道題可以直接口算14×2或2×14，最后再把末尾的兩個“0”添上.

師：如果列成豎式，有什么辦法？具體計算過程是怎樣的？

生：列式時先不看末尾的兩個“0”，算出14×2=28，然后再添上末尾的兩個“0”，就等于2800.

師：列式計算時，為什么可以先不看末尾的兩個“0”？

生：因為“0”乘任何數都等于“0”.

（2）計算104×23.

師：如果把末尾的“0”放在乘數的中間，變成“104×23”，計算過程是怎樣的？

生：第一步先算“3×104”.

師：第二步用23十位上的2乘104，這個“2”代表的是什么？

生：兩個十.

師：算出來等于208，這里的208表示的是208個什么？

生：表示208個十，所以最后等于2392.

師：在計算時如果沒有進位的情況，要怎樣處理？

生：寫上“0”占位.

【設計意圖】乘數中間、末尾有“0”的兩類算式作為“三位數乘兩位數”教學中的兩類特殊計算，教學重點有所區別.對于乘數末尾有“0”的乘法，希望學生能在口算的基礎上探究豎式的簡便算法并理解末尾“0”不參與運算的原理；對于乘數中間有“0”的乘法，則重在對比有進位時和沒有進位時的情況.

教學評價：本環節的教學希望學生能根據“數的意義”解釋為什么在計算的過程中可以先不計算末尾的“0”，并借助乘數末尾有“0”的乘法豎式計算理解乘法運算的本質是“計數單位”個數的運算.在計算“末尾有‘0’”的乘法時，有三分之一的學生不知道在計算時可以先不將末尾的“0”參與運算，剩余的三分之二學生雖然知道簡便算法，但都認為是因為“0”乘任何數都得“0”，所以可以先不參與計算，未涉及算理層面.針對學生的表現，教師從“計數單位”的角度予以解釋.

4 辨析反思，培養估算能力

不計算，快速判斷這三道豎式計算題結果是否正確.

134×16

938

603×24

1502

342×32

9944

生：第一道題肯定錯，因為積不可能是三位數.

師：三位數乘兩位數的積不可能是三位數，那三位數乘兩位數的積可能是幾位數？

生：可能是四位數，也可能是五位數

師：有沒有可能是六位數？

生：沒可能.最大的三位數是999，最大的兩位數是99，即使都把它們往大估算，1000×100=100000，乘積是最小的六位數，所以三位數乘兩位數的積最大只可能是五位數.

師：那最小呢.

生：最小的三位數是100，最小的兩位數是10，100×10=1000，所以三位數乘兩位數的乘積最小是1000.

師：同學們說得都很清晰，借助計算器，我們知道剛才同學說的999×99=98901，所以我們可以確定三位數乘兩位數的乘積一定在什么之間？

生：1000～98901之間.

師：除了根據乘積的位數來判斷，我們還有什么方法可以直接判斷計算結果是否正確？

生1：可以用估算的方法.把603估成600，把24估成20，600×20=12000，因為兩個乘數都是往小估了的，所以結果一定比12000大，所以第二題肯定是錯的.

生2：也可以用看個位的方法.比如第一題，4×6=24，所以積的末尾一定是4.

【設計意圖】估算活動是促進學生數感發展的重要途徑，估算涉及對數字大小的理解能力以及修正調整數字的能力等.因此，在本課的教學過程中，教師設計“辨析反思”學習任務，引導學生在不計算的情況下，對“三位數乘兩位數”的積做出合理估算，旨在培養學生的估算能力，進而促進學生數感的發展.［3］

教學評價：在本環節的教學過程中，學生除了提出根據乘積的位數以及末位數字判斷計算結果是否正確外，還提出了利用“大、小估”的方式估計乘積的合理范圍，進而做出判斷，說明學生在本輪的學習中能夠有意識地進行估算且具備一定的估算能力.在介紹估算思路的過程中，學生能夠較為清晰地表達自己的思考過程，教學效果較好.

5 滲透文化，促進融會貫通

師：不同的國家在計算乘法算式時有不同的計算方法.讓我們通過一節數學微課，探究中國古代的“畫線法和算籌法”以及意大利的“格子算法”計算原理.

生1：這些方法只是寫法不一樣，形式不一樣，道理卻是一樣的.

和豎式一樣，都是用一個乘數的每一位去乘另一個乘數的每一位，都要“滿十進一”.

師：乘法計算的方法還有很多，除了我們今天學習的豎式計算，以及微課中介紹的格子算法、算籌法和畫線法之外，古埃及還有倍乘法，古印度、意大利還有豎式乘法.雖然方法不同，但是它們的道理都是一樣的，感興趣的同學課后可以用這些方法進行嘗試，并探索其他與眾不同的計算方法.

【設計意圖】本環節教師除了為學生提供教材中有關意大利“格子算法”的數學微課，還為學生提供了中國古代的“畫線法”與“算籌法”，通過多種方法的對比，幫助學生發現乘法計算本質上的共通之處，激發學生對數學文化的中國自信，鼓勵學生在前人的基礎上進行大膽創新.

教學評價：本環節設計希望學生通過數學文化的學習，建立起對數學文化的中國自信，激發對數學學習的興趣與熱愛.在教學過程中，“數學微課”的形式對四年級的學生有著較大的吸引作用，課堂上學生的注意力集中、興奮度高.

6 結語

核心素養導向的小學數學“教—學—評”一體化教學設計能夠促進學生數學核心素養形成與發展.在“教—學—評”一體化的設計中，學習目標始終發揮著“統領”作用，決定評價標準的制定以及教學活動的設計.以核心素養為導向的小學數學“教—學—評”一體化教學無論是在確定學習目標、制定評價指標還是設計教學活動中，都始終以核心素養為導向，將核心素養的培養貫穿始終.

參考文獻

［1］黃燕萍.基于核心素養的小學數學統計與概率“教—學—評”一體化研究［J］.教育界，2024（16）：53-55.

［2］李娟.探究“教—學—評”一體化課堂促進學生核心素養發展——以小學數學學科為例［J］.試題與研究，2024（3）：28-30.

［3］溫海澍.核心素養導向下小學數學“教—學—評”一體化教學評價探索——以人教版數學五年級下冊“長方體、正方體的認識”教學為例［J］.廣西教育，2023（22）：54-58.