基于機器學習算法的電機運行數據挖掘

摘要：文章以永磁電機的運行數據為研究對象，探討基于數據挖掘與機器學習算法的電機狀態分析與預測方法。首先，運用K均值聚類算法對采集的電機電壓、電流、扭矩、轉速等多種數據進行分類，揭示數據之間的潛在聯系。其次，采用K近鄰（KNN）算法對電機運行功率和繞組溫度進行回歸預測，結果表明該方法具有較高的預測精度。最后，通過構建和訓練神經網絡模型，對電機狀態進行更精確的預測，進一步驗證神經網絡在電機故障預警中的有效性。該研究為電機智能維護提供了技術支持，同時為工業領域的設備管理與優化奠定了基礎。

關鍵詞：電機；機器學習；數據挖掘；聚類；預測精度

中圖分類號：TP311；TM3" " " "文獻標識碼：A" " " 文章編號：1674-0688（2024）08-0066-04

0 引言

隨著永磁材料性能的持續改進及電力電子技術的飛速發展，永磁電機的應用范圍越來越廣，已滲透至軍工與民用領域，覆蓋從特殊到常規的各種應用場景，不僅在微特電機中占有優勢，還在電力推進系統中顯示出強大的生命力［1］。 鑒于工業生產環境中存在安全隱患，及時排查并消除機械設備中的潛在隱患和故障，確保工程運行的安全穩定與可靠，已成為一項至關重要的任務［2］。 電機作為工程機械的核心動力，其運行狀態直接影響整個系統的穩定性和生產效率，因此對其進行監測與分析顯得尤為重要。然而，傳統的電機狀態監測與故障診斷方法主要依賴于物理模型和經驗規則，解決思路是強化標準化安裝或是出了問題再維修，例如蘇紀陽［3］ 和郭海濤［4］針對水利泵站機電設備的不同部件進行了詳細分析，為水利泵站機電設備的安裝與故障檢修提供了全面的技術指導和參考；郭露丹［5］ 圍繞水利泵站設備的常見故障進行探討，根據故障類型與誘發原因，制定針對性的故障檢修措施。這些解決方案雖然在一定程度上取得了成效，但是在面對復雜多變的工業環境時，往往難以應對多維度、非線性的運行數據，從而影響診斷的準確性和實時性，并且可能延誤工期。近年來，隨著大數據技術和人工智能的發展，機器學習算法在數據挖掘與模式識別領域顯示出了強大的潛力。由于電機運行狀態數據稀缺且很少公開，因此國內針對工程設備電機數據挖掘的研究較少，主要停留在理論構想階段，如構建演示性數據挖掘信息平臺等［6］，鑒于此，本文基于實際工程電機數據的收集與分析，開展數據挖掘的初步研究。通過結合算法模型，對電機運行數據進行分析，提出一套有效的故障診斷和預測方法，為電機的智能化運行管理提供理論支持和實踐指導。

1 相關理論及算法

1.1 數據預處理

采用歸一化方法進行數據預處理，將每項分數除以總分，得到［0，1］區間內的小數值。歸一化常用于機器學習的預處理階段，當數據集的特征之間具有不同的取值范圍時，對數據進行歸一化是非常有必要的，其目的是統一各特征的度量尺度。歸一化公式如下。

[Xnorm=X?XminXmax?Xmin]，" " " " " " " " " " "（1）

其中：[Xnorm]是歸一化后的數據，X為原始數據，[Xmax]是最大數據，[Xmin]是最小數據。

1.2 K均值聚類算法

起初，K均值聚類算法在不同科學研究領域被獨立地提出，直到1967年，由James MacQueen教授提出“K-Means”這一術語，標志著該算法被廣泛認知、推廣和應用，并發展出眾多不同的改進算法。K均值算法流程如下。

（1）根據設定的聚類數，隨機選擇K個Cluster Centroid（聚類中心）。

（2）評估各個樣本到聚類中心的距離，如果樣本距離第K個聚類中心更近，則認為其屬于第K簇。

（3）計算每個簇中樣本的平均位置，將聚類中心移動至該位置。

（4）重復以上步驟直至各個聚類中心的位置不再發生改變。

1.3 K近鄰分類算法

K近鄰分類算法（K-Nearest Neighbor，KNN）是一種被廣泛使用的監督學習算法，其核心原理如下：對于任一給定的測試樣本，利用某種距離度量機制找到訓練集中最接近的K個樣本（即“鄰居”），隨后基于這些鄰居的信息進行預測。在分類任務中，通常采用“投票法”確定預測類別，即選取K個樣本中出現頻率最高的類別作為預測結果；而在回歸任務中，則采用“平均法”計算預測值，即取這些樣本的實際輸出值的平均值作為預測輸出。此外，還可根據樣本之間的距離進行加權平均或加權投票，其中距離較近的樣本會被賦予更高的權重。

對于給定的測試樣本[x]，如果其最近的鄰居樣本為[z]，那么最近鄰分類器的出錯概率表示為

[Perr=1?c∈yPc|xPc|z] ，" " " " " " "（2）

其中：P（err）代表出錯概率，P（c|x）、P（c|z）分別表示x和z同屬類c的概率，y表示所有類別。出錯概率等于1減去不出錯的概率。

假設樣本是獨立同分布的，并且對于任意x和任意小正數δ都能在δ的距離范圍內找到訓練樣本，即在每個測試樣本中總能在非常近的范圍內找到公式中的訓練樣本z。假設[c?=argmaxc∈yPc|x]表示貝葉斯最優分類器的結果，則有

[Perr=" 1?c∈yP（c|x）P（c|z）" " " " "?1?c∈yP2（c|x）" " " " "≤1?P2c?|x" " " " "=（1+P（c?|x））（1?（Pc?|x））" " " " "≤2（1?P（c?|x））。]" " " " " （3）

盡管最近鄰分類器的實現較為簡單，但其泛化誤差率不會超過貝葉斯最優分類器誤差率的兩倍，因此效果良好。

KNN能同時解決分類問題和回歸問題，本文采用分類的思路解決電機數據的回歸問題。KNN回歸問題的算法主要包括以下幾個步驟。

（1）準備數據集：將已知結果的樣本集合表示為向量形式，并且確定每個樣本的數值。

（2）選擇K值：確定用于劃分樣本空間的鄰居數量K，一般通過交叉驗證或經驗選擇一個合適的值。

（3）計算距離：對于待回歸樣本，計算其與所有已知樣本之間的距離。

（4）找到最近鄰：根據計算得到的距離，找到與待分類樣本距離最近的K個樣本。

（5）確定結果：根據最近鄰樣本的結果，通過求取K個近鄰樣本均值的方式確定待回歸樣本的數值。

（6）輸出結果：將計算的待回歸樣本的數值作為預測結果。

在K均值和K近鄰這兩種算法中，距離的度量都是核心要素，它直接決定了所選定的K個鄰近點，進而影響最終的預測結果。常用的距離度量方法有歐氏距離、曼哈頓距離等，本文主要采用歐式距離作為距離計算的依據，其公式如下：

[DX1， X2=x11?x212+x12?x222+···+x1n?x2n2]，" "（4）

其中：[DX1， X2]是距離，x是X中的每維數據。

1.4 神經網絡

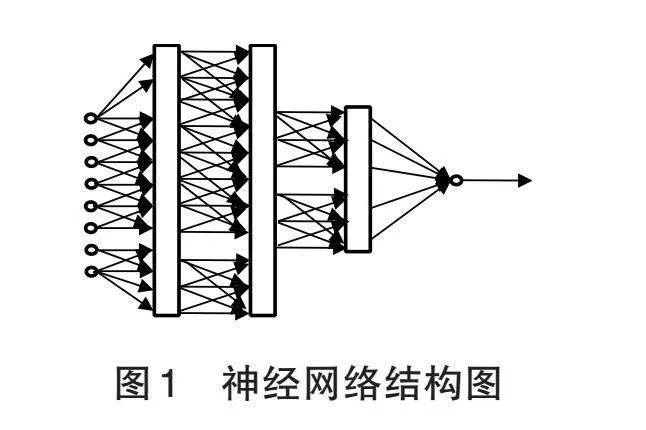
神經網絡由多個人工神經元組合而成，可以解決各種非線性問題，模型越復雜，解決非線性問題的能力越強。本文采用多層全連接神經網絡架構，該網絡包含3個隱含層（第一層神經元為256個，第二層為128個，第三層為128個），激活函數為ReLU；輸出層為單個神經元，激活函數為Sigmoid。神經網絡結構見圖1。

模型采用的損失函數為binary-crossentropy，損失函數公式如下：

[BCE（x）i=?[yilogfix+（1?yi）log （1?fix）]]， （5）

[BCE（x）final=i=1NBCE（x）iN]，" " " " " " " " （6）

其中：[BCE（x）i]為單個輸出單元的損失；[BCE（x）] final表示最終輸出損失；yi表示真實值，[fi（x）]表示實際輸出，N表示輸出的個數，本文中N=1。

2 電機數據挖掘

2.1 數據集

基于實際運行場景，采集永磁電機的運行數據，涵蓋電機的進線電壓、直流母線電壓、電機電壓、電機電流、電機扭矩、電機轉速、電機功率等參數，以及柜內濕度、柜內溫度、傳感張力、輸出張力、繞組溫度、前軸溫度、后軸溫度等環境與機械狀態信息，同時記錄運行狀態，共收集8 272條數據。

2.2 基于聚類算法的數據挖掘

科學建立于因果關系之上，在客觀事物產生的歷史數據中，各元素之間必然存在一定的聯系。隨著人工智能算法和大數據技術的出現，數據挖掘策略由傳統的明確路徑逐漸轉向融合機器學習等不明確的方法，從另一個角度發掘數據背后的聯系。通過解析數據之間的聯系，可透視現象背后的本質規律，并運用數據對系統運行進行可視化展示、實時監控和精準預測。本文采用K均值算法對既有數據進行聚類，從而挖掘數據之間的聯系。

2.3 基于KNN的數據預測

KNN作為一種簡單而有效的監督學習方法，已被廣泛應用于分類和回歸問題中。KNN通過基于距離的相似性進行預測，其直觀性和易于實現的特點使其在處理電機運行數據時具有顯著的優勢。通過詳盡分析電機運行數據，運用KNN對電機的未來狀態進行預測。研究將包括KNN的基本原理、參數選擇及其在電機數據中的應用實例。通過實驗驗證，可展示KNN在電機狀態預測中的有效性和優勢，并為電機的智能維護和故障預警提供有力的工具和方法。本文使用現有電機數據作為數據集進行KNN運算，并通過其他數據預測運行功率和運行溫度，從而實現對潛在電機故障的預警。

2.4 基于神經網絡的數據預測

神經網絡作為一種強大的機器學習技術，已經在許多領域展現出卓越的預測能力。特別是在處理非線性、高維數據方面，神經網絡能夠通過學習復雜的數據模式，提供更準確的預測結果。近年來，深度學習和神經網絡的快速發展為電機數據預測提供了新的視角和方法。通過構建和訓練神經網絡模型，可以有效地從電機運行數據中挖掘出潛在的規律，進而實現對電機未來狀態的準確預測。通過實驗驗證，神經網絡學習方法適用于電機狀態的預測，能幫助應用方解決電機智能維護和故障預警中存在的故障數據無法追溯、故障報警不及時等問題。與KNN相同，該部分的實驗也是選擇通過其他數據預測當前電機運行功率和運行溫度，利用數據集對神經網絡模型進行訓練，從而對電機故障進行預警。

3 實驗結果

3.1 實驗環境

編程使用Python3.9.13下的Anaconda解釋器并鏈接PyCharm IDE完成。使用的核心庫包括numpy 1.21.5，pandas 1.4.4，scikit-learn 1.0.2，TensorFlow 2.6.0，matplotlib 3.5.2，等等。電腦配置為CPU Intel（R） Core（TM） i7-10510U，RAM 16GB。

3.2 數據預處理

本實驗采集的數據種類較多且量綱各不相同。因此，為避免數據尺度影響算法，采用歸一化的方法對數據進行預處理，首先求得數據的最大值和最小值，通過歸一化映射公式將數據映射到0～1。

3.3 基于聚類算法的數據挖掘結果

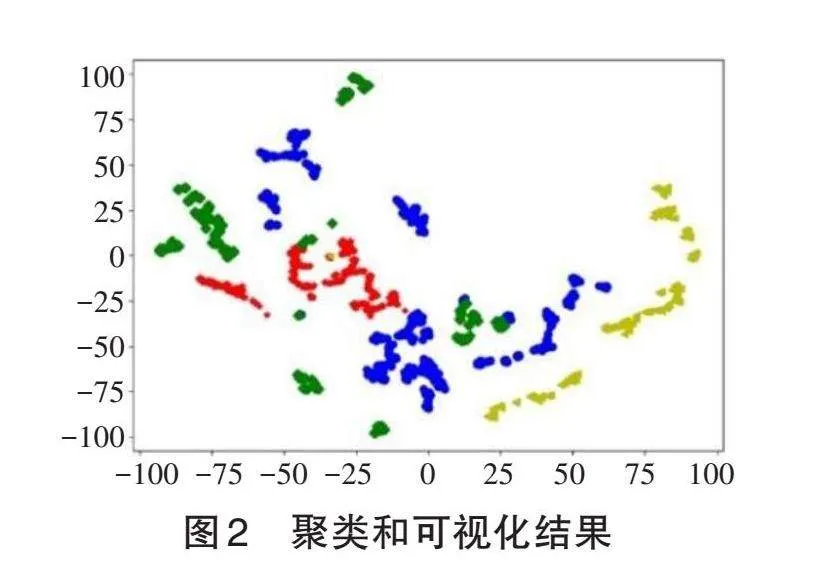
本實驗使用K均值算法對預處理后的歸一化數據進行聚類處理，具體設定聚類數目K為5，并使用t-SNE（t-distributed Stochastic Neighbor Embedding）降維方法進行降維，以便進行可視化處理。聚類和可視化的結果見圖2。

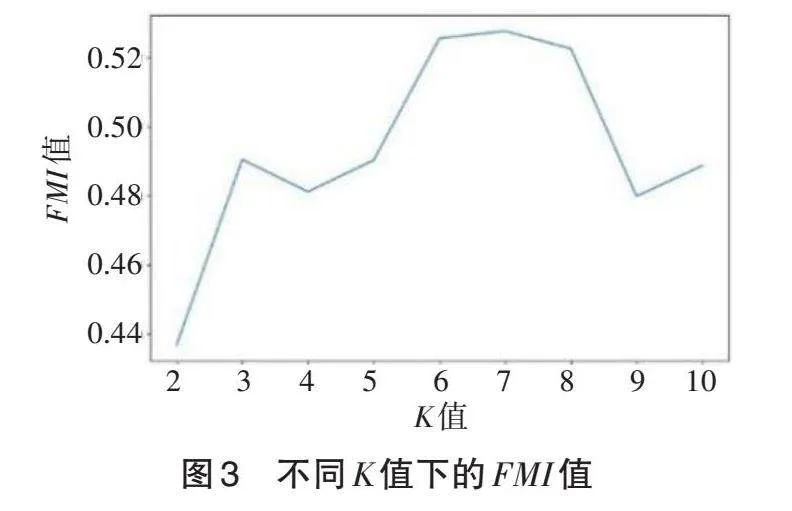
同時，為了更好地挖掘數據之間的關系，在實驗中對K值進行調整，并計算了不同K值下的FMI（Fowlkes-Mallows Index）值（見圖3）。

實驗結果表明，數據之間具有一定的關聯性，同類數據內部具有一定的共同性，而不同類數據之間呈現明顯的差異性。這說明數據存在一定的聯系，可以進行深度挖掘。

3.4 基于KNN的數據預測結果

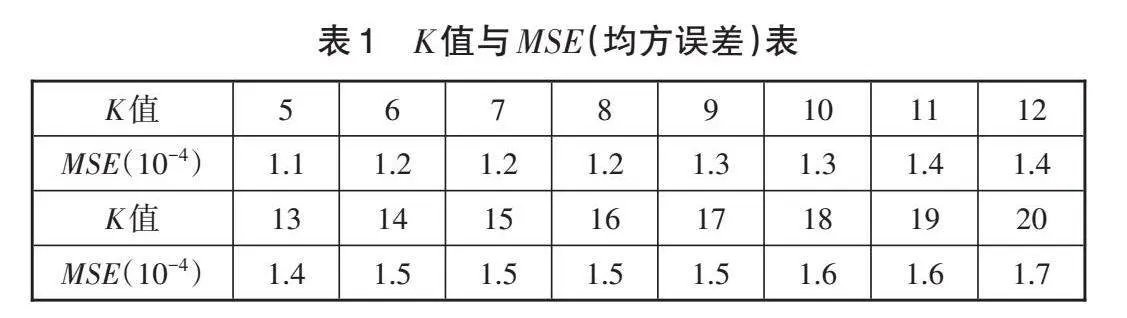
本文利用KNN解決了兩個回歸問題：一是基于進線電壓、直流母線電壓、電機電壓、電機電流、電機扭矩、電機轉速、柜內濕度、柜內溫度、傳感張力、輸出張力等特征數據，預測電機的功率；二是利用上述多維特征數據，預測電機的繞組溫度。首先將初始數據歸一化，然后將數據按照8∶2的比例劃分為訓練集和測試集，并且選擇K值完成數值的預測。實驗表明，采用KNN進行數據預測具有一定的準確性，整體均方誤差很小，并且K值越小，準確度越高。K值與MSE（均方誤差）表見表1。

3.5 基于神經網絡的數據預測結果

神經網絡作為一種多功能的機器學習模型，與KNN一樣，能夠解決分類、回歸問題乃至生成問題。本研究運用神經網絡解決回歸問題，用以預測電機的功率和繞組溫度。首先將初始數據進行歸一化處理，然后按照8∶2的比例將數據集劃分為訓練集和測試集，前者用于訓練，后者用于模型測試。網絡架構設計方面，采用了1個多層全連接神經網絡。訓練過程中，設定學習率為0.000 01，迭代次數為100次，每次迭代處理50個樣本。經過上述訓練，所構建的神經網絡模型在測試集上展現出了良好的預測性能，準確率可以達到90%以上。

4 結語

本文基于K均值聚類算法、KNN分類算法和神經網絡等多種方法對電機運行數據的挖掘與預測展開了深入研究。實驗結果顯示，K均值聚類算法有效地揭示了數據之間的潛在聯系，KNN分類算法和神經網絡則在電機運行功率和溫度的預測中展示了較高的準確性。實驗結果驗證了使用機器學習技術對電機數據進行分析和預測，不僅能提高電機的運行效率，還為智能維護和故障預警提供了可靠的技術支持。未來，隨著算法的進一步優化和數據量的持續增長，電機數據挖掘技術將在工業領域發揮更為重要的作用。本文雖然采用了神經網絡對電機運行數據進行挖掘與預測，但是模型結構相對簡單。下一步可以引入更復雜的深度學習架構，如卷積神經網絡、長短期記憶網絡等，進一步提升預測性能。同時，可以探索自適應學習率和自動超參數調整等優化方法，以提高模型的訓練效率。

5 參考文獻

［1］李玲玉.永磁電機在水利大型低揚程水泵上的適用性［J］.水利技術監督，2021（5）：149-152.

［2］賈豐收.水利工程機械安裝與維護策略分析［J］.地下水，2019，41（1）：226-228.

［3］蘇紀陽.水利泵站機電設備安裝及檢修技術分析［J］.現代制造技術與裝備，2023，59（12）：134-136.

［4］郭海濤.大型水利泵站機電設備安裝與檢修分析［J］.工程技術研究，2022，7（14）：111-113.

［5］郭露丹.水利泵站設備故障分析與管理維護措施探究［J］.中國設備工程，2023（17）：64-66.

［6］吳建蓉，楊濤.數據挖掘技術在水利水電工程中的應用［J］.水利水電科技進展，2022，42（5）：129.