ZL114A 鋁合金本構關系與失效準則參數的確定

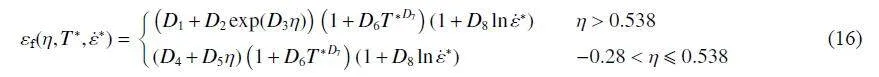
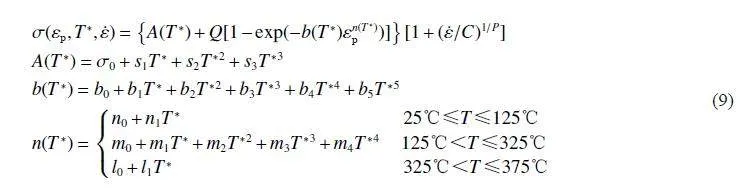
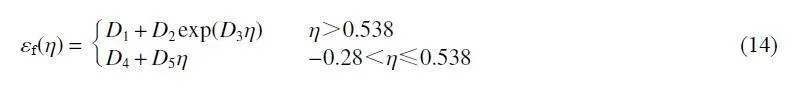
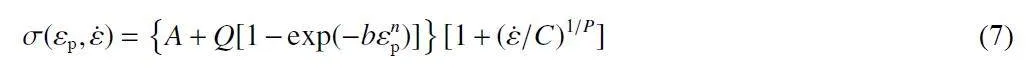
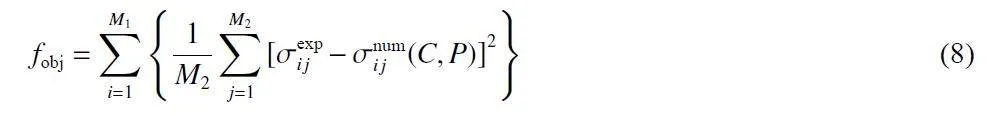
摘要： 針對航空發動機機匣材料ZL114A 鋁合金，構建描述該材料在較大溫度范圍下大變形及失效行為的材料模型。通過萬能試驗機及分離式霍普金森壓桿試驗裝置測試ZL114A 鋁合金在常溫準靜態、高溫和高應變率下的力學性能，分析溫度和應變率對材料流動應力的影響。采用有限元程序和優化算法反求25～375 ℃ 內材料的硬化參數，結合高應變率（1 310～5 964 s?1） 下材料的動態行為關系，構建包含塑性應變、溫度及應變率的經驗型本構模型。開展缺口拉伸、缺口壓縮等試驗并建立相對應的有限元模型，獲取材料在不同應力三軸度下的失效應變，標定分段形式的Johnson-Cook （J-C） 失效準則參數。通過不同溫度下的平板侵徹試驗和數值模擬驗證失效準則及其參數的有效性。結果表明，ZL114A 鋁合金具有明顯的應變硬化、溫度軟化及高應變率強化特性；具有應力飽和特征的Hockett-Sherby （HS）硬化模型較為準確地描述材料大變形下的力學行為；構建的材料本構關系可以描述ZL114A 鋁合金在大應變、寬溫度、高應變率下的力學行為；分段形式的失效準則具有預測不同溫度下材料失效行為的能力。

關鍵詞： ZL114A 鋁合金；本構關系；反求；失效準則；侵徹

中圖分類號： O344.3; TG146.2+1 國標學科代碼： 13015 文獻標志碼： A

航空發動機在工作過程中內部工況十分復雜，其葉片受疲勞損傷、外物打擊等因素影響極有可能發生斷裂故障。高速高能碎片穿透機匣易擊傷飛機關鍵部位（機艙、油箱、控制線路等），嚴重危及飛行安全[1]。為此，航空發動機適航規定[2] 中有專門條文提出發動機機匣應具備包容葉片損壞件的能力，通過整機包容測試是獲得適航許可的必要環節。由于真實發動機包容測試難度大、費用高，重復測試將極大增加研制成本，因此數值模擬成為研制前期機匣包容性評估及結構設計的重要手段。材料模型是采用數值模擬方法研究金屬結構動態力學行為的基本依據，其準確性很大程度上影響數值的模擬結果有效性[3]。

材料的塑性流動行為由本構關系描述，目前主要使用的本構關系可分為：基于材料微觀物理機制的物理型本構模型和基于實驗宏觀表現的經驗型本構模型。物理型本構模型基于由位錯動力學理論發展而來的熱激活理論，模型參數與材料微結構特征及其演化形式密切相關[4]，該類模型往往形式復雜，模型參數標定較為困難，具有代表性的模型為Zerilli-Armstrong （Z-A） 模型[5]。與物理型本構模型不同的是，經驗型本構模型具有形式簡潔、參數意義直觀等特點，如Johnson-Cook （J-C） 模型[6]、Fields-Backofen （F-B）模型[7] 和Khan-Huang （K-H） 模型[8] 等，其中J-C 本構模型[6] 考慮金屬材料應變硬化、應變率強化和溫度軟化等特性，廣泛應用于描述沖擊載荷下材料的力學行為。

基于J-C 本構模型的材料參數研究已取得一定的成果，相關研究表明J-C 本構模型能較好地預測金屬材料塑性行為[9-11]。標準形式的J-C 本構模型已內置于大型商用有限元軟件，如LS-DYNA、ABAQUS等，使其具有廣泛的應用性。辛春亮等[12] 歸納了常用材料的J-C 本構模型參數，為數值模擬提供了重要參考。近年來，數值模擬精度需求的提升對材料模型描述材料流動應力的能力提出更高的要求。學者們對J-C 本構模型形式進行了修正，使其更好地描述材料在不同溫度和應變率下的力學行為。由于材料種類和型號不同，修正形式各有差異，主要包括：（1） 引入混合硬化模型替換應變項[13-14]；（2） 應變項系數[15]、應變率項系數[16] 和溫度項指數[17] 等函數化；（3） 應變率項和溫度項整項替換[18]。

此外，J-C 模型參數標定方法主要為正向標定法。由于塑性材料拉伸過程中頸縮會導致試樣處于復雜的應力狀態，正向標定方法基于頸縮前試驗數據，標定后的模型預測材料大變形行為的適用性在部分研究中缺乏驗證。反求標定法以拉伸試驗的全過程數據為基礎，結合有限元技術和優化算法自動識別材料參數，在一定程度上彌補正向標定方法的不足。溫彤等[19] 通過有限元技術和優化算法識別22MnB5鋼的硬化參數，針對模型參數采用不同類型及工況下的拉伸試驗驗證，均得到良好的對標效果。茹一帆等[20]使用一種基于遺傳算法的反求標定方法獲得6005A-T6 鋁合金的硬化參數，得出描述不同應力狀態的材料行為時反求標定的參數更具適用性。

在強動載荷下，結構除了發生大的塑性變形以外往往伴隨失效斷裂。在描述韌性材料的失效行為方面，J-C 失效準則[21] 考慮應力三軸度、溫度和應變率對失效應變的影響，廣泛應用于沖擊、碰撞和侵徹等領域。高玉龍等[22]、馬銘輝等[23]、周倫等[16] 分別開展6008 鋁合金、675 裝甲鋼和6061-T6 鋁合金的試驗，進而標定J-C 失效準則參數，并通過試驗驗證材料模型的有效性。考慮到不同應力狀態下材料失效機制的不同，Bao 等[24] 針對2024-T351 鋁合金開展拉伸、壓縮、剪切等材料試驗，研究發現應力三軸度與失效應變的關系難以采用單一函數表達，提出分段形式的J-C 失效準則。Teng 等[25] 指出標準形式的JC失效準則過高預測低應力三軸度范圍的失效應變，易導致由剪切和壓縮主導的失效行為預測不準確，提出應開展相應的剪切和壓縮試驗以確定應力三軸度與失效應變的關系。

ZL114A 鋁合金因其優異的可鑄性、較高的比強度、良好的耐腐蝕性和抗熱裂性，常用于制造航空發動機機匣[26-28]。目前，關于ZL114A 鋁合金本構模型和失效準則的研究尚少， 康福偉等[29] 通過熱壓縮試驗得到ZL114A 鋁合金在中低應變率下的熱變形本構模型，旨在為熱加工工藝提供理論依據。王伏林等[30]標定ZL114A 鋁合金在常溫條件應變率影響下的J-C 本構模型和失效準則，但在較大溫度范圍下該模型適用性不理想。為研究ZL114A 鋁合金結構受溫度影響同時在強動載荷下的大變形及失效行為，需開展較為全面的材料性能測試并構建準確合理的材料模型。

本文針對不同溫度下ZL114A 鋁合金結構數值模擬的需求，開展不同溫度下拉伸試驗和高應變率下的分離式霍普金森壓桿（split Hopkinson pressure bar， SHPB）試驗，研究材料在不同溫度和應變率下的動態力學行為；分析傳統硬化模型參數標定方法的適用性，通過有限元技術及優化算法反求不同溫度下材料的硬化參數；采用多項式擬合不同溫度下的硬化參數，構建包含塑性應變、溫度及應變率的經驗型材料本構關系；開展缺口拉伸、缺口壓縮和剪切等試驗并建立相對應的有限元模型，獲取材料在不同應力三軸度下的失效應變，標定分段形式的J-C 失效準則參數；開展不同溫度下的平板侵徹試驗和數值模擬，通過對比試驗和模擬結果驗證材料模型的有效性。

1 ZL114A 材料力學性能試驗

1.1 試樣及試驗條件

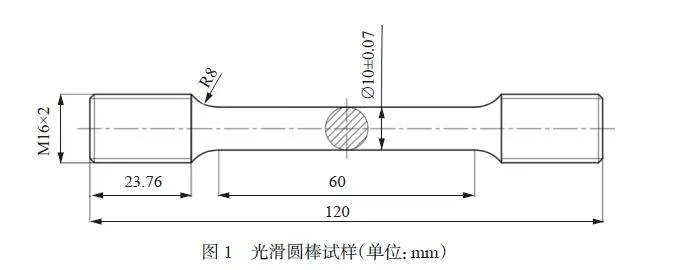
ZL114A 鋁合金化學成分[27] 如表1 所示，熱處理狀態為T6。單軸拉伸試樣依據GB/T 228.2—2015《金屬材料拉伸試驗方法》設計，標距段為60 mm，有效直徑為10 mm，詳細尺寸見圖1。常溫（25℃）試驗在萬能材料試驗機上進行，加載速率為3.6 mm/min，即名義應變率為1×10?3 s?1。通過安裝加熱保溫裝置完成多種溫度下的拉伸試驗，溫度范圍為125～375 ℃，溫度增量為50℃。

根據GB/T 34108-2017《金屬材料高應變速率室溫壓縮試驗方法》，采用SHPB 裝置完成高應變率下材料的動態力學試驗。參考文獻[31]設計2 種壓縮試樣，尺寸分別為 10 mm×5 mm和 6 mm×3 mm，以研究材料在較大應變率范圍下的動態力學性能。

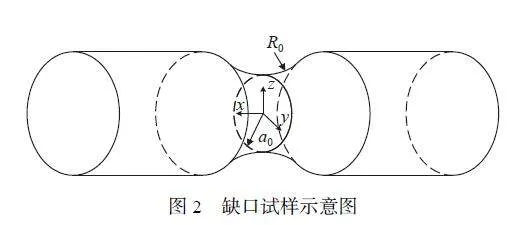
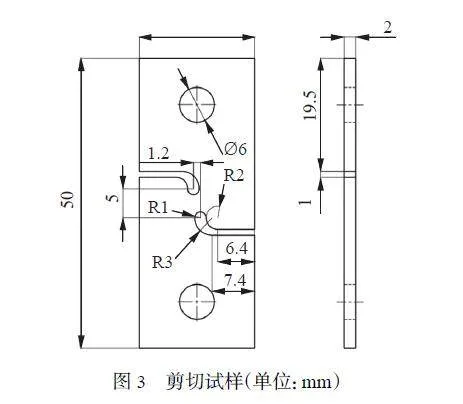
根據Bridgman 理論公式[32] 設計具有不同初始應力三軸度的缺口拉伸/壓縮試樣，確定拉伸/壓縮條件下應力三軸度與材料失效應變的關系。圖2 為缺口試樣示意圖，缺口拉伸試樣最小截面半徑a0 為5 mm，缺口半徑R0 分別為20、10和5 mm，分別記為R20 拉伸、R10 拉伸和R5 拉伸試樣。此外，光滑圓棒試樣可視為缺口半徑為無窮大的缺口試樣。3 種壓縮試樣高度為25 mm，有效直徑為10 mm，試樣的缺口半徑分別為無窮大、10 和5 mm，分別記為單軸壓縮、R10 壓縮和R5 壓縮試樣。參考文獻[33] 設計的剪切試樣，試樣厚度為2 mm，長度和寬度分別為50 和20 mm，如圖3 所示。

1.2 單軸拉伸與SHPB 試驗結果

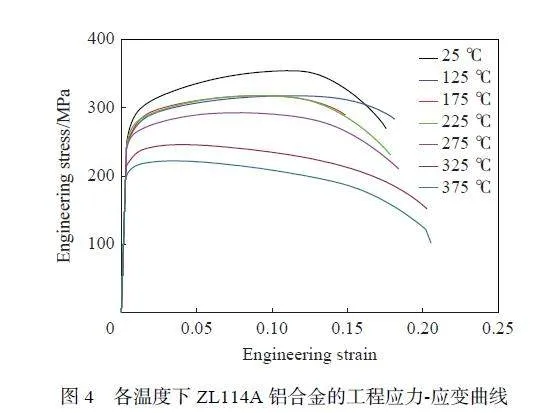
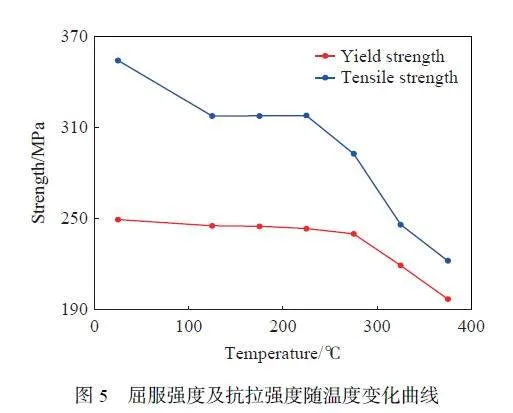
常溫和加熱條件下拉伸試樣位移數據分別由接觸式引伸計和萬能試驗機內置的位移傳感器獲得，由于加熱拉伸過程中位移傳感器引入設備彈性變形的誤差，因此加熱條件下工程應力應變曲線的彈性段部分以常溫拉伸彈性段進行替換。圖4 為各溫度下ZL114A 鋁合金的工程應力-應變曲線，隨著溫度升高，材料強度降低，工程斷裂應變整體上稍有提高。圖5 為ZL114A 鋁合金屈服強度及抗拉強度隨溫度變化曲線，在25～275℃ 范圍內，材料抗拉強度隨溫度的升高而減小，而屈服強度基本保持不變；溫度達275℃ 后，材料屈服強度開始降低，材料抗拉強度降低幅度增大。從圖4 可知，在125～225℃ 內，材料性能較為穩定，部分塑性流動曲線表現出較好的一致性。特別地，當溫度升到325℃ 后，材料工程應力經較小增幅后達到應力峰值，隨后應力緩慢減小。原因在于，鋁合金作為層錯能高的金屬，在溫度較高條件下發生塑性變形，位錯易發生交滑移和攀移，通常出現動態回復[34]。由于加工硬化與動態回復引起的軟化效應同時存在，兩種機制相互競爭下，材料硬化程度削減。隨著溫度的增加，材料動態回復效應加劇，當動態回復軟化速度超過硬化速度時，軟化效應占主導作用，材料硬化被動態回復所消除[3，35]。

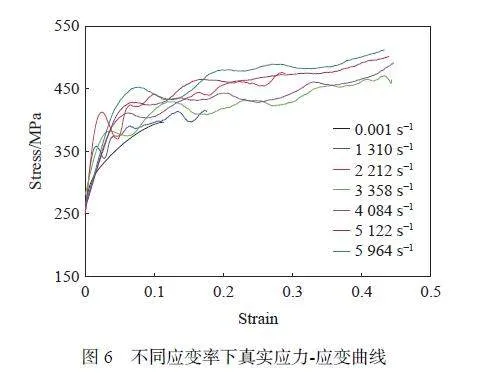
高應變率下材料的動態力學試驗中，通過SHPB 數據采集系統獲得入射桿和透射桿應變信號，基于一維彈性應力波及試樣應力、應變均勻性假定，采用二波法[36] 得到材料真實應力-應變曲線及對應的應變率。圖6 為多種高應變率和準靜態下材料真實應力應變曲線。從圖6 可知，ZL114A 鋁合金具有一定的應變率敏感性。應變率為1 310 s?1 時，材料流動應力與準靜態下差異較小，材料具有輕微的應變率強化作用；應變率在2 212 s?1 以上時，流動應力相比準靜態流動應力有較大增長，應變率強化效應較為顯著。在高應變率下，流動應力并不隨應變率增大而單調增加，應變率在2 212～3 558 s?1 范圍內時，材料流動應力呈下降趨勢。隨著應變率的提高，流動應力繼續增大，整體上表現出高應變率強化效應。材料應變率強化效應可解釋為，由于金屬材料塑性變形的機理主要是位錯運動，當變形速率達到一定值時，位錯滑移與強化相粒子發生強烈的交互作用，在晶格中遇到的阻力增大，因而呈現出較高的流動應力[37-38]。

2 不同溫度下材料硬化參數標定

2.1 材料硬化模型

材料硬化模型用于描述應變硬化行為對材料流動應力的影響，按應力增長有無上限，可分為飽和模型和非飽和模型[39]。

J-C 本構模型在只考慮應變強化效應的條件下可簡化為非飽和的Ludwik 硬化模型[40]：

σ = A+ Bεnp （1）

式中：σ 為流動應力， εp 為等效塑性應變，A 為屈服強度，B 為硬化系數，n 為硬化指數。

飽和硬化模型中具有代表性的模型為Hockett-Sherby （H-S） 硬化模型[41]：

σ= A+Q[1-exp（-bεnp）] （2）

式中：Q 為材料飽和系數，b 為硬化系數。

2.2 正向標定方法適用性分析

首先采用傳統正向標定方法標定上述硬化模型參數。在拉伸試驗中，材料在頸縮前后經歷均勻變形和局部集中變形兩個階段，材料處于非單軸拉伸的復雜應力狀態。因此，取頸縮前數據轉換為真實應力應變進行曲線擬合：

σt = σe（1+εe） （3）

εt = ln（1+εe） （4）

式中：σt、εt分別為真實應力和真實應變，σe、εe分別為工程應力和工程應變。

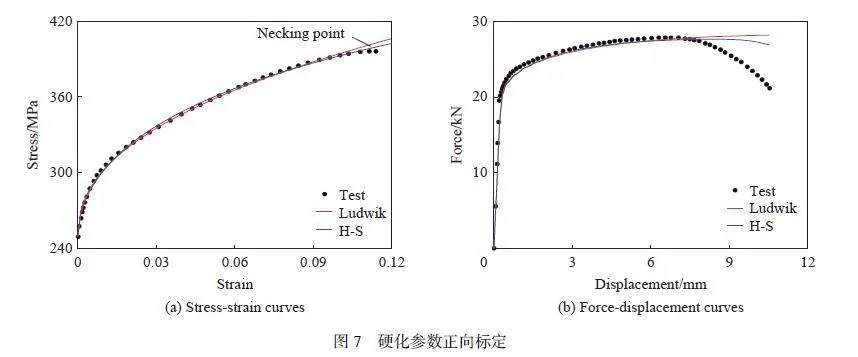
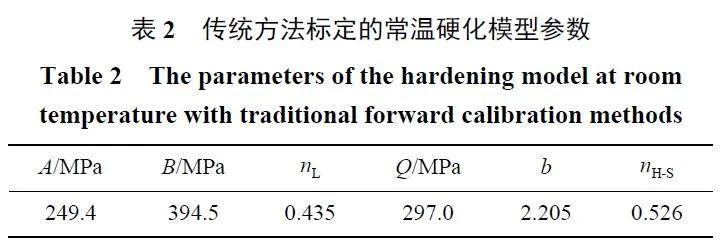
圖7（a） 為采用正向標定方法得到的常溫Ludwik 硬化模型和H-S 硬化模型擬合曲線，兩種硬化模型與試驗數據擬合度較高，均能較好反映材料在頸縮前的應力-應變關系，硬化參數見表2。基于LS-DYNA程序建立光滑圓棒試樣有限元模型，檢驗由正向標定方法獲取的模型參數在數值模擬中的預測能力。圖7（b） 為常溫拉伸試驗與數值模擬的載荷-位移曲線，兩種硬化模型均能很好地描述材料頸縮前的力學行為，而高估材料頸縮后的承載能力。這是因為材料頸縮后的應力-應變關系根據硬化模型外推得到，并未使用真實試驗中材料頸縮后數據，外推的應力-應變關系對材料頸縮后的力學行為缺乏預測精度。因此，傳統正向標定方法標定的硬化模型描述材料在大變形下的力學行為具有一定的局限性。

2.3 材料參數反求標定

針對采用傳統標定方法獲得的參數難以準確描述材料在大應變下力學行為的問題，因此基于拉伸試樣全過程載荷-位移數據，通過有限元技術以及優化算法獲取材料參數。通過優化算法調整有限元模型材料參數，以數值計算結果與試驗結果誤差最小為目標，反求得到最優材料參數。

2.3.1 參數反求實現

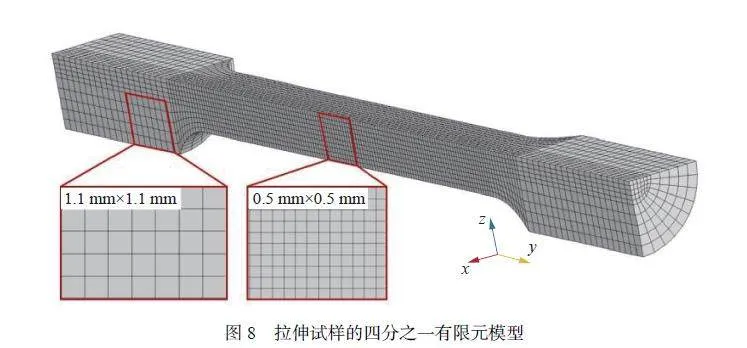
圖8 為拉伸試樣四分之一有限元模型，通過網格收斂性驗證，最終確定標距段截面網格尺寸為0.5 mm×0.5 mm，夾持段截面網格尺寸為1.1 mm×1.1 mm，整個模型單元數量為53 872。試驗中拉伸試樣螺紋段未發生明顯變形，有限元模型中簡化成光滑面，模型一端施加固定約束，另一端施加位移邊界條件。

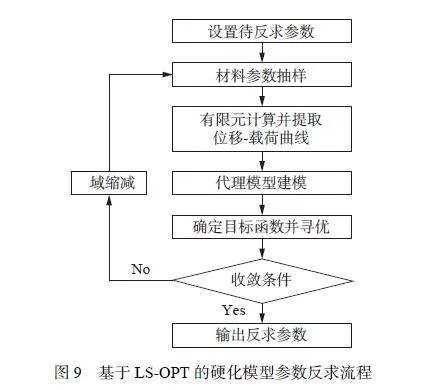
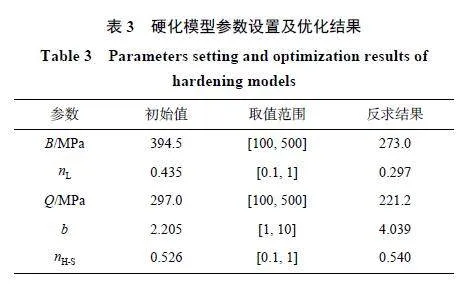
在材料參數反求中，由于反復調用有限元程序，為便于實現與優化程序LS-OPT 的數據交互，采用LS-DYNA 程序求解準靜態問題，通過控制加載時間和選擇合適的加載函數保證求解精度[42-43]。基于LS-OPT 的硬化模型參數反求流程如圖9 所示。Ludwik 硬化模型通過LS-DYNA程序中98 號材料進行設置，彈性模量為71 GPa，泊松比為0.33，屈服強度A 為249.4 MPa，硬化系數B 和硬化指數n 為待優化參數。由于LS-DYNA中缺少適用于體單元的H-S 硬化模型，基于徑向回歸法[44]，通過Fortran 語言編寫H-S 模型子程序嵌入至LS-DYNA 實現模型計算。H-S 模型中待反求的參數分別為飽和系數Q，硬化系數b 和硬化指數n。待反求參數的初始值根據正向標定的結果確定，參數的取值范圍如表3 所示。通過D-Optimal 取樣方法抽取參數樣本代入有限元模型計算，從計算結果中提取數值計算的位移-載荷曲線。代理模型的響應值為數值模擬與試驗位移-載荷數據點的均方誤差。參數反求目標函數的最優值應使得響應值最小，采用自適應模擬退火算法實現參數尋優。對優化值進行收斂性判斷，未滿足收斂條件則通過序貫響應面縮小代理模型的參數范圍，再次抽樣計算并構建新的代理模型；滿足收斂條件則輸出材料參數的優化值，即為反求參數。

2.3.2 參數反求結果

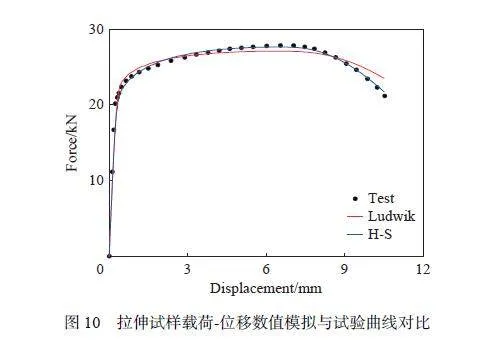
圖10 為優化后的數值模擬載荷-位移曲線與試驗曲線，硬化參數反求結果見表3。相比于傳統標定方法，反求標定的兩種硬化模型均能較好地描述材料頸縮后力學行為。其中，H-S 模型表現更優，較為準確地描述了ZL114A 鋁合金在室溫下拉伸全過程的力學行為。因此，采用H-S 硬化模型描述ZL114A 鋁合金在各溫度下的硬化行為。

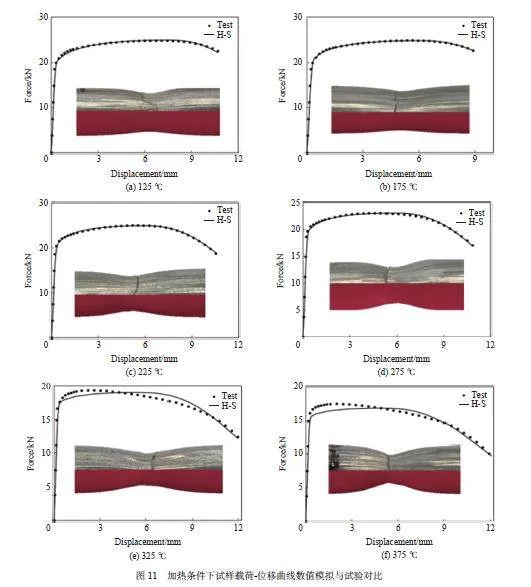
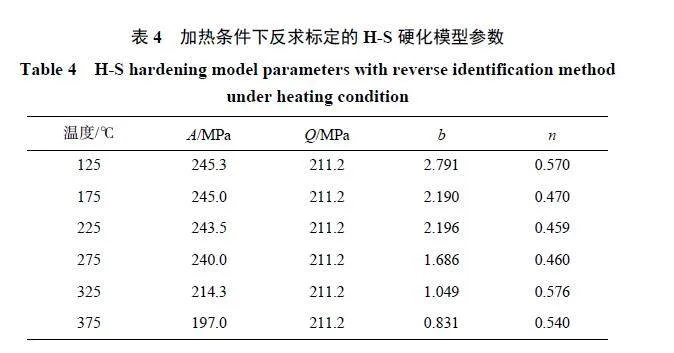
為構建ZL114A 鋁合金在較大溫度和應變率范圍內統一的的經驗型本構模型，需要減少隨溫度變化變量的數量，因此在材料硬化參數尋優時將加熱條件下硬化參數Q 同常溫拉伸一致，屈服強度A 由材料初始狀態直接確定，則待反求的參數為硬化系數b 和硬化指數n。采用上述方法對不同溫度下ZL114A鋁合金的H-S 硬化模型參數進行識別，圖11 為加熱條件下拉伸試樣的數值模擬和試驗載荷-位移曲線。在125～275 ℃ 內，試驗曲線變化趨勢與常溫時相似，彈性段后拉伸載荷經過較長的緩慢上升期，數值模擬與試驗位移-載荷曲線具有很好的一致性；在325～375 ℃ 內，ZL114A 鋁合金受溫度影響顯著提升，彈性段后拉伸載荷經較小增幅后開始下降。受溫度影響下材料微觀機制發生改變，宏觀上載荷曲線下降過程分為兩段，H-S 硬化模型無法描述這一行為，因此數值模擬曲線與試驗存在較小偏差。本文旨在構建經驗型本構模型并其應用于數值模擬，對涉及微觀物理機制的本構模型不作討論。從圖11 可知，H-S硬化模型整體上較好地描述材料在不同溫度下力學行為，且拉伸試樣最終頸縮形貌的數值模擬與試驗相似度較高，適用于描述ZL114A 鋁合金在大溫度范圍內及大變形下的力學行為。ZL114A 鋁合金的H-S硬化模型參數見表4。

3 J-C 本構模型修正與參數標定

3.1 J-C 本構模型修正

標準形式的J-C 本構模型為應變項、應變率項和溫度項三項乘積，表達式為：

σ（εp，T*，"˙ε） = （A+ Bεnp ） （1+Cln ˙ε*） （1-T*m） （5）

式中：σ為流動應力；εp為等效塑性應變；˙ε*為無量綱應變率，˙ε*=˙ε/˙ε0，˙ε為應變率，˙ε0為參考應變率；T*為歸一化溫度，T* = （T -Tr）/（Tm -Tr），T 為材料溫度，Tr、Tm分別為參考溫度（25 ℃）和材料熔化溫度（600 ℃）；A 為屈服強度；B 為硬化系數；n 為硬化指數；C 為應變率系數；m 為溫度軟化指數。

由J-C 本構模型乘積形式可知，無量綱的應變率項和溫度項作為縮放系數影響J-C 本構模型流動應力，而實質上材料在塑性變形階段的應力-應變關系主要由應變項—即硬化模型描述。由前述分析可知，H-S 硬化模型描述ZL114A 鋁合金在大變形下的力學行為優于Ludwik 硬化模型。因此，為準確描述ZL114A 鋁合金在較大范圍溫度和高應變率下的力學特性，對標準J-C 本構模型進行修正。以H-S 模型代替傳統J-C 模型中Ludwik 應變強化項，并將H-S 模型中部分參數視為溫度的函數。為體現材料對高應變率下流動應力的敏感性，將對數形式的應變率強化項替換為Cowper-Symonds 模型[45]，修正的J-C 本構模型（MJC）為：

σ（εp;T*; ˙ε） ={A（T*）+Q（1-exp[-b（T*）εn（T* ）p ）]}[1+（ ˙ε/C）1=P] （6）

式中：P 為應變率指數。

3.2 MJC 本構模型參數標定

3.2.1 應變項參數標定

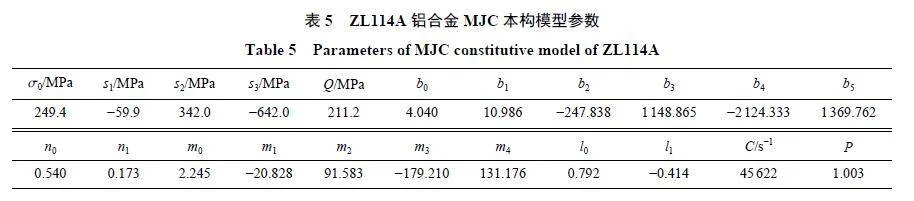
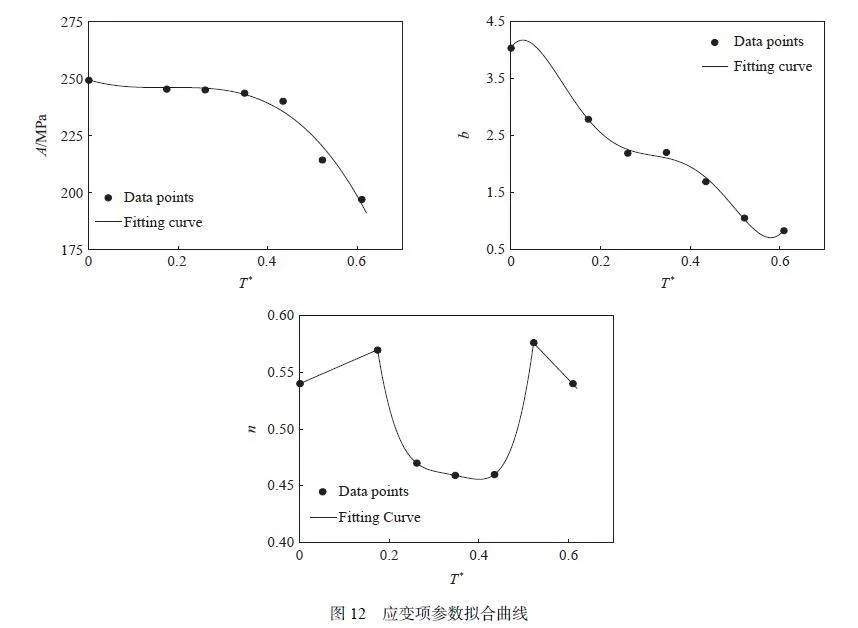
基于表3 和表4 數據擬合歸一化溫度T*與ZL114A 鋁合金初始屈服強度A、硬化系數b 和硬化指數n 的關系，結果如圖12 所示。從數據點可知，隨著溫度增加，初始屈服強度A 和硬化系數b 整體上減小，而硬化指數n 在0.45～0.60 內波動。為較好地在模型中反映已測數據，同時在一定程度上發揮模型對其他未測數據的預測作用，采用多項式進行數據擬合。其中，屈服強度A 和硬化系數b 分別用三次及五次多項式擬合，決定系數R2 的值分別為0.974 和0.997，相關性均良好；對于硬化指數n 則采用分段函數進行擬合，決定系數R2 的值為1。應變項各參數見表5。

3.2.2 應變率項參數標定

在應變率項參數標定中，MJC 本構模型溫度參數設為常溫，模型可簡化為：

由于應變項參數已標定，模型中待標定參數為應變率強化項的應變率系數C 和應變率指數P。為使本構模型較好地描述不同應變率下的應力流動行為，基于不同應變率下ZL114A 鋁合金真實應力應變數據（圖6），采用遺傳算法實現應變率項參數標定。以不同應變率下流動應力數據點對應的應力計算值與試驗值的均方誤差最小為優化目標，該尋優問題的目標函數為：

式中：M1 為各應變率下的試驗曲線數目，M2 為每條曲線上的數據點數目，σexpi j、σnumi j分別為第i 條曲線上第j 個數據點的試驗應力值和計算應力值。通過遺傳算法迭代尋優，進化次數為1 000 次，參數C 和P 的約束條件分別為1 000≤C≤100 000、0：5≤P≤5，參數C 和P 的最終優化結果見表5。ZL114A 鋁合金MJC 本構模型具體表達式為：

式中：σ0、s1、s2、s3、b0、b1、b2、b3、b4、b5、n0、n1、m0、m1、m2、m3、m4、l0、l1 為常數。

3.3 MJC 本構模型準確性評估

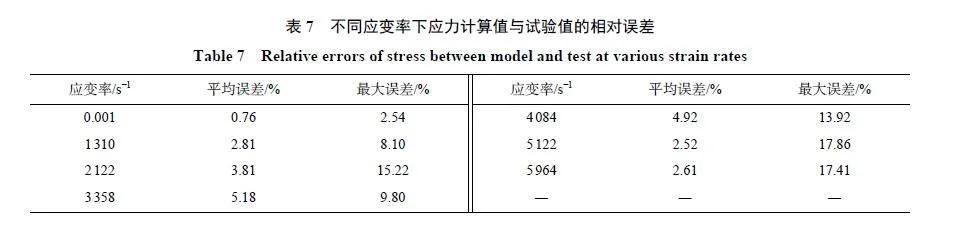
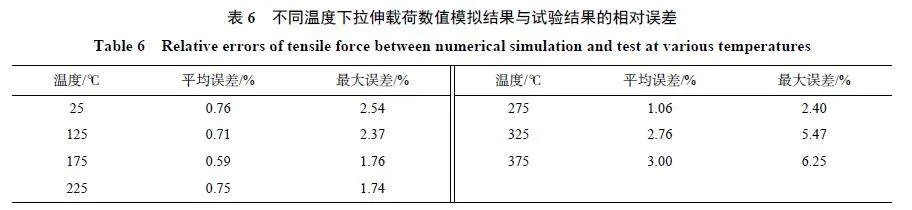
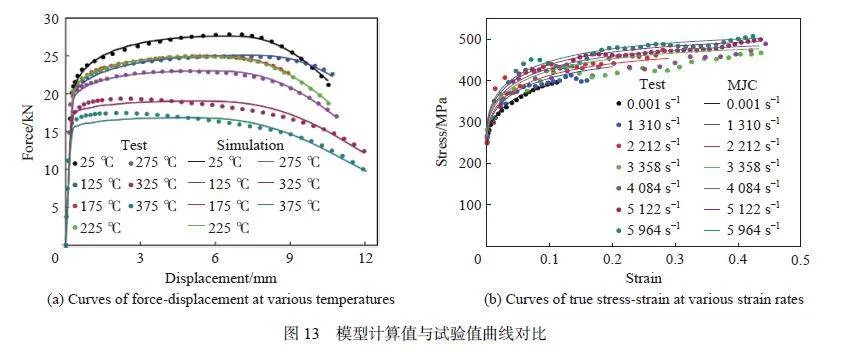
將考慮溫度影響的MJC 本構模型嵌入至LS-DYNA 有限元程序中，得到不同溫度下試樣的數值模擬載荷-位移曲線，如圖13（a） 所示。以拉伸載荷數值模擬結果和試驗結果的相對誤差為指標，評估不同溫度下本構模型的準確性，如表6 所示，各溫度下的平均誤差均低于3%，最大誤差低于7%，說明該本構模型能較好地描述不同溫度下ZL114A 鋁合金的力學行為。圖13（b） 為本構模型模擬和試驗結果的對比，為了評估本構模型描述不同應變率下的流動應力的準確性，以各應變率下應力的模擬與試驗結果的相對誤差為作為模型精確度評價指標，如表7 所示，平均誤差均低于6%，最大誤差低于18%。由于高應變率下試驗的應力-應變曲線呈不穩定的波浪形，因此最大誤差較大，但平均誤差保持在較低水平。整體而言MJC 本構模型在一定程度上能描述不同應變率下的流動應力。

4 J-C 失效準則參數標定

4.1 J-C 失效準則

J-C 失效準則以塑性應變累積為基礎，以損傷參數D 判斷材料失效，損傷參數D 定義為：

式中：Δεp 為等效塑性應變增量，εf 為失效應變。當D=1 時材料失效，在數值模擬中表現為單元刪除。J-C失效準則與材料本構關系為非耦合關系，累積損傷不影響材料流動行為。在J-C 失效準則中，失效應變εf 考慮應力三軸度、應變率及溫度對材料失效應變的影響，表達式為：

εf （η，"˙ε*，T*） = [D1 +D2exp（D3η）] （1+D4ln ˙ε*） （1+D5T*） （11）

式中：η 為應力三軸度，η=?p/σeff，p 為靜水應力，σeff 為von Mises 等效應力；D1～D5 為待標定參數。

4.2 失效準則參數標定

4.2.1 應力三軸度對失效應變的影響

Bridgman[32] 提出缺口拉伸試樣最小截面中心的應力三軸度計算公式：

式中：a0 為最小截面半徑， R0 為缺口半徑。但由于變形過程中缺口半徑的變化，尤其是試樣發生頸縮后，式（12） 的計算值偏離實際值。為獲取更為合理的材料失效參數，基于LS-DYNA 建立各類試樣的有限元模型，得到試樣在變形過程中單元的失效應變及應力三軸度的變化規律。有限元模型中試樣下端表面節點固定，試樣上端表面節點施加位移邊界條件，其位移量根據試驗后試樣變形位移進行設置。由于試驗中試樣拉伸在常溫準靜態下進行，材料模型采用MJC 本構模型在常溫準靜態下的簡化形式，即H-S 硬化模型。

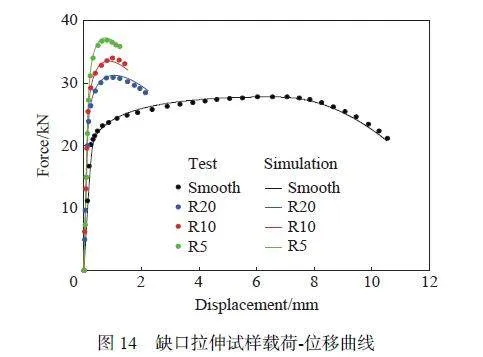
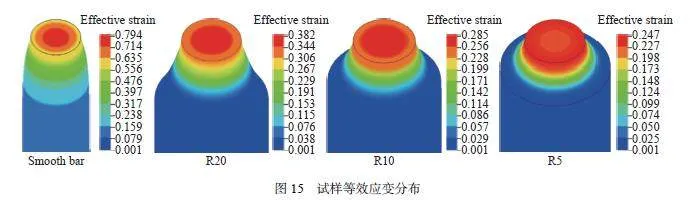
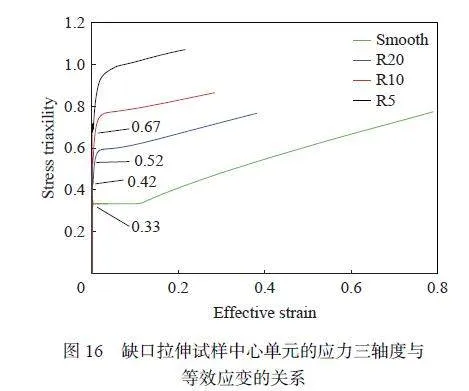
圖14 為試樣拉伸載荷-位移曲線，數值模擬和試驗曲線具有良好的一致性。從圖14 可知，材料斷裂伸長量及承受載荷顯著依賴其缺口半徑：隨試樣缺口半徑減小，斷裂伸長量顯著降低，而拉伸載荷較大程度增加。Erice 等[46] 的研究表明拉伸試樣理論上的斷裂起始點為最小截面中心單元處，中心單元具有最大的應力三軸度和較大的等效應變，提取中心單元得到應力三軸度與失效應變的關系。圖15 為拉伸試樣的等效應變分布，大應變集中在頸縮區域，其中最小截面處等效應變最大，應變呈對稱分布。光滑圓棒、R20及R10 試樣的最大等效應變單元位于截面中心，R5 試樣的最大應變單元處于截面邊緣，但最小截面上等效應變差距不大。本文提取試樣中心單元的信息，圖16 為數值模擬結果中心單元的應力三軸度與等效應變的關系，由Bridgman 公式計算的光滑圓棒、R20、R10 和R5 試樣的應力三軸度值分別為0.33、0.45、0.55 和0.74，數值模擬中在試樣初始階段與Bridgman 計算值比較相似，但由于試樣頸縮導致應力狀態變化，中心單元應力三軸度在變形過程中增大。考慮到應變的累積效應，應力三軸度取平均值：

拉伸試樣的應力三軸度和失效應變的取值見表8。

圖17 為剪切試樣斷裂狀態的試驗與數值模擬對比圖，變形區域集中在中心區域，斷裂位置出現在試樣中心處。提取斷裂截面中心單元[47] 的應力三軸度和等效應變，變化曲線如圖18 所示。在加載的初始階段試樣的應力三軸度數值在0.1 以下。隨著試樣變形，中心單元的應力三軸度呈近似線性增加。在試樣斷裂處中心單元的失效應變為0.956，平均應力三軸度為0.237。

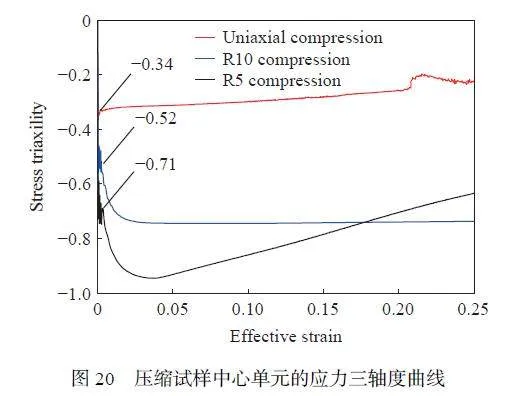
由于壓縮試驗中試樣未發生斷裂破壞（圖19），故不討論壓縮試樣的失效應變，僅確定在試樣壓縮載荷下應力三軸度的范圍，在該范圍內材料不發生斷裂失效。Bao 等[48] 的研究表明塑性金屬材料在負應力三軸度范圍內存在臨界值，當應力三軸度低于此值時，材料不會出現斷裂失效。根據Bridgman 公式[32]（壓縮狀態應力三軸度值取負）計算單軸壓縮、R10 壓縮和R5 壓縮試樣中心處的初始應力三軸度計算值分別為?0.33、?0.55 和?0.74，由理論計算值可知材料的應力三軸度臨界值大于?0.33。為進一步確定材料的應力三軸度臨界值，在數值模擬中提取壓縮試樣中心單元[33] 應力三軸度隨等效應變的變化曲線，如圖20 所示，壓縮初始階段的應力三軸度與Bridgman 公式[32] 計算值接近，單軸壓縮試樣變形后應力三軸度隨等效應變緩慢上升。根據單軸壓縮試樣中心單元的應力三軸度的變化歷程，取該過程應力三軸度的平均值為ZL114A 鋁合金的應力三軸度臨界值，數值為?0.28。

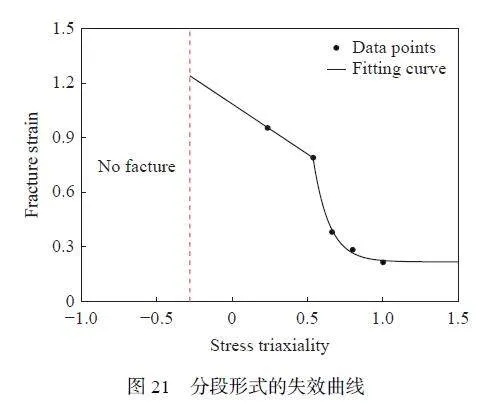
圖21 為分段形式的ZL114A 鋁合金的斷裂曲線，應力三軸度值小于?0.28 時不考慮塑性應變的累積，材料不失效；應力三軸度為?0.28～0.538 時，引入剪切試樣斷裂時的應力三軸度和失效應變，結合光滑圓棒試樣的失效應變和應力三軸度，表達式為線性函數；應力三軸度大于0.538 時，采用原始的J-C 失效準則形式。包含應力三軸度的分段形式J-C 失效準則表達式為

式中參數取值見表9。

4.2.2 溫度及應變率對失效應變的影響

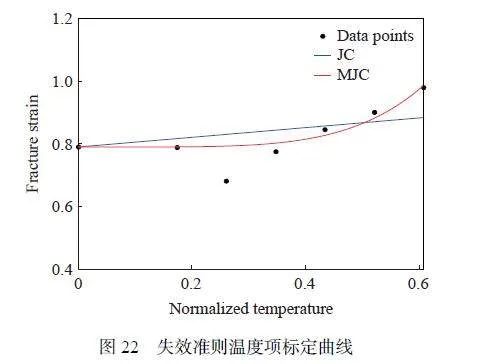
通過分步擬合方法，標定J-C 失效準則的溫度項系數。基于不同溫度下的光滑圓棒拉伸試樣數據（圖11），取試樣最小截面中心單元失效應變，得到歸一化溫度與失效應變的關系。采用J-C 失效準則的溫度項對數據進行擬合，如圖22 所示。由于J-C 失效準則的溫度項將歸一化溫度與失效應變視為線性關系，對試樣數據擬合效果欠佳，因此對J-C 失效準則溫度項進行修正，修正形式[47] 為：

εf（T*） = εf1（1+D6T*D7）（15）

式中：εf1 為常溫下光滑圓棒拉伸試樣的失效應變，其他參數取值見表9。修正后的J-C 失效準則（MJC）溫度項與失效應變的關系擬合曲線如圖22 所示。

失效應變的影響因素中，應力三軸度項最為顯著，而應變率項和溫度項影響較小[21]。由于試驗條件的限制，未開展應變率對材料失效應變的影響研究，應變項系數參考相關文獻中多數鋁合金J-C失效準則參數[13，16，22，49]，取值為0.01。考慮溫度和應變率影響的分段形式J-C 失效準為

式中參數取值見表9。

4.3 失效準則準確性驗證

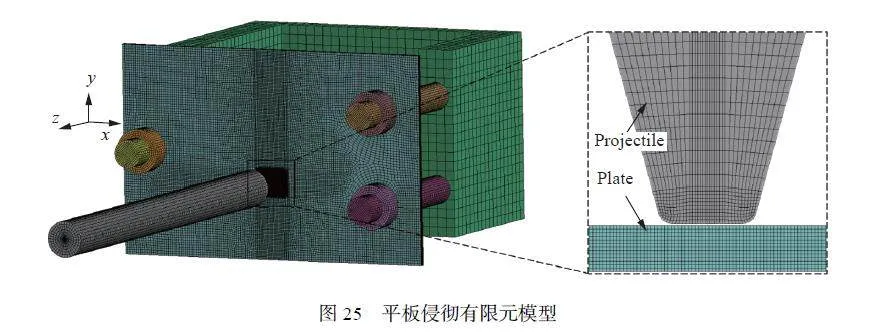
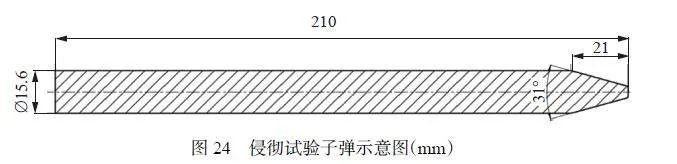
為驗證失效準則參數的準確性，開展ZL114A 鋁合金平板侵徹試驗及數值模擬。平板侵徹試驗裝置基于SHPB 試驗臺搭建，如圖23 所示。測試靶板為140 mm×70 mm×2 mm 的矩形板，采用螺栓將其固定。通過粘貼于靶板上的應變片（分別記為SG-1、SG-2、SG-3 和SG-4）記錄常溫侵徹過程的應變信號，信號采集裝置為Synergy 數據采集儀。子彈材料為40Cr 鋼，其形狀及尺寸如圖24 所示。子彈速度通過氣壓控制，試驗時氣壓設置為0.35 MPa，根據設備氣壓與子彈尺寸標定關系，子彈速度為25 m/s。加熱條件下平板侵徹試驗保持發射氣壓同常溫一致，通過控制加熱爐使平板處于不同溫度。

采用LS-DYNA 建立與平板侵徹試驗相對應的有限元模型，單元類型為六面體單點積分單元，模型單元數量為374 591，有限元模型如圖25 所示。靶體撞擊區域單元細化，參考文獻[47] 中2 mm 薄板有限元模型，細化單元的尺寸為0.15 mm×0.15 mm×0.15 mm。子彈及固定裝置為鋼制材料，試驗后未發生明顯變形，在計算模型中將其設置為剛體，密度為7 800 kg/m3，彈性模量為210 GPa，泊松比為0.33。子彈與靶體接觸設置為侵蝕接觸，其余部分與靶體接觸類型為面面接觸。接觸算法采用對稱罰函數法，接觸剛度罰因子設置為1。物體接觸考慮摩擦效應，靜摩擦因數為0.15，動摩擦因數為0.1。固定裝置背面節點設置為固定邊界條件，子彈初始速度設置為沿z 軸負方向，大小為25 m/s。在侵徹過程中考慮塑性變形引起的絕熱溫升，ZL114A 鋁合金密度ρ=2 700 kg/m3，參考文獻[27] 取比熱 =963 J/（kg?℃），取塑性功轉換系數χ=0.9，絕熱溫升表達式[49] 為：

將MJC 本構模型與分段形式的J-C 失效準則通過材料模型二次開發技術嵌入至LS-DYNA 求解器進行計算。

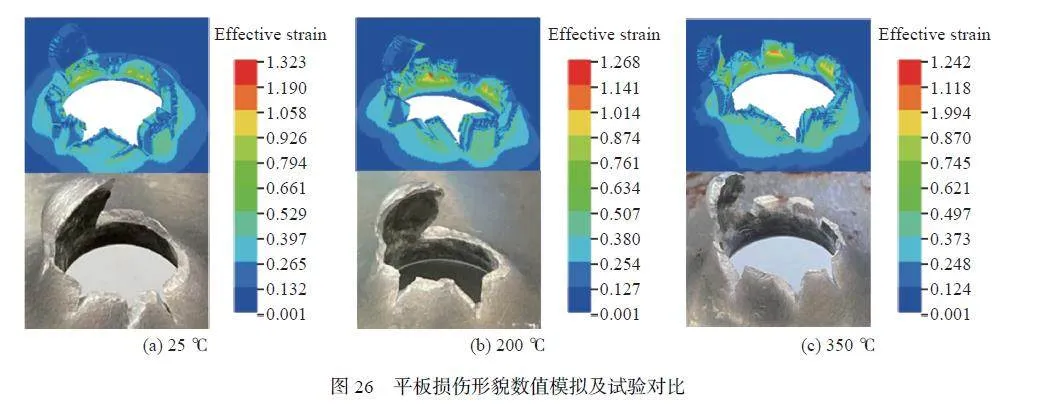
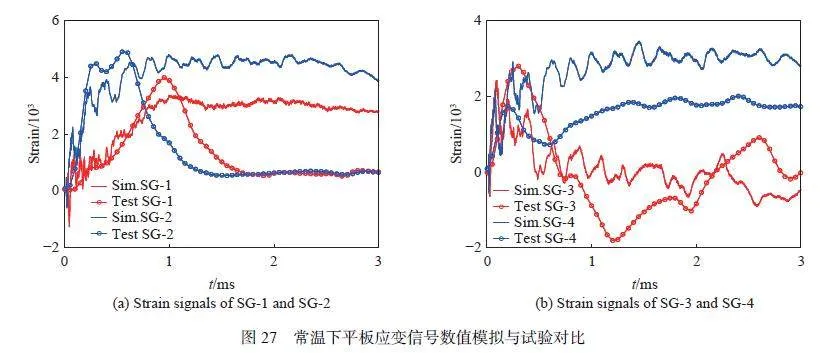
圖26 為不同溫度下平板侵徹數值模擬及試驗損傷形貌對比，數值模擬中平板損傷形貌呈花瓣型裂口，與試驗結果基本一致，多處特征比較相似，說明本文構建并標定的材料模型具有預測不同溫度下ZL114A 鋁合金失效行為的能力。圖27 為常溫下平板特定位置（圖23）數值模擬及試驗的應變信號對比，整體上數值模擬與試驗的應變數據相似性較高。SG-1、SG-2 峰值應變與試驗較為接近，由于在撞擊過程中SG-1、SG-2 應變片粘貼處發生折彎導致應變片脫落，后續應變信號誤差較大。子彈侵徹平板過程具有一定的復雜性，受多種因素影響（撞擊位置、撞擊角度、固定方式、應變片粘貼角度等偏差），SG-3、SG-4 數值模擬與試驗的應變在數值上存在差距，但SG-3、SG-4 數值模擬與試驗的應變具有相似的變化趨勢，進一步驗證了材料模型具有一定的準確性。

5 結 論

以航空發動機機匣常用材料ZL114A 鋁合金為研究對象，采用試驗與數值模擬相結合的方法，構建描述該材料在較大溫度范圍下大變形及失效行為的材料模型，為ZL114A 鋁合金結構強度研究提供理論基礎，主要結論如下：

（1） ZL114A 鋁合金具有溫度軟化效應，在125～225 ℃ 范圍內，初始屈服應力及塑性流動應力變化較小，275 ℃ 后，溫度軟化效應十分明顯，流動應力大幅度降低；應變率強化效應在1 310 s?1 時不明顯，在2 212～5 964 s?1，高應變率下的流動應力高于準靜態，但不隨應變率增大而單調提高；

（2） 有限元反求的硬化模型參數標定方法能充分利用試樣載荷-位移數據，該方法獲取的材料硬化參數描述材料大變形下的力學行為具有較高的精度；基于Hockett/Sherby 硬化模型和Cowper-Symonds 應變率項構建的本構關系可以描述ZL114A 鋁合金在大應變、寬溫度范圍下的力學行為，整體上能描述高應變率下材料的流動應力；

（3） ZL114A 鋁合金具有較好的塑性變形能力，在壓縮載荷下很難發生斷裂失效；通過數值模擬與試驗相結合的方法獲取失效參數，標定分段形式的J-C 失效準則，多種溫度下的平板侵徹試驗表明本文中的材料模型在一定程度上具有預測不同溫度下ZL114A 鋁合金失效行為的能力。

參考文獻：

[1]宣海軍， 陸曉， 洪偉榮， 等. 航空發動機機匣包容性研究綜述 [J]. 航空動力學報， 2010， 25（8）： 1860–1870. DOI：10.13224/j.cnki.jasp.2010.08.012.

XUAN H J， LU X， HONG W R， et al. Review of aero-engine case containment research [J]. Journal of Aerospace Power，2010， 25（8）： 1860–1870. DOI： 10.13224/j.cnki.jasp.2010.08.012.

[2] 中國民用航空局. 航空發動機適航規定： CCAR 33-R2 [S]. 北京： 中國民用航空局， 2011： 48–49.

[3]袁康博， 姚小虎， 王瑞豐， 等. 金屬材料的率-溫耦合響應與動態本構關系綜述 [J]. 爆炸與沖擊， 2022， 42（9）： 091401. DOI：10.11883/bzycj-2021-0416.

YUAN K B， YAO X H， WANG R F， et al. A review on rate-temperature coupling response and dynamic constitutive relation"of metallic materials [J]. Explosion and Shock Waves， 2022， 42（9）： 091401. DOI： 10.11883/bzycj-2021-0416.

[4]閆洪霞. 基于位錯物理的金屬塑性變形本構關系的研究 [D]. 杭州： 浙江大學， 2011： 4–7.

YAN H X. Study on the dislocation-based physical constitutive relations of plastic deformation of metals [D]. Hangzhou：Zhejiang University， 2011： 4–7.

[5]ZERILLI F J， ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J].Journal of Applied Physics， 1987， 61（5）： 1816–1825. DOI： 10.1063/1.338024.

[6]JOHNSON G R， COOK W H. A constitutive model and data for metals subjected to large strains， high strain rates and high"temperatures [C]//Proceedings of the 7th International Symposium on Ballistics. The Hague， Netherland， 1983： 541–547.

[7]FIELDS D S， BACKOFEN W A. Determination of strain hardening characteristics by torsion testing [J]. Proceedings"American Society for Testing and Materials， 1957， 57： 1259–1272.

[8]KHAN A S， HUANG S J. Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10?5?104 s?1 [J]. International Journal of Plasticity， 1992， 8（4）： 397–424. DOI： 10.1016/0749-6419（92）90057-J.

[9]JOHNSON G R， HOLMQUIST T J. Evaluation of cylinder-impact test data for constitutive model constants [J]. Journal of"Applied Physics， 1988， 64（8）： 3901–3910. DOI： 10.1063/1.341344.

[10]CLAUSEN A H， B?RVIK T， HOPPERSTAD O S， et al. Flow and fracture characteristics of aluminium alloy AA5083-H116"as function of strain rate， temperature and triaxiality [J]. Materials Science and Engineering： A， 2004， 364（1/2）： 260–272. DOI：10.1016/j.msea.2003.08.027.

[11]B?RVIK T， CLAUSEN A H， ERIKSSON M， et al. Experimental and numerical study on the perforation of AA6005-T6"panels [J]. International Journal of Impact Engineering， 2005， 32（1）： 35–64. DOI： 10.1016/j.ijimpeng.2005.05.001.

[12] 辛春亮， 薛再清， 涂建， 等. 有限元分析常用材料參數手冊 [M]. 北京： 機械工業出版社， 2020.

[13]鄧云飛， 張永， 吳華鵬， 等. 6061-T651 鋁合金動態力學性能及J-C 本構模型的修正 [J]. 機械工程學報， 2020， 56（20）：74–81. DOI： 10.3901/JME.2020.20.074.

DENG Y F， ZHANG Y， WU H P， et al. Dynamic mechanical properties and modification of J-C constitutive model of 6061-T651 aluminum alloy [J]. Journal of Mechanical Engineering， 2020， 56（20）： 74–81. DOI： 10.3901/JME.2020.20.074.

[14]安劍， 李永豐， 張云光， 等. 熱沖壓條件下2219 鋁合金的本構行為測試與建模 [J]. 機械工程學報， 2021， 57（4）： 44–52.DOI： 10.3901/JME.2021.04.044.

AN J， LI Y F， ZHANG Y G， et al. Constitutive behavior of 2219 aluminum alloy under hot stamping condition [J]. Journal of"Mechanical Engineering， 2021， 57（4）： 44–52. DOI： 10.3901/JME.2021.04.044.

[15]ZHANG Q D， CAO Q， ZHANG X F. A modified Johnson-Cook model for advanced high-strength steels over a wide range of"temperatures [J]. Journal of Materials Engineering and Performance， 2014， 23（12）： 4336–4341. DOI： 10.1007/s11665-014-1236-9.

[16]周倫， 蘇興亞， 敬霖， 等. 6061-T6 鋁合金動態拉伸本構關系及失效行為 [J]. 爆炸與沖擊， 2022， 42（9）： 091407. DOI： 10.11883/bzycj-2022-0154.

ZHOU L， SU X Y， JING L， et al. Dynamic tensile constitutive relationship and failure behavior of 6061-T6 aluminum alloy [J].Explosion and Shock Waves， 2022， 42（9）： 091407. DOI： 10.11883/bzycj-2022-0154.

[17]田憲華， 閆奎呈， 趙軍， 等. GH2132 高溫高應變率下力學性能分析與Johnson-Cook 本構模型的建立 [J]. 中國機械工程，2022， 33（7）： 872–881. DOI： 10.3969/j.issn.1004-132X.2022.07.015.

TIAN X H， YAN K C， ZHAO J， et al. Properties at elevated temperature and high strain rate and establishment of Johnson-Cook constitutive model for GH2132 [J]. China Mechanical Engineering， 2022， 33（7）： 872–881. DOI： 10.3969/j.issn.1004-132X.2022.07.015.

[18]滑勇之， 關立文， 劉辛軍， 等. 鋁合金7050-T7451 高溫高應變率本構方程及修正 [J]. 材料工程， 2012（12）： 7–13.

HUA Y Z， GUAN L W， LIU X J， et al. Research and revise on constitutive equation of 7050-T7451 aluminum alloy in high"strain rate and high temperature condition [J]. Journal of Materials Engineering， 2012（12）： 7–13.

[19]溫彤， 火小暢， 方剛， 等. 基于有限元逆向優化法識別22MnB5 板硬化模型參數 [J]. 天津大學學報（自然科學與工程技術版）， 2019， 52（11）： 1129–1135. DOI： 10.11784/tdxbz201812037.

WEN T， HUO X C， FANG G， et al. Identification of hardening model parameters of a 22MnB5 plate based on finite element"reverse optimization method [J]. Journal of Tianjin University （Science and Technology）， 2019， 52（11）： 1129–1135. DOI：10.11784/tdxbz201812037.

[20]茹一帆， 張樂樂， 劉文， 等. 基于缺口試件應力狀態試驗的Johnson-Cook 模型參數反演標定方法 [J]. 機械工程學報， 2021，57（22）： 60–70. DOI： 10.3901/JME.2021.22.060.

RU Y F， ZHANG L L， LIU W， et al. Inverse determination method of Johnson-Cook model parameters based on the stress"state test of notched specimens [J]. Journal of Mechanical Engineering， 2021， 57（22）： 60–70. DOI： 10.3901/JME.2021.22.060.

[21]JOHNSON G R， COOK W H. Fracture characteristics of three metals subjected to various strains， strain rates， temperatures"and pressures [J]. Engineering Fracture Mechanics， 1985， 21（1）： 31–48. DOI： 10.1016/0013-7944（85）90052-9.

[22]高玉龍， 孫曉紅. 高速列車用6008 鋁合金動態變形本構與損傷模型參數研究 [J]. 爆炸與沖擊， 2021， 41（3）： 033101. DOI：10.11883/bzycj-2020-0119.

GAO Y L， SUN X H. On the parameters of dynamic deformation and damage models of aluminum alloy 6008-T4 used for"high-speed railway vehicles [J]. Explosion and Shock Waves， 2021， 41（3）： 033101. DOI： 10.11883/bzycj-2020-0119.

[23]馬銘輝， 余毅磊， 蔣招繡， 等. 675 裝甲鋼的靜動態力學行為與J-C 模型參數擬合確定 [J]. 北京理工大學學報， 2022，42（6）： 596–603. DOI： 10.15918/j.tbit1001-0645.2021.149.

MA M H， YU Y L， JIANG Z X， et al. Static and dynamic mechanical properties of 675 armor steel and determination of J-C"model parameters [J]. Transactions of Beijing Institute of Technology， 2022， 42（6）： 596–603. DOI： 10.15918/j.tbit1001-0645.2021.149.

[24]BAO Y B， WIERZBICKI T. A comparative study on various ductile crack formation criteria [J]. Journal of Engineering"Materials and Technology， 2004， 126（3）： 314–324. DOI： 10.1115/1.1755244.

[25]TENG X， WIERZBICKI T. Evaluation of six fracture models in high velocity perforation [J]. Engineering Fracture"Mechanics， 2006， 73（12）： 1653–1678. DOI： 10.1016/j.engfracmech.2006.01.009.

[26]陳星， 劉月輝. ZL114A 鋁合金主機匣振動開裂失效分析 [J]. 理化檢驗：物理分冊， 2013， 49（10）： 697–700， 703.

CHEN X， LIU Y H. Failure analysis on fracture of ZL114A core box in vibrant testing [J]. Physical Testing and Chemical"Analysis （Part A： Physical Testing）， 2013， 49（10）： 697–700， 703.

[27]《中國航空材料手冊》編輯委員會. 中國航空材料手冊第3 卷： 鋁合金 鎂合金 [M]. 2 版. 北京： 中國標準出版社， 2002：399–400.

[28] 陳光， 洪杰， 馬艷紅. 航空燃氣渦輪發動機結構 [M]. 北京： 北京航空航天大學出版社， 2010： 91–92.

[29]康福偉， 張繼敏， 樊德智， 等. ZL114A 合金熱變形本構方程 [J]. 哈爾濱理工大學學報， 2018， 23（2）： 134–139. DOI：10.15938/j.jhust.2018.02.024.

KANG F W， ZHANG J M， FAN D Z， et al. Constitutive equation of hot deformation of ZL114A alloy [J]. Journal of Harbin"University of Science and Technology， 2018， 23（2）： 134–139. DOI： 10.15938/j.jhust.2018.02.024.

[30]王伏林， 孫興祚， 肖強， 等. ZL114A 鋁合金高應變速率下的本構模型與損傷模型 [J]. 塑性工程學報， 2022， 29（11）：120–126. DOI： 10.3969/j.issn.1007-2012.2022.11.014.

WANG F L， SUN X Z， XIAO Q， et al. Constitutive model and damage model of ZL114A aluminum alloy with high strain rate [J].Journal of Plasticity Engineering， 2022， 29（11）： 120–126. DOI： 10.3969/j.issn.1007-2012.2022.11.014.

[31]葉拓， 李落星， 郭鵬程， 等. 6063 鋁合金在沖擊載荷下的尺寸效應及數值模擬 [J]. 中國機械工程， 2016， 27（23）： 3229–3234. DOI： 10.3969/j.issn.1004-132X.2016.23.017.

YE T， LI L X， GUO P C， et al. Effect of specimen size at impact load of 6063 aluminum alloy and numerical simulation [J].China Mechanical Engineering， 2016， 27（23）： 3229–3234. DOI： 10.3969/j.issn.1004-132X.2016.23.017.

[32]BRIDGMAN W P. Studies in large plastic flow and fracture： with special emphasis on the effects of hydrostatic pressure [M].New York： McGraw-Hill， 1952.

[33]西禹， 張強， 張欣鑰， 等. 增材制造TC4 鈦合金的動態力學行為研究 [J]. 力學學報， 2022， 54（2）： 425–444. DOI： 10.6052/0459-1879-21-418.

XI Y， ZHANG Q， ZHANG X Y， et al. Dynamic mechanical behavior of additive manufacturing TC4 alloy [J]. Chinese"Journal of Theoretical and Applied Mechanics， 2022， 54（2）： 425–444. DOI： 10.6052/0459-1879-21-418.

[34]仇鵬， 王家毅， 段曉鴿， 等. AA7021 鋁合金熱變形行為及微觀組織演變機理的研究 [J]. 材料導報， 2020， 34（8）：8106–8112. DOI： 10.11896/cldb.19030088.

QIU P， WANG J Y， DUAN X G， et al. Study on hot deformation behavior and microstructure evolution mechanism of"AA7021 aluminum alloy [J]. Materials Reports， 2020， 34（8）： 8106–8112. DOI： 10.11896/cldb.19030088.

[35]蔣顯全， 蔣詩琪， 齊寶， 等. 鋁合金高低溫力學性能研究及應用前景 [J]. 世界有色金屬， 2015（10）： 20–25.

JIANG X Q， JIANG S Q， QI B， et al. The study and application prospect on low-temperature mechanical properties of"aluminium alloy [J]. World Nonferrous Metals， 2015（10）： 20–25.

[36] 胡時勝， 王禮立， 宋力， 等. Hopkinson 壓桿技術在中國的發展回顧 [J]. 爆炸與沖擊， 2014， 34（6）： 641–657. DOI：10.11883/1001-1455（2014）06-0641-17.

HU S S， WANG L L， SONG L， et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion"and Shock Waves， 2014， 34（6）： 641–657. DOI： 10.11883/1001-1455（2014）06-0641-17.

[37] 余同希， 華云龍. 結構塑性動力學引論 [M]. 合肥： 中國科學技術大學出版社， 1994： 1–2.

[38]"周古昕， 郎玉婧， 杜秀征， 等. 高強7A62 鋁合金動態力學響應及其J-C 本構關系 [J]. 中國有色金屬學報， 2021， 31（1）：21–29. DOI： 10.11817/j.ysxb.1004.0609.2021-37765.

ZHOU G X， LANG Y J， DU X Z， et al. Dynamic mechanical response and J-C constitutive equation of high strength 7A62"aluminum alloy [J]. The Chinese Journal of Nonferrous Metals， 2021， 31（1）： 21–29. DOI： 10.11817/j.ysxb.1004.0609.2021-37765.

[39]董伊康， 齊建軍， 孫力， 等. 車用鋼板材料硬化模型的適用性 [J]. 機械工程材料， 2020， 44（10）： 81–86. DOI： 10.11973/jxgccl202010017.

DONG Y K， QI J J， SUN L， et al. Applicability of hardening models for automobile steel sheets [J]. Materials for Mechanical"Engineering， 2020， 44（10）： 81–86. DOI： 10.11973/jxgccl202010017.

[40]KLEEMOLA H J， NIEMINEN M A. On the strain-hardening parameters of metals [J]. Metallurgical Transactions， 1974， 5（8）：1863–1866. DOI： 10.1007/BF02644152.

[41]HOCKETT J E， SHERBY O D. Large strain deformation of polycrystalline metals at low homologous temperatures [J].Journal of the Mechanics and Physics of Solids， 1975， 23（2）： 87–98. DOI： 10.1016/0022-5096（75）90018-6.

[42]黃志輝， 陳盛釗， 柏友運. 顯式準靜態幾種加載方法的討論 [J]. 武漢理工大學學報， 2011， 33（6）： 122–125， 129. DOI：10.3963/j.issn.1671-4431.2011.06.028.

HUANG Z H， CHEN S Z， BAI Y Y. Discussion of explicit quasi-static loading methods [J]. Journal of Wuhan University of"Technology， 2011， 33（6）： 122–125， 129. DOI： 10.3963/j.issn.1671-4431.2011.06.028.

[43]宋家慶， 陸勇， 顧歡達， 等. 彈性、彈塑性材料顯式模擬計算中的準靜態加載速度研究 [J]. 固體力學學報， 2019， 40（3）：277–286. DOI： 10.19636/j.cnki.cjsm42-1250/o3.2019.006.

SONG J Q， LU Y， GU H D， et al. Study on quasi-static loading rate in explicit calculation of elastic and elastic-plastic materials [J]. Chinese Journal of Solid Mechanics， 2019， 40（3）： 277–286. DOI： 10.19636/j.cnki.cjsm42-1250/o3.2019.006.

[44] HALLQUIST J O. LS-DYNA theory manual [M]. CA： Livermore Software Technology Corporation， 2006.

[45]COWPER G R， SYMONDS P S. Strain-hardening and strain-rate effects in the impact loading of cantilever beams [R].Providence： Brown University， 1957.

[46]ERICE B， GáLVEZ F， CENDóN D A， et al. Flow and fracture behaviour of FV535 steel at different triaxialities， strain rates"and temperatures [J]. Engineering Fracture Mechanics， 2012， 79： 1–17. DOI： 10.1016/j.engfracmech.2011.08.023.

[47]鄧云飛， 張永， 曾憲智， 等. 6061-T651 鋁合金動態力學性能及斷裂準則修正 [J]. 機械工程學報， 2020， 56（18）： 81–91. DOI：10.3901/jme.2020.18.081.

DENG Y F， ZHANG Y， ZENG X Z， et al. Dynamic mechanical properties and modification of fracture criteria of 6061-T651"aluminum alloy [J]. Journal of Mechanical Engineering， 2020， 56（18）： 81–91. DOI： 10.3901/jme.2020.18.081.

[48]BAO Y B， WIERZBICKI T. On the cut-off value of negative triaxiality for fracture [J]. Engineering Fracture Mechanics，2005， 72（7）： 1049–1069. DOI： 10.1016/j.engfracmech.2004.07.011.

[49]張偉， 魏剛， 肖新科. 2A12 鋁合金本構關系和失效模型 [J]. 兵工學報， 2013， 34（3）： 276–282. DOI： 10.3969/j.issn.1000-1093.2013.03.004.

ZHANG W， WEI G， XIAO X K. Constitutive relation and fracture criterion of 2A12 aluminum alloy [J]. Acta Armamentarii，2013， 34（3）： 276–282. DOI： 10.3969/j.issn.1000-1093.2013.03.004.

（責任編輯 王小飛）

基金項目： 湖南省自然科學基金面上項目（2020JJ4026）；湖南省研究生科研創新項目（CX20210997）