融合混沌映射和自適應T分布的蜣螂優化算法

摘要：針對原始蜣螂優化算法（DBO）存在的收斂精度低、易陷入局部最優等問題，提出一種改進的蜣螂優化算法。該算法采用混沌映射初始化蜣螂種群以提高種群的多樣性，引入北方蒼鷹優化算法的勘探策略以增強算法的全局勘探能力，并改進一種非線性邊界收斂因子以平衡其收斂速度和收斂精度。同時，采用自適應T分布擾動策略以增強算法跳出局部最優的能力。實驗結果表明，改進后的DBO算法在15個基準測試函數的求解尋優中，有13個測試函數的求解結果優于原始蜣螂優化算法、麻雀搜索算法、灰狼優化算法、鯨魚優化算法和哈里斯鷹優化算法的求解結果，表現出更高的收斂精度、更快的收斂速度及更高的穩定性。

關鍵詞：蜣螂優化算法；混沌映射；T分布擾動；基準測試函數

中圖分類號：TP181文獻標志碼：A

0引言（Introduction）

蜣螂優化算法［1］是由東華大學的沈波教授及其團隊于2022年提出的一種新型智能優化算法，該算法目前已廣泛應用于無人機路徑規劃［2］、無線傳感器網絡的節點部署［3］以及故障診斷［4］等領域。然而，DBO算法仍存在收斂精度低、易陷入局部最優等問題。針對這些問題，已有不少學者對其進行了改進研究。例如，LI等［5］提出了一種自適應步長策略和隨機差分變異策略相結合的蜣螂優化算法，增強了算法跳出局部最優的能力；郭琴等［6］提出了一種融合麻雀搜索算法追隨機制的擾動策略和柯西高斯變異的蜣螂優化算法，提高了算法的收斂速度和收斂精度；ZHU等［7］提出了一種基于量子計算和佳點集初始化的蜣螂優化算法，進一步優化了算法性能。

針對蜣螂優化算法存在的問題，本文提出了改進的蜣螂優化算法IDBO。該算法通過在種群初始化時引入piecewise映射，顯著提升了種群的多樣性。同時，通過引入北方蒼鷹優化算法的勘探策略，提高了本算法的全局搜索能力。為了進一步優化性能，本算法中設置了非線性邊界收斂因子，平衡了算法的收斂速度和收斂精度。此外，通過引入自適應T分布擾動，進一步提高了算法跳出局部最優的能力。實驗結果顯示，在15個基準測試函數的求解尋優中，本算法相較于其他算法，普遍表現出更為優越的性能。

1蜣螂優化算法（DungBeetleOptimizationalgorithm）

蜣螂優化算法是從自然界中蜣螂的5種特定行為——滾球、跳舞、繁殖、覓食和偷竊中汲取靈感而設計的一種智能優化算法。

1.1滾球行為

當在滾球的過程中沒有遇到障礙，蜣螂會利用天體進行導航，此時其位置更新公式如下：

xt+1i=xtiy1K6OcGAYVNdje1JD5vecw==+α·k·xt-1i+b·〖JB（|〗xti-xtworst〖JB）|〗[JZ）][JY]（1）

其中：t為當前迭代次數；xti表示第i只蜣螂在第t次迭代時的位置；α是值為-1或1的自然系數；k是（0，0.2）之間的常數，稱為偏轉系數；b是（0，1）之間的常數；〖JB（|〗xti-xtworst〖JB）|〗為周圍環境的變化，其中xtworst表示當前種群中最差的蜣螂位置。

1.2跳舞行為

當在滾球的過程中遇到障礙，蜣螂會通過跳舞的方式重新確定滾球方向，而跳舞行為則是通過切線函數完成的，滾球方向θ在（0，π）之間，當滾球方向重新確定后，蜣螂將繼續滾動糞球，此時其位置更新公式如下：

1.3繁殖行為

合適的產卵地點對于蜣螂繁育后代十分重要，因此蜣螂會將糞球滾到安全且適合產卵的區域，并進行隱藏。根據蜣螂的這種行為，給出一種邊界選擇策略（3）用于模擬繁殖蜣螂的產卵區域：

其中：Lb*和Ub*分別表示產卵區域的下限和上限，xtlbest為當前局部最佳位置，R=1-t/T為線性收斂因子，T為最大迭代次數，Lb和Ub分別為要優化問題的下限和上限。

當產卵區域確定后，繁殖蜣螂就會開始產卵，并且每次迭代只產出一枚卵，由公式（3）可知，產卵區域是動態變化的，因此卵的位置也是動態更新的。此時，其位置更新公式如下：

其中：Bti為第i個卵第t次迭代時的位置，[WTHX]b[WTBX]1和[WTHX]b[WTBX]2為1×D的獨立隨機向量，D表示優化問題的維度。

1.4覓食行為

當幼蟲破卵而出并成長為小蜣螂后，通常會出來覓食，根據公式（5）對其覓食區域進行限定：

其中：Lbl和Ubl為小蜣螂覓食范圍的下限和上限，xtgbest為當前全局最優位置，其位置更新公式如下：

1.5偷竊行為

在蜣螂種群中存在偷竊糞球的行為，其位置更新公式如下：

xt+1i=xtgbest+S·[WTHX]g[WTBX]·（|xti-xtlbest|+|xti-xtgbest|）[JZ）][JY]（7）

其中：S為常數，[WTHX]g[WTBX]為服從正態分布的隨機向量。

在種群中，滾球蜣螂、繁殖蜣螂、覓食蜣螂和偷竊蜣螂的比例為6∶6∶7∶11。

根據“天下沒有免費的午餐”這一普遍原理，蜣螂優化算法與其他智能優化算法一樣，都存在全局搜索與局部開發之間的不平衡、收斂精度差及易陷入局部最優的問題。為克服這些缺陷，本研究提出一種改進的蜣螂優化算法，旨在通過一系列創新策略對原有算法進行修正與優化。

2.1混沌映射

由于種群初始化是隨機的，所以容易出現種群分布不均勻的情況，導致種群的多樣性下降，進而對后續的尋優造成影響。考慮到混沌映射具有隨機性和混沌遍歷性的特性，因此常被用來代替隨機數發生器，以增加種群的多樣性。本文引入piecewise映射優化種群初始化過程，如圖1和圖2所示分別為piecewise映射分布圖和piecewise映射直方圖。

2.2引入北方蒼鷹優化算法的勘測策略

在滾球蜣螂無障礙前進階段引入北方蒼鷹優化算法［8］的勘探策略。由于在原始蜣螂優化算法中滾球蜣螂更新策略涉及的參數較多，并且各蜣螂之間相互孤立，不存在信息交流，這會導致優化算法過早收斂并陷入局部最優而無法找到全局最優解。北方蒼鷹優化算法在勘探階段對獵物的選擇是隨機的，即任意選定一個糞球并進行滾動，因此能夠克服原始蜣螂優化算法存在的缺點，增強算法全局尋優的能力；無障礙前進階段滾球蜣螂位置更新公式為

其中：xt+1i為第i只滾球蜣螂第t+1次迭代的新位置，xti為第i只滾球蜣螂第t次迭代的原位置，pi為第i只滾球蜣螂選擇的糞球的位置，r是［0，1］之間的隨機數，I為1或者2的整數，Fi為第i只滾球蜣螂位置的目標函數值，FPi為第i只滾球蜣螂選擇的糞球位置的目標函數值。

2.3非線性收斂因子

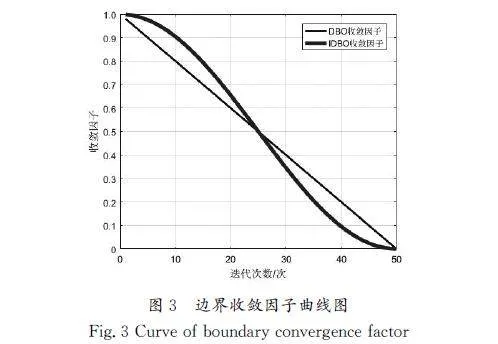
由原始蜣螂算法可知，蜣螂的繁殖和覓食行為被規定在一個動態變化的范圍內，其中線性收斂因子R=1-t/T，它雖然會隨著迭代次數的變化而動態更新，但是依然難以表征在真實的自然界中蜣螂繁殖和覓食的復雜性。此外，在迭代的前期，通常研究人員希望算法能夠對全局可行區域進行更為廣泛的搜索，而在迭代后期更加注重在最優解附近的局部開發，以加快其收斂速度。因此，提出一種余弦收斂因子重新對其范圍進行規定，公式為

DBO算法和IDBO算法的邊界收斂因子曲線圖如圖3所示，由此可知，改進后的DBO算法邊界收斂因子在迭代的前期以一個較慢的速度下降，擴大了蜣螂繁殖和覓食的范圍，提高了算法的全局探索能力，而在迭代的后期以一個較快的速度下降，加快了算法的收斂速度。

2.4引入自適應T分布擾動

為了進一步增強蜣螂優化算法在全局探索與局部開發之間的平衡能力，本文研究在小蜣螂覓食階段引入自適應T分布干擾。t（iter）為以迭代次數iter為自由度參數的T分布變異擾動，使用其對小蜣螂的覓食行為進行擾動。在迭代的開始階段，T分布擾動與柯西變異類似，這使得蜣螂算法在此時具有較強的全局探索能力；而在迭代后期，T分布擾動類似于高斯變異，此時算法的局部開發能力更為突出，同時算法的收斂速度也得以提升，新位置的更新方式如公式（10）所示：

2.5改進后的算法流程

步驟1：使用piecewise映射初始化蜣螂種群，增加種群多樣性。

步驟2：計算蜣螂種群的適應度值，更新當前最優位置。

步驟3：蜣螂在滾球無障礙前進階段使用公式（8）更新蜣螂位置，在滾球過程中遇到障礙時，使用公式（2）更新蜣螂位置。

步驟4：對于繁殖蜣螂和覓食蜣螂分別使用公式（4）和公式（10）更新蜣螂位置。

步驟5：對于偷竊蜣螂使用公式（7）更新蜣螂位置。

步驟6：對每只蜣螂進行邊界判定，更新計算當前適應度值及最優值。

步驟7：判定t是否為最大迭代次數，若是，則停止更新；反之，返回“步驟3”繼續執行。

3基準測試函數（Benchmarktestfunction）

3.1實驗設置

本文選取CEC2005基準測試函數中的15個函數進行性能測試，其中F1～F7為單峰測試函數，其有且只有一個最優解，可以使用其對算法的局部開發性能進行檢驗；F8～F13為多峰測試函數，與單峰測試函數不同，多峰測試函數除了有一個全局最優解，還存在多個局部最優解。此時，大多算法往往會陷入局部最優而無法找到全局最優解，因此可以用來測試算法的全局探索能力；F14、F15為固定多峰測試函數。基準測試函數如表1所示。

3.2實驗結果

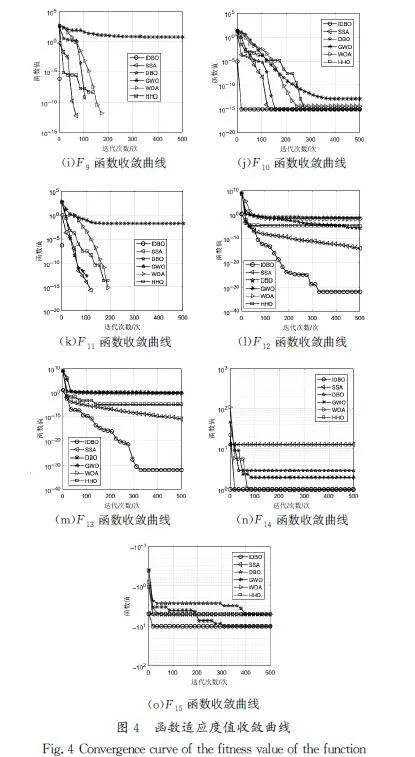
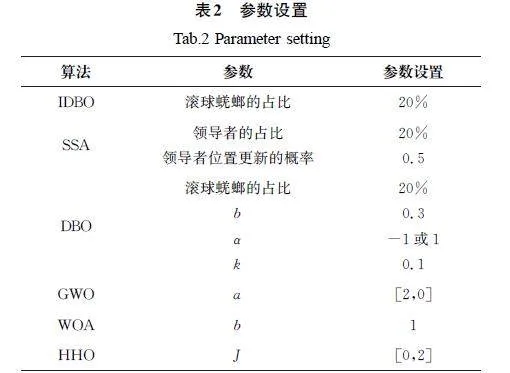
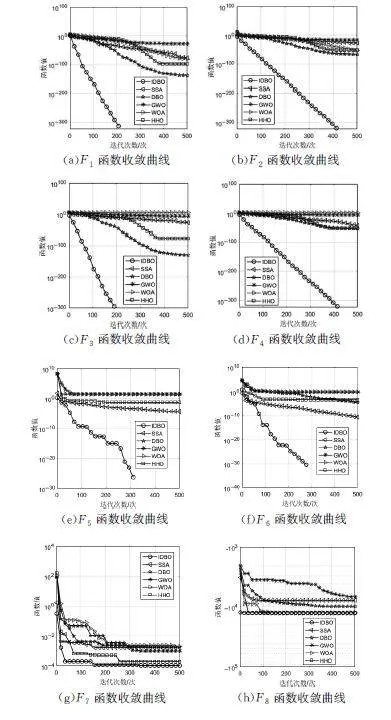
在本次實驗中，所有算法的種群規模均設置為30，最大迭代次數設置為500次，為防止單次實驗存在偶然性，將各算法均獨立運行30次，然后取其最優值、標準差和平均值作為算法性能好壞的最終評定標準，其中最優值和平均值可以表征算法的收斂精度，標準差可以表征算法的穩定性。各算法性能的對比結果如表3所示（加粗部分表示各種算法的最優值），同時繪制算法的適應度收斂曲線圖（圖4），從中可以看出，改進后蜣螂優化算法的性能普遍優于其他對比算法的性能。

由表3可知，對于單峰測試函數F1～F7，由F1～F4和F6的最優值、標準差、平均值表明，IDBO算法的表現均優于其他算法，且這5個函數均能穩定地收斂到其最優解，而對于F5和F7，IDBO算法的性能雖然不是最好，但其各項指標均排在各算法的前列，并且F5的最優值得到了理論最優值。對于多峰測試函數F8～F13，IDBO算法的最優值、標準差、平均值相較于其他算法都表現為最小或者并列最小，其中F8、F9、F11達到了其理論最優值。對于固定多峰測試函數F14、F15，各種算法基本都能尋找到其最優值，但IDBO算法的標準差和平均值明顯優于其他算法的相應指標值。綜合來看，采用IDBO算法對15個基準測試函數進行求解尋優，其中有13個測試函數的求解結果優于其他各種對比算法的求解結果。通過上述分析可以看出，無論是對于單峰測試函數還是多峰測試函數，IDBO算法的大部分最優值和平均值都要優于其他對比算法的相應指標值，并且其標準差普遍小于其他算法。這表明經改進后的蜣螂優化算法較其他優化算法有著更高的尋優精度和穩定性。

從圖4的數據分析中可以觀察到，相較于其他對比算法，IDBO算法在大部分的基準測試函數上均展現出了優越的性能，具體表現為更快的收斂速度與更高的收斂精度。無論是對于單峰測試函數還是多峰測試函數，IDBO算法均能保持出色的表現，這說明改進后的蜣螂優化算法不僅能夠快速收斂，還能夠對函數解進行進一步的開發，即IDBO算法在全局探索能力與局部尋優能力之間找到了合理的平衡。

4結論（Conclusion）

針對蜣螂優化算法存在的收斂精度低、易陷入局部最優等問題，提出了一種改進的蜣螂優化算法，即IDBO算法。首先，在初始化種群階段引入piecewise映射，增加其種群多樣性；其次，在蜣螂滾球的無障礙前進階段引入北方蒼鷹優化算法的勘探策略，利用其對食物選擇的隨機性增強算法的全局勘探能力；再次，對蜣螂繁殖和覓食的邊界收斂因子進行改進，使其收斂精度和收斂速度得到平衡；最后，在蜣螂覓食階段引入自適應T分布擾動，進一步增強算法跳出局部最優的能力。通過在CEC2005基準測試函數集的15個函數上進行驗證，IDBO算法相較于其他對比算法，展現出了最高的收斂精度、更快的收斂速度及更高的穩定性。

參考文獻（References）

［1］XUEJK，SHENB.Dungbeetleoptimizer：anewmeta＼|heuristicalgorithmforglobaloptimization［J］.TheJournalofsupercomputing，2023，79（7）：7305＼|7336.

［2］遠翔宇，楊風暴，楊童瑤.基于自適應蜣螂算法的無人機三維路徑規劃方法［J］.無線電工程，2024，54（4）：928＼|936.

［3］付雷，王驥.基于改進蜣螂優化算法的海洋牧場三維UWSN覆蓋方法［J］.中山大學學報（自然科學版），2024，63（2）：115＼|122.

［4］趙鑫，王東麗，彭泓，等.基于多策略改進蜣螂算法優化的變壓器故障診斷［J］.電力系統保護與控制，2024，52（6）：120＼|130.

［5］LIYH，SUNKX，YAOQ，etal.Adual＼|optimizationwindspeedforecastingmodelbasedondeeplearningandimproveddungbeetleoptimizationalgorithm［J］.Energy，2024，286：129604.

［6］郭琴，鄭巧仙.多策略改進的蜣螂優化算法及其應用［J］.計算機科學與探索，2024，18（4）：930＼|946.

［7］ZHUF，LIGS，TANGH，etal.Dungbeetleoptimizationalgorithmbasedonquantumcomputingandmulti＼|strategyfusionforsolvingengineeringproblems［J］.Expertsystemswithapplications，2024，236：121219.

［8］DEHGHANIM，HUBLOVSKYS，TROJOVSKYP.Northerngoshawkoptimization：anewswarm＼|basedalgorithmforsolvingoptimizationproblems［J］.IEEEaccess，2021，9：162059＼|162080.

［9］XUEJK，SHENB.Anovelswarmintelligenceoptimizationapproach：sparrowsearchalgorithm［J］.Systemsscience&controlengineering，2020，8（1）：22＼|34.

［10］MIRJALILIS，MIRJALILISM，LEWISA.Greywolfoptimizer［J］.Advancesinengineeringsoftware，2014，69：46＼|61.

［11］MIRJALILIS，LEWISA.Thewhaleoptimizationalgorithm［J］.Advancesinengineeringsoftware，2016，95（C）：51＼|67.

［12］HEIDARIAA，MIRJALILIS，FARISH，etal.HarrisHawksoptimization：algorithmandapplications［J］.Futuregenerationcomputersystems，2019，97：849＼|872.