基于可達陣的多級評分最簡完備Q矩陣設計

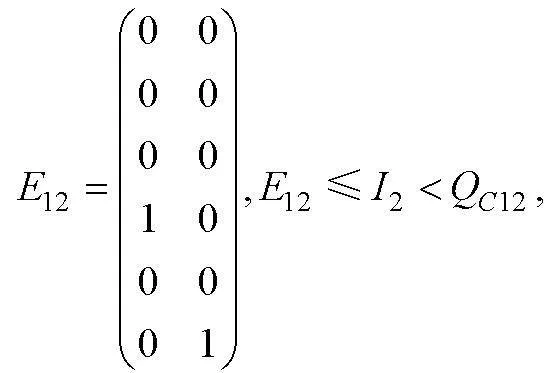
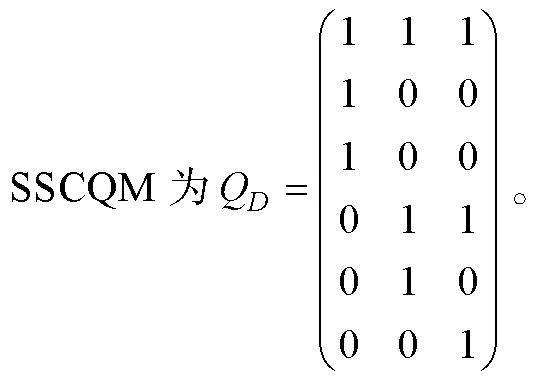
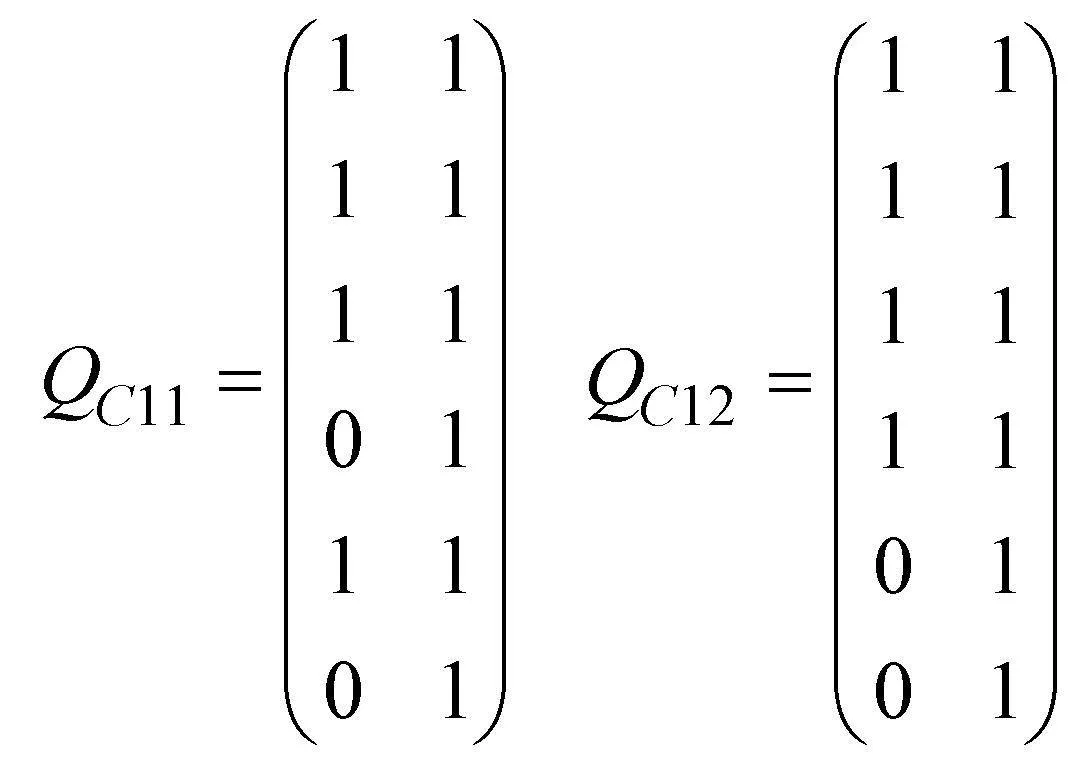
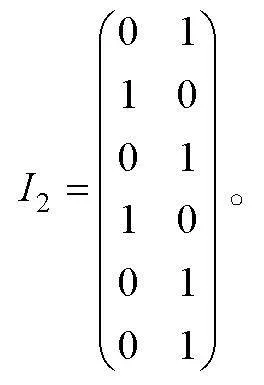
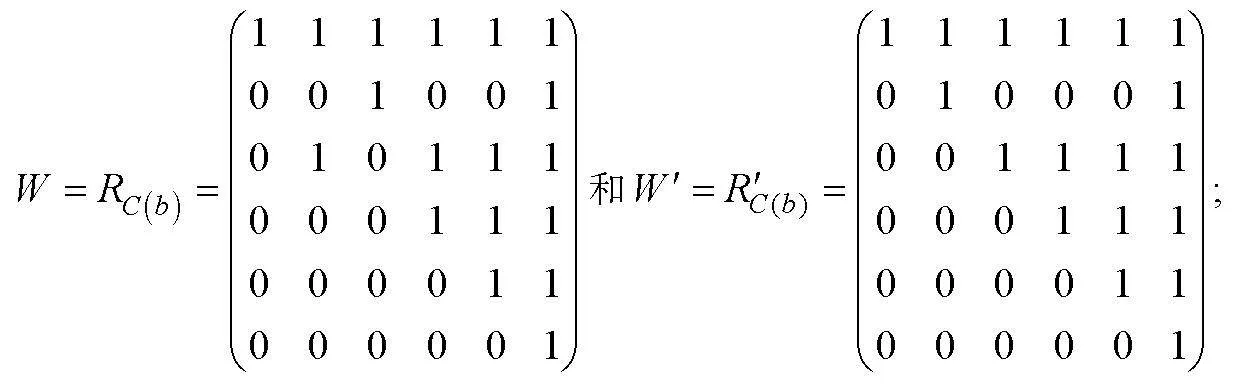
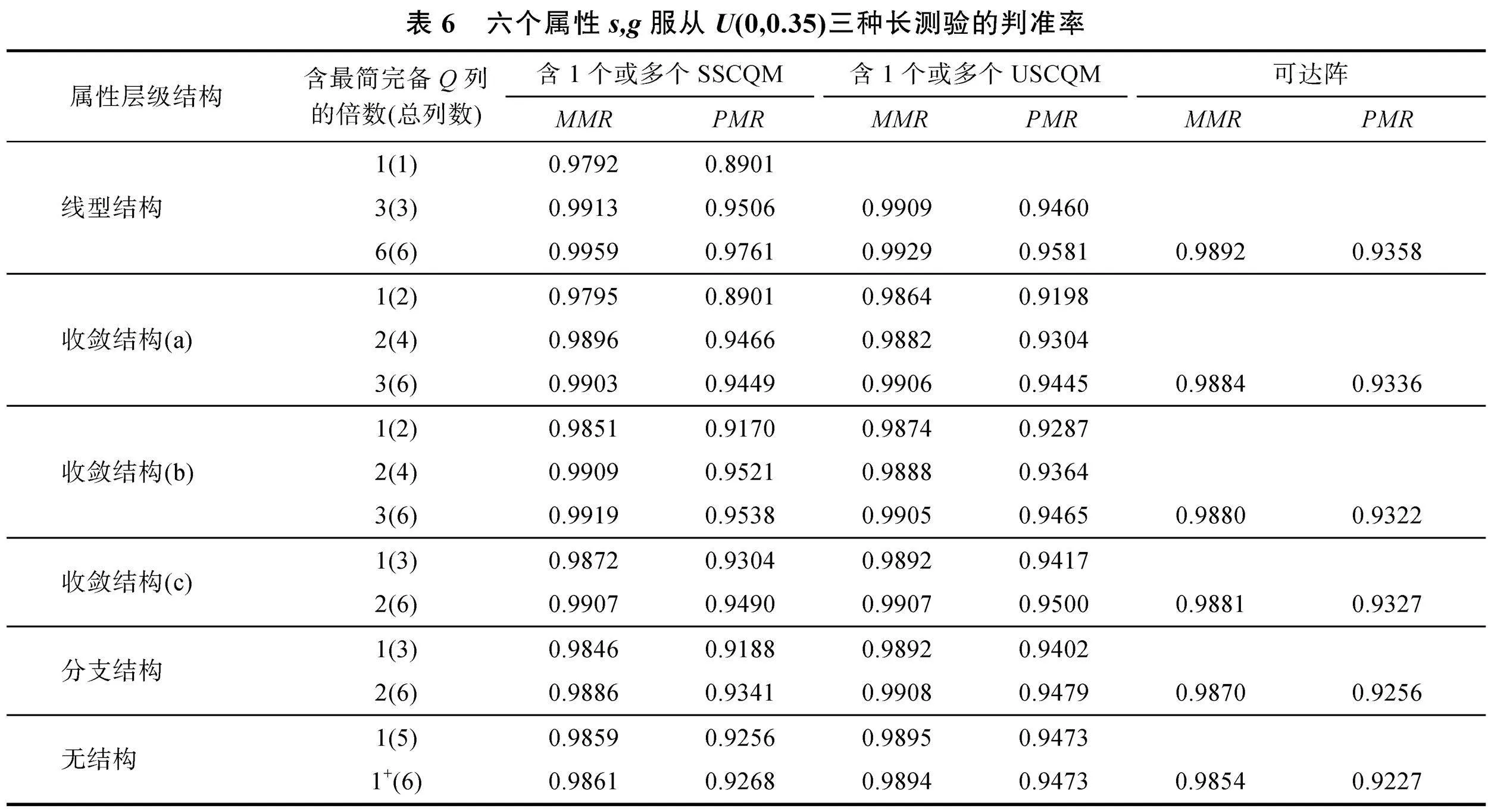
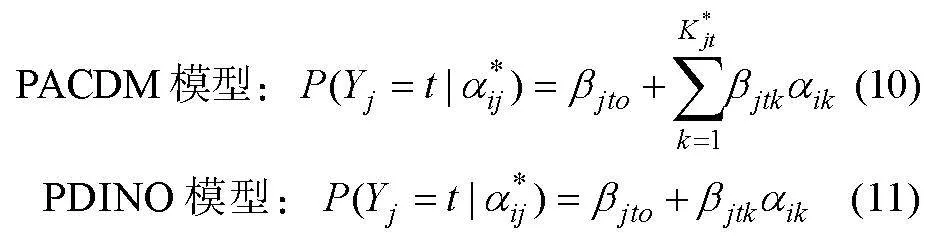
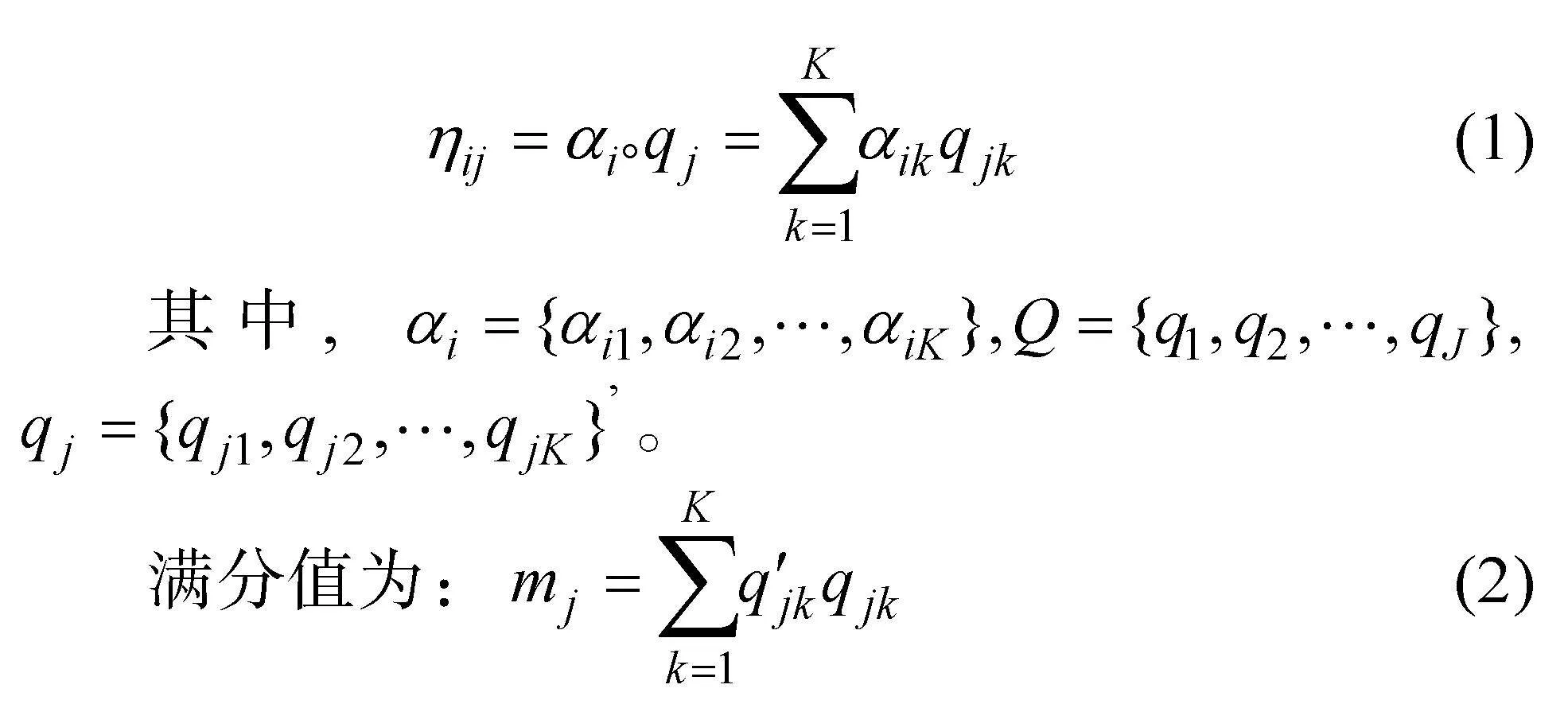
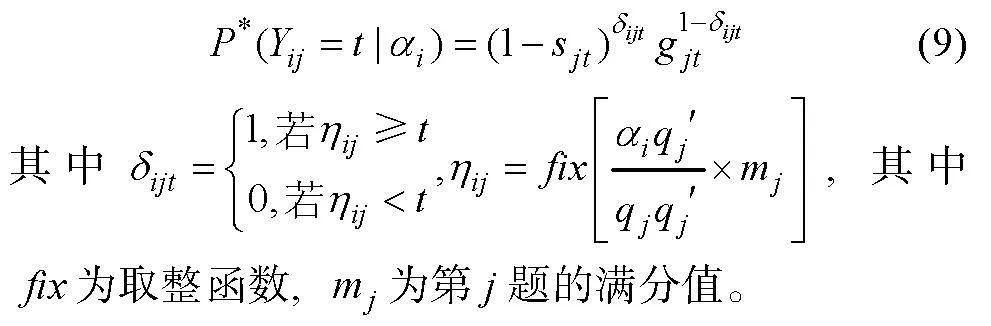
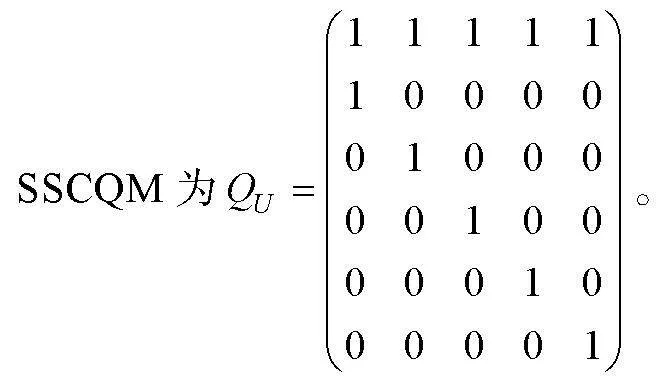
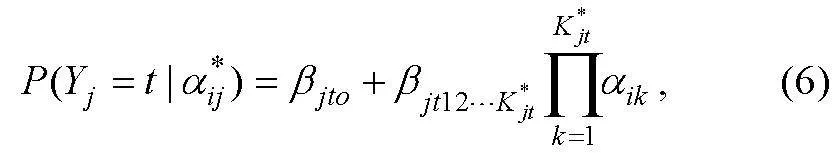
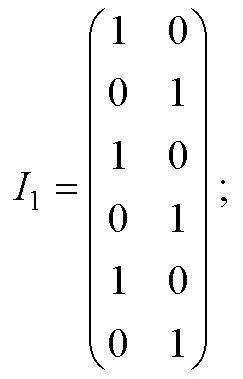
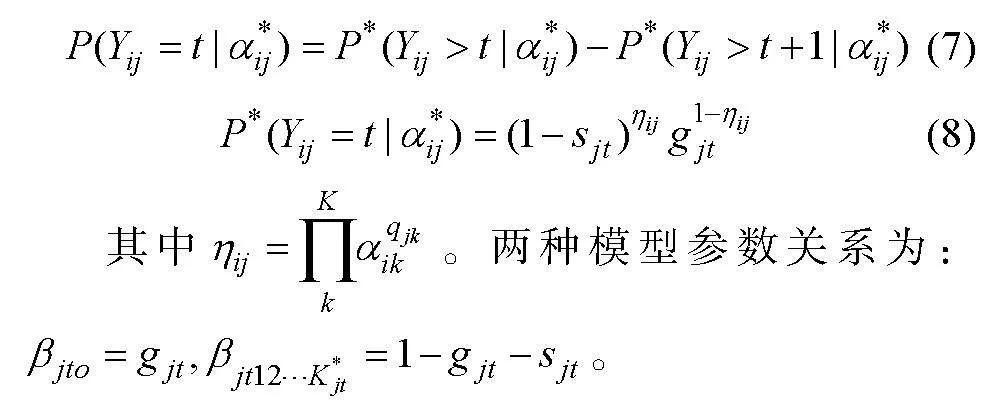
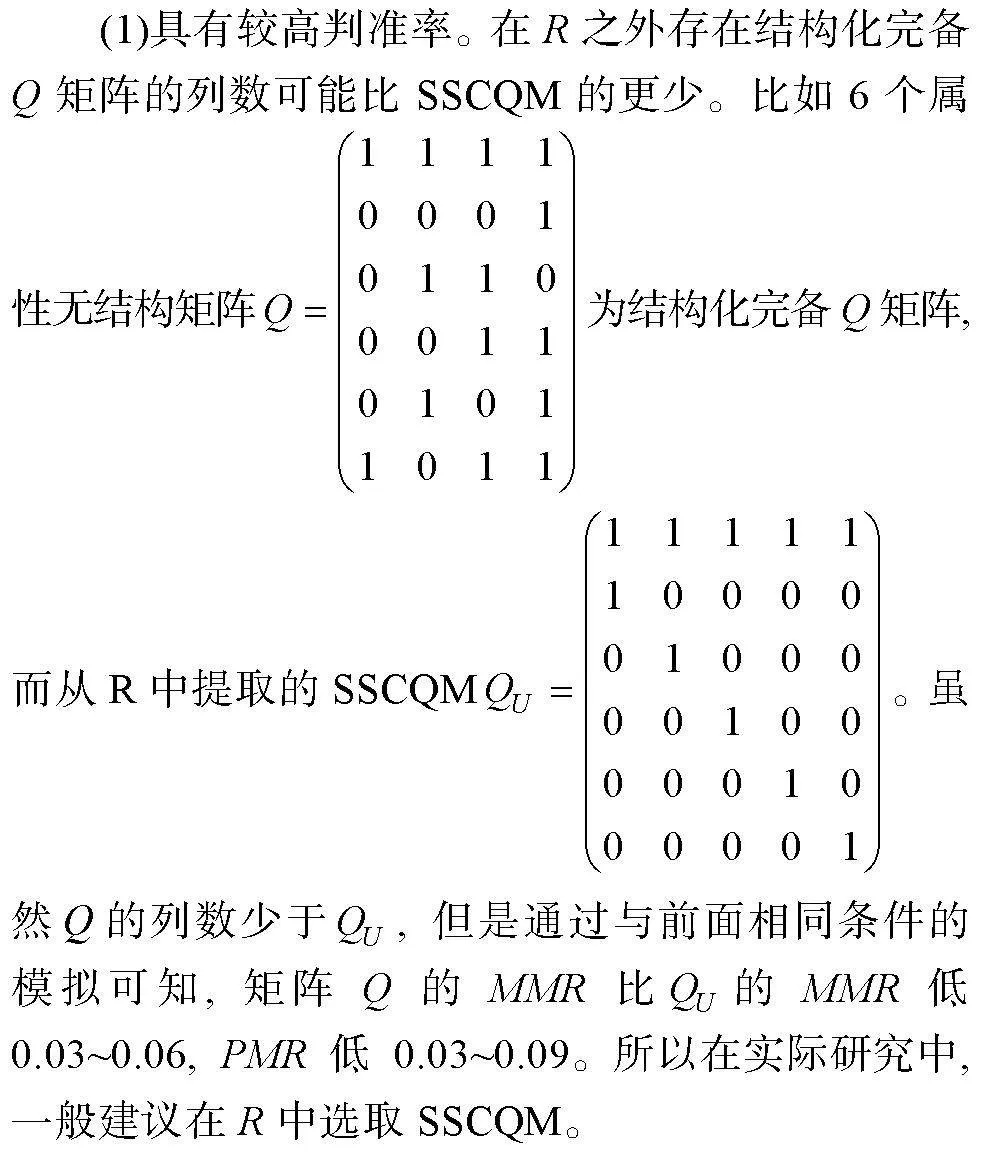
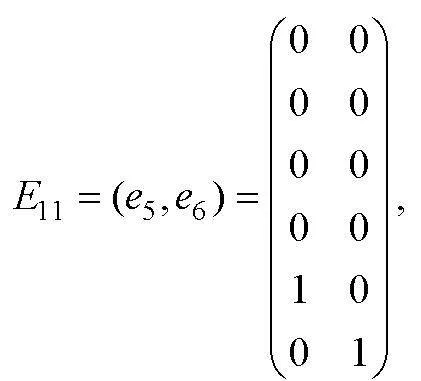
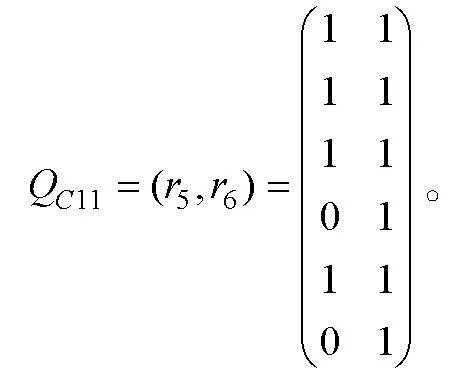
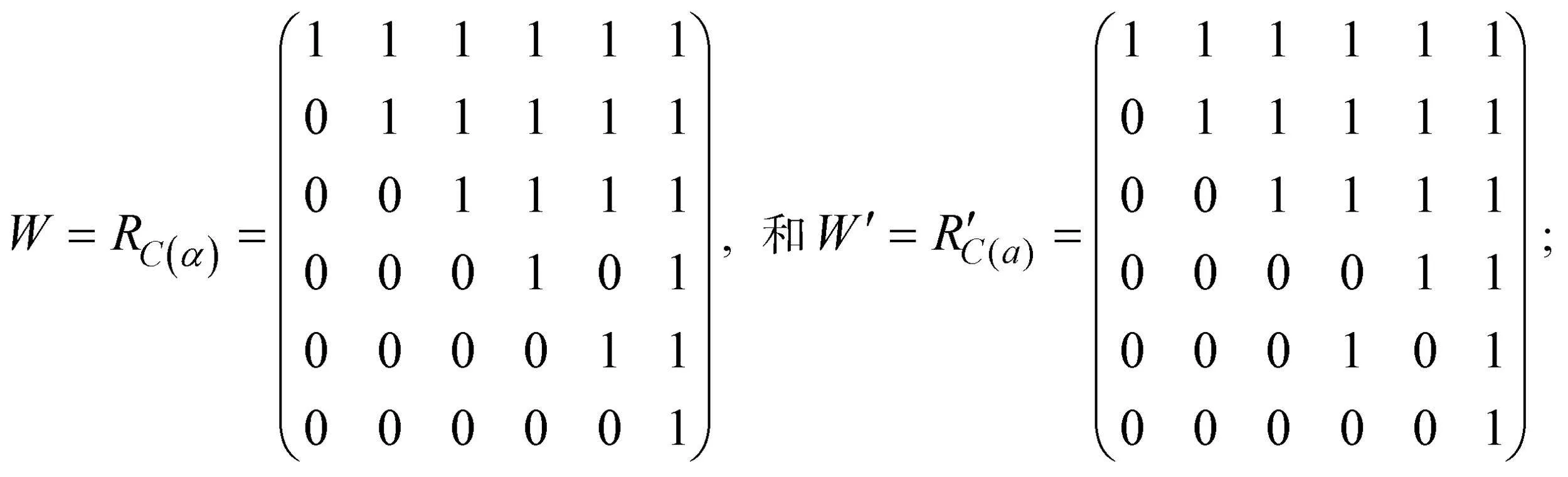
摘 要 Q矩陣的完備性是認知診斷模型具有可識別性的關鍵。多級評分含有比0-1評分更豐富的診斷信息， 卻鮮見多級評分完備Q矩陣的設計研究。用最少的題量獲得最高判準率是測驗設計者追求的目標， 借鑒0-1評分完備Q矩陣的設計方法， 本文提出從可達陣中獲取多級評分結構化/非結構化最簡完備Q矩陣（SSCQM/USCQM）的方法和算法。模擬實驗得出以下結論：（1）測驗含SSCQM/USCQM越多， 判準率越高; （2）當列數相同時， 含多個SSCQM或多個USCQM測驗的判準率與含可達陣測驗的判準率非常接近; （3）對于一些結構， 縱使多個SSCQM/USCQM的列數少于可達陣列數， 其判準率仍不低于可達陣。總之， 短測驗設計優先選擇SSCQM; 長測驗設計優先選擇USCQM。

關鍵詞 多級評分， 測驗設計， 結構化最簡完備Q矩陣， 非結構化最簡完備Q矩陣， 算法

分類號 B841

1 引言

認知診斷評估提供被試潛在認知能力（也即知識狀態， Knowledge State， KS）的診斷信息， 有利于因材施教， 提升學生的能力（Leighton & Gierl， 2007; Tatsuoka， 2009）。在“雙減”背景下， 如何靈活地通過最少的題量實現對學生認知能力的精準診斷， 是測驗設計者面臨的實際問題。在認知診斷測驗中， 刻畫項目與屬性關系的Q矩陣對被試分類的精度有著非常重要的影響（Chiu， 2013; De Carlo， 2011， 2012; Gro? & George， 2014; Liu et al.， 2012， 2013; Madison & Bradshaw， 2015）。通過Q矩陣， 誘導出被試的差異性作答， 差異性越大越有利于用認知診斷模型精準地識別被試， 故基于Q矩陣的認知診斷模型可識別問題受到廣泛關注（Chiu et al.， 2009; Chiu & K?hn 2015; Fang et al.， 2019; Gu & Xu， 2019， 2021; K?hn & Chiu， 2017; Lin & Xu， 2023; Ouyang & Xu， 2022）。

Q矩陣完備性是Q矩陣可識別問題的主要研究內容之一。能夠識別所有被試的Q矩陣稱為完備Q矩陣（Complete Q Matrix）; 否則， 稱為非完備Q矩陣（Uncomplete Q Matrix） （Chiu et al.， 2009; Chiu & K?hn 2015; K?hn & Chiu， 2017）。已有研究表明， 非完備Q矩陣會將一些被試劃分到錯誤的類別中去（Chiu et al.， 2009）， 因此Q矩陣的完備性是可識別的充分或（和）必要條件之一， 是認知診斷模型具有可識別性的關鍵條件（Gu & Xu， 2019， 2021a; Lin & Xu， 2023; Ouyang & Xu， 2022）。根據完備Q矩陣中項目表達是否與屬性層級結構一致， 完備Q矩陣可細分為結構化完備Q矩陣（Structured complete Q Matrix）和非結構化完備Q矩陣（Unstructured complete Q Matrix ） （丁樹良 等， 2022; K?hn & Chiu， 2021）。在現有研究中， 結構化完備Q矩陣以測驗包含可達陣為主， 非結構化完備Q矩陣（除獨立結構外）主要有兩種， 一種為測驗包含單位陣（Chiu et al.， 2009; Fang et al.， 2019; Lin & Xu， 2023; Ouyang & Xu， 2022; Xu & Zhang， 2016; Gu & Xu， 2021b）， 另一種為K?hn和Chiu （2021）提出的新方法， 他們認為， 對于0-1評分， Q矩陣中所有項目遵循某種屬性層級結構不是提高認知診斷分類精度的必要條件， 故提出并證明滿足的非結構化矩陣是非結構化完備Q矩陣（R與E分別表示給定的屬性及其層級關系對應的可達陣和單位陣）。

KS、理想反應模式（Ideal Response Pattern， IRP）和觀察反應模式（Observe Response Pattern， ORP）等三者的關系是認知診斷的核心（丁樹良 等， 2012）， IRP不僅是KS和ORP聯系的紐帶， 更是KS和ORP存在聯系的核心基礎。在沒有項目性質、動機或一些隨機因素等影響下， 完備Q矩陣均能建構IRP與KS的一一對應關系， 如果在這種情況下KS不能被識別， 那么受到上述因素影響的ORP更難識別KS。前述研究較多地考慮了干擾因素， 而忽視了作為核心基礎的IRP和KS間的一一對應關系。故本文關于完備Q矩陣的討論， 著重考察該矩陣是否能夠建立IRP與KS一一對應關系。

較0～1評分， 多級評分可更細致、更深入地探測被試具體的解題步驟或加工過程， 因此能夠提供更多的診斷信息（Ma & de la Torre， 2016）。在多級評分測驗中， 雖然可達陣能大幅提高分類精度（丁樹良 等， 2010; 丁樹良 等， 2011）， 但可達陣不是項目最少的完備Q矩陣， 比如丁樹良、汪文義等人（2014）提出K個屬性的線型結構， 僅需全1列便可使得IRP與KS一一對應， 也即全1列為含項目最少的完備Q矩陣。本文將含項目最少的結構化和非結構化完備Q矩陣分別稱為結構化最簡完備Q矩陣（Structured Simplest Complete Q Matrix， SSCQM）和非結構化最簡完備Q矩陣（Unstructured Simplest Complete Q Matrix， USCQM）。最簡完備Q矩陣（Simplest Complete Q Matrix， SCQM）可用于短測驗（如課堂測驗）， 且以SCQM作為子矩陣的長測驗必為完備Q矩陣， 故多級評分SCQM在Q矩陣設計中有廣泛的應用前景。

多級評分SCQM的設計往往比0-1評分完備Q矩陣的設計難度更大， 囿于我們的視野， 我們僅發現丁樹良、羅芬等人（2014）和丁樹良、汪文義等人（2014）的多級評分完備Q矩陣設計及其理論證明。針對不同的屬性層級結構， 他們分別給出幾種基本屬性層級結構（線型、收斂型、分支型、無結構和獨立結構）的多級評分完備Q矩陣設計方法和證明， 為提高多級評分認知診斷測驗精度和測驗效率提供新的思路和方法。但這兩個研究存在以下問題：（1）針對不同屬性層級結構設計完備Q矩陣的方法不具兼容性， 無法整合， 且在實際應用中， 屬性層級結構更為復雜， 通常由這些基本屬性層級結構復合而成， 如何得到這些復雜結構的完備Q矩陣， 還缺乏相關研究; （2）運用效果未得到模擬驗證。比如線型結構的全1列， 由于該完備Q矩陣測驗較短， 其測量誤差較大， 考慮到重復測量可減少測量誤差， 那么最少要多少個全1列才能和K階可達陣的測量精度相當？這是一個必須回答的問題; （3）未涉及多級評分非結構化完備Q矩陣研究。K?hn和Chiu （2021）試圖將結構化完備Q陣研究拓展到非結構化Q矩陣中， 并發現非結構化完備Q矩陣選擇范圍較廣， 但研究止步于0-1評分， 未能涉及多級評分情況。已有文獻（Fang et al.， 2019; Lin & Xu， 2023; Ouyang & Xu， 2022）提出多級評分的完備Q矩陣包含單位陣， 只含單位陣的測驗設計過于單一， 是否存在其他的非結構化完備Q矩陣使得測驗具有多樣性？這些問題均需進一步討論。

本文在前人研究的基礎上， 擬基于IRP解決如下兩個問題：第一， 提出多級評分SSCQM和USCQM通用的設計方法和算法; 第二， 考察屬性層級結構、屬性個數和項目參數等因素對多級評分SSCQM和USCQM分類精度的影響。以下研究的Q矩陣均為題目水平， 即一個題目對應一個向量。

2 多級評分SSCQM的設計及其算法

考慮到丁樹良、羅芬等人（2014）和丁樹良、汪文義等人（2014）設計和證明的復雜性， 且未能給出統一的、適用于各種屬性層級結構的設計方法， 本研究另辟蹊徑， 首先以完備Q矩陣可建立IRP與KS一一對應關系為導向， 構造SSCQM并加以驗證; 然后提出操作性強、便于使用和推廣、適用于各種屬性層級結構的SSCQM算法。

2.1 多級評分SSCQM的設計

對于0-1評分， 采用DINA理想評分規則（該規則要求屬性之間不可補償）， 將可達陣作為測驗子矩陣可建立被試IRP與KS的一一對應關系（丁樹良 等， 2010; 丁樹良 等， 2011; 丁樹良 等， 2012; K?hn & Chiu， 2021）， 即可達陣為完備Q矩陣。

對于多級評分， 采用被試掌握項目中一個屬性， 理想評分便多一分的評分規則（Tatsuoka， 1995）：

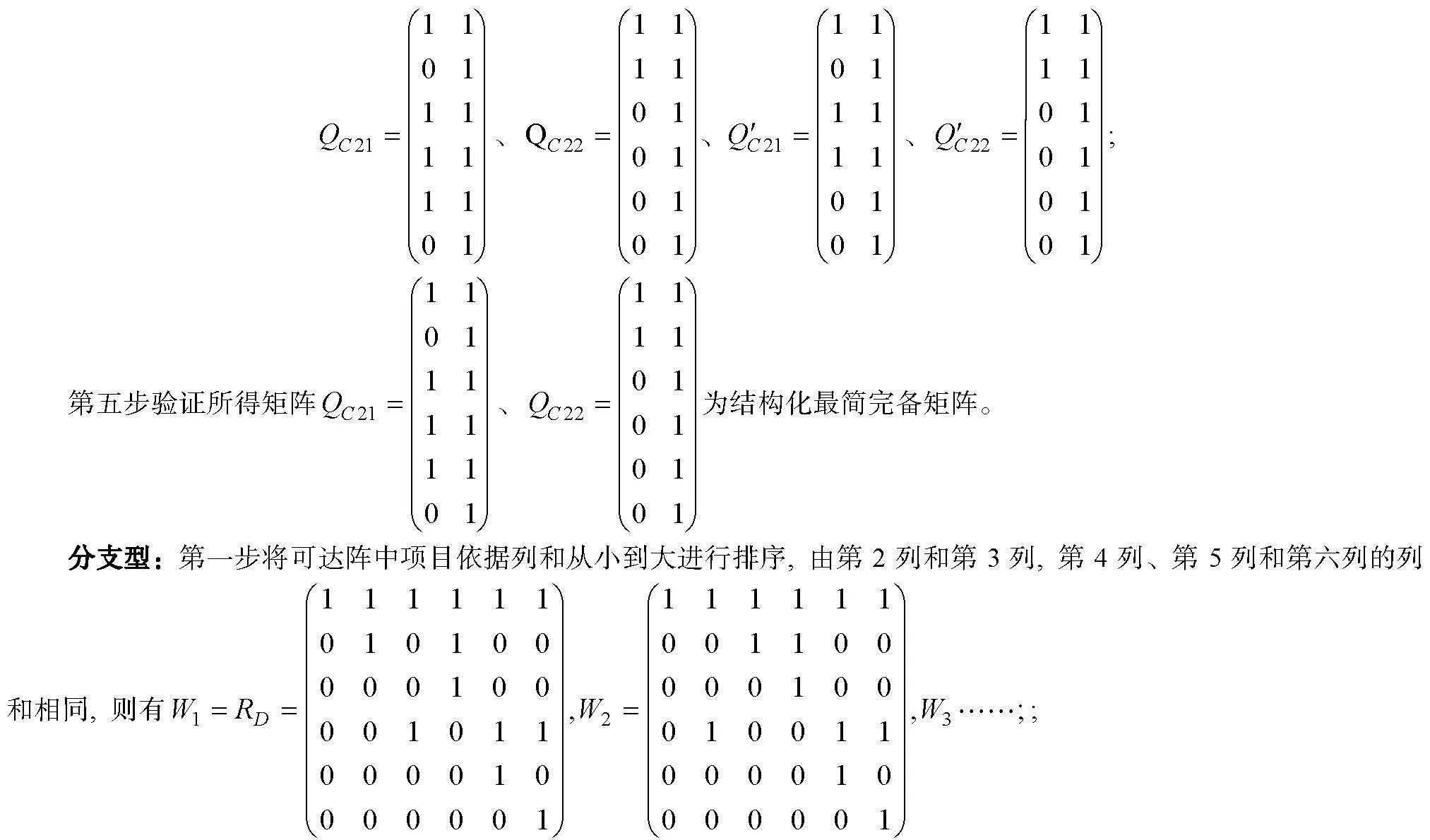
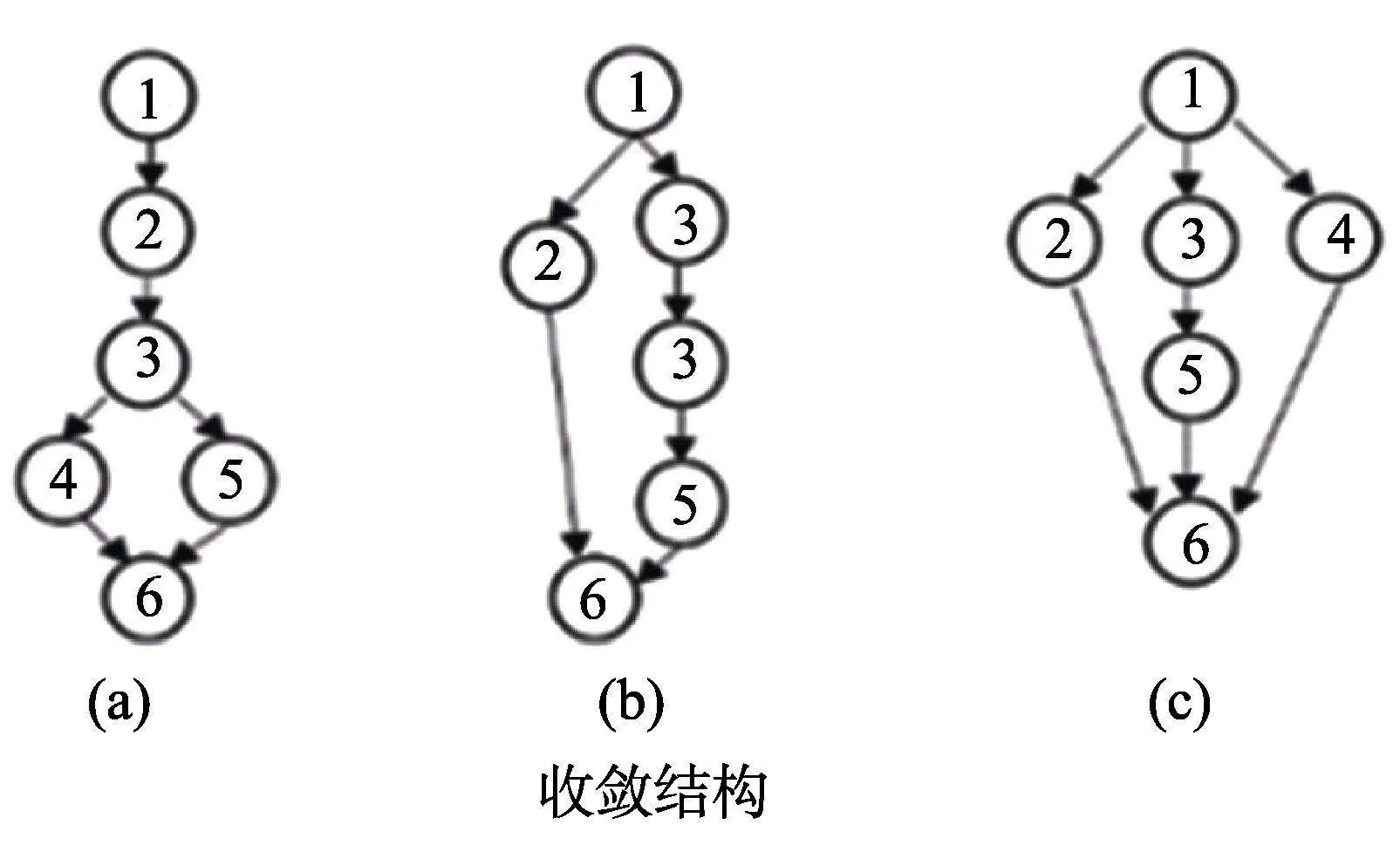
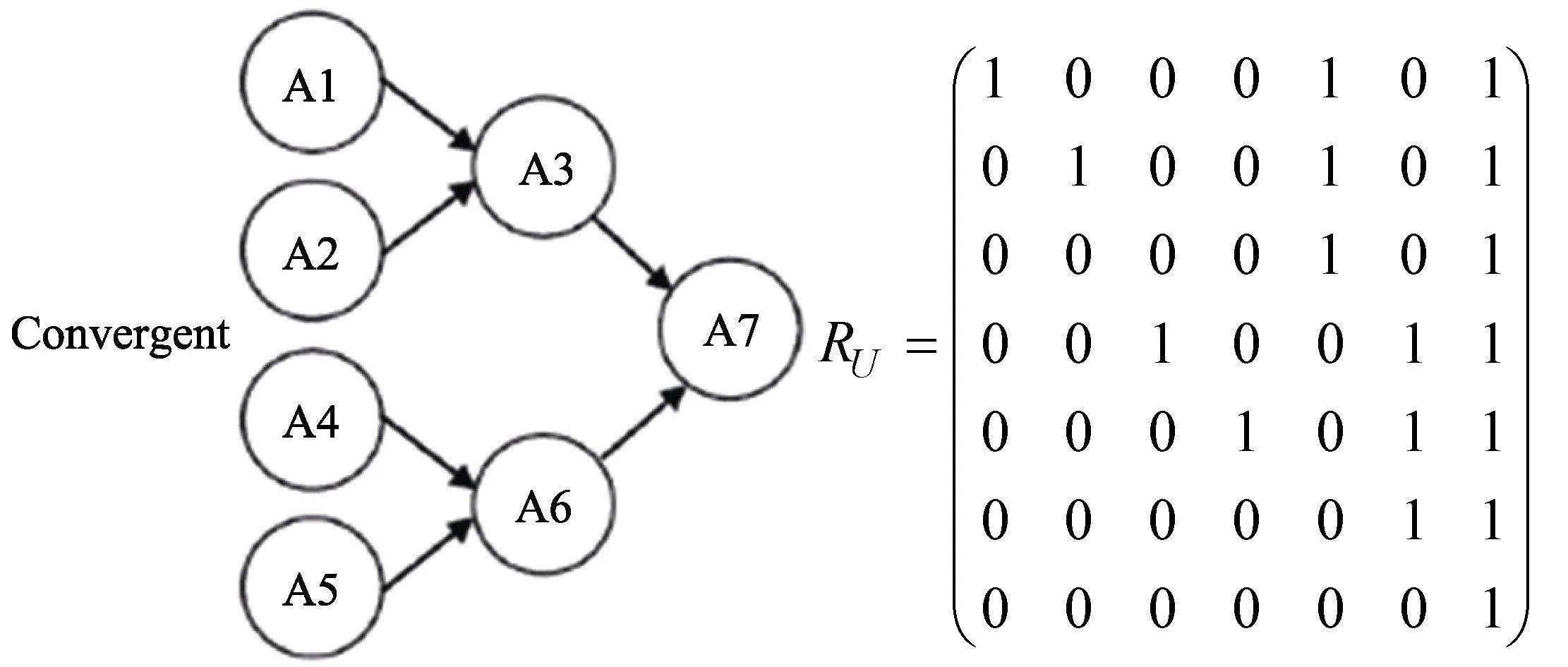
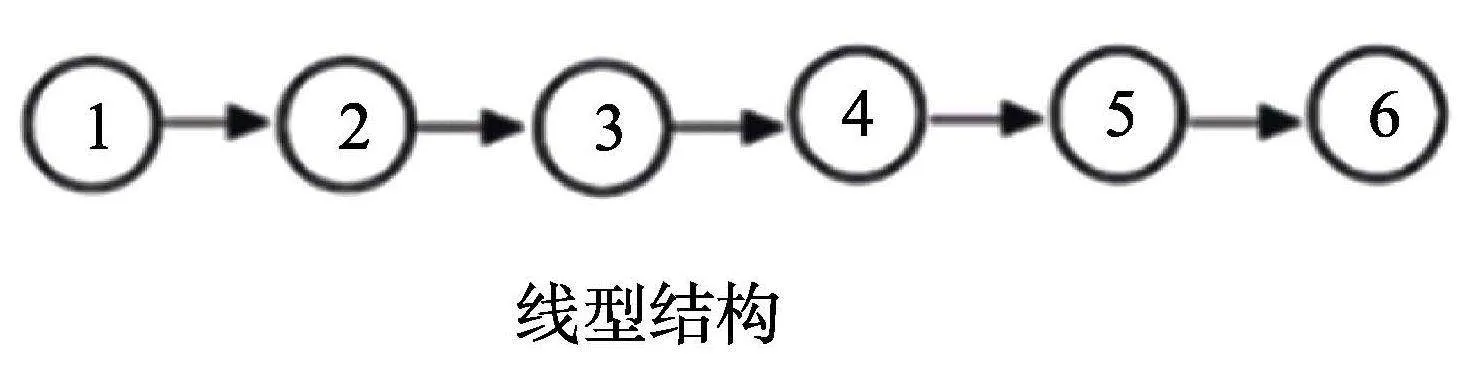
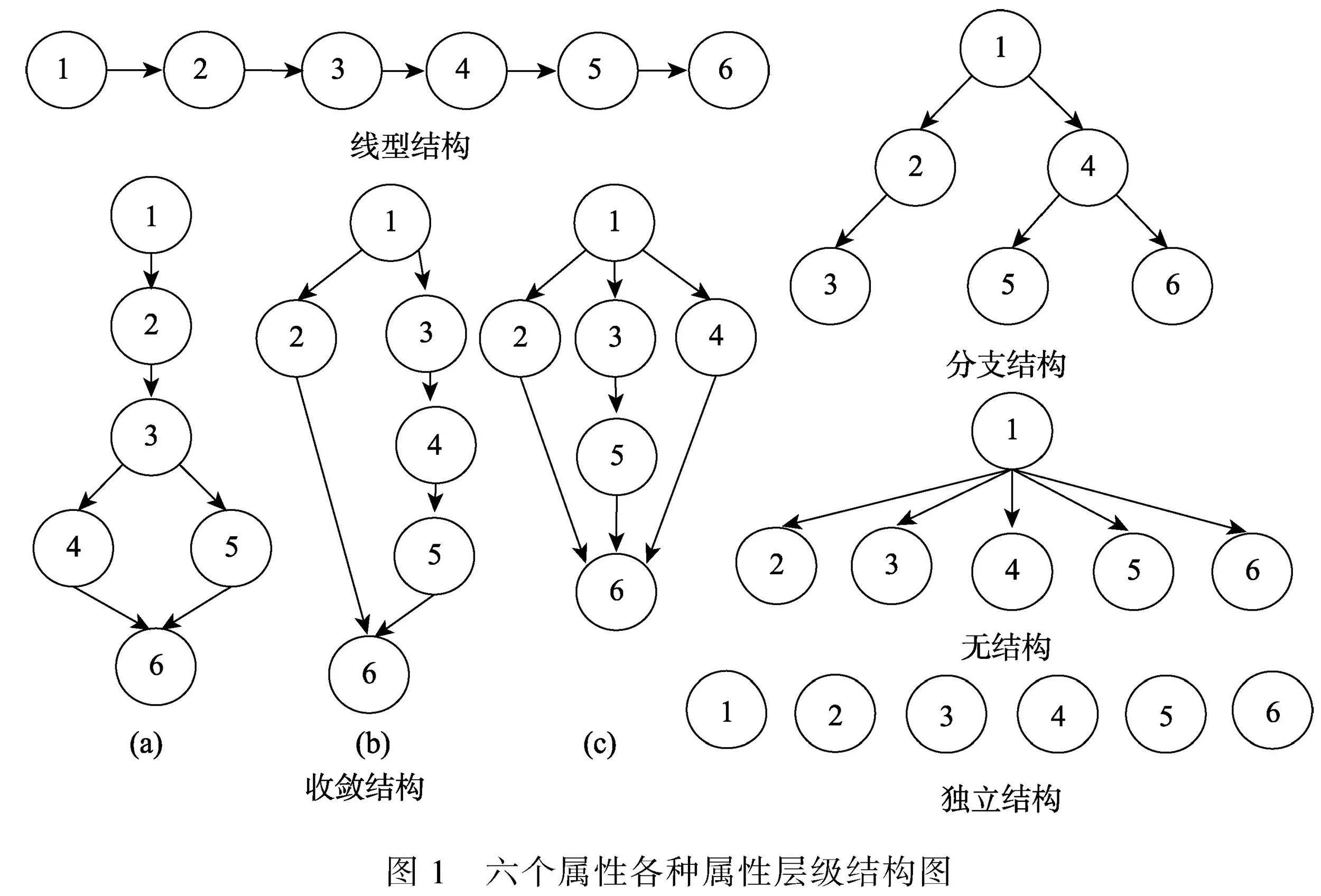
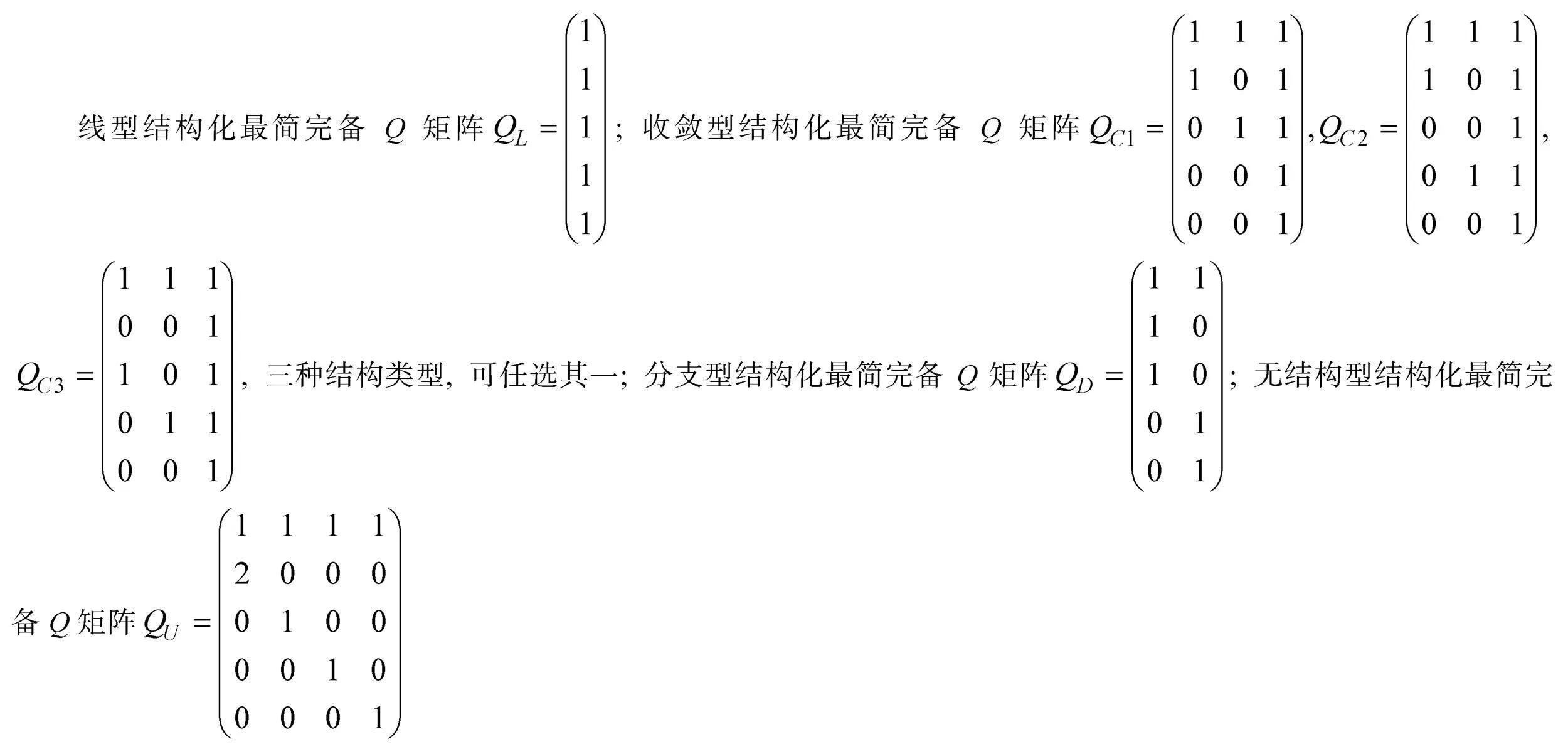
可達陣仍為完備Q矩陣（丁樹良， 汪文義 等， 2014; Sun et al.， 2013）。然而， 除獨立結構外， 其他屬性層級結構的可達陣不是最簡完備Q矩陣， 因此， 以可達陣為研究對象， 對比所有KS在可達陣上的理想反應模式， 刪減可達陣中所有不必要的列， 得到可達陣的子矩陣為最簡完備Q矩陣。下面以6個屬性線型結構為例（見圖1）， 基于公式（1）和（2）， 構造SSCQM并加以驗證。限于篇幅， 直接給出其他4種屬性層級結構（收斂型、分支型、無結構和獨立結構）的SSCQM。

ehlgX8lsXZR50IeHKwK4X/yLMHnp1IOc6ozzouXy+ZA=（1）線型結構

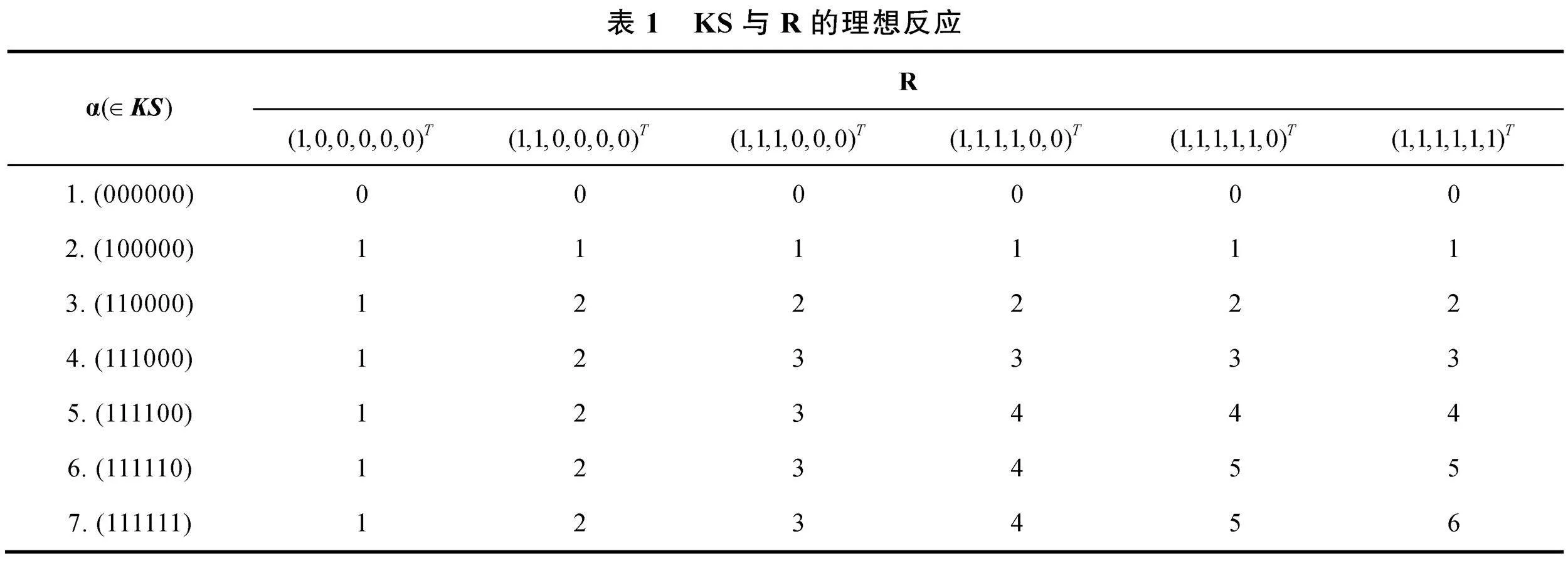
KS類型有7個， 可達陣R為6列， 基于R的理想反應模式如表1。

從表1中最后一列可知， 可達陣中的使得 IRP與KS一一對應， 即為SSCQM。

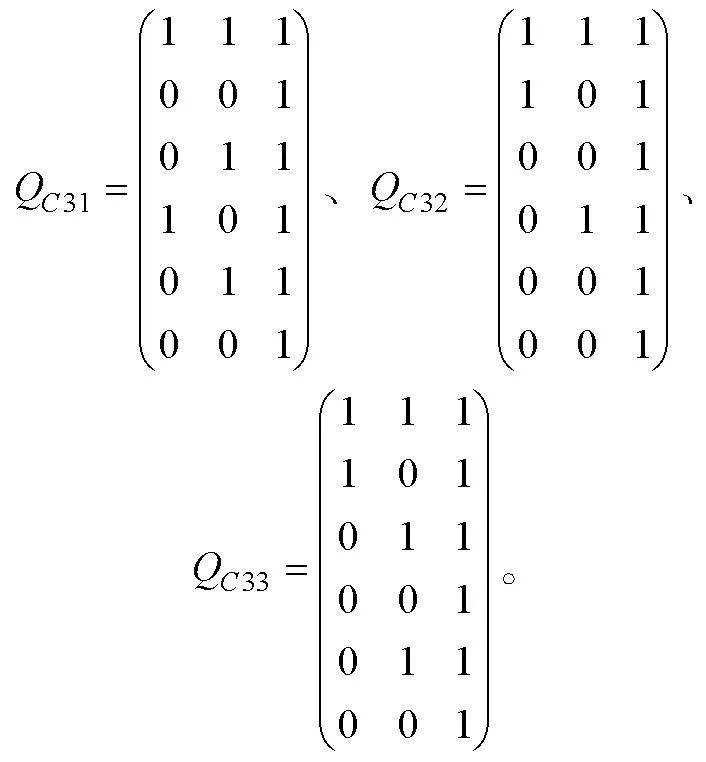
（2）收斂結構

收斂結構（a）的SSCQM為

收斂結構（b）的SSCQM為

收斂結構（c）的SSCQM為

雖然收斂結構有多個SSCQM， 但每一個矩陣所選取的列為收斂結構某一個或幾個不同的分支， 從結構上來說， 這些分支是并列關系。在測驗設計時， 這幾種SSCQM可以任選， 或者如果測驗需要多個SSCQM， 為了盡可能地降低曝光率， 這些矩陣可以混合使用。

（3）分支結構

（4）無結構

（5）獨立結構

SSCQM為可達矩陣。

由5種屬性層級結構的SSCQM可知， 屬性層級結構圖中有幾個分支， 則SSCQM中就有幾列， 且每列的向量對應一個分支。線型結構和收斂型結構的SSCQM含有可達陣的最大列（即全1列）， 而其他3種結構的SSCQM的各個列之間不可比較。

2.2 多級評分SSCQM的算法

定義 設兩個K維向量x和y， 稱當且僅當， 其中 為偏序關系; 若x和y不滿足上述關系， 稱x和y不可比較。

基于可達陣各列之間是否可比較及可比較的大小關系給出算法。將比較所得最大列稱為支柱列。

多級評分SSCQM算法如下：

第一步 輸入可達陣R， 計算可達陣R每列考察屬性的個數和（稱之為列和）， 按照列和從小到大對列進行排序， 如果列和一樣， 則由這些列的全排列所得多個矩陣均需考察， 設W=， 同時生成兩個空矩陣Q1， Q2;

第二步 按列循環求W中的支柱列

for i=1 to [col（W）?1]

{首先， 從W最后1列開始， 若該列大于其他所有列， 設其為支柱列， 則將該列放入Q1中， 若在剩余的列中還存在此類型的列， 則繼續放入Q1中（在此過程中， W的列數不能少于等于2， 否則直接比較列的大小）;

接著， 若， 則從W中刪除與后面的列繼續比較， 刪除小的， 直到找到最大列， 設其為支柱列， 放入Q2中;

若與不可比， 則跳過該列與下一列比較， 若與后面列都不可比， 則將放入Q2中;

若W只剩1列， 該列直接放入Q2中;

最后， 重新計算W的列數col（W）， 直至W中沒有列};

第三步 求Q1的支柱列， 不是支柱列刪除;

第四步 計算屬性層級結構圖中的分支數（設為n）， 若Q1有m列， 則隨機取Q2中的n–m列與Q1合并為一個Q矩陣; 若Q1中沒有列， 則隨機取Q2中的n列構成矩陣Q;

第五步 驗證所得Q矩陣的完備性， 若Q矩陣為完備矩陣， 則輸出Q， 否則， 舍棄。

以收斂結構（c）為例闡述算法的使用步驟（其他結構的算法步驟見網絡版附錄）。第一步， 先將R的列進行排序， 即

因為第2， 3， 4列都考察了2個屬性， 則將這3列全排列， 共6種情況， 對應6個矩陣， 下面就要從這6個矩陣分別提取結構化完備Q矩陣。首先從開始， 生成兩個空矩陣Q1， Q2; 第二步， 首先W中最大列為第6列， 則將該列放入Q1中， 從W中刪除第6列， 此時在W剩下的列中沒有最大列; 接著求W剩下列的支柱列， 第1列比第2列小， 則第1列刪除， 將第2列繼續與后面的列進行比較， 由于不可比較， 則第2列為支柱列， 放入Q2中， 從W中刪除第2列， 這時W只剩3列， 最后重置W的列數， 原來的第3，4，5列重置為第1，2，3列; 首先W的剩余列中沒有最大列， 再求支柱列， 此時W中的第1列與第2列不可比較， 跳過第2列， 由于第1列比第3列小， 將第3列放入Q2中， 刪除W中的第1，3列， 最后W只剩第2列， 也放入Q2中， 故最終Q2有3列， 分別為原W中的第2，4，5列; 第三步， Q1只有1列， 則該列即為支柱列; 第四步， 因為是收斂結構， 由屬性層級結構圖可知該結構有3個分支， 故隨機取Q2中的2列與Q1中的1列分別合并為3個矩陣， 則這三個矩陣分別為 和; 第五步， 經驗證和均為SSCQM。其他5種情況的矩陣所得SSCQM與相同。此算法所得多級評分SSCQM與已有研究結果（丁樹良， 羅芬 等， 2014; 丁樹良， 汪文義 等， 2014）一致。

值得一提的是：（1）第一步的全排列問題。必須將那些列和相等的列進行全排列， 否則只能得到部分SSCQM， 如Sun等（2013）中收斂結構（見網絡版附錄）， 若不全排列， 只能得到2個SSCQM， 但實際上不止2個。（2）有關線型結構的問題。除第1，2列， 線型結構可達陣中其他列全部放入放入Q1中， 第2列放入Q2中， 因為Q1中支柱列為全1列， 屬性層級結構圖中只有1個分支， Q2中項目不計， 故該支柱列即為所求。（3）第四步的計算屬性層級結構分支數問題。一般地， 若屬性層級結構圖分支較清楚（例如5種基本屬性層級結構或者其簡單的組合）， 可直接計算其分支數; 若屬性層級結構圖的分支較復雜， 則可不用計算其分支數， 直接從Q2中分別取1列， 2列， ……與Q1合并為一個Q矩陣， 再驗證所得Q矩陣的完備性。比如K?hn和Chiu （2021）給出11個屬性的屬性層級結構， 分支較復雜， 由算法可得Q1有2列， 即可達陣（已按列和排序）第10， 11列， Q2有2列， 分別為第3 （考察了第3個屬性）， 6列， 先從Q2中取1列與Q1合并成列數為3列的矩陣， 經驗證這兩個矩陣均不是完備Q矩陣， 接著將Q2與Q1合并為一個4列的矩陣， 經驗證該矩陣為SSCQM。

3 多級評分USCQM的設計及其算法

在SSCQM設計的基礎上， 本研究進一步探討USCQM的設計方法和算法。

3.1 多級評分USCQM的設計

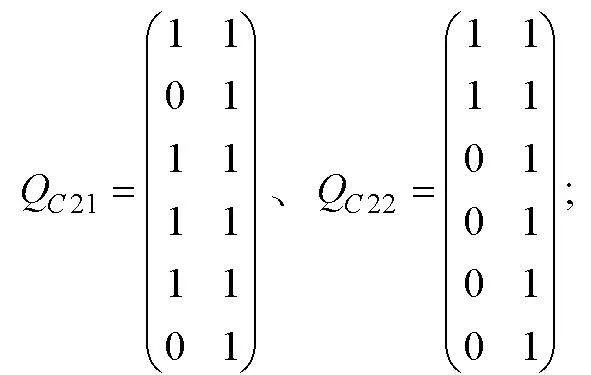
0-1評分非結構化完備Q矩陣介于單位陣和可達陣之間（K?hn & Chiu， 2021）， 其中可達陣為結構化完備Q矩陣， 單位陣為非結構化完備Q矩陣（除獨立結構外）。借鑒0-1評分的思路， 在多級評分中將SSCQM作為上限， 單位陣子矩陣作為下限。設可達陣R（各列依次按照考察屬性的順序排列）， 若上限SSCQM的列對應于R的列號為， 則下限將單位陣E中相同列號的列構成單位陣的子矩陣。以收斂結構（a）為例， 設可達陣R， SSCQM的列對應于R的列號為， 即

取同階單位陣的第5， 6列構成單位陣子矩陣

找出介于和之間所有矩陣， 即 ， 且每行至少有1個“1”（目的是保證每個屬性都要被考察）， 例如

同樣， 對應可達陣的第4，6列， 單位陣子矩陣的第4，6列為

且每行至少有1個“1”， 例如

相較于2個SSCQM， 符合條件的USCQM 和均有53個。

3.2 多級評分USCQM的算法

根據上述設計原理， 多級評分USCQM算法如下：

第一步 輸入結構化最簡完備Q矩陣和其對應的單位陣子矩陣

， 用得到矩陣Q0=（qij）;

第二步 隨機將Q0中一個或多個qij=1替換為qij=0;

第三步 將（2）產生的矩陣與單位陣子矩陣相加得到矩陣;

第四步 驗證矩陣列的布爾并是否為全1列且該矩陣是否完備， 若是， 則輸出矩陣， 否則舍棄。

4 基于多級評分認知診斷模型的SCQM

4.1 多級評分認知診斷模型

大部分多級評分認知診斷模型是從0-1評分認知診斷模型拓展而來。高旭亮等人（2021）詳細地介紹了三種類型的多級評分認知診斷模型：（1）鄰接類別模型（adjacent category models）; （2）連續比率模型（continuation ratio models）; （3）累積概率模型（cumulative probability models）。因完備性的驗證涉及認知診斷模型， 下面只介紹與本研究有關的GPDINA模型（Chen & de la Torre， 2018）和RP-DINA模型（蔡艷 等， 2017）。

GPDINA模型是GDINA模型（the generalized DINA model） （de la Torre， 2011）與GPDM模型（the general polytomous diagnosis model） （Chen & de la Torre， 2018）的融合。

PDINA模型：

也即

因為PDINA構建的理想評分只有0和1， 影響分類的精度， 蔡艷等人（2017）修改了PDINA模型的評分方式， 提出了RP-DINA模型。RPDINA模型：

RPDINA模型中其他符號定義與PDINA模型一致。研究表明由于RPDINA模型中評分的修正， 使得其判準率比PDINA模型的高。

4.2 結合多級評分認知診斷模型的SCQM的驗證

進一步， 基于理想反應模式與知識狀態一一對應關系建構的SCQM， 結合認知診斷模型， 驗證其是否仍具完備性。

（1）給出評分方式。在多級評分中， 完備Q矩陣與評分方式和滿分值有關， 會影響Q矩陣診斷信息的質量（丁樹良， 汪文義 等， 2014）。如若采用蔡艷等人（2017）提出的評分方式和滿分值， 則可達陣不是完備Q矩陣（見討論部分）。因完備Q矩陣可以提高診斷判準率， 故在下面驗證中， 認知診斷模型采用公式（1）的評分方式和公式（2）滿分方式。

（2）驗證Q陣完備性。K?hn和Chiu （2021）提出的完備性驗證方法為當觀察反應模式的期望相等時， 對應的KS相同。

被試在上期望為

結合認知診斷模型， 驗證本文提出的SCQM的完備性， 其中， SSCQM選取2.1中線型的， USCQM選取3.1中收斂型的I1。

對于PDINA模型， 因為理想評分還是按照0-1評分方式， 只有被試掌握項目中所有屬性， 交互才存在， 若在項目中至少一個屬性是被試未掌握的， 則該類被試均不能被識別， 故與不是完備Q矩陣。PDINA的SSCQM為可達陣， USCQM陣有多個， 其中一個為單位陣。

對于RPDINA模型， 結果如表2。

由表2可知， 不同則所對應的也不相同， 故按照本文提供的評分方式， 對于RPDINA模型， 為結構化完備Q矩陣， 因為只有1列， 即是SSCQM。

根據表3的計算結果， 因各個在I1上的不等， 且刪減任一個項目使得至少有兩個的相等， 故是USCQM。同理， 可以證明也是USCQM。

對于PACDM模型， 與仍為完備矩陣， 對于PDINO模型， 與不是完備矩陣。

從例題似乎可以看出， 只要認知診斷模型的主效應存在， SCQM的完備性不變。

5 模擬實驗研究

從IRP的角度， 與可達陣一樣， 1個SCQM能將KS完全區分， 然而， 在實際應用中， 由于1個SCQM列數較少， 則存在測量誤差， 使得其判準率（PMR或者MMR）不一定高于（甚至抵不上）可達陣。為研究多級評分SSCQM和USCQM的分類效果， 模擬實驗主要考察當SCQM的列數不超過可達陣的列數時， 到底需要多少個SSCQM/USCQM才能達到或相當于可達陣的分類精度。為避免概念混淆， 下文中的結構化完備Q矩陣均不包含可達陣。為更好地與實踐中的終結性評估和過程性評估相對應， 本研究擬構造長測驗和短測驗， 并從屬性層級結構（如圖1和網絡版附錄）、項目參數和屬性個數等方面， 分別考察（含）SSCQM、USCQM和可達陣三種矩陣的認知診斷測驗分類效果， 研究均采用python自編程序模擬和分析數據。

5.1 研究1：考察在不同屬性層級結構下項目參數對三種測驗的影響

5.1.1 實驗設計

屬性個數K = 6， 被試數N = 2000。由于獨立結構的SSCQM即為可達陣， 不存在非結構化Q矩陣， 故本研究只涉及線型、收斂型（a）（b）（c）、分支型和無結構等屬性層級結構。研究從如下兩個方面展開：第一， 比較一個和多個SSCQM/USCQM（總列數不超過可達陣的列數）與可達陣分類能力的高低; 第二， 在多個SSCQM/USCQM的基礎上， 相應地添加SSCQM/USCQM中的列（添加的列數小于SCQM的列數）， 使得總列數與可達陣列數一樣， 比較它們的診斷分類效果。

5.1.2 Monte Carlo模擬

（1）被試屬性掌握模式真值模擬

被試平均分配給各個屬性層級結構的KS， 不能均分的， 則隨機指派。

（2）測驗Q矩陣及其項目參數模擬

長測驗題目總數為40題。測驗分別包含1個可達陣、1個或多個不同屬性層級結構的SSCQM和USCQM（總列數不超過可達陣列數）， 剩下的題目從結構化/非結構化的非完備Q矩陣中選取。

短測驗題目總數為6題（即可達陣的列數）， 測驗分別為1個可達陣、含最多個數的SSCQM和USCQM（剩下的題目從SSCQM/USCQM中選取， 使得總列數等于可達陣的列數）。

（3）被試作答反應的模擬

由被試真值和測驗Q矩陣， 按照公式（1）和（2）得到理想得分矩陣， 然后根據RPDINA模型模擬被試得分。

（4）被試KS估計方法

采用RP-DINA模型和最大后驗估計方法（Maximum A Posteriori， MAP）估計被試的KS。

（5）評價指標

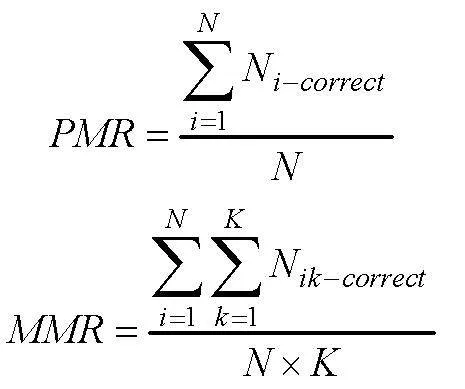
采用模式判準率（Pattern Match Ratio， PMR）和屬性邊際判準率（Marginal Match Ratio，MMR）作為分類能力的評價指標。

其中， N為被試總數， 表示被試i的屬性掌握模式是否判對， 判對為1， 否則為0; K為屬性個數， 表示被試i的屬性k是否判對， 判對為1， 否則為0。

模擬實驗重復100次（由于可供選擇的USCQM較多， 故從中隨機選取）， 取PMR和MMR的平均值。

5.1.3 研究結果

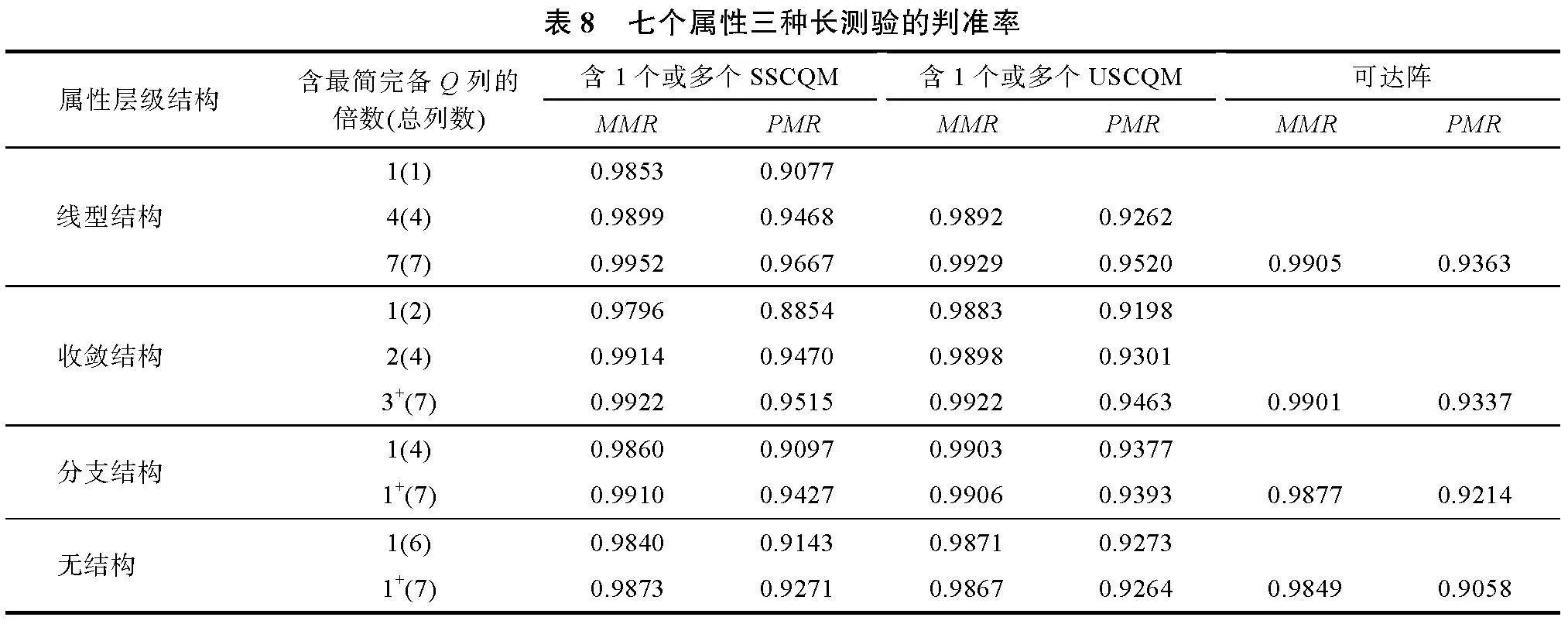
（1）長測驗研究結果

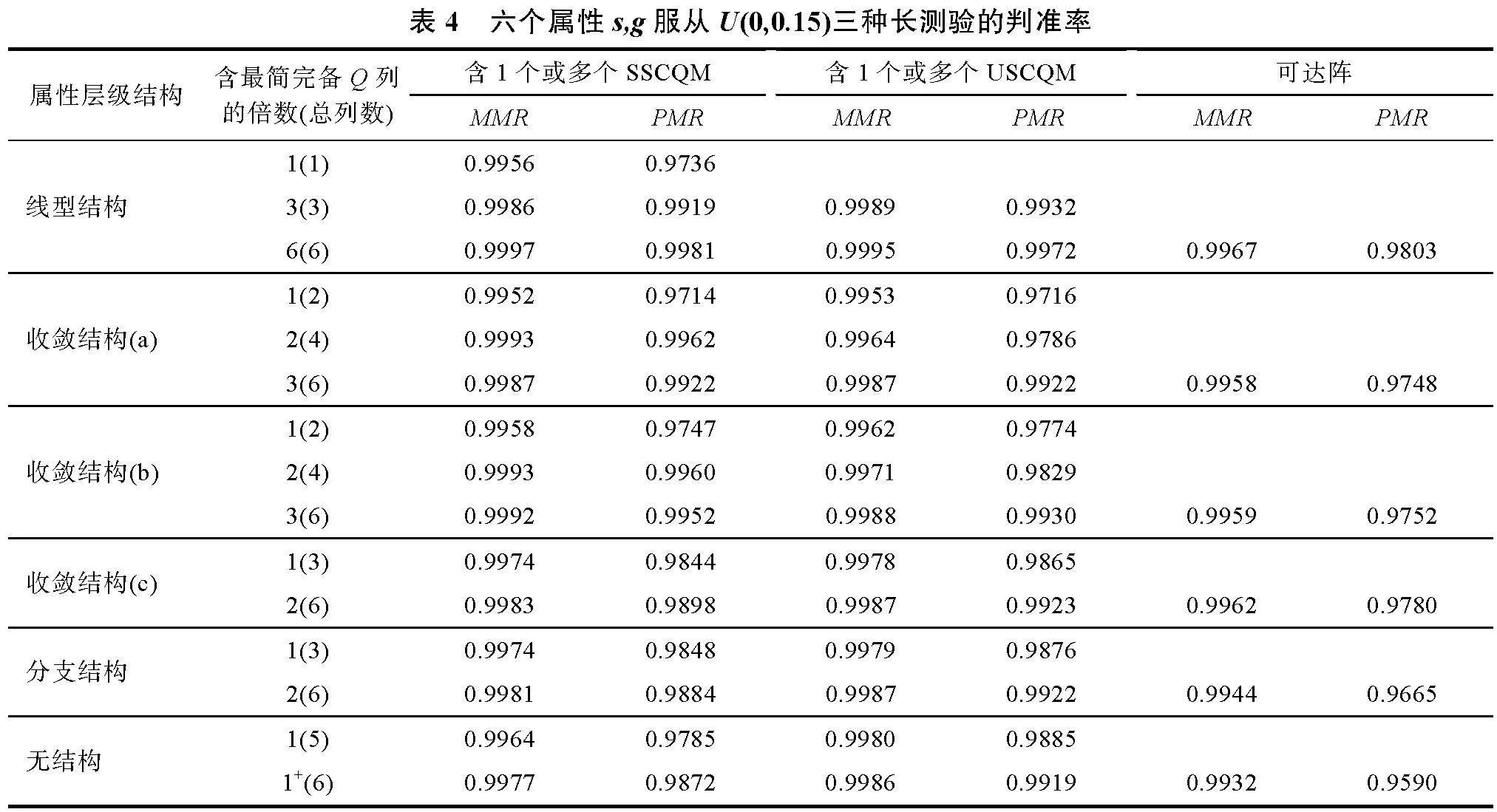
基于三種不同的項目參數設置， 表4～表6按照線型結構、收斂結構、分支結構和無結構等屬性層級結構順序給出了包含1個或多個SSCQM、USCQM和可達陣等三種測驗的PMR和MMR均值。

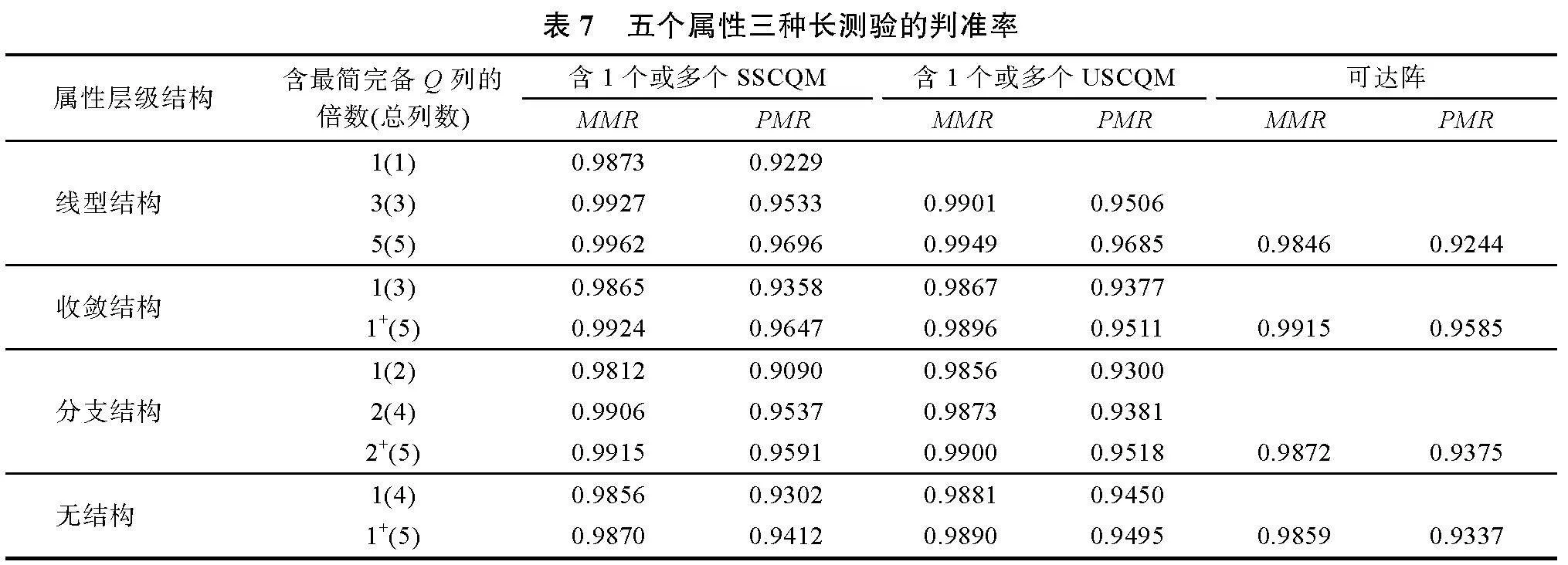
表4給出了屬性個數為6、被試數為2000、s， g服從U（0，0.15）的長測驗的模擬結果： （a）按照屬性層級結構順序， 三種測驗的判準率依次降低， 其中PMR降幅低于3%， MMR降幅不超過0.5%。（b）對于各個屬性層級結構， 含SSCQM/USCQM越多， 則判準率越高， MMR均在0.99以上， PMR均在0.95以上。（c）當多個SSCQM/USCQM的列數少于可達陣的列數時， 比如線型結構3列、收斂結構（a）（b）4列、收斂結構（c） 3列、分支結構3列和無結構5列， 其測驗的判準率均大于含可達陣（6列）測驗的判準率。（d）當列數等于可達陣列數時， 按照屬性層級結構順序， 含SSCQM測驗的判準率逐漸小于含USCQM測驗的判準率， 含可達陣的測驗判準率最低， 但三種測驗的判準率相差不大， PMR的差值不超過0.05， MMR相差更小。表5、表6表明， 在不同的項目參數s， g水平條件下， 結論類似。

表4～表6也表明， 對于同種屬性層級結構， 隨著s， g參數水平的提升， 各種測驗的PMR均降低2%～6%， MMR降低0.3%～1%; 對于相同參數， 按照屬性層級結構的順序， 三種測驗的判準率降幅依次增大， PMR均降低1%～5%， MMR降低0.2%～1%。綜合表4～表6的結果可見：屬性層級結構與項目參數對多級評分SSCQM和USCQM判準率的影響類同。

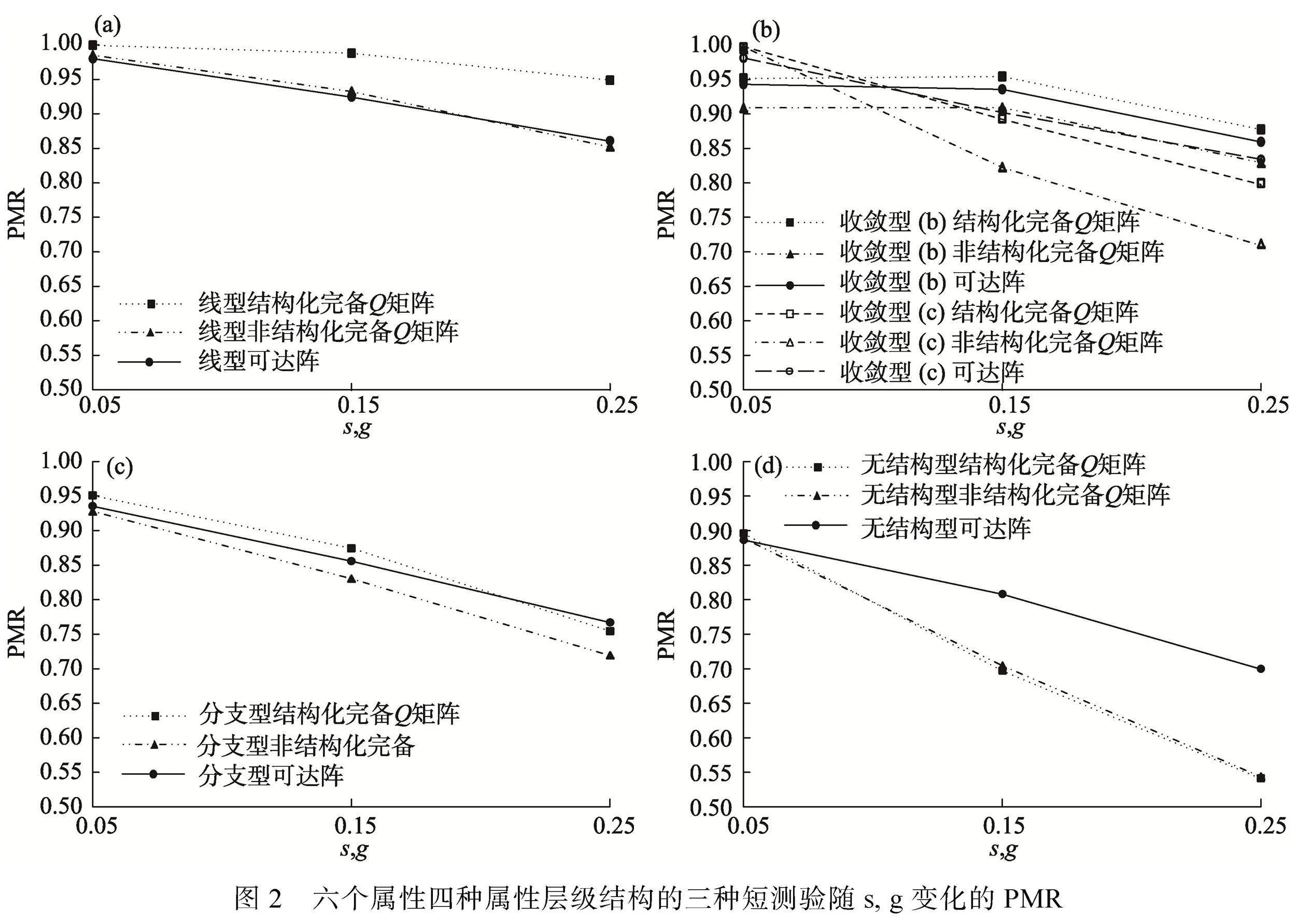
（2）短測驗研究結果

基于三種不同的項目參數設置， 按照線型結構、收斂結構、分支結構和無結構等屬性層級結構順序， 圖2分別給出了多個SSCQM、多個USCQM（其總列數均等于可達陣列數）和可達陣等三種測驗的PMR均值。因為收斂結構（a）判準率的變化與收斂結構（b）的一致， 故圖2只呈現收斂結構（b）（c）的結果。

由圖2可知：（a）隨著屬性層級結構的變化和參數的增加， 三種測驗的判準率均下降， 且差值逐漸增大， 特別是當屬性層級結構為無結構且參數值為0.25時， 可達陣的判準率與其他測驗的判準率相差最大; （b）除無結構外， 當s和g相同且屬性層級結構相同時， 三種測驗的判準率相差不超過0.1; （c）在大多數情況下， 多個SSCQM的判準率比可達陣的判準率高， 但當參數較大時， 收斂結構（c）和無結構的情況相反; （d）多個USCQM的判準率幾乎是最低的。事實上， 多個SSCQM和可達陣均是結構化完備Q矩陣， 多個USCQM是非結構化完備Q矩陣， 總而言之， 對于短測驗， 當列數相同時， 結構化完備Q矩陣的判準率高于非結構化完備Q矩陣的判準率。

5.2 研究2： 考察在不同屬性層級結構下屬性個數對三種測驗的影響

一般地， 隨著屬性個數的增加， 測驗的判準率會降低。屬性個數對SCQM的影響程度是研究2繼續探索的問題。

5.2.1 Monte Carlo模擬

（1）在研究1模擬條件的基礎上， 考察5～8個屬性的4種屬性層級結構（如網絡版附錄， 6個情況如研究1）。

（2）項目選取如研究1， 固定測驗參數， 長測驗

參數和服從， 短測驗參數和

服從。

（3）被試真值、評分和評價指標均如研究1。

5.2.2 研究結果

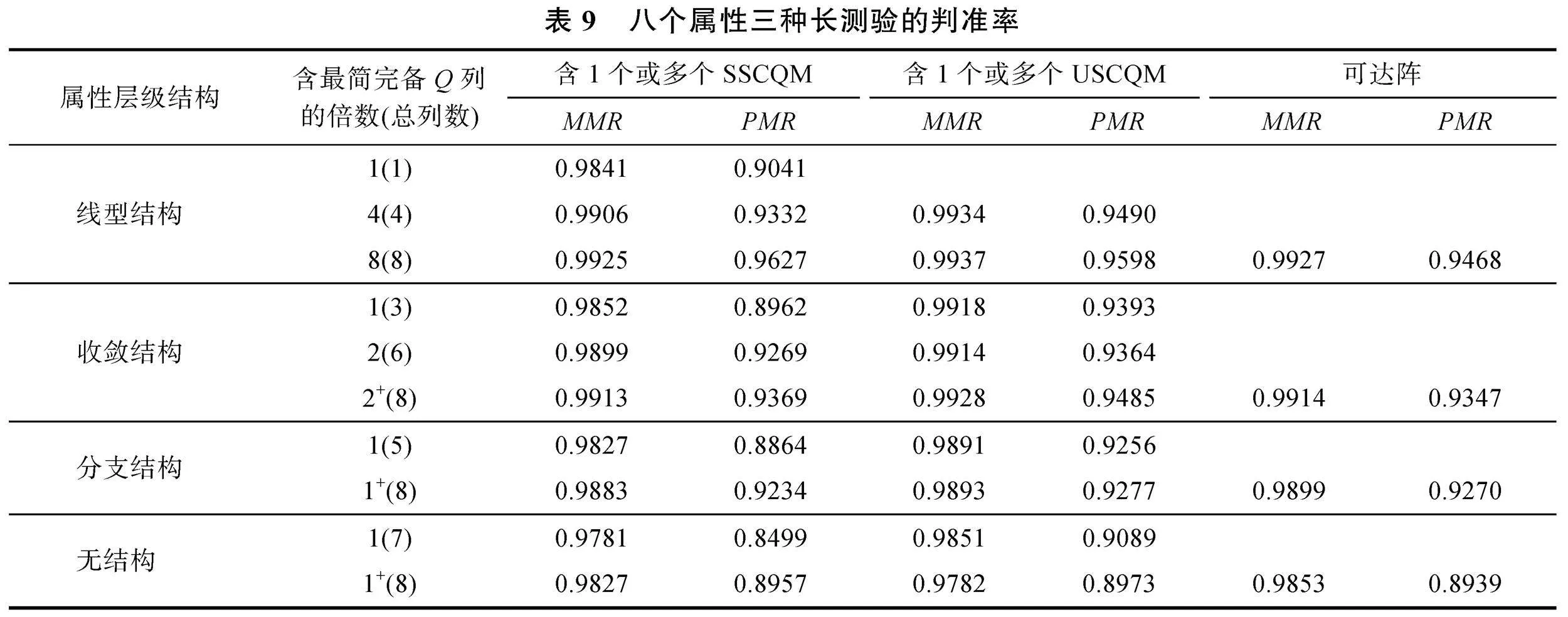
（1）長測驗研究結果

表7～表9給出了被試數為2000， 服從U（0， 0.35）， 5～8個屬性的模擬結果：（a）總體上， 隨著屬性個數的增加和屬性層級結構的變化， 三種測驗

的判準率皆呈下降趨勢， 但PMR仍在0.88以上， MMR在0.97以上。（b）當屬性個數一定時， 按照屬性層級結構的順序， 三種測驗PMR降幅為2%～8%， MMR降幅為0.5%～2%; 當屬性層級結構一定時， 按照屬性個數增加的順序， 三種測驗PMR降幅為0.1%～5%， MMR降幅為0.1%～1%。（c）當列數相同時， 三種測驗的判準率相當， 差值很小（PMR差值介于0.001～0.05之間， MMR差值更小）， 其中含可達陣的測驗最差; 當屬性個數為5～7時， 含SSCQM的測驗較優; 當屬性個數為8時， 含USCQM的測驗較優。（d）對于一些含多個SSCQM的測驗， 當列數達到一定數量時， 即便少于可達陣的列數， 其判準率依然高于可達陣， 比如線型結構， 5或6個屬性達到3列， 7個屬性達到4列; 5個屬性分支結構達到4列; 7個屬性收斂結構達到4列， 無結構達到6列等。含多個USCQM的測驗也有類似情況。

由表7～表9的實驗數據可知， 屬性個數的增加對判準率的影響與屬性層級結構所帶來的影響相差不大。

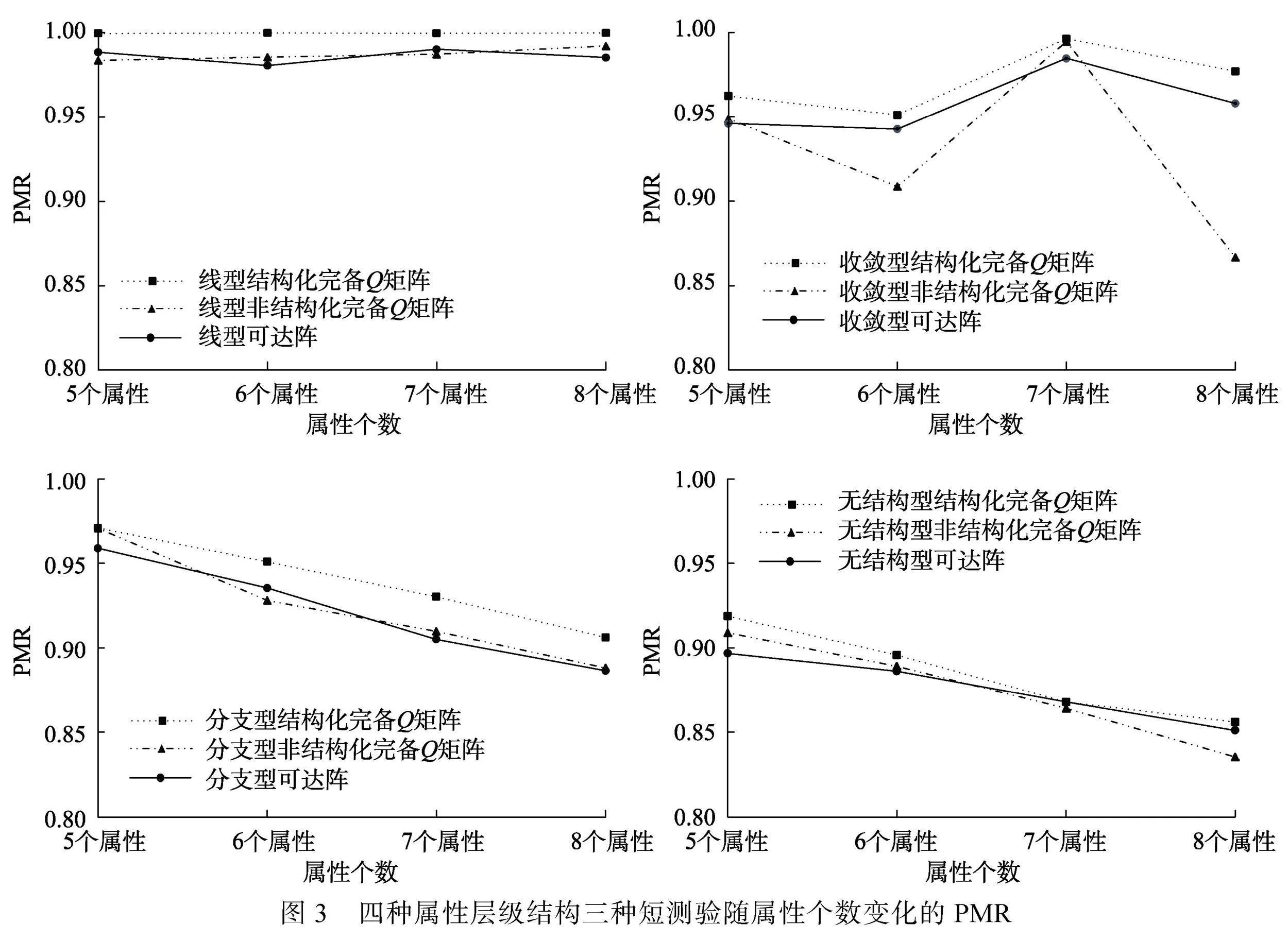
（2）短測驗研究結果

基于不同的屬性個數和不同的屬性層級結構， 圖3分別給出了列數等于可達陣的多個SSCQM、多個USCQM和可達陣等三種測驗的PMR均值。由圖3可知， 題目質量較好時， 隨著屬性個數的增加， 多個SSCQM的判準率最高， 其他兩種矩陣判準率各有高低， 但三者判準率的差值均不超過0.05（除收斂結構8個屬性外）。

根據以上長、短測驗的模擬結果可知：三種測驗的判準率相差不大， 差值為0.05左右; 對于長測驗， 按照屬性層級結構順序（從線型結構到無結構），

當屬性個數為5～7或項目參數較小時， （含）多個SSCQM測驗優于（含）多個USCQM測驗; 當屬性個數為8或隨著項目參數增加， 情況相反; 對于短測驗， 多個SSCQM測驗優于多個USCQM測驗。

6 實證數據分析

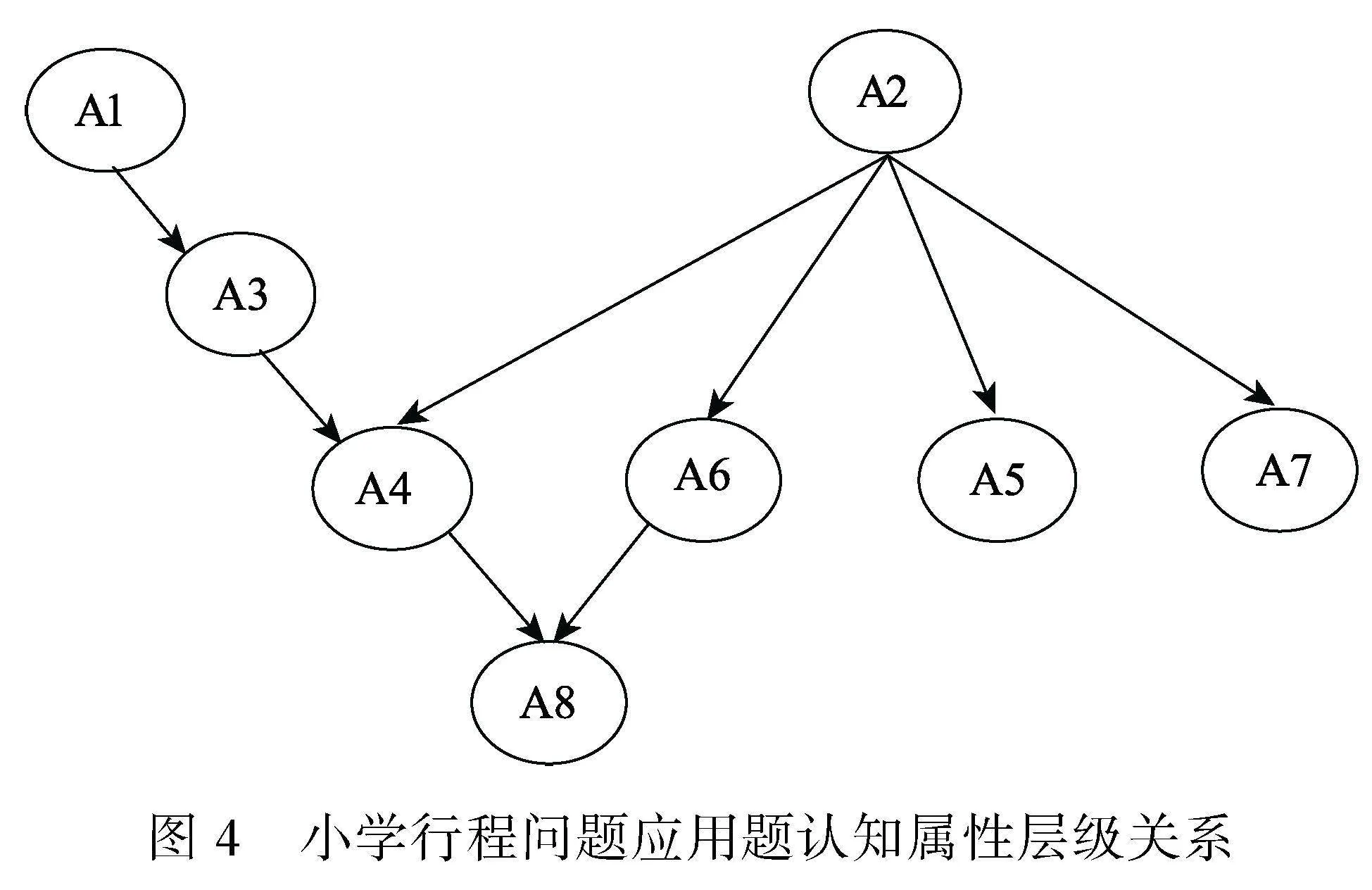
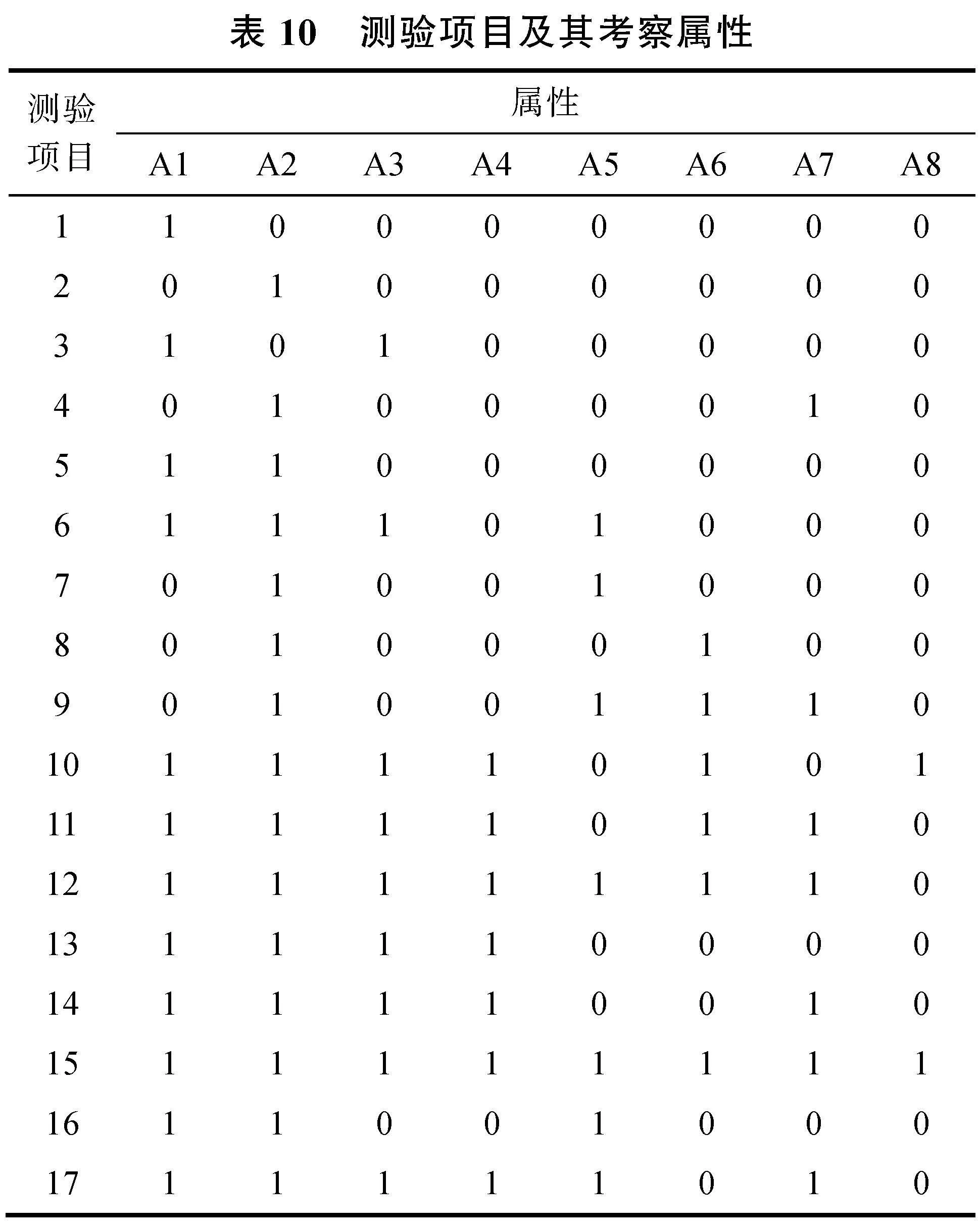
為了進一步驗證SCQM的性能， 下面采用康春花等（2013）的實證數據進行分析。數據收于浙江金華和溫州兩地8所小學， 共1300名被試， 有效被試1240人， 測試內容為五年級小學行程應用題， 共17個題（包含可達陣）， 涉及8個屬性（見表10）， 包括基本算數運算、一般行程問題關系式、等級復雜性、復雜行程問題關系式、識別隱含條件、關系表征、圖式表征和正規代數策略， 屬性層級關系如圖4。該結構由線型、收斂型和無結構復合而成。

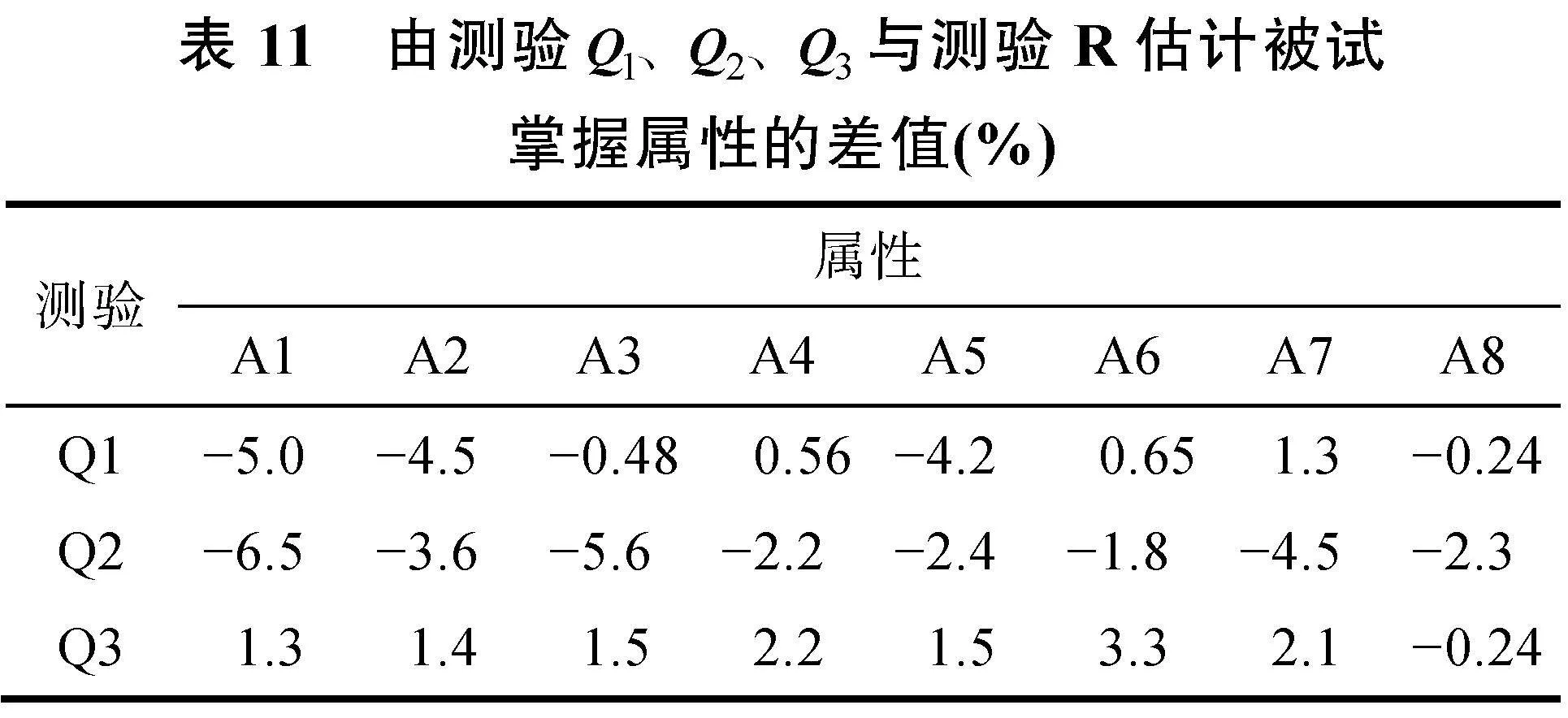
本研究考察4種測驗：包含可達陣的原測驗（設為）和包含1個SSCQM且題量不同的三個測驗（分別設為測驗Q1、Q2、Q3， 均不包含可達陣）， 其題量依次為14題、15題和16題。根據屬性層級結構， 由擴張算法， 得到39種知識狀態。從數據分析結果可知， 測驗Q1、Q2、Q3和測驗可識別的知識狀態類型分別為24種、25種、21種和22種; 測驗Q1、Q2、Q3分別與測驗可識別的相同知識狀態個數分別為1150個、1124個和1175個， 分別占總人數比的93%、90%和95%， 也即含SSCQM估計的被試與含可達陣估計的被試重復率達90%以上， 且用題量均少于可達陣; 測驗Q1、Q2估計的知識狀態類型比測驗R的多， 分類更細。三種測驗估計的被試在各個屬性的掌握比例與測驗R的相差不超過7% （見表11）。

7 討論

7.1 關于多級評分方法與完備Q矩陣的關系

一般地， 對于多級評分來說， 若評分方式和滿分值不一樣則完備Q陣不一樣。本研究是基于評分方式（1）式和滿分值（2）式， 提出了多級評分SCQM的設計方法。對于這種評分方式和滿分值， 可達陣為完備Q矩陣; 若評分方式和滿分值發生改變， 則可達陣可能不是完備Q矩陣， 如蔡艷等人（2017）提出減少滿分值， 評分采用取整的方法， 使得一些本該在（1）式和（2）式條件下不同的作答結果變得相同， 故可達矩陣的完備性發生了改變。以4個屬性線型結構為例， 其中可達陣項目 和， 四個項目的分值分別設為0.5分， 1分， 2分和3分， 根據文中算法， 被試和在可達陣上理想反應模式均為（0000）， 也即無法區分， 若采用（1）式和（2）式， 則可達陣仍為完備Q矩陣。事實上， 若每個屬性的評分權重一樣， 則當每題的滿分值大于等于考察屬性總數時， 可達陣仍為完備Q矩陣， 基于可達陣提煉的SCQM的完備性不發生改變。這一良好的性質拓展了SCQM的適用范圍。若每個屬性評分權重不一樣， 則上述結論不一定成立。

7.2 測驗的投入產出比

測驗是需要時間成本和經濟成本的， 因此， 提高測驗效率， 用最少的題量實現對被試最大限度地區分， 是測驗設計孜孜以求的目標。投入產出比被定義為判準率（MMR和PMR）除以投入的項目數以及估算時間， 數值越大表示單位時間以及每個題目上所得判準率越高， 即投入產出比越高。這個指標充分體現在短測驗中， 在四種屬性層級結構下， SSCQM/USCQM的投入產出比均大于可達陣， 其中， 線型結構的最簡完備Q矩陣題量最少， 因此不論從出題量還是估計被試來說， 其時間花費少， 投入產出比最大。如在短測驗中6個屬性線型結構的SSCQM（只有1列）， 其投入產出比為0.9611/0.3318× 1=2.90， 而可達陣的分別為0.9845/1.0389×6=0.16。收斂結構的SSCQM/USCQM的投入產出比為0.93和1.08， 而可達陣的約為0.17。SSCQM/USCQM是投入產出比較高的測驗。但SSCQM數量非常有限， 在考慮曝光率等因素時， 還需考慮USCQM。

7.3 關于USCQM

由測驗的判準率來看， 不論是長測驗還是短測驗， 在考慮屬性層級結構的情況下， 結構化（最簡）完備Q矩陣可以替代可達陣， 且用題更少， 種類更多; 若不考慮屬性層級結構， 非結構化（最簡）完備Q矩陣也可替代可達陣或單位陣。相對于SSCQM而言， USCQM具有較大應用潛力， 原因有三：第一， 模擬研究發現， 在長測驗中， 含USCQM的判準率大于含可達陣的， 在短測驗中， 雖然USCQM的判準率略低于可達陣， 但相差較小， 約0.03左右（收斂結構差值不超過0.1）， 且其投入產出比均大于可達陣。第二， SSCQM和可達陣是基于屬性層級結構的， 但由于認知過程存在個體差異， 屬性層級結構不一定適合所有作答者。比如， 命題者（熟手）與被試（生手）對相同問題的認知過程不一定相同， 因此專家在設計Q矩陣時是否需要考慮屬性層級結構也持有不同意見， 如K?hn和Chiu （2021）認為遵循某種屬性層級結構不是必要的。第三， USCQM設計更豐富靈活。以收斂結構（a）為例， 介于之間的USCQM 達53個， 而SSCQM僅有2個， 可達陣只有1個。USCQM設計的這一特點， 有助于豐富出題的多樣性， 不僅在紙筆測驗中極具優勢， 而且可以解決CD-CAT中因項目過度曝光帶來的題庫安全等問題。

7.4 關于基于可達陣提取的完備Q矩陣

基于可達陣R提取的多級評分SSCQM有如下優勢：

（2）構造USCQM的關鍵。從R中提取的SSCQM有助于找到對應單位陣中的列， 而在R之外很難找到對應于單位陣中的列， 故而不利于USCQM的構造。

8 結論

針對0-1屬性多級評分Q矩陣設計， 本研究提出了SSCQM和USCQM概念， 并給出了基于可達陣的SSCQM和USCQM設計及其算法。通過模擬研究， 考察屬性層級結構、屬性個數和項目參數等因素對（含）SSCQM、USCQM和可達陣等三種測驗判準率的影響。研究結果均表明：第一， 測驗（含）SSCQM、USCQM和可達陣越多， 則判準率越高。第二， 在長測驗中， 當列數相同時， 隨著項目參數的增加或屬性個數的增加或屬性層級結構的變化（從線型結構到無結構）， 含USCQM測驗的判準率逐漸高于含SSCQM測驗的判準率， 含可達陣測驗的判準率最低。第三， 對于一定條件的長測驗， 當SSCQM/USCQM的列數與可達陣的列數相同或者略少時， 其判準率高于可達陣， 但無論各個因素如何變化， 三種測驗的判準率非常接近。第四， 在項目質量好的短測驗中， 多個SSCQM是最優測驗， 因此要特別注意測驗項目的打磨。第五， 實測數據研究表明， 含SSCQM的測驗和含可達陣的測驗對被試的識別重復率達90%以上， 屬性掌握比例相差不超過7%。總之， 基于理想反應模式， 本文提出的SSCQM和USCQM不僅可以替代可達陣， 而且可增加測驗的多樣性， 降低測驗的曝光率。

9 展望

本研究僅針對0-1屬性多級評分的一種評分方式和滿分值進行了SCQM設計的探討， 為多級評分Q矩陣的設計提供了思路， 而對于其他評分方式和滿分值， SSCQM和USCQM如何構造， 值得研究。相較于0-1水平屬性， 多分屬性因對被試認知能力刻畫更為細致而獲得廣泛關注， 關于多分屬性0-1評分的測驗設計問題（蔡艷， 涂冬波， 2015）， 目前有研究表明擬可達陣使得被試IRP與KS一一對應（丁樹良 等， 2015）， 故擬可達陣為SSCQM， 然而USCQM的構造問題仍未涉及。進一步地， 如何構造多分屬性多級評分的SSCQM和USCQM？從0-1屬性到多分屬性， 從0-1評分到多級評分， 這些因素兩兩結合的Q矩陣設計是否存在某種內在邏輯聯系， 0-1屬性0-1評分的測驗設計是否是多分屬性多級評分測驗設計的特例， 是否可以拓展至多分屬性多級評分？SCQM題量少， 是否適用于類似PISA測試（分配給學生不同且少量的題目測試）的情景中， 未來可進一步驗證與應用。

參 考 文 獻

Cai， Y.， & Tu， D. B. （2015）. Extension of cognitive diagnosis models based on the polytomous attributes framework and their Q-matrices designs. Acta Psychologica Sinica， 47（10）， 1300?1308.

[蔡艷， 涂冬波. （2015）. 屬性多級化的認知診斷模型拓展及其Q矩陣設計. 心理學報， 47（10）， 1300?1308.]

Cai， Y.， Zhao， Y.， Liu， S. C.， Zhang， S. F.， & Tu， D. B. （2017）. An extended polytomous cognitive diagnostic model. Journal of Psychological Science， 40（6）， 1491?1497.

[蔡艷， 趙洋， 劉舒暢， 張淑芳， 涂冬波. （2017）. 一種優化的多級評分認知診斷模型. 心理科學， 40（6）， 1491?1497.]

Chen， J.， & de la Torre， J. （2018）. Introducing the general polytomous diagnosis modeling framework. Frontiers in Psychology， 9. https：//doi.org/10.3389/fpsyg.2018.01474

Chiu， C. Y. （2013）. Statistical refinement of the Q-matrix in cognitive diagnosis. Applied Psychological Measurement， 37（8）， 598?618.

Chiu， C. Y.， Douglas， J.， & Li， X. （2009）. Cluster analysis for cognitive diagnosis： Theory and applications. Psychometrika， 74， 633?665.

Chiu， C. Y.， & K?hn， H. F. （2015）. Consistency of cluster analysis for cognitive diagnosis： The DINO model and the DINA model revisited. Applied Psychological Measurement， 39（6）， 465?479.

De Carlo， L. T. （2011）. On the analysis of fraction subtraction data： The DINA model， classification， latent class sizes， and the q-matrix. Applied Psychological Measurement， 35（1）， 8?26.

De Carlo， L. T. （2012）. Recognizing uncertainty in the Q-matrix via a Bayesian extension of the DINA model. Applied Psychological Measurement， 36（6）， 447?468.

de la Torre， J. （2011）. The Generalized DINA Model Framework. Psychometrika， 76（2）， 179?199.

Ding， S. L.， Luo， F.， & Wang， W. Y. （2014）. Design of polytomous cognitively diagnostic test blueprint——For the independent and the rhombus attribute hierarchies. Journal of Jiangxi Normal University （Natural Sciences Edition）， 38（3）， 265?269.

[丁樹良， 羅芬， 汪文義. （2014）. 多級評分認知診斷測驗藍圖的設計——獨立型和收斂型結構. 江西師范大學學報（自然科學版）， 38（3）， 265?269.]

Ding， S. L.， Luo， F.， Wang， W. Y.， LI， J.， & Xiong， J. H. （2022）. The structure of unstructured complete Q matrices and their identification. Journal of Jiangxi Normal University （Natural Sciences Edition）， 46（5）， 441?446.

[丁樹良， 羅芬， 汪文義， 李佳， 熊建華. （2022）. 非結構化完備Q陣的構造與判定. 江西師范大學學報（自然科學版）， 46（5）， 441?446.]

Ding， S. L.， Luo， F.， Wang， W. Y.， & Xiong， J. H. （2015）. The properties of 0-1 and polytomous Reach ability matrices and their applications. Journal of Jiangxi Normal University （Natural Sciences Edition）， 39（1）， 64?68.

[丁樹良， 羅芬， 汪文義， 熊建華. （2015）. 0-1和多值可達矩陣的性質及應用. 江西師范大學學報（自然科學版）， 39（1）， 64?68.]

Ding， S. L.， Mao， M. M.， Wang， W. Y.， Luo， F.， & Cui， Y. （2012）. Evaluating the consistency of test items relative to the cognitive model for educational cognitive diagnosis. Acta Psychologica Sinica， 44（11）， 1535?1546.

[丁樹良， 毛萌萌， 汪文義， 羅芬， Cui， Y. （2012）. 教育認知診斷測驗與認知模型一致性的評估. 心理學報， 44（11）， 1535?1546.]

Ding， S. L.， Wang， W. Y.， & Luo， F. （2014）. Design of polytomous cognitively diagnostic test blueprint——For the rooted tree type. Journal of Jiangxi Normal University （Natural Sciences Edition）， 38（2）， 111?118.

[丁樹良， 汪文義， 羅芬. （2014）. 多級評分認知診斷測驗藍圖的設計——根樹型結構. 江西師范大學學報（自然科學版）， 38（2）， 111?118.]

Ding， S. L.， Wang， W. Y.， & Yang， S. Q. （2011）. The design of cognitive diagnostic test blueprints. Journal of Psychological Science， 34（2）， 258?265.

[丁樹良， 汪文義， 楊淑群. （2011）. 認知診斷測驗藍圖的設計. 心理科學， 34（2）， 258?265.]

Ding， S. L.， Yang， S. Q.， & Wang， W. Y. （2010）. The importance of reachability matrix in constructing cognitively diagnostic testing. Journal of Jiangxi Normal University （Natural Sciences Edition）， 34（5）， 490?494.

[丁樹良， 楊淑群， 汪文義. （2010）. 可達矩陣在認知診斷測驗編制中的重要作用. 江西師范大學學報（自然科學版）， 34（5）， 490?494.]

Fang， G.， Liu， J.， & Ying， Z. （2019）. On the identifiability of diagnostic classification models. Psychometrika， 84（1）， 19? 40.

Gao， X. L.， Gong， Y.， & Wang， F. （2021）. Research progress in polytomous cognitive diagnosis model. Journal of Psychological Science， 44（2）， 457?464.

[高旭亮， 龔毅， 王芳. （2021）. 多級評分認知診斷模型述評. 心理科學， 44（2）， 457?464.]

Gro?， J.， & George， A. C. （2014）. On permissible attribute classes in noncompensatory cognitive diagnosis models. Methodology： European Journal of Research Methods for the Behavioral and Social Sciences， 10（3）， 100?107.

Gu， Y.， & Xu， G. （2019）. The sufficient and necessary condition for the identifiability and estimability of the DINA model. Psychometrika， 84（2）， 468?483.

Gu， Y.， & Xu， G. （2021a）. Sufficient and necessary conditions for the identifiability of the Q-matrix. Statistica Sinica， 31（1）， 449?472.

Gu， Y.， & Xu， G. （2021b）. Identifiability of hierarchical latent attribute models. preprint arXiv： 1906.07869v4.

Kang， C. H.， Xin， T.， & Tian， W. （2013）. Development and validation of diagnostic test for primary school arithmetic word problems. Examinations Research， 41（6）， 24?43.

[康春花， 辛濤， 田偉. （2013）. 小學數學應用題認知診斷測驗編制及效度驗證. 考試研究， 41（6）， 24?43.]

K?hn， H. F.， & Chiu， C. Y. （2017）. A procedure for assessing the completeness of the Q-matrices of cognitively diagnostic tests. Psychometrika， 82， 112?132.

K?hn， H. F.， & Chiu， C. Y. （2021）. A unified theory of the completeness of Q-Matrices for the DINA model. Journal of Classification， 38（3）， 500?518.

Leighton， J. P.， & Gierl， M. J. （2007）. Cognitive diagnostic assessment for education： Theory and applications. Cambridge University Press.

Lin， M.， & Xu， G. （2023）. Sufficient and Necessary Conditions for the Identifiability of DINA Models with Polytomous Responses. preprint arXiv： 2304.01363.

Liu， J.， Xu， G.， & Ying， Z. （2012）. Data-driven learning of Q-matrix. Applied Psychological Measurement， 36（7）， 548? 564.

Liu， J.， Xu， G.， & Ying， Z. （2013）. Theory of the self-learning Q-matrix. Bernoulli， 19， 1790?1817.

Ma， W. C.， & de la Torre， J. （2016）. A sequential cognitive diagnosis model for polytomous responses. British Journal of Mathematical and Statistical Psychology， 69（3）， 253?275.

Madison， M. J.， & Bradshaw， L. P. （2015）. The effects of Q-matrix design on classification accuracy in the log-linear cognitive diagnosis model. Educational and Psychological Measurement， 75（3）， 491?511.

Ouyang， J.， & Xu， G. （2022）. Identifiability of latent class models with covariates. Psychometrika， 87（4）， 1343?1360.

Sun， J. N.， Xin， T.， Zhang， S. M.， & de la Torre， J. （2013）. A polytomous extension of the generalized distance discriminating method. Applied Psychological Measurement， 37（7）， 503?521.

Tatsuoka， K. K. （1995）. Architecture of knowledge structures and cognitive diagnosis： A statistical pattern recognition and classification approach. Erlbaum： Hillsdale， 327?359.

Tatsuoka， K. K. （2009）. Cognitive assessment： An introduction to the rule space method. Routledge/Taylor & Francis Group.

Xu， G.， & Zhang， S. （2016）. Identifiability of diagnostic classification models. Psychometrika， 81（3）， 625?649.

Design of the polytomous simplest complete Q matrix based on the reachability matrix

Abstract

The identifiability of cognitive diagnosis models relies heavily on the completeness of the Q matrix. However， existing test designs primarily focus on dichotomously-scored items， neglecting the importance of polytomous cognitive diagnostic test design. Moreover， this limitation poses a significant obstacle to the advancement of cognitive diagnosis. To bridge this gap， this paper aimed to introduce novel designs for the construction of polytomous structured and unstructured simplest complete Q matrices （SSCQM/USCQM）. Our proposed approach considered all ideal response patterns （IRPs） of knowledge states （KSs） on the reachability matrix as research objects， with the objective of minimizing the number of columns selected from the reachability matrix. This ensured one-to-one correspondence between the set of KSs and the set of IRPs， thereby enhancing the completeness of the SSCQM. Additionally， we derived a polytomous USCQM by considering the relationship between the SSCQM and the sub-matrix of the corresponding identity matrix while ensuring that each row contains at least one “1”. Interestingly， the construction process revealed that there were more USCQMs than SSCQMs. This innovative approach expanded the possibilities for polytomous cognitive diagnostic test design.

This study focused on the design and evaluation of cognitive diagnostic tests using polytomous structured and unstructured Q matrices （SSCQM/USCQM）. We conducted two studies to comprehensively examine the influence of factors such as the number of attributes， attribute hierarchies， and item parameters on the precision of the SSCQM， USCQM， and reachability matrix. In the first study， variations in attribute structures and item parameter values were investigated to understand their impact on Q matrix accuracy. On the other hand， the second study explored the effects of attribute hierarchies and the number of attributes on the precision of the SSCQM， USCQM， and reachability matrix.

Both simulation studies and actual measurement data were utilized to assess the robustness and efficacy of the two methods. Firstly， the simulation results revealed several key findings. Notably， increasing the number of SSCQMs or USCQMs positively influenced the accuracy of the results. In the context of long tests， the USCQM demonstrated higher Pattern Match Ratio （PMR） and Marginal Match Ratio （MMR） compared to the SSCQM and the reachability matrix. This trend was particularly evident when there was an increase in item parameters， attribute numbers， or a change in attribute hierarchy. However， it is noteworthy that， regardless of these various factors， the PMR and MMR of the three tests exhibited minimal differences. On the other hand， in short tests with good item quality， the SSCQM achieved the best performance compared to other methods. This highlights the importance of considering specific test characteristics and item quality when selecting the appropriate Q matrix type. These findings provide valuable insights into the factors that influence the precision of Q matrices. They emphasize the benefits of increasing the number of matrices， understanding the impact of item parameters， and recognizing the performance disparities among different matrix types. Obtaining a comprehensive understanding of these relationships is vital for optimizing the design and implementation of cognitive diagnostic testing， ultimately guaranteeing accurate assessments of individual knowledge states. Secondly， analysis of the actual measurement data showed high identification repetition rates for the SSCQM and the reachability matrix， with a minimal difference in attribute mastery ratio.

In summary， both the SSCQM and the USCQM demonstrate adequate performance when compared to other Q matrices under similar conditions. These findings emphasize the significance of prioritizing completeness in cognitive diagnostic testing. This research seeks to contribute to the advancement of cognitive diagnosis by addressing the limitations of existing test designs and introducing new techniques for constructing polytomous Q matrices. In addition， the findings presented in this paper offer valuable insights for researchers and practitioners seeking to design high-quality cognitive diagnostic tests that accurately assess individual knowledge states.

Keywords polytomous， test design， SSCQM， USCQM， algorithm

附錄

基本屬性層級結構及其他結構的結構化最簡完備Q矩陣算法步驟

第二步首先從最后1列開始， 第6列大于前面的列， 將第6列放入Q1中， 并在W中刪除此列; 再考慮第5列， 情況如同第6列， 把該列放入Q1中， 并在W中刪除此列， 如此下去， 直至把第3列放入Q1中， 此時剩余列數等于2， 直接計算W 剩余列的支柱列; 接著由于此時W中第2列大于第1列， 刪除第1列， 將第2列放入Q2中;

第三步計算Q1支柱列， 最大列為全1列;

第四步由屬性層級結構的分支數為1， 則只取Q1中全1列為結構化的Q矩陣;

第五步驗證全1列為結構化最簡完備Q矩陣。

收斂型（a）：第一步將可達陣中項目依據列和從小到大進行排序， 由第4列和第5列的列和相同， 則有

第二步首先兩矩陣的第6列均大于前面的列， 則將第6列放入Q1中， 并在和中刪除此列; 接著計算和剩余列的支柱列， 和的第1列小于第2列， 第2列小于第3列， 第3列小于第4列， 將第1，2，3列刪除， 第4列放入Q2中， 最后重置和， 原第5列為新第1列， 因只剩1列， 直接放入Q2中;

第三步 Q1只有1列， 故該列為支柱列;

第四步該屬性層級結構圖中有2個分支， 故從Q2中隨機取1列， 與Q1合并為一個矩陣， 故總共2個矩陣， 為

第二步首先兩矩陣的第6列均大于前面的列， 則將第6列放入Q1中， 并在和中刪除此列; 接著計算和剩余列的支柱列， 的第1列小于第2列， 第2列與第3列不能比較， 第2列小于第4列， 第4列小于第5列， 將第1，2，4列刪除， 第5列放入Q2中， 最后重置， 原第3列為新第1列， 因只剩1列， 直接放入Q2中， 此時Q1有1列， 為（1，1，1，1，1，1）T， Q2有2列， 為（1，1，0，0，0，0）T和（1，0，1，1，1，0）T; 的第1列小于第2列， 第2列與后面的列均不可比較， 將第1列刪除， 第2列放入Q2中， 重置的列， 原來的第3，4，5列即為新的第1，2，3列， 第3列大于第1，2列， 則將第3列放入Q1中， 因此的列數為2列， 第2列大于第1列， 刪除第1列， 將第2列放入Q2中， 此時Q1有2列， 為（1，1，1，1，1，1）T和（1，0，1，1，1，0）T， Q2有2列， 為（1，1，0，0，0，0）T和（1，0，1，1，0，0）T;

第三步 的Q1只有2列， 取最大列 （1，1，1，1，1，1）T為支柱列;

第四步該屬性層級結構圖中有2個分支， 故從和Q2中隨機取1列， 與和的Q1支柱列合并為一個矩陣， 故總共4個矩陣， 為

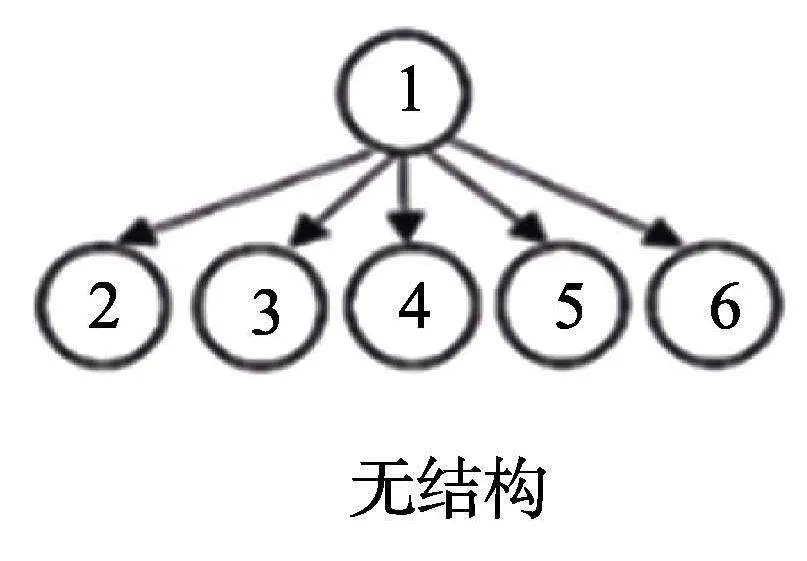
分支型：第一步將可達陣中項目依據列和從小到大進行排序， 由第2列和第3列， 第4列、第5列和第六列的列和相同， 則有;

第二步首先中沒有最大列， 故Q1為空; 接著計算的支柱列， 的第1列小于第2列， 第2列小于第4列， 將第1，2列刪除， 第4列放入Q2中， 重置， 原第3，5，6列為新第1，2，3列， 第1列小于第2列， 第2列與第3列不能比較， 將第1列刪除， 第2列放入Q2中， 重置， 剩余1列， 也放入Q2中;

第三步 Q1為空;

第四步該屬性層級結構圖中有3個分支， 故Q2正好3列， 矩陣即為所求;

第五步驗證所得矩陣為結構化最簡完備Q矩陣。的結論一致。

無結構：第一步將可達陣中項目依據列和從小到大進行排序， 由第2列至第6列的列和相同， 則將這些列進行全排列， 以其中為例;

第二步首先中沒有最大列， 故Q1為空; 接著計算的支柱列， 的第1列小于第2列， 第2列與后面列均不可比較， 將第1列刪除， 第2列放入Q2中， 重置， 新的列均不能比較， 全部放入Q2中（無論列和為2的列如何排列， 這些列均互相不可比較， 故結果一致）;

第三步 Q1為空;

第五步驗證所得矩陣為結構化最簡完備Q矩陣。

第二步首先Q1為空; 接著計算的支柱列， 的列均不能比較， 全部放入Q2中（無論列和為1的列如何排列， 這些列均互相不可比較， 故結果一致）;

第三步 Q1為空;

第五步驗證所得矩陣為結構化最簡完備Q矩陣。

其他結構：

Sun等人（2013）文章中的結構

第一步將可達陣中項目依據列和從小到大進行排序， 由第1列至第4列， 第5， 6列的列和相同， 則將這些列分別全排列， 以其中為例;

第二步首先的第7列均大于前面的列， 則將第7列放入Q1中， 并在中刪除此列; 接著計算的支柱列， 的第1列與第2，3，4列不能比較， 小于第5列， 將第1列刪除， 第5列放入Q2中， 重置， 原第2，3，4，6列為新第1，2，3，4列， 此時沒有最大列， 第1列無法比較， 放入Q2中， 并在中刪除， 重置， 第2，3，4列為第1，2，3列， 也即原第3，4，6列， 這時的第3列最大， 放入Q1中， 第1，2列不能比較， 均放入Q2中， 此時Q1有2列， 為（1，1，1，1，1，1，1）T和（0，0，0，1，1，1，0）T， Q2有4列， 為（1，1，1，0，0，0，0）T 、（0，1，0，0，0，0，0）T、（0，0，0，1，0，0，0）T和（0，0，0，0，1，0，0）T;

第三步 Q1有2列， 取大為（1，1，1，1，1，1，1）T;

第五步驗證所得矩陣為結構化最簡完備Q矩陣。其他矩陣可得到其他6種結構化最簡完備Q矩陣。

K?hn和Chiu （2021） 文章中的結構

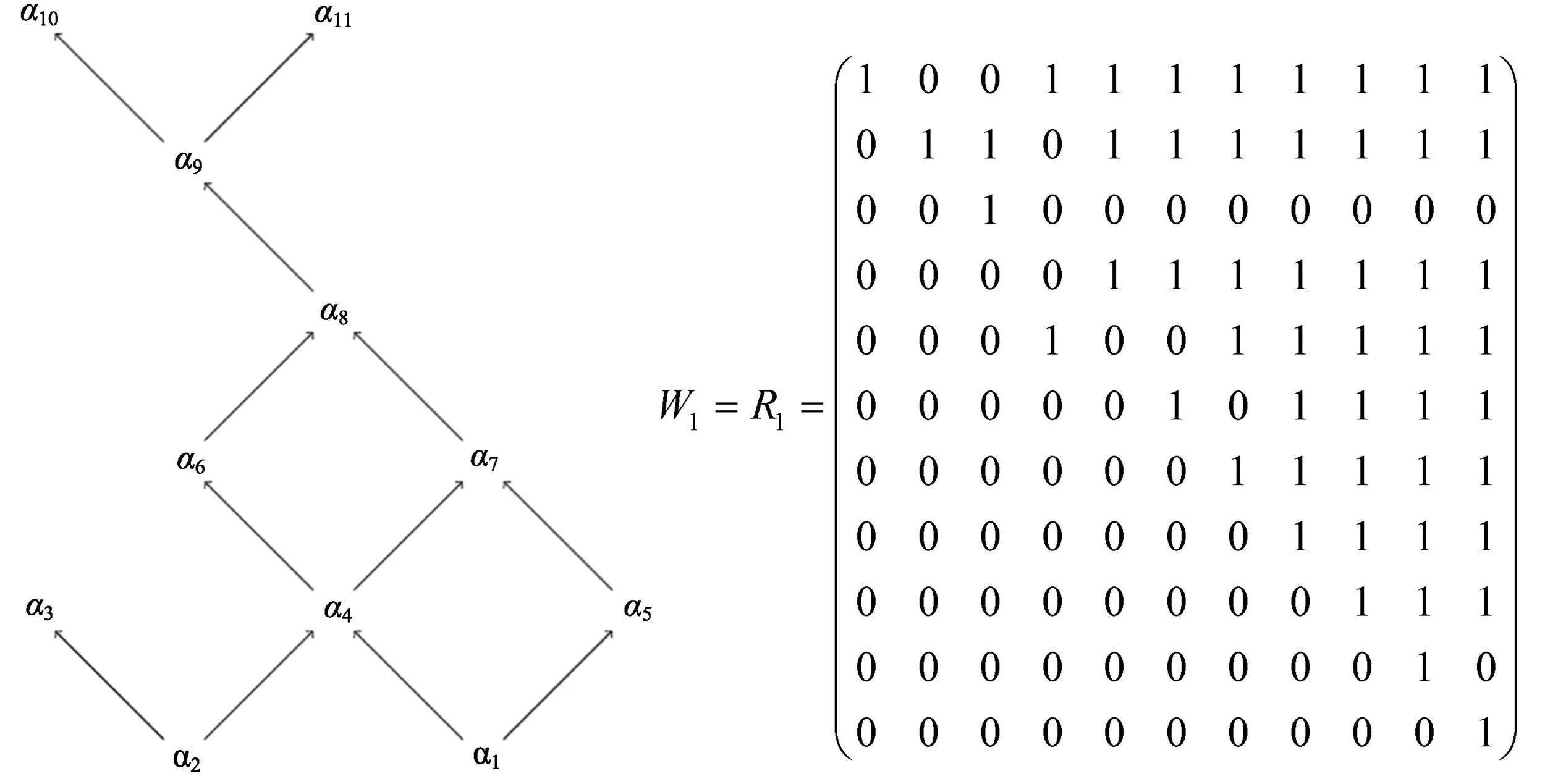
第一步將可達陣中項目依據列和從小到大進行排序， 由兩對列和相同， 則全排列， 以為例;

第二步首先中沒有最大列， 故Q1為空; 接著計算的支柱列， 的第1列小于第4列， 第4列小于第7列， 第7，8，9，10列依次增大， 將第1，4，7，8，9列刪除， 第10列放入Q2中， 重置， 沒有最大列， 原第2列小于第3列， 第3列與其他列不能比較， 將第2列刪除， 第3列放入Q2中， 重置， 原第11列最大， 放入Q1中， 剩余原5，6列， 由第5列小于第6列， 刪除第5列， 第6列放入Q2中， 故Q1中只有原第11列， Q2中有原第3，6，10列;

第三步 Q1中只有原第11列;

第四步該屬性層級結構圖中的分支無法計算， 隨機從 Q2中分別取1列、2列、3列與Q1中的列組合成矩陣Q;

第五步驗證矩陣Q只有包含第3，6，10，11列即為結構最簡化完備Q矩陣。

2.5個屬性四種屬性層級結構

7個屬性四種屬性層級結構

8個屬性四種屬性層級結構