力學臨界極值問題的三種常見解法

【摘要】高中物理問題的解答要求學生擅長通過分析“題眼”找到問題突破口，繼而高效率地解題.其中“最大”“最小”“恰好”都是常見的題眼，也對應一類臨界問題.解答臨界極值問題具有一定方法，常見的有極限法、圖解法、解析法.掌握常見解決方法，有助于學生理清題意，提高解題效率.

【關鍵詞】臨界問題；高中物理；解題方法

高中物理中的臨界極值問題是高考的高頻考點.以力學的臨界問題為范例，本文主要從解題方法層面分析不同思路的特點和適用范圍，旨在幫助學生更快速地分析求解問題.

1 極限法

極限法求解臨界問題，主要思路在于把問題條件推向極端條件，需要注意的是分析受力或運動是個動態過程，必要時應把其中的物理量放大或縮小找到其中的臨界狀態，才能解決問題.

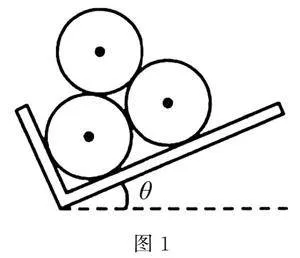
例1 課堂上，老師準備了“L”形光滑木板和三個完全相同、外表面光滑的勻質圓柱形積木，要將三個積木按圖1所示（截面圖）方式堆放在木板上，則木板與水平面夾角θ的最大值為（ ）

（A）30°. （B）45°. （C）60°. （D）90°.

分析 解答該題需要對木板與地面形成的角度θ這一物理量進行放大或縮小，由于問題求解積木堆積時角度的最大值，故放大得到動態情況，可知最上面的圓形積木與左下積木重疊時最上面積木會落在地面，即將積木滑動落下對應θ的最大值，求解出來即可.

解 當最上面積木的重心與左下方積木的重心在同一豎直線上時，最上面積木即將滾動，此時木板與水平面夾角θ達到最大，根據幾何關系可得，θ的最大值為30°.

故正確答案為選項（A）.

2 圖解法

圖解法適用于大部分力學問題，解題關鍵在于得到受力分析圖，用幾何圖形運動情境，再求對應的臨界值大小.在求解過程中，需要正確畫出物體的受力分析圖，并找出所求臨界值物理量在圖象中對應的線段或面積，其次根據幾何圖形性質求解.

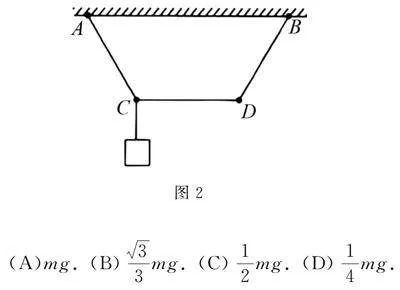
例2 如圖2所示，三根長度均為L的輕繩分別連接于C、D兩點，A、B兩端被懸掛在水平天花板上，相距2L.現在C點上懸掛一個質量為m的重物，重力加速度大小為g，為使CD繩保持水平，在D點上可施加力F的最小值為（ ）

（A）mg. （B）33mg. （C）12mg. （D）14mg.

分析 首先需要對節點C、節點D做受力分析，節點D分別受到繩CD的水平拉力、繩BD的拉力、施加的外力F，得到受力分析圖后，通過正交分解使所有力形成矢量三角形，根據垂線段最短得到最小值.

解 由題意可知，CD繩保持水平必須使各繩繃緊，

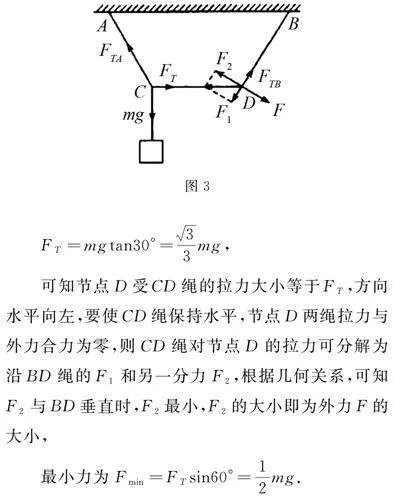
則AC與水平方向的夾角為60°，節點C受力平衡，如圖3所示，

FT=mgtan30°=33mg，

可知節點D受CD繩的拉力大小等于FT，方向水平向左，要使CD繩保持水平，節點D兩繩拉力與外力合力為零，則CD繩對節點D的拉力可分解為沿BD繩的F1和另一分力F2，根據幾何關系，可知F2與BD垂直時，F2最小，F2的大小即為外力F的大小，

最小力為Fmin=FTsin60°=12mg.

故正確答案為選項（C）.

3 解析法

解析法具體指所求物理量等價轉化為數學公式，運用表達式求最值.運用該方法能解答大部分問題，結合公式列出與所求物理量有關的等式，最后運算解答即可.

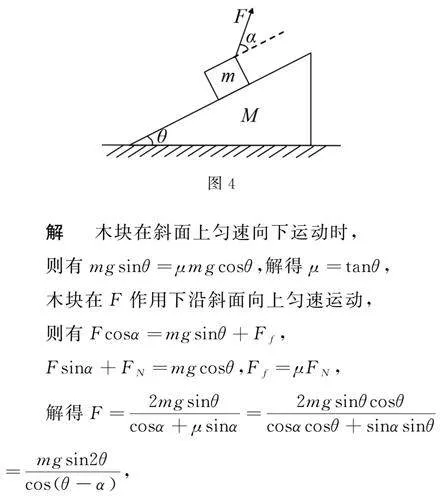
例3 如圖4所示，質量為M的斜面傾角為θ，在水平面上保持靜止，當將一質量為m的木塊放在斜面上，正好勻速下滑.如果用與斜面角度為α的力F拉木塊，木塊能勻速上升，已知斜面在整個過程中始終靜止，當α多大時，F有最小值，求此時α的大小及F的最小值？

分析 本題是兩個未知物理量牽連變化的問題，需要將角度α看作自變量，施加的外力F為因變量，構造函數解析式，分析函數對應的最小值.

解 木塊在斜面上勻速向下運動時，

則有mgsinθ=μmgcosθ，解得μ=tanθ，

木塊在F作用下沿斜面向上勻速運動，

則有Fcosα=mgsinθ+Ff，

Fsinα+FN=mgcosθ，Ff=μFN，

解得F=2mgsinθcosα+μsinα=2mgsinθcosθcosαcosθ+sinαsinθ=mgsin2θcosθ－α，

當α=θ時，F有最小值，Fmin=mgsin2θ.

4 結語

上述例題分別對高中物理力學臨界極值問題的三種求解思路做出具體分析和解讀，不難發現這些方法都有對應的適用范圍和特點.解析法著重運用公式得到臨界值，圖解法則需要結合幾何圖形對其進行分解找到臨界狀態，極限法則通過放大或縮小物理量的思路找到動態過程中狀態變化的臨界點.這些方法各有特長，都是學生必須學習和掌握的解題方法.

參考文獻：

[1]謝文杰.對高中物理常見力學臨界問題的分析[J].文理導航，2019（02）：56.

[2]鄧賢彬.探析高中物理力學中的臨界與極值問題[J].中學物理，2021，39（03）：57-59.

[3]張俊凱.淺談高中物理力學中幾種常見的臨界問題[J].教師，2016（18）：104.