永磁同步直線電機位移誤差的預設性能反步控制策略

摘 要：

單軸電機的伺服控制主要是對位移跟蹤精度的控制，誤差較大意味著跟隨效果較差。目前對電機位移誤差的控制策略大多難以做到定量的約束控制。本文提出一種將位移誤差設置在預期范圍內的預設性能反步控制策略，來定量調控輸出位移誤差的響應時間以及超調量等暫態性能，降低直線電機的位移誤差。本文設計了預設性能函數作為控制邊界，保證位移跟蹤誤差處于誤差范圍內并按設定時間快速收斂，利用Lyapunov理論設計反步控制器保證了系統的閉環穩定性和跟蹤誤差的收斂性。最后，利用直線電機伺服實驗平臺，通過不同工況高精度點位運動實驗，證明了該控制算法能夠有效降低點位運動的位置跟隨誤差。

關鍵詞：永磁同步直線電機；預設性能；反步法；誤差轉換；有限時間；位移誤差

DOI：10.15938/j.emc.2024.09.007

中圖分類號：TM921

文獻標志碼：A

文章編號：1007-449X（2024）09-0070-11

收稿日期： 2023-09-15

基金項目：中央引導地方科技發展資金項目（226Z1805G）;天津市自然科學基金（20JCYBJC00730）

作者簡介：滕子鋮（1998—），男，碩士研究生，研究方向為電機控制；

陶友瑞（1973—），男，博士，教授，研究方向為先進復合材料制備技術與工程應用；

李珊瑚（1985—），女，博士，教授，研究方向為電機控制、矩陣變換器；

劉 旭（1984—），男，博士，教授，研究方向為電機控制。

通信作者：李珊瑚

Prescribed performance backstepping control strategy for displacement error of permanent magnet linear synchronous motor

TENG Zicheng1，2， TAO Yourui1， LI Shanhu1，2， LIU Xu1，2

（1.State Key Laboratory of Reliability and Intelligence of Electrical Equipment， Hebei University of Technology， Tianjin 300130， China; 2.Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province， Hebei University of Technology， Tianjin 300130， China）

Abstract：

The servo control of the single-axis motor is mainly to control the displacement tracking accuracy， and the large error means that the tracking effect is poor. At present， most of the control strategies for motor displacement error are difficult to achieve quantitative constraint control. A prescribed performance backstepping control strategy was proposed to set the displacement error within the expected range， so as to quantitatively control the response time of the output displacement error and the transient performance such as overshoot， so as to reduce the displacement error of the linear motor. A prescribed performance function was designed as the control boundary to ensure that the displacement tracking error is within the error range and converges quickly according to the set time， and the Lyapunov theory was used to design the backstepping controller to ensure the closed-loop stability of the system and the convergence of the tracking error. Finally， the linear motor servo experimental platform was used to prove that the control strategy can effectively reduce the position tracking error of point motion through high-precision point motion experiments under different working conditions.

Keywords：permanent magnet linear synchronous motor; prescribed performance; backstepping control; error conversion; finite time; displacement error

0 引 言

永磁直線同步電機（permanent magnet linear synchronous motor，PMLSM）結構簡單、精度高且無傳動機構［1］，近年來在高精密制造設備的伺服驅動上得到了廣泛應用，如XY平臺驅動、數控機床和機器人控制等［2-4］。

在基于永磁直線電機的伺服系統控制方法中，基于PI的二自由度控制雖然擁有結構簡單、參數整定快、易于實現等優點［5］，但是在高速高精度定位平臺中，其位移跟隨誤差往往達不到定位精度的要求。同時外界擾動和模型的不確定性更使得基于PI的二自由度控制策略的魯棒性較差，位置跟隨誤差無法達到更高的精度要求。

為減小不確定性以及外界干擾對輸出位移跟隨誤差造成的影響，國內外研究者提出了許多滑模控制［6-7］、自適應控制［8-9］等諸多非線性控制方法。滑模控制利用不確定性系統的邊界條件設計切變控制律，系統的動態由設計的滑模面決定，與不確定性無關，但是滑模控制中的“抖振”現象給滑模變結構控制在實際系統應用中帶來了困難。文獻［10］提出一種多周期迭代滑模控制算法用于提高直線電機的控制精度，能夠對直線電機受到的多周期干擾進行抑制，但其算法較為復雜。文獻［11］提出一種改進多輸入多輸出無模型自適應控制的二維直線電機迭代學習控制復合控制方案，補償系統非線性因素，前饋反饋優勢互補，但是自適應控制器設計復雜，對系統的實時控制有較長的運行時間，無法保證參數估計值到實際值的漸進收斂。

反步控制［12］（backstepping control，BSC）則是一種靜態補償思想，通過后面子系統中的虛擬控制實現前面子系統的穩定收斂，通過不斷遞推迭代構造李雅普諾夫能量函數進行控制器設計。反步控制方法有很多優點，如魯棒性強、需要調試的參數較少，因而被廣泛應用于電機控制系統中［13-17］。文獻［13］創造性地將反步法應用于電機控制系統；文獻［14］則將滑模控制與反步控制相結合，設計的滑模反步控制器，能有效提高伺服系統的魯棒性；文獻［15］考慮了電機負載擾動，提出了基于反步法的PMSM速度環自適應控制；文獻［16］利用非線性積分反步法設計了自適應積分反步控制器，不僅可以補償參數不確定性的影響，抗負載擾動能力也大大提高，但是自適應控制器設計依舊復雜，對系統的實時控制的運行時間依舊較長。文獻［17］加入周期性學習算法，設計了一種自適應反步滑模控制器保證直線電機的定位精度，但加入的學習算法也提高了控制器的計算量。這些控制策略都結合了反步控制方法，在電機的穩態性能和魯棒性方面都有較好效果，但在暫態性能方面難以做到定量控制，有一定的局限性。

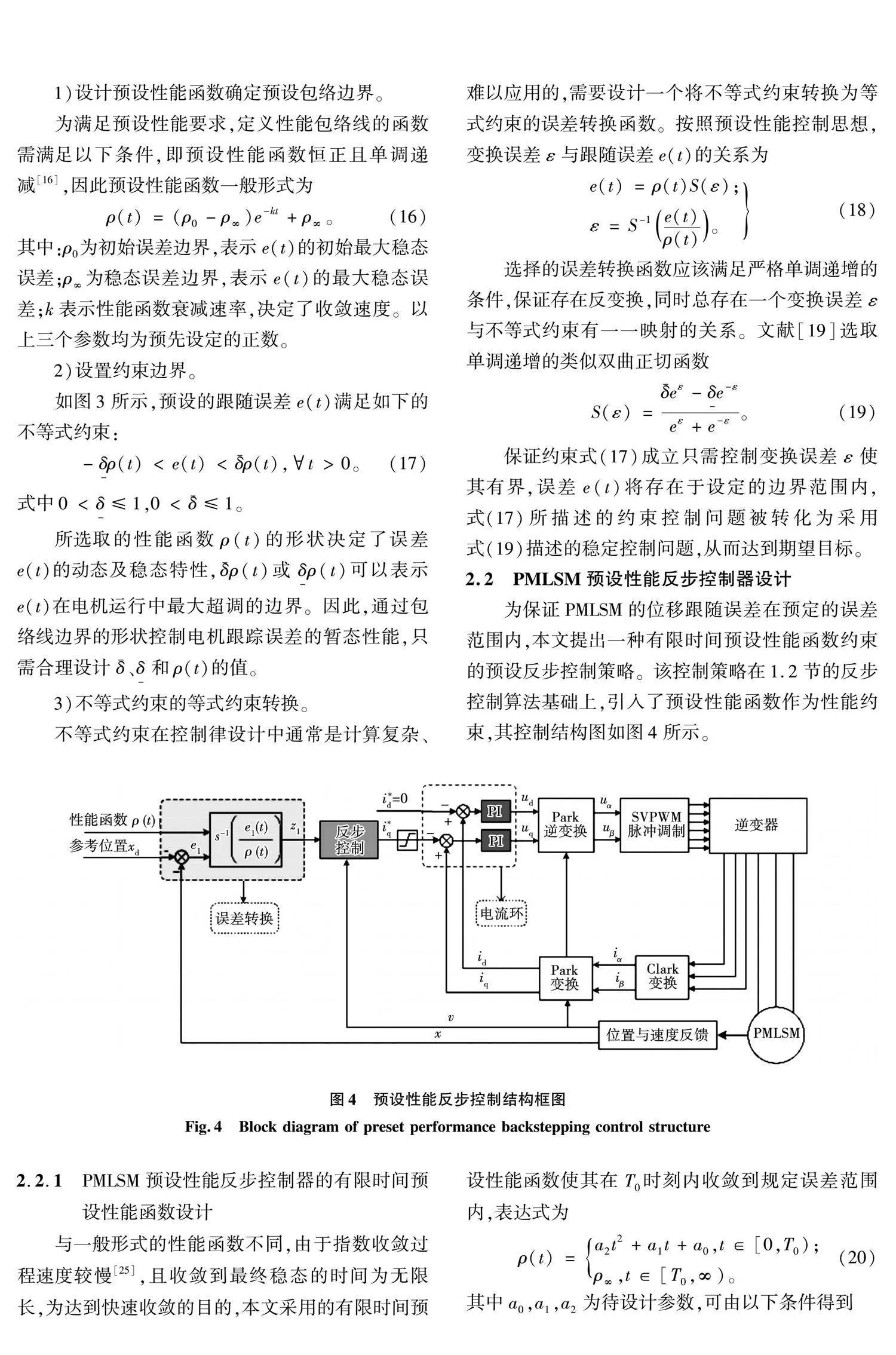
Bechlioulis和Rovithakis于2008年首次提出預設性能函數（prescribed performance control，PPC）［18-19］控制方法，該預設性能控制方法可以預先設定一個邊界函數限制收斂速度及超調量，繼而使跟蹤誤差收斂到一個提前設定好的區域內。這種方法不僅可以保證系統穩定，在系統的暫態特性方面還有較好的控制效果。文獻［20］提出了一種保預設性能魯棒自適應控制方案， 利用自適應投影算法對有界時變參數進行辨識，進行了控制器設計。文獻［21-23］將預設性能引入到常規反步法中，對解決非線性系統的控制問題有很大幫助，主要應用于編隊控制［21］、飛行器飛行控制［22］、汽車懸架控制［23］的位置跟蹤問題。此外，文獻［24］將預設性能引入到自適應控制中，應用于轉臺伺服系統中。

對單軸電機而言，實時的伺服控制主要是跟蹤精度的控制，位移誤差嚴重影響電機運動過程中的精度，在高速高精高加工場合，誤差超限將導致機床振動、零件表面質量惡化、電機失控等嚴重后果，直接影響零件加工質量以及產品要求。目前對于電機的位移誤差難以做到定量的約束控制，同時當前預設性能主要應用在機械控制領域，關于直線電機降低位移誤差的應用較少。

針對上述永磁直線電機跟隨誤差控制方法誤差收斂不確定問題，本文通過結合預設性能控制思想，提出一種在有限時間內快速收斂的預設性能反步控制策略（prescribed performance backstepping control，PPBC），可以定量調控輸出的響應時間以及超調量等暫態性能，與一般的預設性能函數相比，它的收斂速度更快；此外目前伺服行業考慮到成本以及便于擴展，早已將電流環集成在驅動器中，本文保留采用PI控制器的電流環，更廣泛應用于直線電機中，避免反步控制中的微分爆炸，對電機暫態特性有較好控制效果。

1 傳統反步控制策略

1.1 反步控制原理

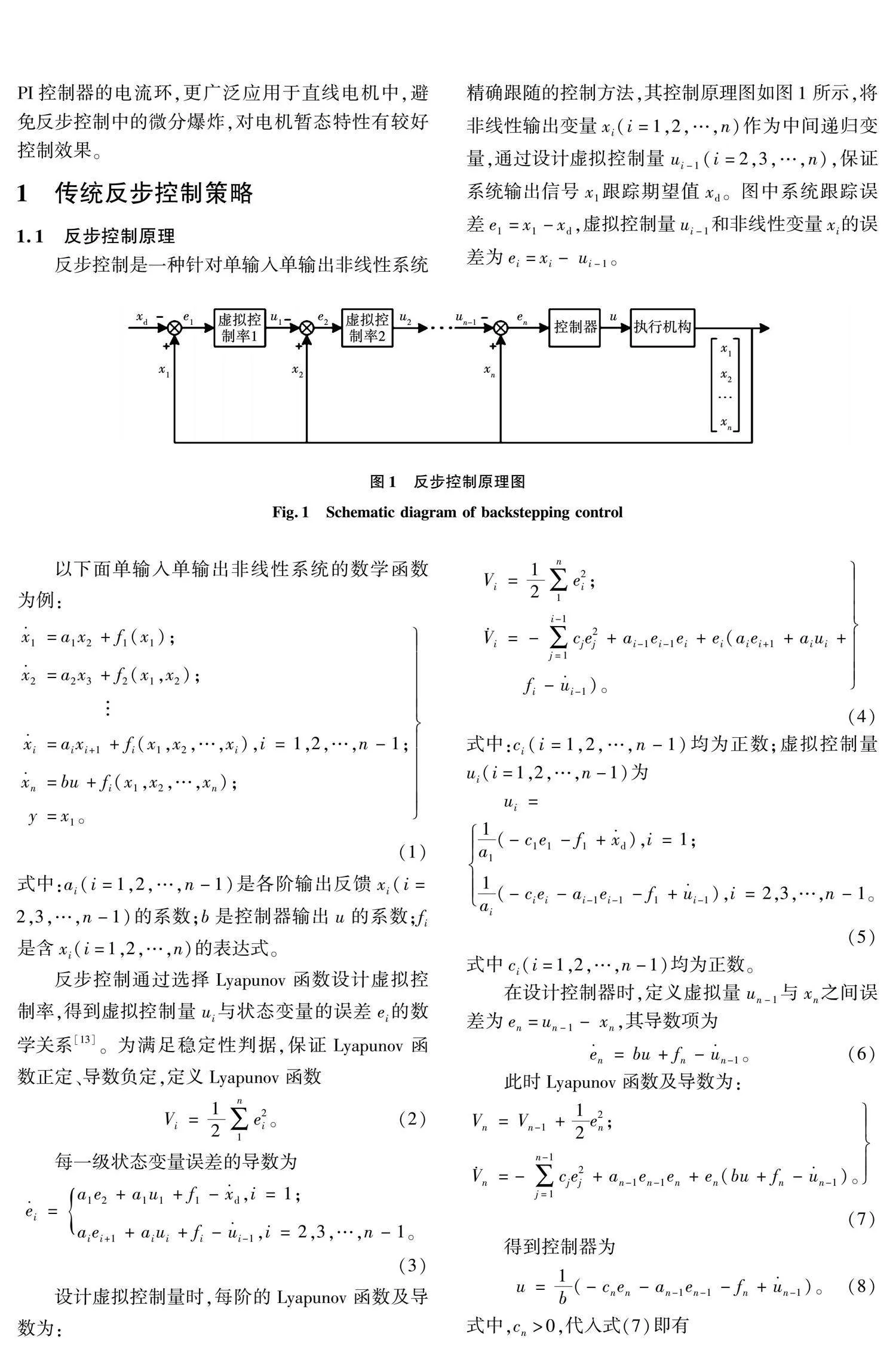
反步控制是一種針對單輸入單輸出非線性系統精確跟隨的控制方法，其控制原理圖如圖1所示，將非線性輸出變量xi（i=1，2，…，n）作為中間遞歸變量，通過設計虛擬控制量ui-1（i=2，3，…，n），保證系統輸出信號x1跟蹤期望值xd。圖中系統跟蹤誤差e1=x1-xd ，虛擬控制量ui-1和非線性變量xi的誤差為ei=xi- ui-1。

3 仿真與實驗

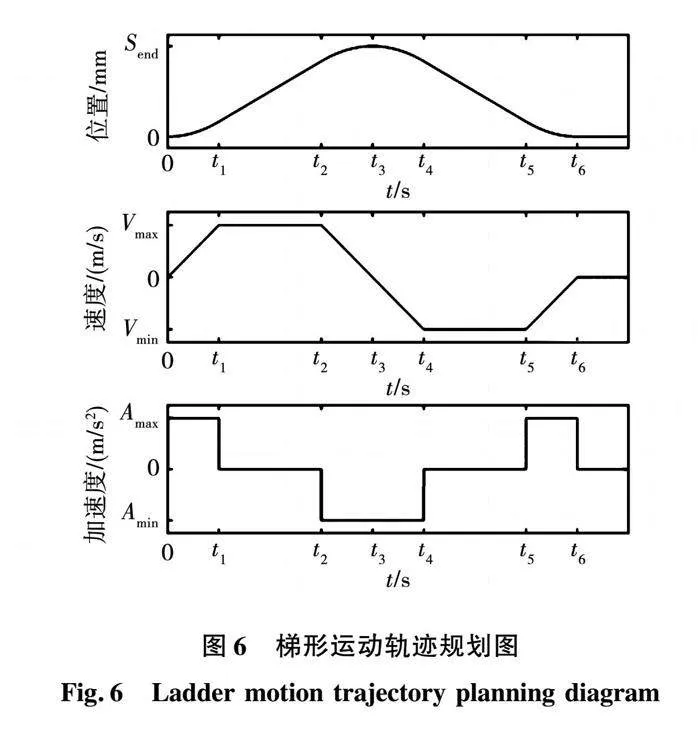
在如芯片封裝點膠過程中，點膠工藝主要為點膠（定位運動）和涂膠（輪廓運動），單軸電機跟蹤精度的位移誤差需要控制在微米級別。在點膠過程中，點膠直線電機通常采用閉環控制的方式，主要用于點到點的高速高精度運動，本文按照時間最短、沖擊最小的原則選擇梯形運動軌跡為參考位移軌跡。該梯形運動軌跡整個往返運動過程可劃分為勻加速階段［0，t1］ ［t5，t6］、勻速階段［t1，t2］ ［t4，t5］和勻減速階段［t2，t4］，如圖6所示。

圖6中：Send為往返運動最大位移；Vmax、Vmin分別為最大速度和最小速度；Amax、Amin分別為最大加速度、最小加速度。

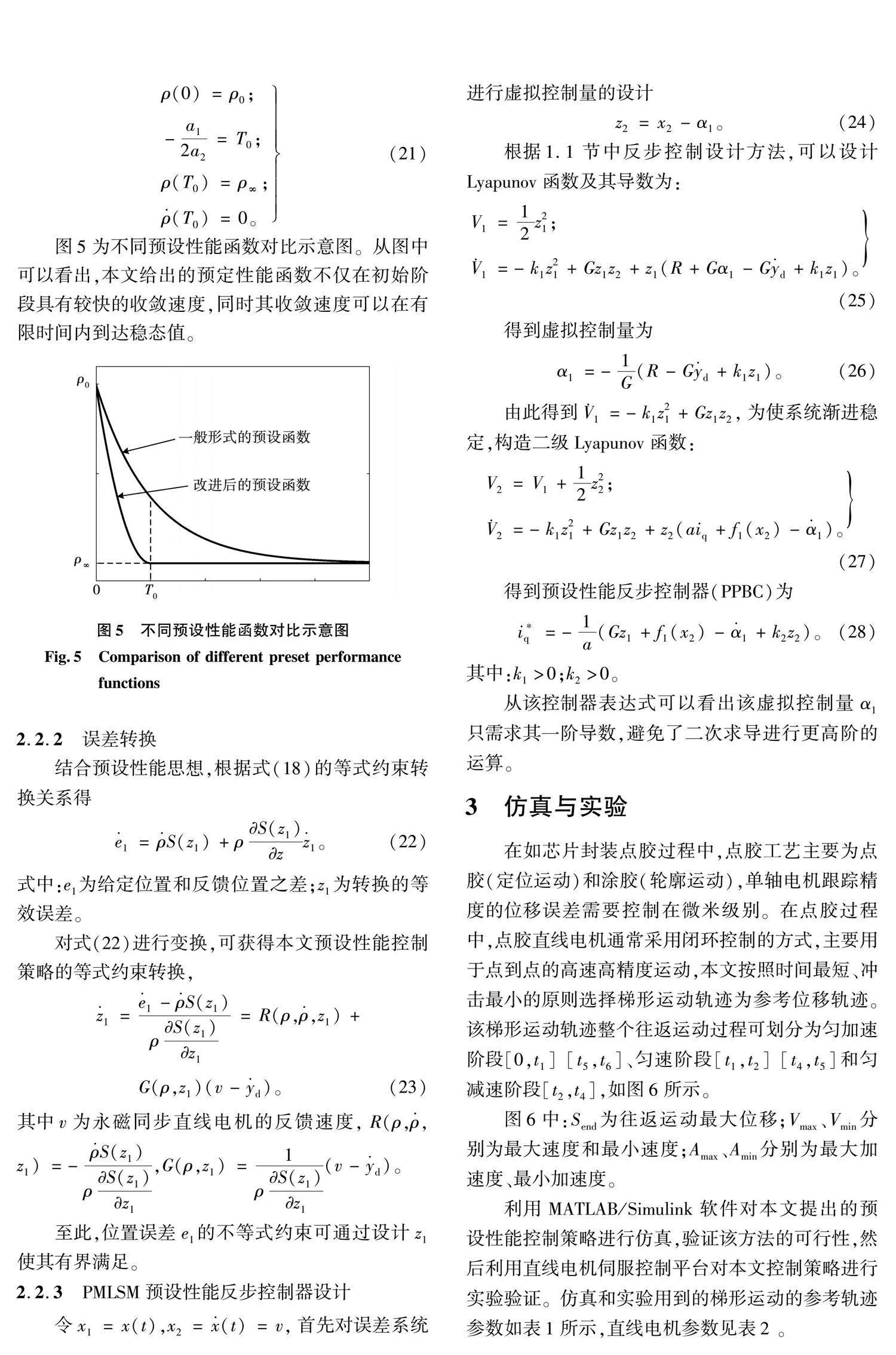
利用MATLAB/Simulink軟件對本文提出的預設性能控制策略進行仿真，驗證該方法的可行性，然后利用直線電機伺服控制平臺對本文控制策略進行實驗驗證。仿真和實驗用到的梯形運動的參考軌跡參數如表1所示，直線電機參數見表2 。

3.1 仿真結果

實際點膠工藝測試中的直線電機伺服系統電流環集成于驅動器中。為驗證提出方法的可行性，預設性能反步控制PPBC、傳統反步控制BSC策略均保留PI電流環，對圖2、圖4的控制方法進行仿真驗證。

電流環的參數設計考慮環路帶寬設計指標，均設計為Kp=330，Ki=1 476，主要優化目標為位移誤差均方根值最小和最大誤差最小。以優化目標為主導，PI策略中，速度控制器的Kp=255、Ki=800，位置控制器的Kp =250；BSC策略根據式（15）設置的控制參數k1=550，k2=2 500；PPBC策略根據式（26）和式（28）設置的控制參數k1=250，k2=850。預設性能函數PPF參數設計為a0=0.001，a1=-0.099，a2=2.475，最終收斂的誤差帶設置為10 μm，轉換函數中上下限分別設置為10-6和10-7。

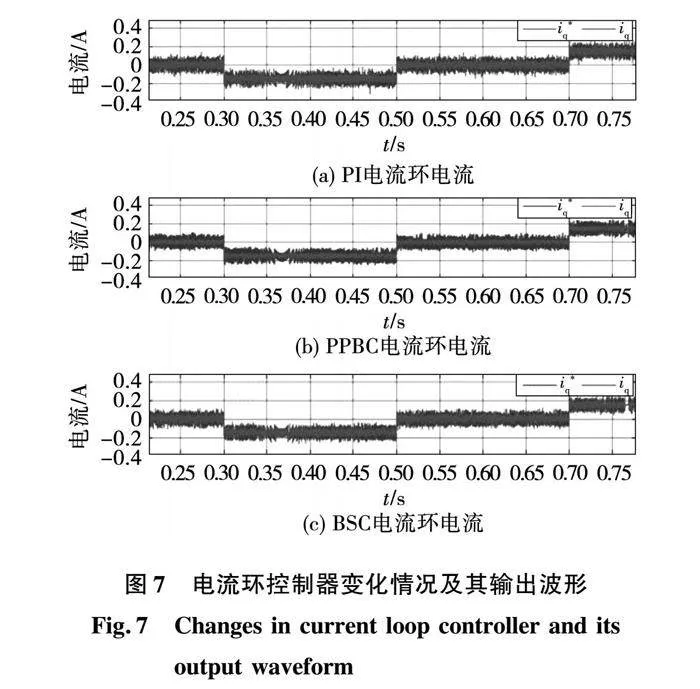
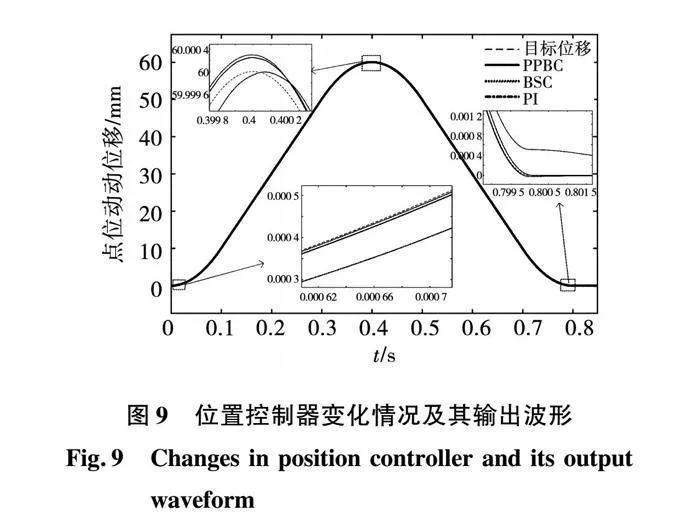
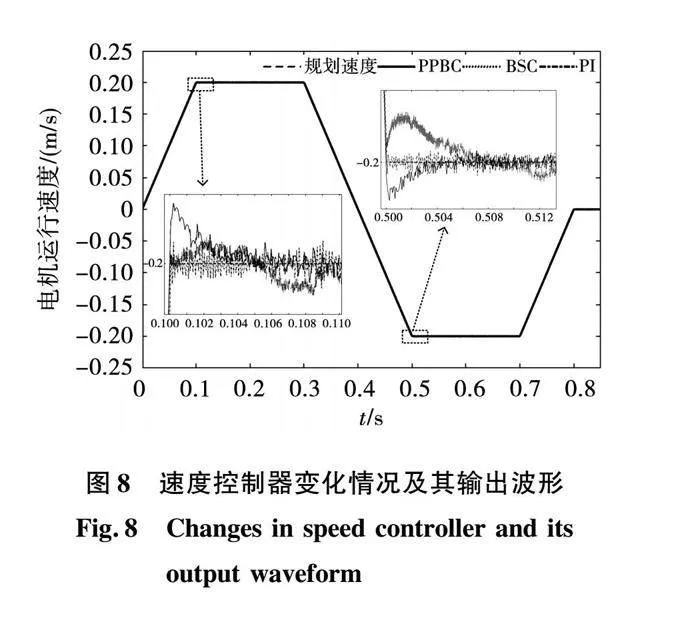
圖7、圖8、圖9分別是三種控制方法在表1軌跡1下電流環控制器的變化情況及其輸出波形，位置控制器參數的變化情況及其輸出波形、以及速度控制器參數的變化情況及其輸出波形。

圖7、圖8、圖9從速度、位移的跟隨效果上證明所提策略的可行性。圖7中i*q為電流環輸入，iq為電流反饋值。圖8表明，在加速度變化時，BSC和PPBC的波動較大，尤其是0.1 s和0.5 s前后，但是PPBC在速度突變后，相比于BSC算法可以快速調節穩定，而BSC算法穩定的時間較長；圖9給出了跟隨效果示意圖，啟動階段，相比于PI控制，PPBC和BSC有更快的響應速度和更好的跟隨效果，但是在0.8 s運動結束時，BSC有較大的誤差，PPBC總體上效果最好，滿足定位精度的要求。

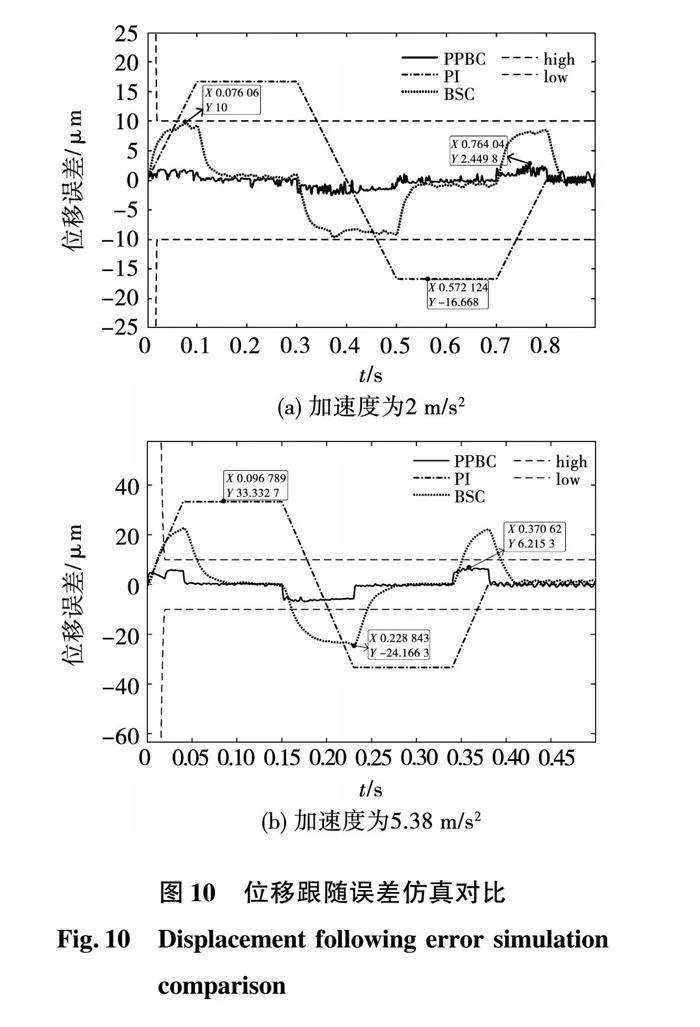
此外，由于電機跟隨效果能直觀地體現在位移誤差上，為驗證不同條件下三種策略的可行性，根據表1給出的軌跡規劃對三種策略從位移誤差的方面進一步進行仿真分析，其仿真結果如圖10所示。

圖10為不同參考軌跡下三種控制策略的位移誤差仿真對比。從圖10（a）中可以看出，在a=2 m/s2時，PPBC策略的最大位移誤差為2.45 μm；BSC策略的位移誤差曲線與加速度曲線呈明顯的正相關，最大位移誤差為10 μm；傳統二自由度PI策略最大位移誤差為16.67 μm，高于其余兩種策略的位移誤差。從圖10（b）中可以看出，在a=5.38 m/s2時，PPBC策略的最大位移誤差為6.22 μm；BSC策略最大位移誤差為24.17 μm；PI策略最大位移誤差為33.33 μm；PPBC降低位移誤差的效果遠優于BSC和PI控制，仿真驗證了在不同速度下PPBC策略在降低位移誤差方面的可行性。

3.2 實驗結果

在3.1仿真的基礎上，采用表1給出的軌跡進行不同加速度下的實驗，對比預設性能反步控制PPBC、傳統反步控制BSC以及傳統PI控制策略的位移誤差。

實驗平臺如圖11所示，其中主要包括：永磁同步直線電機、驅動器、PowerPMAC控制器以及工控機等。通過工控機對電機進行操作，Power PMAC控制器進行控制程序的編寫，同時發出指令信號給驅動器，驅動器驅動電機進行運動，電機運動的同時微米級光柵尺實時準確地把運動電機軸的位置等信號反饋給運動控制系統，繼而對與給定位移進行比較后得到的位移誤差進行約束控制。

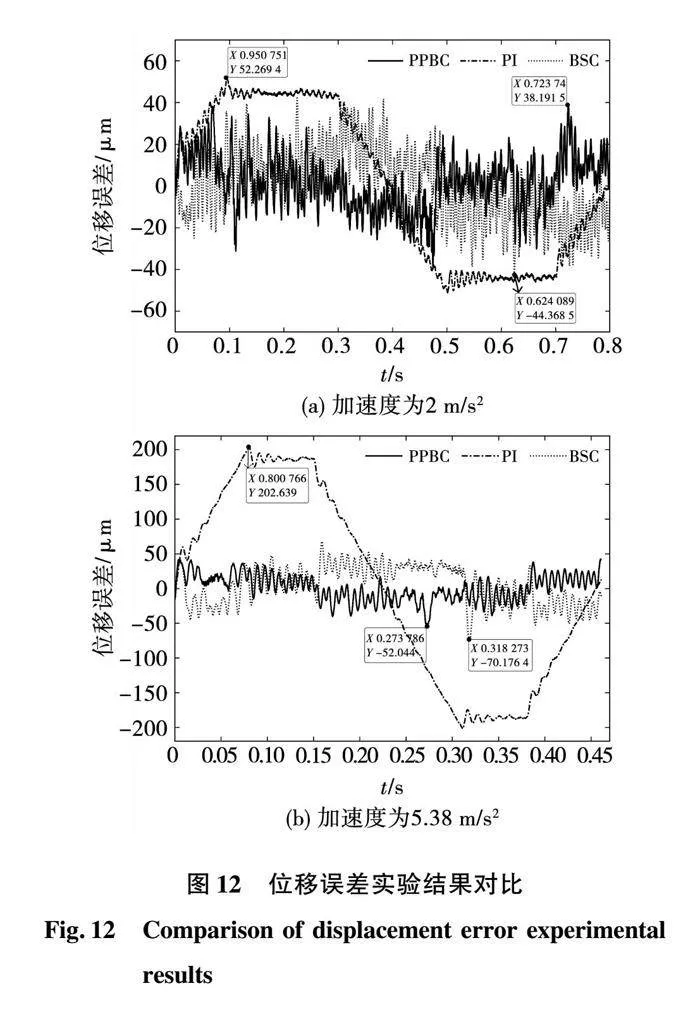
實驗參數在仿真參數的基礎上，主要以位移誤差均方根值最小和最大誤差最小為優化目標進行調整，位移誤差由實驗平臺運算后得到其均方根值。最終實驗參數為：BSC控制策略的控制參數k1=575，k2=2 850；PPBC控制策略的控制參數k1=250，k2=600。圖12給出了不同參考軌跡下3種控制策略的位移誤差實驗對比。

從圖12（a）可以看出，在a=2 m/s2時，PPBC策略的最大位移誤差為38.19 μm；BSC策略最大位移誤差為44.37 μm；傳統二自由度PI策略最大位移誤差為52.27 μm，高于其余兩種策略的位移誤差。從圖12（b）可以看出，在a=5.38 m/s2時，PPBC策略的最大位移誤差為52.04 μm；BSC策略最大位移誤差為70.18 μm；傳統二自由度PI策略最大位移誤差為202.64 μm。實驗證明，PPBC在低速運行條件下由于摩擦力的影響較大，相比于BSC策略，PPBC策略降低位移誤差的優化效果不大，但在高加速度條件下，PPBC策略降低誤差的能力有明顯提升。此外，經測量三種算法在PMAC控制器中的運算時間差異極小，傳統反步控制策略的計算時間比傳統PI控制多了27%，引入預設性能的反步策略相對于傳統反步控制的運算時間僅多了0.681%。

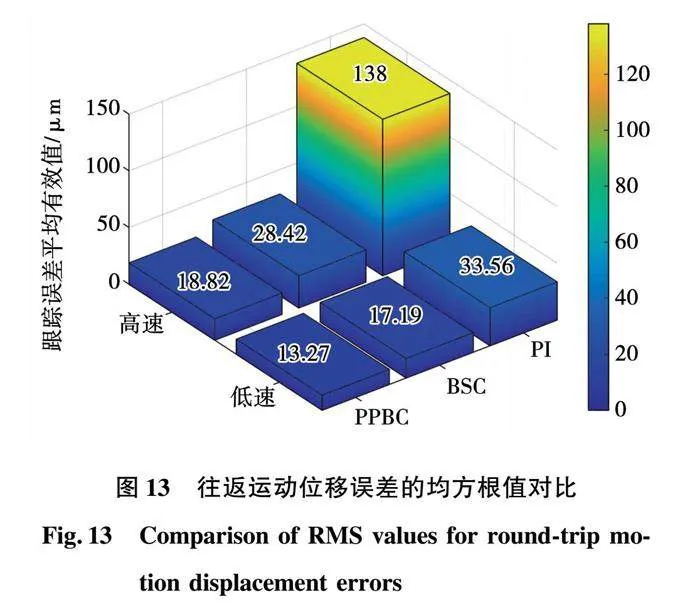
圖13是三種控制策略位移誤差的均方根值，可以直觀看出PPBC高速和低速條件下能有效降低電機的位移誤差。

從圖13可以看出，在低速條件下，PPBC的誤差均方根為13.27 μm，BSC為17.19 μm，PI為33.56 μm， PPBC相比BSC對誤差降低的效果不明顯，原因是低速條件下摩擦力對誤差的影響較大；在高速條件下，PPBC的誤差均方根為18.82 μm。BSC為28.42 μm，PI為138 μm，PPBC降低位移誤差的能力好于PI控制和BSC控制，更具有魯棒性。

4 結 論

針對非線性電機驅動控制系統位移誤差收斂不確定的問題，提出了一種具有預設性能的反步控制方法。通過引入規定的性能函數和誤差變換函數，可以定量地設計系統的暫態和穩態性能。與一般的預設性能函數相比，采用有限時間內收斂到穩態值的預設性能函數來約束直線電機的跟蹤誤差，不僅具有更快的收斂速度，還可以控制誤差收斂的時間，從而快速收斂，有效降低電機的位移誤差。

實驗結果表明，在低加速條件下，PPBC相對于BSC、PI控制來說，誤差分別降低了22.8%、60.46%；在高加速條件下，PPBC相對于BSC、PI控制來說，誤差分別降低了33.78%、86.36%；所提出的策略能有效降低永磁同步直線電機電驅系統的位移誤差，大大提高了系統的控制性能。

參 考 文 獻：

［1］ 嚴樂陽，葉佩青，張勇，等.圓筒型永磁直線同步電機用線性霍爾位置檢測的誤差補償［J］.電工技術學報， 2017， 32（5）：26.

YAN Leyang， YE Peiqing， ZHANG Yong， et al. Error compensation of linear hall based position detection for tubular permanent magnetic linear synchronous motor［J］. Transactions of China Electrotechnical Society， 2017， 32（5）： 26.

［2］ 王麗梅， 李兵. 直線電機驅動XY平臺的速度場軌跡規劃與控制研究［J］.中國電機工程學報， 2014， 34（3）： 438.

WANG Limei， LI Bing. Research on trajectory planning of contour control for a linear motor drive XY table based on velocity eld［J］. Proceedings of the CSEE， 2014， 34（3）： 438.

［3］ 林獻坤， 張薇， 樊振華. 直線電機驅動進給軸熱動態偽滯后建模與補償方法研究［J］.機械工程學報， 2018（19）：7.

LIN Xiankun， ZHANG Wei， FAN Zhenhua. Thermal dynamic hysteresis modeling and compensation for linear motor driven feed mechanism［J］.Journal of Mechanical Engineering，2018（19）：7.

［4］ TING C S， CHANG Y N， SHI B W. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive［J］. IET Electric Power Applications， 2015， 9（3）： 265.

［5］ 肖啟明， 楊明， 劉可述， 等. PMSM伺服系統速度環PI控制器參數自整定及優化［J］.電機與控制學報， 2014， 18（2）：102.

XIAO Qiming， YANG Ming， LIU Keshu， et al. Parameter self-tuning and optimization of speed PI controller for PMSM servo system［J］. Electric Machines and Control， 2014， 18（2）： 102.

［6］ 禹聰， 康爾良. 永磁同步電機模糊滑模速度控制器設計［J］.電機與控制學報， 2022， 26（7）： 98.

YU Cong， KANG Erliang. Design of fuzzy sliding mode speed controller for permanent magnet synchronous motor［J］. Electric Machines and Control， 2022，26 （7）： 98.

［7］ 方馨， 王麗梅， 張康. 基于擾動觀測器的永磁直線電機高階非奇異快速終端滑模控制［J］. 電工技術學報， 2023， 38（2）： 409.

FANG Xin， WANG Limei， ZHANG Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer［J］. Transactions of China Electrotechnical Society， 2023， 38（2）： 409.

［8［ 曹陽， 郭健. 基于特征模型的永磁同步直線電機自適應控制［J］. 電機與控制學報， 2024， 28（3）： 131.

CAO Yang， GUO Jian.Adaptive control of permanent magnet synchronous linear motor based on characteristic model［J］. Electric Machines and Control， 2024， 28（3）： 131.

［9］ XU L，YAO B.Adaptive robust precision motion control of linear motors with negligible electrical dynamics： theory and experiments［J］.IEEE/ASME Transactions on Mechatronics，2001，6（4）：444.

［10］ 嚴樂陽， 葉佩青， 張輝， 等. 基于多周期迭代滑模控制的直線電機干擾抑制［J］. 電機與控制學報， 2017， 21（1）： 8．

YAN Yueyang， YE Peiqing， ZHANG Hui， et al. Disturbance rejection for linear motor based on multi-periodic learning variable structure control［J］. Electric Machines and Control， 2017， 21（1）：8.

［11］ 曹榮敏， 鄭鑫鑫， 侯忠生. 基于改進多入多出無模型自適應控制的二維直線電機迭代學習控制［J］.電工技術學報， 2021，36（19）：4025.

CAO Rongmin， ZHENG Xinxin， HOU Zhongsheng. An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-dimensional linear motor［J］. Transactions of China Electrotechnical Society， 2021， 36（19）： 4025.

［12］ KANELLAKOPOULOS I， KOKOTOVIC P V， MORSEA S. Systematic design of adaptive controllers for feedback linearizable systems［J］. IEEE Transactions on Automatic Control， 1991， 36（11）： 1241.

［13］ KANELLAKOPOULOS I， KREIN P T， DISILVESTROF. Nonlinear ux-observer-based control of induction motors［C］// 1992 American Control Conference， June 24-26，1992，Chicago，USA. 1992： 1700-1705.

［14］ 張慶超， 馬瑞卿. 無刷直流電機轉速伺服系統反步高階滑模控制［J］. 控制與決策， 2016， 31（6）： 961.

ZHANG Qingchao， MA Ruiqing. Backstepping high order sliding mode control for brushless DC motor speed servo control system［J］. Control and Decision， 2016， 31（6）： 961.

［15］ HAMIDA M A， GLUMINEAU A， LEON J D. Robust integral backstepping control for sensorless IPM synchronous motor controller［J］. Journal of the Franklin Institute， 2012， 349（5）： 1734.

［16］ 紀志成， 李三東， 沈艷霞. 自適應積分反步法永磁同步電機伺服控制器的設計［J］. 控制與決策， 2005， 20（3）： 329.

JI Zhicheng， LI Sandong， SHEN Yanxia. Adaptive backstepping design for the servo controller of permanent magnet synchronous motor［J］. Control and Decision， 2005， 20（3）： 329.

［17］ 張康， 王麗梅. 基于周期性擾動學習的永磁直線電機自適應滑模位置控制［J］.電機與控制學報， 2021，25（8）： 132.

ZHANG Kang， WANG Limei. Adaptive sliding mode position control for permanent magnet linear motor based on periodic disturbance learning ［J］. Electric Machines and Control， 2021， 25（8）： 132.

［18］ BECHLIOULIS P C， ROVTHAKIS G A. Robust adaptive control of feedback lineaizable MIMO nonlinear systems with prescribed performance［J］. IEEE Transactions on Automatic Control， 2008， 53 （9）： 2090.

［19］ BECHLIOULIS P C， GEORGE A R. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedbacksystems［J］. Automatica， 2009， 45（2）： 532.

［20］ 王琦， 陳龍勝. 非仿射純反饋不確定系統預設性能魯棒自適應控制［J］. 電機與控制學報， 2017， 21（2）： 109.

WANG Qi， CHEN Longsheng. Prescribed performance adaptive robust control for a class of uncertain non-affine pure feedback system［J］. Electric Machines and Control， 2017， 21（2）： 109．

［21］ CHENG W， ZHANG K， JIANG B， et al. Fixed-time fault-tolerant formation control for heterogeneous multi-agent systems with parameter uncertainties and disturbances［J］. IEEE Transactions on Circuits and Systems I： Regular Papers， 2021： 1.

［22］ 王鵬飛， 王潔， 時建明， 等. 高超聲速飛行器預設性能反演魯棒控制［J］. 電機與控制學報， 2017， 21（2）： 94.

WANG Pengfei， WANG Jie， SHI Jianming， et al. Prescribed performance back-stepping robustness control of a exible hypersonic vehicle［J］. Electric Machines and Control， 2017， 21（2）： 94.

［23］ HUANG Y， NA J， WU X， et al. Adaptive control of nonlinear uncertain active suspension systems with prescribed performance［J］. ISA Transactions， 2015， 54（1）： 145 .

［24］ NA J， CHEN Q， REN X， et al. Adaptive prescribed performance motion control of servo mechanisms with friction compensation［J］. IEEE Transactions on Industrial Electronics， 2014， 61（1）： 486 .

［25］ 陳子印， 林喆， 賈鶴鳴， 等. 永磁同步電機有限時間預設性能控制［J］. 控制理論與應用， 2021， 38（4）： 479.

CHEN Ziyin， LIN Zhe， JIA Heming， et al. Finite-time control for permanent magnet synchronous motor with prescribed performance［J］. Control Theory amp; Applications， 2021， 38（4）： 479.

（編輯：劉素菊）