變式彰顯本質　探究深化思維

課本習題是我們鞏固數學知識、形成思維方法、提升解題技能的有效陣地. 解決課本習題之后，若能大膽變化問題的相關條件，或通過變換問題的情境向縱深進行拓展和延伸，挖掘蘊含的數學思想方法，再次經歷問題變化過程的探索與思考，可增強我們解決問題的能力.

引例 （人教版九年級數學第25頁“綜合應用”部分第8題）如下頁圖（略），利用一面墻（墻的長度不限），用20 m長的籬笆，怎樣圍成一個面積為50 m2的矩形場地？

解答過程略.

反思：本題中給出的墻面的長度沒有限制，因此對求出的答案沒有影響，只要答案符合實際意義（正實數）即可. 若給出的墻面的長度有限制，必然制約著問題的答案（這是因為墻面短時，就不能圍成所需場地）.

變式1：將墻的長度不限變為墻的長度有限制，并在原來圍成的矩形與墻平行的一邊上預留入口（不用籬笆圍），探究矩形的邊長或矩形面積問題.

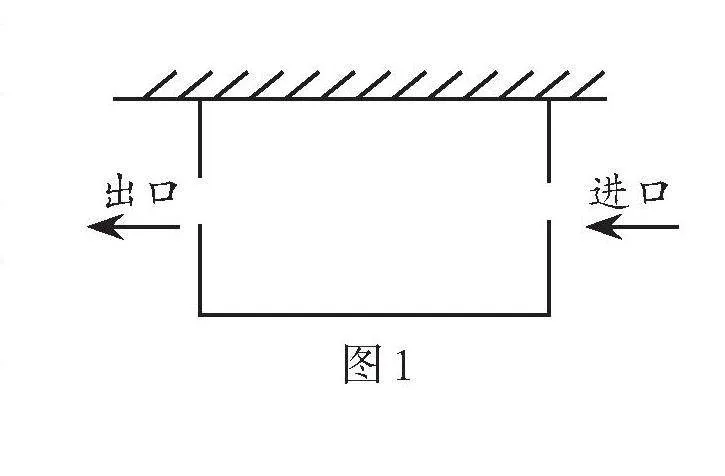
例1 某小區居委會為了居民生活安全，方便居民的電瓶車充電，準備利用一邊靠墻（墻長15 m）的空曠場地用柵欄圍成一個面積為80 m2的電瓶車充電區. 如圖1，為了方便進出，在兩邊空出兩個寬各為2.5 m的出入口，一共用去柵欄21 m. 請問長方形充電區的相鄰兩邊長分別是多少米.

解析：設這個長方形充電區垂直于墻的一邊是[x] m，

則平行于墻的一邊為（[21+2.5+2.5-2x]） m，即（[26-2x]） m.

根據充電區的面積為80 m2，可得[x]（[26-2x]） [=80]，

解得[x1=5]，[x2=8].

當[x=5]時，[26-2x=16>15]，

此時墻不夠長，無法構成封閉區域，不合題意，故舍去.

當[x=8]時，[26-2x=10].

答：長方形充電區的相鄰兩邊長分別是8 m和10 m.

點評：在垂直于墻的一邊上留有兩個2.5 m寬的進出口，相當于柵欄材料增加了5 m. 正確用垂直于墻的一邊長[x]表示出與墻平行的邊長的代數式是解決本題的關鍵，也是本題易錯的地方. 根據墻長對一元二次方程的解進行取舍是另一個易錯點.

變式2：將墻的長度不限變為墻的長度有限制，并在原來的矩形場地內加入若干道籬笆，探究矩形的邊長.

例2 如圖2，有一道長為25 m的墻，計劃用總長為50 m的柵欄，靠墻圍成由三個小長方形組成的矩形花圃[ABCD]. 若花圃[ABCD]的面積為150 m2，求[AB]的長.

解析：設[AB=x] m，則[BC=50-4xm].

根據花圃[ABCD]的面積為[150 m2]，

可得方程[x50-4x=150]，

化簡，整理得[2x2-25x+75=0]，

解得[x1=5]，[x2=152].

當[x=5]時，[50-4x=50-4×5=30>25]，不合題意，舍去；

當[x=152]時，[50-4x=50-4×152=20<25]，符合題意.

故[AB]的長為[152m].

點評：問題的相等關系仍然是矩形的面積公式，但本題由于給出墻的長度為25 m，因此對一元二次方程的解起到限制作用，這也是同學們必須注意的地方.

變式3：墻長無限制條件，但在原來的矩形場地內加入若干道籬笆且在圍成的矩形的邊上開兩扇門，探究矩形的邊長或符合一定面積的矩形是否存在.

例3 如圖3，利用足夠長的一段圍墻，用籬笆圍一個長方形的場地，中間用籬笆分割出2個小長方形，與墻平行的一邊上各開一扇寬為1 m的門，總共用去籬笆34 m.

（1）為了使這個長方形[ABCD]的面積為96 m2，求邊[AB]為多少米.

（2）用這些籬笆，能使圍成的長方形[ABCD]面積是110 m2嗎？說明理由.

[A][B][D][C][E][F]

圖3

解析：（1）設[AB]的長為[x] m，則BC = （[34+2-3x]） [m]，

由矩形的面積公式，可得方程[x]（[34+2-3x]） [=96]，

解得[x1=4]，[x2=8].

故當[AB]的長度為4 m或8 m時，長方形[ABCD]的面積為96 m2.

（2）不能.

理由：假設長方形[ABCD]的面積是110 m2，

依題意得[x]（[34+2-3x]） [=110]，即[3x2-36x+110=0].

[∵]Δ [=-362-4×3×110=-24<0]，

[∴]該一元二次方程無實數根，

[∴]假設不成立.

故用這些籬笆不能圍成面積為110 m2的長方形.

點評：在墻長沒有限制的條件下，只要方程有正實數解，就滿足條件；對于（2）問，可以先假設滿足條件的矩形存在，然后根據面積列出關于邊長的一元二次方程，探究方程有無實數解，進一步判斷假設是否成立，從而獲得問題的答案.

變式4：改變問題的情境，將墻的形狀改變為直角墻角，探究特定點是否在矩形內.

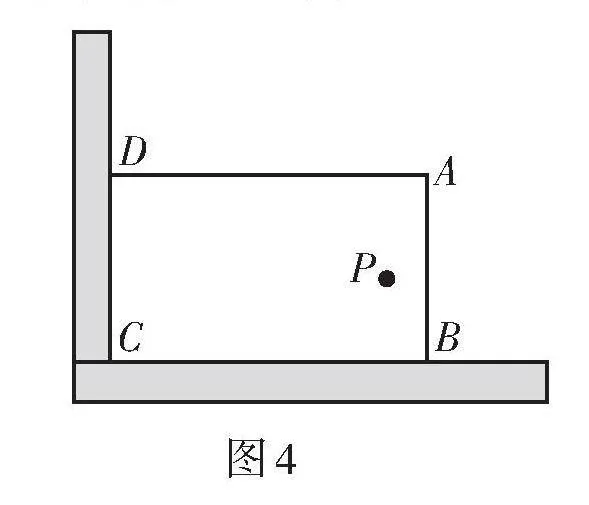
例4 某社區在開展“美化社區，幸福家園”活動中，計劃利用如圖4所示的直角墻角（陰影部分，兩邊足夠長），用40 m長的籬笆圍成一個矩形花園[ABCD]（籬笆只圍[AB]，[AD]兩邊），設[AB=x] m2.

（1）若花園的面積為300 m2，求[x]的值；

（2）若在直角墻角內點[P]處有一棵桂花樹，且與墻[BC]，[CD]的距離分別是10 m、24 m，要將這棵樹圍在矩形花園內（含邊界，不考慮樹的粗細），則花園的面積能否為400 m2？若能，求出[x]的值；若不能，請說明理由.

[P][D][A][B][C]

圖4

解析：（1）[∵AB=x] m，[∴BC=40-x] m，

由題意得[x40-x=300]，

解得[x1=10]，[x2=30]，

即[x]的值為10或30.

（2）花園的面積不能為400 m2，理由如下：

由題意得[x40-x=400]，

解得[x1=x2=20].

當[x=20]時，[40-x=40-20=20]，

即當[AB=20] m時，[BC=20] m [<24] m，這棵樹沒有被圍在花園內，

[∴]要將這棵樹圍在矩形花園內（含邊界，不考慮樹的粗細），則花園的面積不能為400 m2.

點評：解決本題的關鍵仍然是利用矩形的面積作為相等關系構造一元二次方程，只是需要根據是否符合實際問題的要求對解進行取舍.

拓展訓練

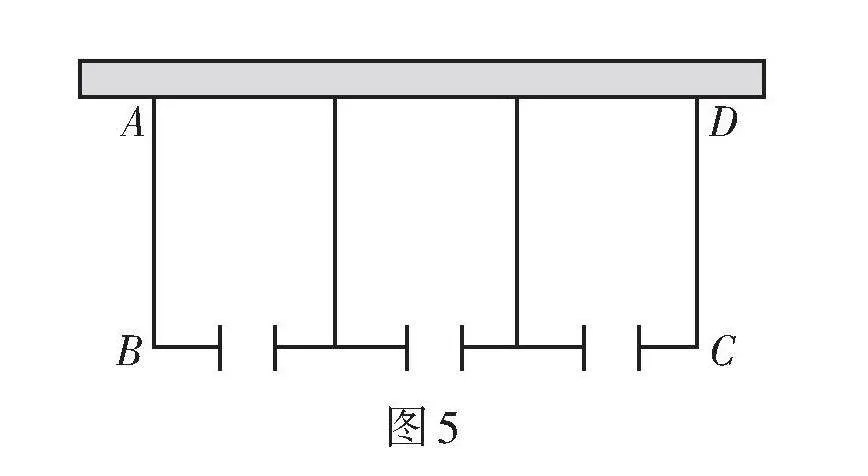
1. 如圖5，用一段77 m的籬笆圍成三個一邊靠墻、大小相同的長方形羊圈，每個長方形都有一個1 m的門，墻的最大可用長度為30 m.

（1）如果羊圈的總面積為300 m2，求邊[AB]的長.

（2）請問羊圈的總面積能為440 m2嗎？若能，請求出邊[AB]的長；若不能，請說明理由.

[A][D][C][B]

圖5

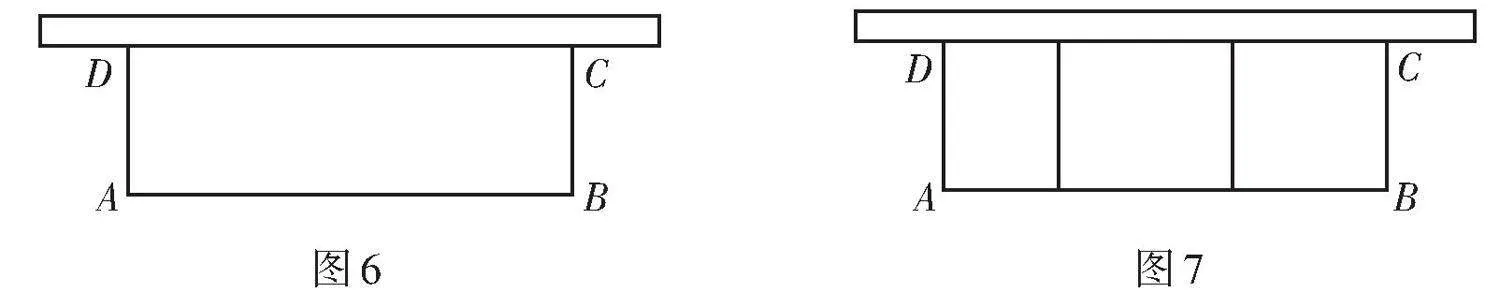
2. 2022年9月，教育部正式印發《義務教育課程方案》，勞動教育成為一門獨立的課程，某學校率先行動，在校園開辟了一塊勞動教育基地：一面利用學校的墻（墻的最大可用長度為15 m），用長為30 m的籬笆，圍成矩形養殖園，如圖6. 已知矩形的邊[CD]靠院墻，[AD]和[BC]與院墻垂直，設[AB]的長為[x] [m].

[D][A][B][C] [D][A][B][C]

圖6 圖7

（1）當圍成的矩形養殖園面積為[100 m2]時，求[BC]的長.

（2）如圖7，該學校打算在養殖園飼養雞、鴨、鵝三種家禽，需要在中間多加上兩道籬笆作為隔離網，并與院墻垂直，請問此時養殖園的面積能否達到[100 m2]？若能，求出[AB]的長；若不能，請說明理由.

答案：1. （1）邊[AB]的長為15 m；

（2）羊圈的總面積不能為440 m2.

2. （1）[BC]的長為[10 m]；

（2）不能，理由略.

（作者單位：江蘇省鹽城市先鋒實驗學校）