基于RBF神經(jīng)網(wǎng)絡(luò)的建筑暖通水溫節(jié)能控制設(shè)計


摘 要:本文基于RBF神經(jīng)網(wǎng)絡(luò)提出一種超低能耗建筑暖通空調(diào)冷水溫度優(yōu)化控制方法。在該方法中,對建筑暖通空調(diào)水系統(tǒng)的運(yùn)行工況進(jìn)行辨識。通過辨識結(jié)果,建立建筑暖通空調(diào)冷水溫度優(yōu)化控制器,利用RBF 神經(jīng)網(wǎng)絡(luò)對控制器進(jìn)行在線優(yōu)化,獲取房間預(yù)測溫度輸出。利用預(yù)測信息和設(shè)定的目標(biāo)函數(shù),不斷在線修正預(yù)測溫度輸出,得到最佳暖通空調(diào)冷水溫度,對空調(diào)冷水溫度進(jìn)行優(yōu)化控制。試驗結(jié)果表明,該方法能夠有效地對建筑暖通水溫進(jìn)行節(jié)能控制,具有較高的控制精度和可靠性。
關(guān)鍵詞:RBF神經(jīng)網(wǎng)絡(luò);建筑暖通;水溫節(jié)能控制
中圖分類號:TU 83" " 文獻(xiàn)標(biāo)志碼:A
隨著人們對能源消耗和環(huán)境保護(hù)的日益關(guān)注,建筑節(jié)能成為一個重要的研究領(lǐng)域[1]。建筑暖通系統(tǒng)是建筑能耗的重要組成部分,其中水溫控制是影響能耗和舒適性的關(guān)鍵因素之一。傳統(tǒng)的建筑暖通水溫控制方法往往存在能耗高、控制精度低等問題。張帆等[3]采用蟻群算法來增強(qiáng)其全局搜索能力。葉立等[2]則引入粒子群優(yōu)化算法來對控制器參數(shù)進(jìn)行優(yōu)化。本文以此為基礎(chǔ),基于RBF神經(jīng)網(wǎng)絡(luò)進(jìn)行建筑暖通水溫節(jié)能控制設(shè)計。
1 建筑暖通水溫節(jié)能優(yōu)化控制方法
1.1 建筑暖通空調(diào)水系統(tǒng)運(yùn)行工況分析
在神經(jīng)網(wǎng)絡(luò)中,使用公式(1)來描述神經(jīng)元的計算過程。
xi=∑(ωi×xi-1)+θ " "(1)
式中:xi為第i個神經(jīng)元的輸入;ωi為神經(jīng)元之間的連接強(qiáng)度;xi-1為第i-1個神經(jīng)元的輸出;θ為閾值。
計算神經(jīng)元的激活函數(shù)如公式(2)所示。
(2)
式中:f()為激活函數(shù);exp()為指數(shù)函數(shù)。
神經(jīng)元的輸入是由前一層神經(jīng)元的輸出和連接強(qiáng)度加權(quán)求和得到的,再加上閾值,通過激活函數(shù)對輸入進(jìn)行非線性轉(zhuǎn)換,得到神經(jīng)元的輸出。
計算隱含層的輸出如公式(3)所示。
bf=f ∑((ωij×bf-1)+θj ) (3)
計算輸出層的輸出如公式(4)所示。
cf=f ∑((υij×bf-1)+γj) (4)
式中:bj為隱含層的輸出;cf為輸出層的輸出;ωij為神經(jīng)元i和j之間的連接強(qiáng)度;υij為神經(jīng)元i和j之間的權(quán)值系數(shù);θj為神經(jīng)元的連接強(qiáng)度閾值;γj為神經(jīng)元i的閾值;f()為激活函數(shù)。
計算輸出層的一般化誤差如公式(5)所示。
ekj=Ct-tk " "(5)
式中:ekj為輸出層的一般化誤差;Ct為輸出層的輸出;tk為目標(biāo)值。
計算誤差函數(shù)的極小值如公式(6)所示。
ykt=∑(ekj2)" (6)
式中:ykt為誤差函數(shù)的極小值;ekj為輸出層的一般化誤差。
計算輸出層的誤差,并根據(jù)誤差函數(shù)的極小值來評估神經(jīng)網(wǎng)絡(luò)的性能。輸出層的一般化誤差是輸出層輸出與目標(biāo)值之間的差異,即網(wǎng)絡(luò)的預(yù)測誤差。誤差函數(shù)的極小值是對所有輸出層神經(jīng)元的一般化誤差進(jìn)行求和。在訓(xùn)練過程中,通過調(diào)整神經(jīng)網(wǎng)絡(luò)的參數(shù)和權(quán)重來最小化誤差函數(shù)的極小值,從而提高網(wǎng)絡(luò)的預(yù)測準(zhǔn)確性。常用的方法是使用梯度下降算法來更新參數(shù)和權(quán)重,以逐步減小誤差函數(shù)的極小值[4-5]。
圖1為遺傳算法的流程圖,第一步是將種群進(jìn)行初始化處理。在實際編碼的過程中,通常使用實數(shù)進(jìn)行編碼,以便更靈活地表示網(wǎng)絡(luò)的結(jié)構(gòu)和權(quán)值。
在遺傳算法的每一代中,需要計算不同個體的適應(yīng)度,適應(yīng)度函數(shù)通常為評估個體解決問題能力的指標(biāo)。具體適應(yīng)度函數(shù)的選擇取決于具體的問題和目標(biāo)。根據(jù)適應(yīng)度函數(shù)的計算結(jié)果,可以對種群中的個體進(jìn)行排序,以便選擇適應(yīng)度較高的個體作為下一代的父代,從而保留優(yōu)秀的個體解。
在遺傳算法中,根據(jù)個體的適應(yīng)度值和概率,可以選擇不同的網(wǎng)絡(luò)個體作為下一代的父代。具體的選擇如公式(7)所示。
(7)
式中:pi為個體i被選中的概率,fi為個體i的適應(yīng)度值。通過將個體的適應(yīng)度值歸一化,可以得到每個個體被選中的概率。
根據(jù)這些概率值,可以使用輪盤賭選擇(Roulette Wheel Selection)的方法。該方法的基本思想是根據(jù)個體被選中的概率,在輪盤上選擇父代個體。
計算累積概率:qi=∑pi,即第i個個體被選中的累積概率。生成一個隨機(jī)數(shù)r,使0≤r≤1。
根據(jù)隨機(jī)數(shù)r,選擇第一個滿足qi-1≤r≤qi的個體作為父代。
通過這樣的選擇過程,可以根據(jù)個體的適應(yīng)度值選擇適應(yīng)度較高的個體作為下一代的父代,進(jìn)一步進(jìn)行遺傳操作,從而優(yōu)化網(wǎng)絡(luò)的結(jié)構(gòu)和權(quán)值。
首先,根據(jù)概率pc,選擇進(jìn)行交叉操作的個體,通常是選擇適應(yīng)度較高的個體。其次,從選中的個體中隨機(jī)選擇兩個個體作為父代,進(jìn)行交叉操作,可以采用不同的交叉方式,例如單點交叉、多點交叉等。交叉操作會交換兩個個體的染色體片段,生成兩個新的個體。最后,重復(fù)上述步驟,以保留優(yōu)秀的個體。
通過概率pm突變形成全新的個體。突變操作是為了引入新的基因變異,以增加種群的多樣性。根據(jù)概率pm,選擇進(jìn)行突變操作的個體,一般是選擇適應(yīng)度較低的個體。對選中的個體進(jìn)行基因突變操作,即隨機(jī)改變個體的某些基因值。重復(fù)上述步驟,直到所有選中的個體都進(jìn)行了突變操作。
將獲取的全新個體直接放置到種群P中,計算對應(yīng)的評價函數(shù)。將經(jīng)過交叉和突變操作得到的全新個體放置到原始種群P中,形成下一代種群。計算新種群中的個體的評價函數(shù)。可以根據(jù)具體問題的需求來定義評價函數(shù),一般是根據(jù)個體解決問題的能力來評估其適應(yīng)度值。
在遺傳算法中,根據(jù)ANN的誤差平方和來判斷是否達(dá)到設(shè)定值。如果誤差平方和已經(jīng)滿足設(shè)定值,那么算法結(jié)束,進(jìn)行下一步驟。
將GA的初始優(yōu)化值設(shè)定為權(quán)值,借助BP神經(jīng)網(wǎng)絡(luò)對其進(jìn)行訓(xùn)練,直至滿足系統(tǒng)設(shè)定的精度條件。
在暖通空調(diào)系統(tǒng)中,水泵是將冷卻水或熱水輸送到機(jī)組或冷熱源的關(guān)鍵設(shè)備。水泵的效率直接影響到系統(tǒng)的能耗和運(yùn)行費(fèi)用。較高的水泵效率可以減少能源消耗,降低能耗成本。可以通過其工作點的位置來評估水泵的效率。工作點是指水泵在一定流量和揚(yáng)程下的運(yùn)行狀態(tài)。水泵的效率隨著工作點的改變而變化,通常在其最高效率點附近工作過程中能夠?qū)崿F(xiàn)最佳效率。
對比不同矛盾結(jié)果對空調(diào)水系統(tǒng)的影響,如公式(8)所示。
(8)
式中:COPS為每單位的制冷負(fù)荷所需的能耗;Q為數(shù)據(jù)組的預(yù)測值,表示冷水機(jī)組的制冷負(fù)荷;W1為電機(jī)的輸入功率,表示冷水機(jī)組電機(jī)的能耗;W2為泵的輸入功率,表示冷水機(jī)組水泵的能耗。COPS值越小,表示冷水機(jī)組的能效越高,能夠以較少的能耗達(dá)到相同的制冷效果。
1.2 超低能耗建筑暖通空調(diào)冷水溫度優(yōu)化控制
PMV指標(biāo)表示相同室內(nèi)環(huán)境下大部分人的熱舒適度。這個指標(biāo)考慮了人體的熱代謝和熱輻射等因素以及環(huán)境溫度、相對濕度、氣流速度等因素對人體熱舒適度的影響。由于每個人體質(zhì)和敏感度不同,有些人可能對相同的熱環(huán)境感到不舒適。因此,需要利用PPD指標(biāo)來表示用戶對熱環(huán)境不滿意的百分比。PPD指標(biāo)反映了人體對室內(nèi)熱環(huán)境的敏感度,即有多少人在相同環(huán)境下感到不舒適。由于PMV指標(biāo)更加重視用戶對熱舒適度的滿意度,因此在房間溫度的設(shè)定方面,需要更多地考慮PMV指標(biāo)。同時,還需要考慮其他影響因素,例如相對濕度和空氣流動速度等。
輸入節(jié)點數(shù)量為6個,包括環(huán)境溫度、相對濕度、氣流速度等因素。可以根據(jù)實際情況調(diào)整隱層節(jié)點數(shù)量,以得到最佳的預(yù)測結(jié)果。輸出節(jié)點可以是PMV或者PPD指標(biāo),以便于對室內(nèi)環(huán)境進(jìn)行優(yōu)化和調(diào)整。
計算超低能耗建筑暖通空調(diào)冷水調(diào)節(jié)電壓,如公式(9)所示。
u(k+N)=∑(i=1toM)(ω(i)×ρi) (9)
式中:u(k+N)為在時間步k+N時刻的冷水調(diào)節(jié)電壓;M為模糊神經(jīng)網(wǎng)絡(luò)的輸出節(jié)點數(shù)量;ω(i)為每個節(jié)點的權(quán)重;ρi為空調(diào)調(diào)節(jié)閥電壓取值。
在模糊神經(jīng)網(wǎng)絡(luò)中,通過網(wǎng)絡(luò)的訓(xùn)練過程得到權(quán)重 ω(i),可以根據(jù)具體的算法和數(shù)據(jù)進(jìn)行計算和調(diào)整。這些權(quán)重可以對輸入變量與輸出變量之間的關(guān)系進(jìn)行建模和表示。通過調(diào)整權(quán)重,模糊神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)并預(yù)測未來的冷水調(diào)節(jié)電壓。
計算設(shè)定控制目標(biāo)函數(shù)j如公式(10)所示。
j=∑(i=ltoN)(ω1×|y(k+i)-λ(k+i)|ω2×yr(k+i)) " (10)
式中:N為預(yù)測時間步數(shù);ω1和ω2是權(quán)重系數(shù);|y(k+i)-λ(k+i)|為測試房間的期望溫度與實際溫度之間的差值;yr(k+i)為房間最高溫度和最低溫度的差值。
控制目標(biāo)函數(shù)的主要作用是優(yōu)化控制策略,使測試房間的期望溫度與實際溫度之間的差值最小,并且將房間的溫度控制在最高溫度和最低溫度的差值范圍內(nèi)。通過調(diào)整權(quán)重系數(shù),可以根據(jù)實際需求來平衡不同的目標(biāo)。
采用優(yōu)化方法對性能進(jìn)行優(yōu)化,可以使用RBF(徑向基函數(shù))模糊神經(jīng)網(wǎng)絡(luò)來獲取未來控制時長內(nèi)暖通空調(diào)系統(tǒng)中冷凍水泵的調(diào)節(jié)電壓,如公式(11)所示。
ρj,N(k+1)=∑(i=1tom)(ω(i)×Φ(||[aj,N(k+1),cj,N(k+1)]-[μi,σi]||)) (11)
式中:ρj,N(k+1)為經(jīng)過調(diào)整和修正后的控制參數(shù);aj,N(k+1)、cj,N(k+1)為經(jīng)過調(diào)整和修正后的控制參數(shù);ω(i)為每個節(jié)點的權(quán)重;Φ()為徑向基函數(shù);[μi,σi]為徑向基函數(shù)的中心和標(biāo)準(zhǔn)差。RBF模糊神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程通常包括確定徑向基函數(shù)的中心和標(biāo)準(zhǔn)差以及節(jié)點的權(quán)重。通過訓(xùn)練過程,模糊神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)并預(yù)測未來控制時長內(nèi)的冷凍水泵調(diào)節(jié)電壓,以優(yōu)化性能。
2 仿真研究
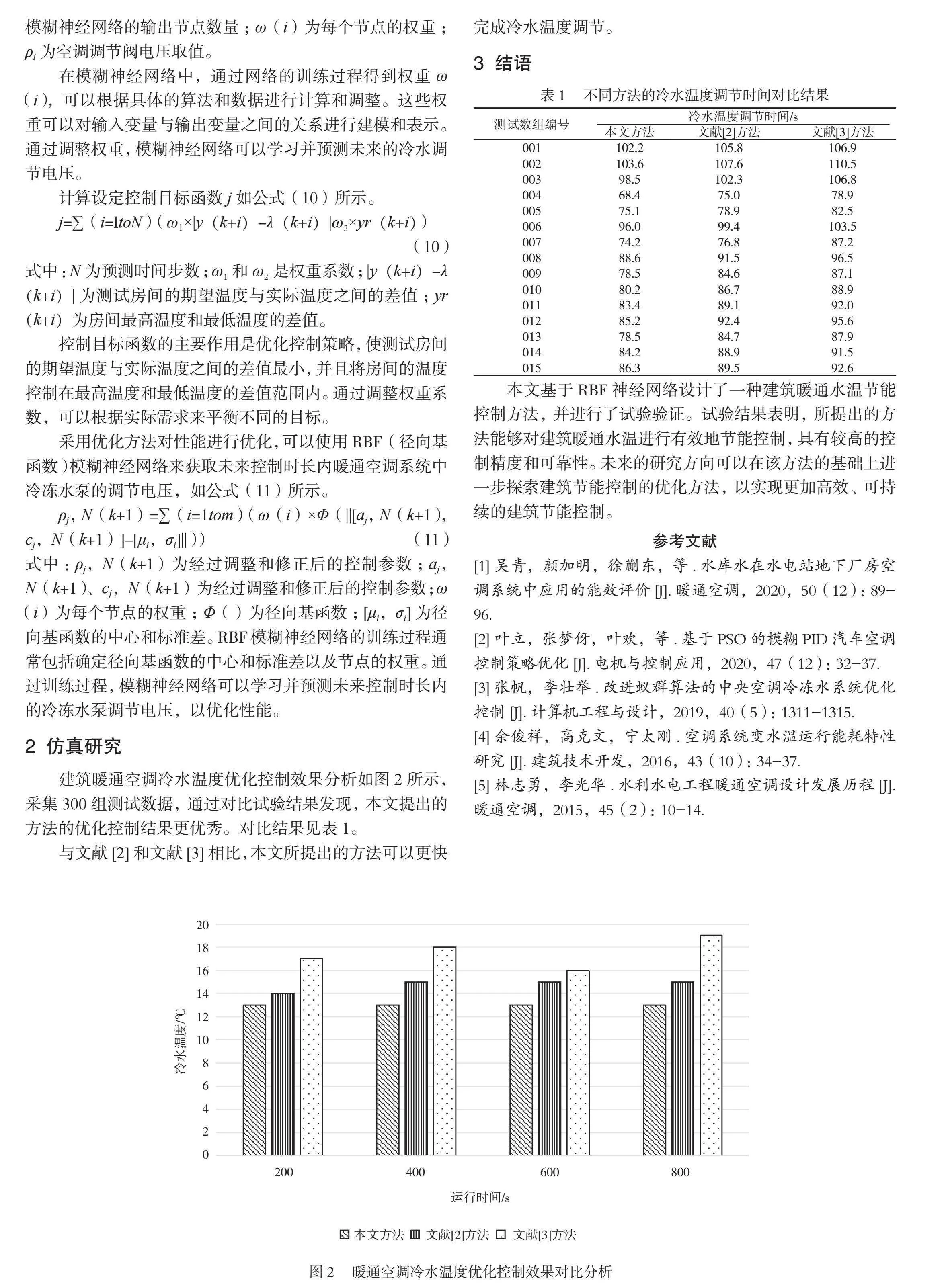
建筑暖通空調(diào)冷水溫度優(yōu)化控制效果分析如圖2所示,采集300組測試數(shù)據(jù),通過對比試驗結(jié)果發(fā)現(xiàn),本文提出的方法的優(yōu)化控制結(jié)果更優(yōu)秀。對比結(jié)果見表1。
與文獻(xiàn)[2]和文獻(xiàn)[3]相比,本文所提出的方法可以更快完成冷水溫度調(diào)節(jié)。
3 結(jié)語
本文基于RBF神經(jīng)網(wǎng)絡(luò)設(shè)計了一種建筑暖通水溫節(jié)能控制方法,并進(jìn)行了試驗驗證。試驗結(jié)果表明,所提出的方法能夠?qū)ㄖㄋ疁剡M(jìn)行有效地節(jié)能控制,具有較高的控制精度和可靠性。未來的研究方向可以在該方法的基礎(chǔ)上進(jìn)一步探索建筑節(jié)能控制的優(yōu)化方法,以實現(xiàn)更加高效、可持續(xù)的建筑節(jié)能控制。
參考文獻(xiàn)
[1]吳青,顏加明,徐蒯東,等.水庫水在水電站地下廠房空調(diào)系統(tǒng)中應(yīng)用的能效評價[J].暖通空調(diào),2020,50(12):89-96.
[2]葉立,張夢伢,葉歡,等.基于PSO的模糊PID汽車空調(diào)控制策略優(yōu)化[J].電機(jī)與控制應(yīng)用,2020,47(12):32-37.
[3]張帆,李壯舉.改進(jìn)蟻群算法的中央空調(diào)冷凍水系統(tǒng)優(yōu)化控制[J].計算機(jī)工程與設(shè)計,2019,40(5):1311-1315.
[4]余俊祥,高克文,寧太剛.空調(diào)系統(tǒng)變水溫運(yùn)行能耗特性研究[J].建筑技術(shù)開發(fā),2016,43(10):34-37.
[5]林志勇,李光華.水利水電工程暖通空調(diào)設(shè)計發(fā)展歷程[J].暖通空調(diào),2015,45(2):10-14.

