基于R語言的主成分分析與聚類分析在成績評價中的應用

摘 要：主成分分析與聚類分析是當前大數據時代較有應用前景的數據分析方法。首先介紹主成分分析與聚類分析的原理以及在R語言中的算法實現。利用主成分分析，建立一種可以綜合評價成績的方式，通過成績綜合評價的得分進行相應的排名，然后根據主成分中的得分進行聚類分析。通過對20名學生考試成績的分析與評價，得出的結果可以用來反映學生的學習情況與教師的教學成效，為成績的管理提供一種合理且便于操作的方式。

關鍵詞：主成分分析 聚類分析 K-means聚類 R語言 成績分析

中圖分類號：G642

Application of Principal Component Analysis and Cluster Analysis Based on R Language in Score Evaluation

SHEN Dandan

Changzhi Medical College， Changzhi， Shanxi Province， 046000 China

Abstract： Principal Component Analysis and Cluster Analysis are the most promising data analysis methods in the current era of big data. Firstly， it introduces the principles of Principal Component Analysis and Cluster Analysis， as well as their algorithm implementation in R language. Using Principal Component Analysis， it establishes a comprehensive score evaluation method， and ranks based on the comprehensive score evaluation， and then conducts Cluster Analysis based on the scores in the principal components. By analyzing and evaluating the exam scores of 20 students， the results can be used to reflect the learning situation of students and the teaching effectiveness of teachers， providing a reasonable and easy to operate way for score management.

Key Words： Principal Component Analysis; Cluster Analysis; K-means cluster; R language; Score analysis

當前信息化時代背景下，面對高校教學中學生成績錯綜復雜的情形，利用傳統的成績評定方式有一定的局限性，通常是采用加權評分法或對所有成績求和，然后依據絕對分數來進行等級評定。然而在設置加權的權重時，人為主觀因素較大，直接對所有成績求和無法反映學生真實的學習情況與能力，利用絕對分數來進行成績評定時很大程度上依賴于考試的形式、試卷的結構以及難易程度等，這些方法都存在一定的缺陷，不利于客觀、科學地評價學生的學習情況，也不利于真實地反映教師的教學成果。主成分分析是把所有變量之間相關聯的復雜關系進行簡化分析，聚類分析能從大量的數據中對有意義的數據分布模式進行挖掘，將主成分分析與聚類分析應用于學生成績評價時，可以彌補傳統成績評定方法所帶來的缺陷，更能科學客觀地反映學生的學習情況，從而為教學管理提供一定指導[3]。

1 主成分分析

1.1?; 主成分分析基本思想

通常研究人員所要處理的問題大多是關于多變量的問題，變量越多，反應問題的信息更全面，但也無疑給問題增加了難度，從而研究人員希望在保證不丟失大量原始信息量的基礎上，通過少量變量來反映問題。主成分分析就是采用降維的方式將具有一定相關性的多變量化為少數幾個不相關的綜合變量的統計分析方法。

主成分分析的基本原理：將原始具有相關性的變量通過線性組合的方式形成新的線性無關的變量。第一個線性組合即為第一個新變量，要求它在所有線性組合中方差最大，含有的信息量最多。如果第一個線性組合無法提取原始變量的所有信息，則考慮第二個線性組合即第二個新變量，且第一個新變量中所含有的信息不出現在第二個新變量中，即這兩個變量的協方差為零。繼續進行這個過程，直到包含的信息與原始變量包含的信息量相差不大。此過程即為主成分分析降維的過程，經過此過程可以使問題得到簡化[8]。

1.2 主成分分析基本理論

設所研究的問題包含個變量，可構成向量，協方差陣為，對做線性組合：

得到新的綜合變量，這里表示與之間的相關系數，所做的線性組合要求滿足以下條件：

（1）；（2） 與（）互不相關；（3） 是與不相關的所有線性組合中方差最大的。若滿足以上條件，則即為主成分，分別稱為原始變量的第1、第2、第個主成分，且對應方差依次遞減，通常選擇前幾個方差較大且所含信息總和達到以上的主成分。

每個主成分所含信息量的大小用方差來刻畫，要使的方差達到最大，即使達到最大，而協方差陣的特征值就是對應主成分的方差，特征值所對應的特征向量就是。是第個主成分的方差貢獻率，表示第個主成分提取個變量的信息量，該值越大，表示對應主成分所含信息量越多，為主成分的累計方差貢獻率，表示前個主成分所含原始變量的信息量。

1.3 利用主成分分析對成績評價的步驟

設個學生，成績有個變量，第個學生的第項成績為，則個學生個變量可構成原始數據矩陣為。

（1）對原始數據進行標準化，，其中，，。

（2）標準化數據后，計算相關系數矩陣，，其中。

（3）計算的特征值與相應的特征向量，因而可以得到個主成分。

（4）計算各個主成分的方差貢獻率與累計方差貢獻率，當前個主成分累計貢獻率達到80%以上，確定主成分的個數為。

（5）寫出綜合評價函數：，函數值即為學生綜合得分。

2 聚類分析

2.1 聚類分析基本思想

聚類分析是基于數據的相似性，根據數據的特征進行分類，聚合為一類的數據之間有較高的相似度，而類間的數據相似度較小。于是給定一組數據后，可以先確定度量數據之間相似程度的統計量，以此統計量為依據對數據進行劃分，把相似度較大的數據歸為一類，把另外的一些相似度較大的數據又歸為另一類，相似度大的歸到一個小的分類單位，相似度小的歸到一個大的分類單位，直至所有的數據都歸類完畢，把所有數據劃分后，就會形成一個由小到大的分類系統[2]。

K-means聚類算法

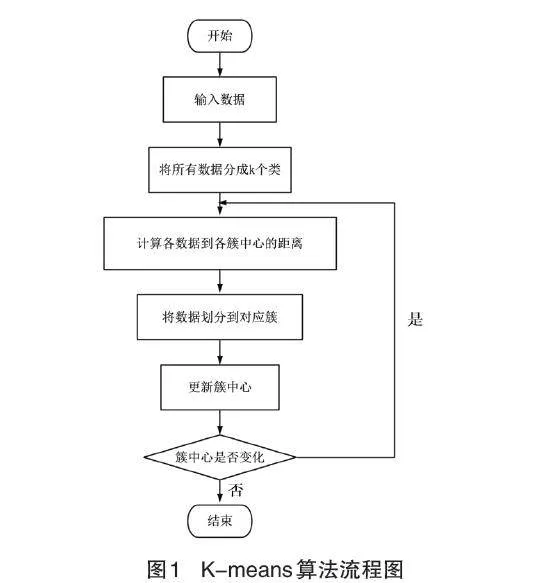
K-means聚類算法，屬于劃分聚類算法中的典型算法，是一種快速聚類法，相對其他算法具有操作簡便快捷的特點。K-means法中，首先要把全部數據分成k個類，把相似度高的數據劃分為一類，這樣就能得到類內相似度高，類間相似度低的幾簇數據。通過計算類中數據的平均值來確定相似度。K-means算法流程圖如圖1。

3 主成分分析與聚類分析在學生成績綜合分析中的應用

3.1 研究的基礎數據

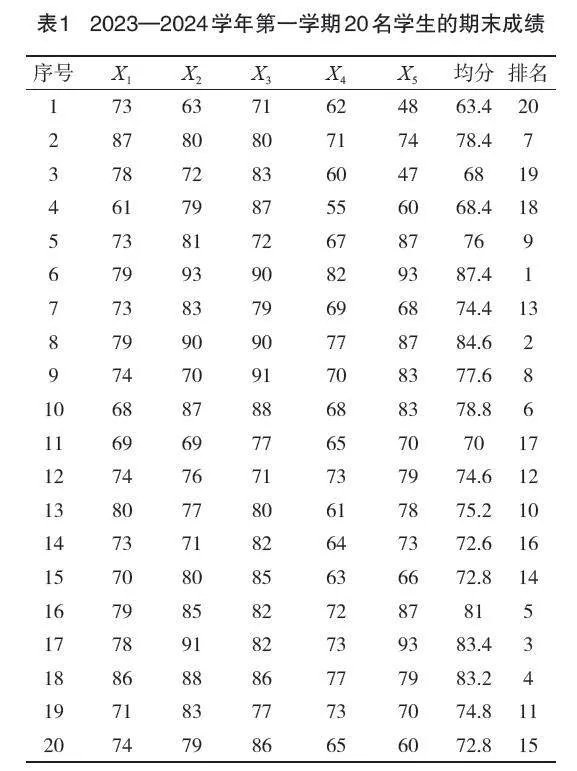
本文中研究的基礎數據來源于長治醫學院2023—2024學年第一學期某專業班級20名學生的5門課程期末成績，分別表示變量思想道德與法治、基礎化學、大學英語A、醫用物理學、醫用高等數學。如表1所示。

3.2 設計實現與實驗結果

使用R語言進行主成分分析得到結果，如圖2所示。

由圖2中的分析結果，在輸出的5個主成分中，前3個主成分的累計貢獻率已達89%，所以可用前3個主成分來進行分析。loading表示載荷，其值是 的系數，也是特征值對應的特征向量，由標準化變量所表達的主成分的關系式為：

由此得到綜合評價函數為

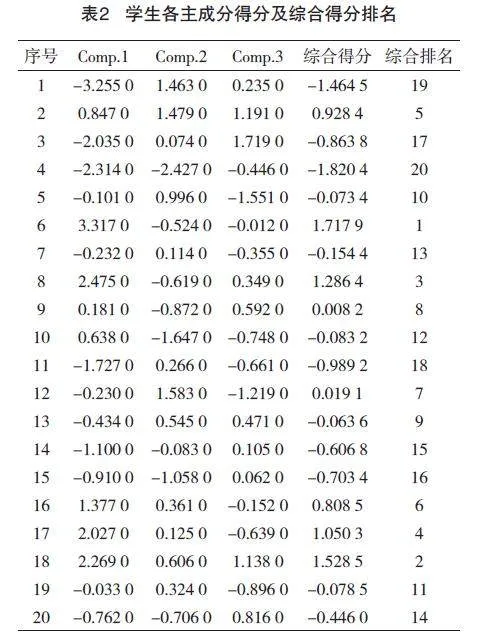
將成績數據代入得到表2中的3個主成分得分、綜合得分與排名，該結果是由統計分析得出，此過程很大程度上不受主觀因素的影響，因此用在實例分析上較合理客觀。

結果分析：由主成分分析得出的綜合排名與原始成績均值的排名相差不大，有極少數差異較大。例如序號為10號的同學，他的總分排名是6，而綜合排名是12，該同學在第一主成分得分較高，說明數學、物理、化學成績較好，在第二、三主成分得分較低，說明該生的思想道德與法治、大學英語成績并不好。序號為12號的同學，總分排名是12，而綜合排名是7，該生在第二主成分得分較高，第一、三主成分得分為負值。根據以上表中數據，能夠對學生在各課程上的學習情況有較客觀的了解與掌握，根據得分情況與綜合得分了解他們成績的特點，從而幫助分析學生的薄弱與優勢科目，進而提升教師的教學成效。

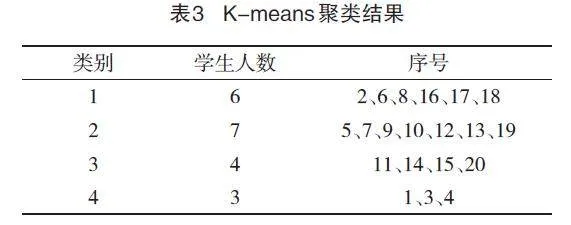
針對學生成績數據，依據前3個主成分得分，利用R語言進行K-means聚類分析，得到的結果如表3所示。

從表3可看出：將學生分為四類，第一類學生各科成績較理想，學習上較積極主動。第二類學生成績中等，有些同學成績或高或低，有偏科現象，在學習上積極主動性需要加強。第三類學生的第一主成分得分較低，數理化成績較不理想，要注重學習興趣的培養。第四類學生在各科成績上均不理想，之后要更多注重基礎知識的學習。

通過以上對主成分分析與聚類分析的思想、原理的闡述，以及對實驗結果的分析，可以看出，通過主成分分析與聚類分析來對學生成績劃分評定時，較傳統劃分方式更科學、合理，能更好地反映出學生的學習情況與教師教學成效。

4 結語

主成分分析與聚類分析作為當前最有應用前景的數據分析方法，已被廣泛應用于社會生活的各個領域。運用R語言通過主成分分析與聚類分析來劃分學生的成績，方便易行，且所得結果也具有合理性、有效性，這為教師開展教學工作與實踐提供有效的參考與指導，不斷提升教學質量。

對學生而言，學生可以認識到自身成績的類別，認清自己各科成績的差異，從而更有針對性地找到深入的方向，持續深造，提升自我。對教師而言，更清晰地了解學生的成績類別，結合學生的平時表現、學習背景進一步了解學生，從而因材施教，增強學生學習積極性與主動性。

個變量，可構成向量，協方差陣為，對做線性組合：，這里表示與之間的相關系數，所做的線性組合要求滿足以下條件：；（2） 與（是與不相關的所有線性組合中方差最大的。若滿足以上條件，則即為主成分，分別稱為原始變量的第1、第2、第個主成分，且對應方差依次遞減，通常選擇前幾個方差較大且所含信息總和達到的方差達到最大，即使達到最大，而協方差陣的特征值就是對應主成分的方差，特征值所對應的特征向量就是。是第個主成分的方差貢獻率，表示第個主成分提取個變量的信息量，該值越大，表示對應主成分所含信息量越多，為主成分的累計方差貢獻率，表示前個主成分所含原始變量的信息量。個學生，成績有個變量，第個學生的第項成績為，則個學生個變量可構成原始數據矩陣為。，其中，，。，，其中。的特征值與相應的特征向量，因而可以得到個主成分。與累計方差貢獻率，當前個主成分累計貢獻率達到80%以上，確定主成分的個數為。，函數值即為學生綜合得分。 （1）為所有數據與相應聚類中心的均方差之和；為數據對象中的一個數據；為類的均值。這個公式的聚類標準是要使每個聚類能具備以下條件：各類能盡量自行密集，而類間盡量分散。K-means算法流程圖如圖1。參考文獻

[1]龍鈞宇.基于均值聚類和決策樹算法的學生成績分析[J].計算機與現代化，2014（6）：79-83．

[2]葉福蘭.基于K-means均值算法的學生成績分析：以福州外語外貿學院信息管理與信息系統專業為例[J].貴陽學院學報（自然科學版），2017，12（3）：17-20.

[3]展金梅，陳君濤，田飛.數據挖掘技術在高校學生成績分析中的應用[J].科技資訊，2023，21 （19）： 202-205.

[4]李鳳英，許洪光，周方，等.基于數據挖掘和K-Means算法的高校學情數據集成研究[J].黑龍江工程學院學報，2022，36（4）：31-36.

[5]金玉.基于學習大數據的學生學習成績預測關鍵技術研究[D].南京：東南大學，2021.

[6]錢玲，饒江泉，羅小泉，等.基于成績分析探討知識背景對學習的影響[J].科技資訊，2023， 21 （9）： 234-237.

[7]郭繼東，鄭可晗，張晶，等.基于主成分分析的學習效果因素調查分析研究[J].機電工程技術，2022，51（5）：165-169.

[8]郭蘭蘭，付政慶，衣秋杰.主成分分析法在學生成績分析與評價中的應用[J].高教學刊，2021（3）：88-91.