基于改進和聲算法的叉車車間布局研究

摘 要：制造企業在生產效率低的原因之一是車間布局問題，因此科學合理的布局對制造企業來說尤為重要。以往車間布局多采用經驗布置，存在一定不足，本文以搬運成本最小和非物流關系最大為目標函數建立模型，并選擇改進和聲搜索算法對模型進行求解，得到最終布局方案，最后通過Flexsim軟件對改進前、后的車間進行建模仿真，結果表明改進的和聲算法在車間布局應用中取得了良好效果。

關鍵詞：改進和聲算法；車間布局；SLP；多目標優化；Flexsim

中圖分類號：TH 181" " " " 文獻標志碼：A

全球經濟一體化和制造業飛速發展對我國制造業的發展既是一種機遇，也是一個巨大的挑戰。在制造業發展過程中，生產和物流的聯系越來越緊密，優化生產物流的關鍵是合理的設施布局。合理的設施布局可以提高企業的生產效率并節約成本[1]。以往學者采用不同的優化算法與SLP方法結合，取得了良好效果，例如鄧兵等[2]采用SLP與遺傳算法相結合，改進了原有布局。丁祥海等[3]針對設施布置中存在的設施形狀不固定問題，提出了一種將GA算法與退火算法相結合的動態求解方法，顯著提高了設施利用率。

上述研究極大豐富了車間布局的相關理論，但是對于不同設施布局，其采用的目標函數和算法也具有極大差異，其中一些算法存在一定的局限性，容易陷入局部最優，因此本文采用一種改進的和聲搜索算法，對車間進行布局優化，并用仿真軟件驗證其有效性。

1 模型建立

1.1 目標函數

在目前的設施布局規劃問題中，單一目標函數的局限性不能滿足車間布局優化的多樣化需求，因此需要建立多目標函數模型。本文以最小搬運成本C和最大化非物流關系M為目標函數，構建車間布局模型。其中最小化搬運成本如公式（1）所示，其由作業單位間的搬運成本、搬運距離和搬運量的乘積計算得出；最大化非物流關系如公式（2）所示，其主要由作業單元間的非物流關系的緊密程度和關聯因子計算得出。

式中：n為生產單元的數量；cij為生產單元間i與j間的搬運成本；fij為作業單元i與j間的搬運量；dij為作業單元i與j間的距離，由曼哈頓距離表示，dij=|xi-xj|+|yi-yj|。

式中：n為車間中的作業單元數；Tij為作業單元i與j間的非物流關系的緊密程度；Bij為作業單元i與j間的非物流關系等級與距離的關聯因子。

為了便于處理，將多目標函數轉換為單目標函數，由于2個函數的量綱不同，因此需要對其進行標準化處理，分別如公式（3）、公式（4）所示。

式中：dmax為任意2個生產單元間的最大距離；cij為生產單元間i與j間的搬運成本；fij為作業單元i與j間的搬運量；dij為作業單元i與j間的距離；n為車間中的作業單元數。

式中：n為車間中的作業單元數；Tij為作業單元i與j間的非物流關系的緊密程度；Bij為作業單元i與j間的非物流關系等級與距離的關聯因子。

將公式（3）和公式（4）結合構成單目標函數，并引入加權因子f1和f2來調整2個目標函數所占的比重，其中f1+f2=1，轉化后的目標函數如公式（5）所示。

minX=f1C1-f2M1 （5）

式中：f1為搬運成本所占權重；f2為非物流關系所占權重。

1.2 約束條件

1.2.1 邊界約束

為保證目標函數得以求解，需要設置相應的約束條件，對車間的邊界進行約束，即任意2個生產區域的距離應當始終小于邊界區域，如公式（6）、公式（7）所示。

式中：xi和xj分別為任意作業單元i和j的X軸中心坐標；Li和Lj為作業單元i和j的長度；L為該車間的長度。

式中：yi和yj為任意作業單元i和j的Y軸中心坐標；Wi和Wj為作業單元i和j的長度；W為車間的寬度。

1.2.2 間距約束

除邊界約束外，為保證任意2個生產區域間沒有重疊，不同的生產區域間應當保留一定距離，間距約束如公式（8）和公式（9）所示。

式中：xi和xj分別為任意作業單元i和j的X軸中心坐標；Li和Lj為作業單元i和j的長度；s為作業單元i和j間的最小間隔距離。

式中：yi和yj為任意作業單元i和j的Y軸中心坐標；Wi和Wj為作業單元i和j的長度；s為作業單元i和j間的最小間隔距離。

2 改進和聲算法設計

和聲搜索算法是一種基于音樂演奏和聲原理的智能算法，和聲搜索算法產生于音樂創造過程中，模擬了音樂演奏中樂師調整每個樂器音調的，最終使樂器達到和聲最美的狀態[4]。和聲算法解決的問題主要是離散問題優化和非線性問題，而車間布局問題正是常見的離散優化問題，但是標準的和聲算法容易受聲庫、取值概率和微調概率的影響[5]。為解決該局限，本文提出一種結合遺傳算法、改進和聲算法的新方法，具體實施步驟如下。

2.1 初始化和聲庫

2.2 確定適應度函數

在遺傳算法中，種群中個體適應度越大，說明該個體越優秀。由于前提假設的是求最小值，因此設置適應度函數如公式（10）所示。

2.3 設定編碼方式

本文編碼采用實數編碼方式，實數編碼的樣式為[m1，m2，…，mn]，表示從車間的左下角開始，依次沿著X軸布置作業單位，如果同一行作業單位的長度之和超過車間總長度，就自動換行，得到最終布局圖。

2.4 創作新和聲

創作新和聲需要先初始化和聲記憶庫，在決策變量Xe中隨機生成HMS個和聲x1，x2，…，xHMS，再將和聲放入和聲庫HM。生成新和聲的方式如公式（11）所示。

式中：新和聲變量xe'以HMCR的概率選擇[0，1]中的任意一個值，反之，1-HMCR的概率選擇HM外的任意一個值；rand1為均勻分布在[0，1]的隨機數。

2.5 更新和聲庫

如果新的和聲xe'來自HM，就對其進行音調微調，隨機生成均勻分布在[0，1]的隨機數rand2。當rand2lt;PAR時，將遺傳算法的變異代替和聲算法的微調帶寬，反之不調整。具體操作如下所述。

2.5.1 選擇操作

以個體適應度為依據選擇個體進行遺傳操作，從舊的種群中使用輪盤賭法選擇適應度高的染色體，為以后染色體交換、變異并產生新的染色體做準備[6]。其中染色體被選中的概率Pr如公式（12）所示。

式中：xe為種群中第e個染色體；f（xe）為第e個染色體的適應度值；∑ f（xe）為種群中所有染色體適應度值之和。

2.5.2 交叉變異

交叉是指在自然界繁殖中由染色體的交換組成新的品種，遺傳算法中的交叉運算是指根據一定的交叉概率Pc對2個相互配對的染色體交換部分基因，從而形成新的個體[7]。本文將多點交叉作為交叉算子，變異算子可以維持染色體的多樣性，提高算法的局部搜索能力，其基本思想如下：在編碼長度內隨機生成2個位置a和b，對2個位置間的基因進行逆序變換，從而增強和聲搜索算法的整體尋優能力。

3 算例分析

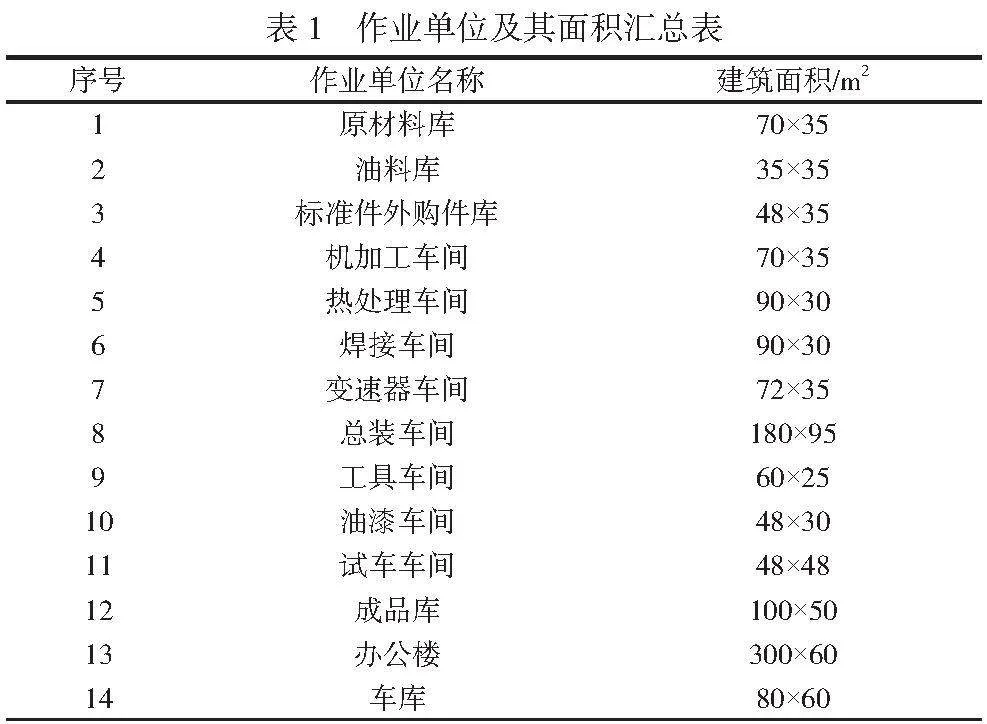
以A企業為例，已知該企業的生產車間共有14個區域：1原材料庫；2油料庫；3標準件外購件庫；4機加工車間；5熱處理車間；6焊接車間；7變速器車間；8總裝車間；9工具車間；10油漆車間；11試車車間；12成品庫；13辦公樓；14車庫。擬布局的車間長600m，寬300m，各單位所占面積見表1。

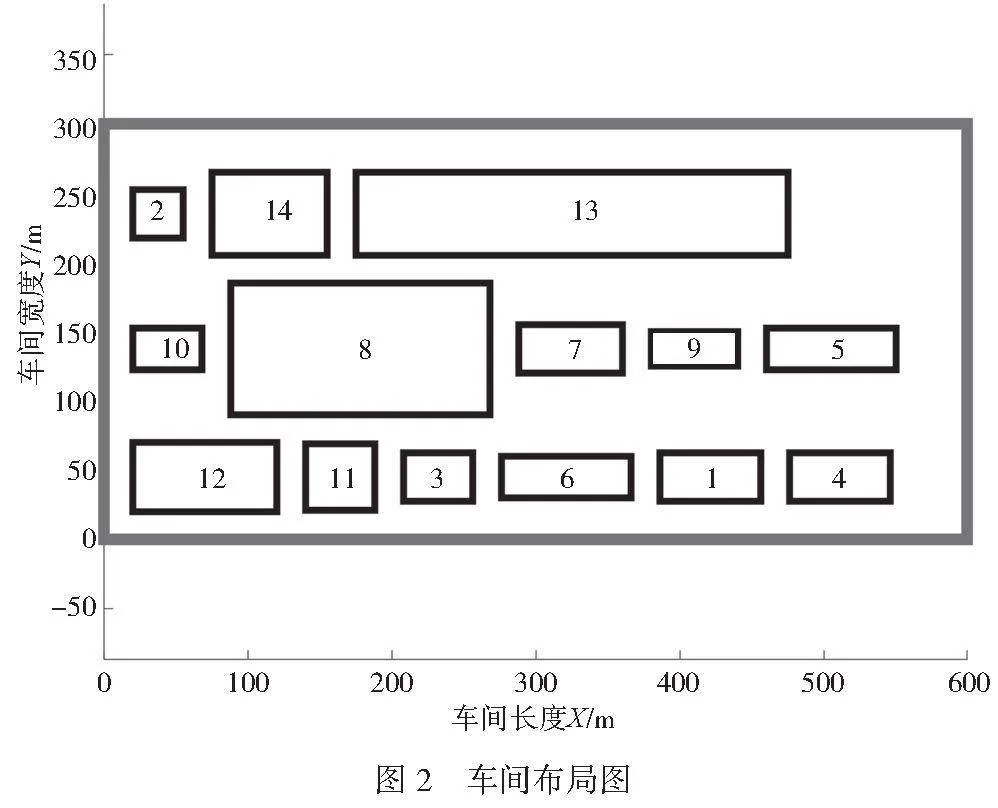
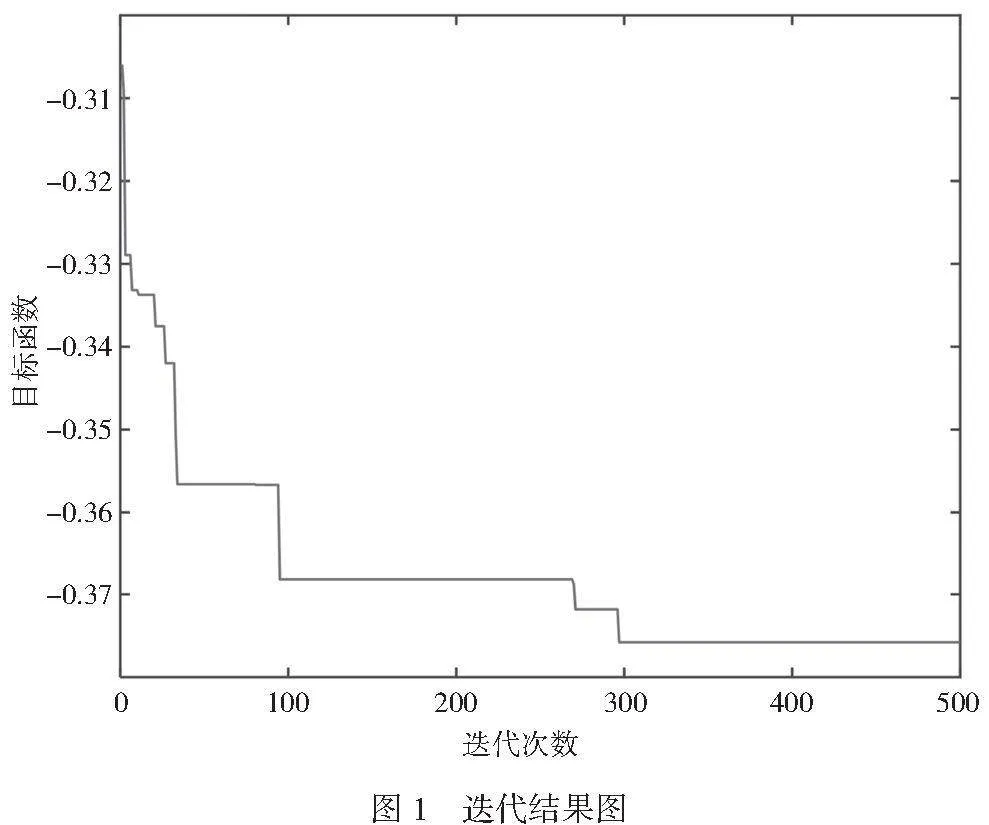
根據專家打分設置上述算例中的目標函數的權重，其中f1=0.5，f2=0.5。將和聲記憶庫的大小HMS設置為100，音調微調概率PAR設置為0.2，和聲記憶庫的取值概率HMCR設置為0.96，迭代次數Tmax設置為500，遺傳算法中交叉概率Pc設置為0.95，變異概率Pm設置為0.1。利用MATLAB進行500次迭代，所得迭代結果曲線和布局結果分別如圖1和圖2所示。

過進一步對初始布局和改進后布局的目標函數進行計算，結果見表2。結果表明，新布局的運輸成本比原布局降低了24.2%，非物流關系提升了23.7%。

4 Flexsim仿真

雖然使用SLP方法和改進和聲算法改進了A車間布局，使運輸成本和非物流關系達到最優，但是生產系統是一個復雜的動態隨機系統[8]，僅靠算法求解的結果很難體現各要素間的相互作用，因此本文采用Flexsim仿真，建立A公司車間布局仿真模型并輸出仿真報告，進一步驗證改進的有效性。

分別將改進布局和原始布局的布局圖分別按照1∶1的比例代入Flexsim中，在搭建模型的過程中，選擇相應的實體并設置相應的動態參數。

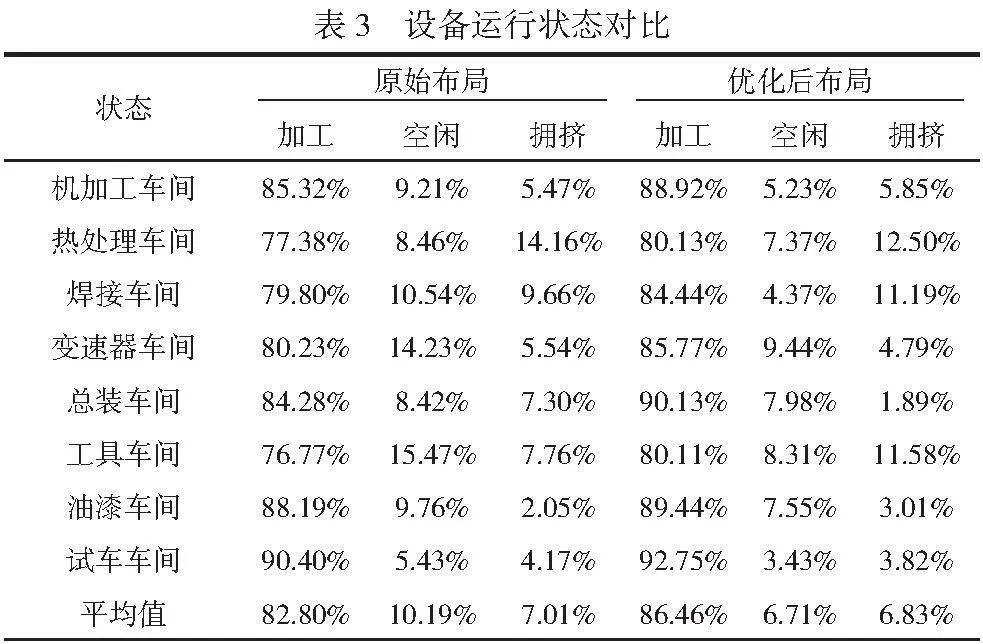
為判斷改進后的布局是否合理改進，本文將設備工作狀態作為觀測結果，生成各個車間設備的工作狀態，見表3。比較原始布局和優化后的布局可知，原始布局的設備平均加工時間約為82.80%，平均空閑時間約為10.19%，平均擁擠時間約為7.01%，優化后布局的設備平均加工時間為86.46%，比原始布局提升3.66%，平空閑時間約為6.71%，比原布局降低3.84%，平均擁擠時間約為6.83%，比原布局降低了0.18%。可見從設備運行狀態來看，改進后的布局比原始布局效果更好。

5 結論

本文針對車間布局問題建立模型，設置運輸成本最小化和非物流關系最大化2個目標函數，采用改進和聲算法對A車間進行優化布局，得到最優布局方案，最后利用仿真軟件Flexsim驗證布局的可靠性。結果表明，改進和聲算法在車間布局中取得了良好效果。

參考文獻

[1]姚明釗，陳鵬飛，裴小兵.基于SLP和改進遺傳算法優化C企業車間布局[J].有色金屬工程，2023，13（9）：99-109.

[2]鄧兵，林光春.改進SLP和遺傳算法結合的車間設備布局優化[J].組合機床與自動化加工技術，2017（8）：148-151，156.

[3]丁祥海，韋新立，姚文鵬.考慮柔性面積需求的動態設施布局方法研究[J].工業工程與管理，2018，23（5）：116-125.

[4]鄭廣輝，錢葉昶，劉鵬，等.基于遺傳和聲算法的復興號部件生產車間布局研究[J].機床與液壓，2023，51（4）：57-62，66.

[5]張青雷，黨文君，段建國.基于自適應遺傳算法的大型關重件車間布局優化[J].機械設計與制造，2021（1）：236-239.

[6]張思奇，于登輝，鄭一明，等.基于多目標候鳥算法的車間布局研究[J].現代制造工程，2022（2）：16-23.

[7]王俊杰，蔡蕓，熊禾根.基于遺傳算法的雙層車間設施布局優化研究[J].物流科技，2023，46（11）：53-56.

[8]邢彩虹，劉剛，胡曉兵，等.基于SLP改進遺傳算法的多區域單雙行設備布局優化方法[J].四川大學學報（自然科學版），2022，59（5）：70-78.