基于門限自回歸模型對人民幣匯率波動的研究

摘 要：人民幣匯率的波動受多方面因素的影響，為研究人民幣匯率的波動情況，進一步預測人民幣匯率的變化，本文以2011年1月—2023年12月的人民幣兌美元的匯率中間價的月度數據作為研究對象，分別建立了求和自回歸滑動平均模型和門限自回歸模型，并對兩種模型的預測結果進行對比。結果表明：人民幣匯率的波動具有非線性特征，并且門限自回歸模型比求和自回歸滑動平均模型準確度更高，在未來幾個月人民幣兌美元中間價略有下降，但能夠維持在相對穩定水平，人民幣略有升值。

關鍵詞：求和自回歸滑動平均模型；門限自回歸模型；人民幣匯率；股份指數；ARIMA模型

中圖分類號：F822；F037.1 文獻標識碼：A 文章編號：2096-0298（2024）12（a）--06

在日常生活中，以時間為一個序列，通過利用事物發展的延續性，結合已有數據，可以預測事物將會發生的趨勢。最早開始興起的是線性自回歸（AR）模型，但隨著研究的深入，人們發現自回歸模型在處理一些實際問題時具有局限性，大量宏觀經濟序列存在非線性動態調整的特征，在經濟預測中，增長率、通貨膨脹率、失業率等在不同商業周期呈現出不同的動態調整機制[1]，在資產定價中，股票價格、匯率、利率等金融時間序列均具有非線性的特點，這時使用自回歸模型進行建模不再合適。

把ARMA模型推廣到允許其AR多項式以1作為特征根，則模型變成求和自回歸滑動平均模型。求和自回歸滑動平均模型（Autoregressive Integrated Moving Average Model，簡稱ARIMA模型）是一種單位根非平穩的模型，慣用的方法是對其進行差分化處理，使其變為平穩的時間序列模型，進一步可應用ARMA模型研究其相應性質。

門限自回歸模型（Threshold Autoregressive Model，TAR）是一種非線性模型[2]，最初由H. Tong和Lim在1978年提出[3]，旨在處理具有明顯非線性特征的時間序列數據，其思路是將非線性的時間序列劃分成多個區間，在每個區間內建立線性的自回歸模型，利用門限的控制作用，保證了模型的穩定性和廣泛適用性，與多元線性回歸、模糊分析、灰色模型等預測模型相比，門限自回歸模型更具有穩定性和適用性[3]。

門限自回歸模型廣泛應用于多個領域，在經濟預測方面，有劉玉鳳等（2014）[4]、石自忠等（2014）[5]所研究的牛肉與羊肉的價格預測，利用兩門限自回歸模型對價格同比指數序列進行分析；在資產定價中，有周連強（2016）[6]以上海股票市場和深圳股票市場的每日收盤指數作為研究對象，探討兩種股份指數序列的非線性特征；同時，在匯率的非線性研究中，劉譚秋（2007）[7]利用線性的自我激勵閾值自回歸模型擬合人民幣實際匯率歷史數據，靳曉婷等（2008）[8]利用不同時間段匯率數據建立了門限自回歸模型，得出結論：2005年7月—2008年1月的人民幣匯率波動存在非線性特征。

匯率的波動會通過作用進出口商品的價格，通過各種途徑影響到居民的消費行為，匯率的短期預測對國家出臺相關貨幣政策、財政政策均具有重要意義，對企業的進出口、投融資具有指導價值。

在對人民幣匯率波動的研究中，鐘大勇和張恒（2021）[9]采用廣義自回歸條件異方差GARCH模型對人民幣匯率的波動進行研究，李明軒和俞翰君（2020）[10]采用自回歸滑動平均ARMA模型與GARCH模型、EGARCH模型、TGARCH模型和GARCH-M模型對數據的波動性進行研究；王藝柳（2024）[11]將求和自回歸滑動平均ARIMA模型與廣義自回歸條件異方差GARCH模型進行組合建模，改良了ARIMA模型的預測準確度；康寧，劉霆（2022）[12]通過建立門限分位數自回歸TQAR模型深入研究人民幣匯率的波動情況，研究結果表明人民幣匯率具有兩階段的非線性特征，同時呈現典型的異質性；蘇玉華（2012）[13]比較了TAR模型、ARIMA模型及GARCH模型對人民幣匯率預測的準確度，認為TAR模型更具優勢。

本文以2011年1月—2023年12月的人民幣兌美元的匯率中間價作為研究對象。首先，介紹ARIMA模型和TAR模型的相關理論知識；其次，分別應用ARIMA模型和TAR模型對取對數后的匯率中間價進行建模和預測；再次，比較ARIMA模型與TAR模型的預測結果，選出TAR模型作為最終應用模型；最后，根據預測結果，給出相應的分析結果與建議。

1 理論基礎

1.1 ARIMA模型

ARIMA模型作為一種基本平穩時間序列模型得到了廣泛應用。但現實問題中，觀測序列{Xt}可能不是平穩序列，此時不能應用ARMA模型進行建模，需對模型進行平穩化處理。序列差分后變為平穩的時間序列，差分后的序列則可應用ARMA模型進行建模。此時原序列則為ARIMA模型。

求和自回歸滑動平均模型（Autoregressive Integrated Moving Average Model），簡稱ARIMA模型，結合了AR模型與MA模型，可以更好捕捉到變化趨勢。該模型可表示為：

并記為ARIMA（p，d，q），其中c為常數項，d，ai，bj是差分階數，AR模型和MA模型的參數，εt為誤差項。

ARIMA模型建模流程：第一步，對序列進行平穩性檢驗和白噪聲檢驗，如果序列非平穩，但經過差分后序列平穩且非白噪聲，則進行下一步，此步可以確定ARIMA模型中的未知量d；第二步，通過觀察自相關系數圖和偏自相關系數圖進行模型識別和參數估計；第三步，對構造的模型進行檢驗；第四步，根據構造模型進行模型預測。

1.2 TAR模型

為限自回歸模型[14]，并記為TAR（l，d;τ1，…τi-1;p1，p2，…，pl）中τj， j=1，2，…，l-1限值，l為門限區間的個數，d為延遲步數。a0（j），pj分別為第j個門限區間的內自回歸模型的系數和階數。

在建立TAR模型前首先需要進行非線性檢驗，其基本思想是：在線性假設下，一個合適確立的線性模型的殘差應該是獨立的，任何對殘差獨立性的違背都說明現有模型包括線性的假設不合適[15]。

建立TAR模型的關鍵在于確定門限區間的個數l、門限值τ1，τ2，…，τl-1遲步數d，通過對門限個數l，門限值τ1，τ2，…，τl-1遲步數d尋優確定模型參數。

1.3 三類常見的門限自回歸模型

常見門限自回歸模型（TAR）有單門限、雙門限和三門限模型。

1.3.1 單門限自回歸模型

單門限自回歸模型即l=2，門限值為τ1，由于不同門限區間可能有不同的自回歸系數和階數，故a0（1），p1記為第1個門限區間內的系數和階數，a0（2），p2記為第2個門限區間內的系數和階數，故單門限自回歸模型可以表示為

1.3.2 雙門限自回歸模型

雙門限自回歸模型，即l=3，門限值為τ1，τ2，雙門限自回歸模型可以表示為

1.3.3 三門限自回歸模型

三門限自回歸模型，即l=4，門限值為τ1，τ2，τ3，三門限自回歸模型可以表示為

在實際應用中，建立門限自回歸模型時，門限個數往往選擇1個、2個或3個，因為門限個數越多越復雜，越容易導致過擬合現象，在理論部分不限制門限個數。本文實證分析部分考慮用單門限自回歸模型對相應數據進行建模和預測。

2 實證分析

2.1 數據來源

人民幣匯率中間價的變動情況，尤其是對美元的匯率中間價，是觀察人民幣匯率走勢的重要指標。本文實證分析使用國家外匯管理局給出的數據，標價方法為直接標價法，其含義為100美元所兌人民幣數量。這個價格對于指導市場預期、影響外匯交易及宏觀經濟政策都有重要作用。

數據樣本選擇2011年1月—2023年12月的人民幣兌美元的匯率中間價的月平均值{Xt}建模數據，為減少數據波動，對數據全部采取對數化處理，生成新的數據 {lnXt}。

2.2 建立ARIMA模型

建立ARIMA模型之前，首先需對模型進行平穩性檢驗。

2.2.1 平穩性檢驗

平穩性檢驗的方法包括時序圖判別法、自相關系數檢驗法、分段檢驗法、單位根檢驗法等。本文只介紹自相關系數檢驗法。自相關系數檢驗法的原理是：平穩的時間序列是具有短期相關性的，其自相關系數表現為截尾、拖尾的情形，即自相關系數會隨著延遲期數的增加快速的變為零或以指數形式向零衰減。

序列的自相關系數圖隨著滯后階數的增加快速下降為0，該序列為平穩序列（此處省略了其自相關系數圖）。

2.2.2 模型建立

本文利用EViews10軟件，對ARIMA模型進行定階，得到ARIMA（1，0，1）到ARIMA（19，0，1）共38個建模結果，通過比較每個模型對應的AIC值，得到最優模型為ARIMA（1，0，1），也就是模型估計為

lnXt=0.112+0.983lnXt-1+0.456εt-1（6）

TAR模型為本文主要考慮的模型，此部分省略了ARIMA模型的模型檢驗與模型預測部分，感興趣的讀者可自行進行檢驗和預測。

2.3 建立TAR模型

2.3.1 非線性檢驗

門限自回歸模型適用于非線性的時間序列，故在建模前，對時間序列進行非線性檢驗，以保證該序列適用門限自回歸模型。非線性檢驗包括參數和非參數統計量。非線性檢驗的基本思想是：在線性假設下，一個合適確立的線性模型的殘差應該是獨立的，任何對殘差獨立性的違背都說明現有模型包括線性的假設不合適，所以通過觀察殘差、殘差平方和的自相關系數圖和偏自相關系數圖可以確定殘差序列是否具有非線性特征，在顯著性水平為α=0.05，如果P值小于0.05則認為殘差序列具有自相關性，即存在非線性特征。

通過觀察時間序列圖有助于發現時間序列的非線性特征，也可通過觀察現有模型的殘差和殘差平方和的自相關系數圖和偏自相關系數圖判斷是否具有非線性特征。這里對于通過時間序列圖觀測非線性特征部分不做贅述。

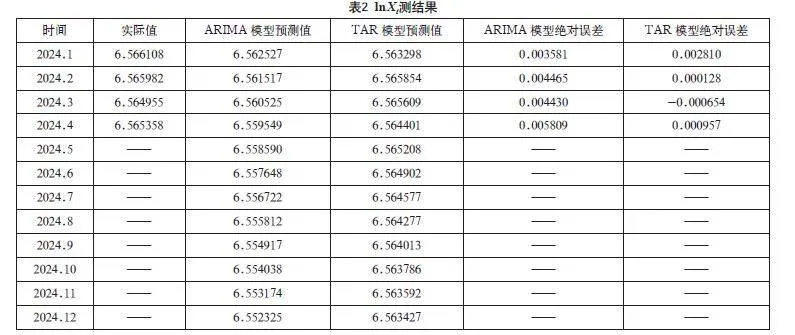
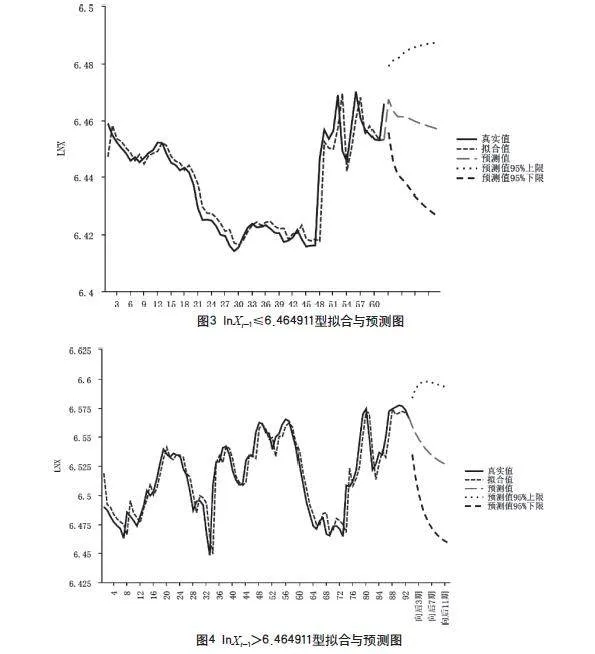
本文嘗試對時間序列建立AR（2）模型，通過觀察AR（2）模型的殘差和殘差平方和的自相關系數圖和偏自相關系數圖（圖1、圖2）可以看出存在P<0.05，即殘差之間存在自相關，故該序列具有非線性特征。

2.3.2 模型建立

建立TAR模型的關鍵在于確定門限區間的個數l、門限值τ1，τ2，…τl-1遲步數d，這是對門限個數l，門限值τ1，τ2，…τl-1遲步數d的尋優過程。在每個門限區間，還需確定AR模型的階數p1，p2，…pl數尋優時，可采用AIC準則來選擇模型階數和最優參數。因此，AIC是所有2l+1個參數的函數，即

AIC=f （p1，p2，…，pl，l，d，τ1，τ2，…τl-1）（7）

使AIC值達到最小參數，即最終的TAR模型的參數。

對于確定的時間序列{Xt，t=1，…，N}AR模型的常用參數估計方法具體步驟如下所示[14]：

（1）確定區間個數l、延遲步數d和每個區間AR模型階數p1，p2，…pl界L，D和P。其中，p1，p2，…pl每個pj的上界均可以不同，但為了方便起見，選擇公共的上界P，并且所確定區間個數一般為1～3個，即L不超過3。

（2）給出門限值τ1，τ2，…τl-1值，由于門限值的確定過程是逐步尋優過程，可將已有的時間序列取值從小到大排列，分別取0.3n，0.4n，0.5n，0.6n，0.7n所對應的值為門限值，從而確定（-∞，+∞）的剖分{Ωj}。

（3）把序列{Xt，t=1，…，N}按照Xt-d落在剖分{Ωj}中的情況分為l組。

（4）對于落在第j（1≤j≤l）個區間內的序列，建立AR模型如下：

分別令其階數pj取值從1增大到P，可以得到AR模型的參數ai（j）， j=0，1，…，pj機誤差εt（j）的方差、AIC值，令AIC為P個AIC值中的最小值，相應的區間的AR模型的階數，從而得到每個區間適用的AR模型。

對于落在第j（1≤j≤l）個區間內AR模型的參數可由最小二乘法、矩估計和最大似然估計方法得到。

（5）各區間確定最小AIC值為AIC可以得到整個時間序列模型的最小AIC值之和為：

（6）對門限值尋優：固定門限個數l和延遲步數d，按照迭代算法對確定的門限值τ1，τ2，…τl-1，每次迭代時，重復步驟3～5，并計算模型的AIC值，使得AIC值達到最小的參數值為給定l和d時的估計值，相應AIC值記為。

（7）對延遲步數尋優：固定門限個數l，讓d從1增大到D，重復步驟3～6，使得最小的d即為估計值應的AIC值記為。

（8）對門限個數尋優：讓l從2增大到L，重復步驟3～7，使得最小的l，即為估計值而得到每個參數的估計值。

在上述估計過程中，依次估計模型的不同參數，即先確定門限值τ1，τ2，…τl-1的估計值給定的情況下再確定延遲步數d的估計值后確定門限個數l的最佳取值。

本文考慮對建立單門限自回歸模型，即門限區間個數為l=2，即門限值個數為1，延遲步數上界D=2，每個區間AR模型的階數上界P=3。將樣本數據從小到大進行排列，分別選擇0.3n、0.4n、0.5n、0.6n、0.7n所對應的值作為門限候選值τ1，對于每一個確定的延遲步數，均可以得到5個門限值，如表1所示。

利用延遲步數d=1和d=2時的10個門限值分別確定剖分{Ωj}， 把序列{Xt，t=1，…，N}按Xt-1和Xt-2落在剖分{Ωj}中的情況分為2組，對以上區間的數據分別建立AR（1），AR（2），AR（3）模型，可以得到AR模型的表達式，并計算AIC值。

通過迭代法，延遲步數d=1時，最優門限值為τ1=6.464911，此時AIC（2，1，6.464911），AIC（2）=-543.170；延遲步數d=2固定時，最優門限值為τ1=6.45107時AIC（2，2，6.45107）=-944.866，AIC（1）=-334.636，AIC（2）=-610.230。

因為AIC（2，1，6.464911）<AIC（2，2，6.45107）最優延遲步數為d=1，最優門限值為τ1=6.464911，得到預測方程：

2.3.3 模型檢驗

模型的檢驗包括兩種：

（1）對模型的有效性進行檢驗。合適的擬合模型應該能提取觀測序列幾乎所有樣本的信息，即殘差序列應為白噪聲序列。

（2）對參數的顯著性進行檢驗。對于參數aj的檢驗，其原假設和備擇假設分別為，檢驗統計量為：

在給定的顯著水平α下，如果P<α，則可以1-α的置信水平拒絕原假設，認為該模型參數顯著；反之則該模型不顯著。

2.4 模型預測

根據以上得出的ARIMA模型（1）和單門限自回歸模型（2），可以得到預測結果（表2）。

由表2可得兩個模型的預測結果，并得到ARIMA模型的平均絕對誤差值為0.004571，TAR模型的平均絕對誤差值為0.003241，TAR模型的預測準確性更高。

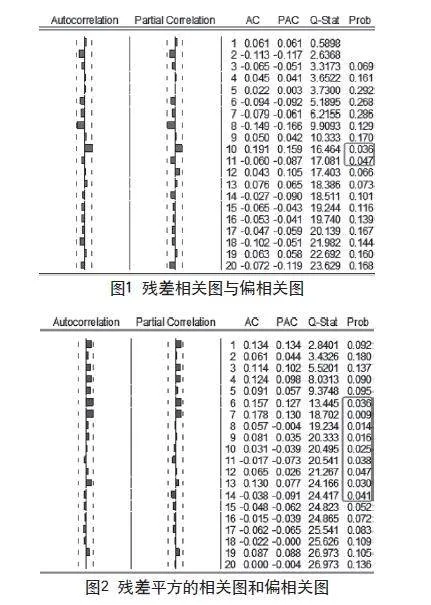
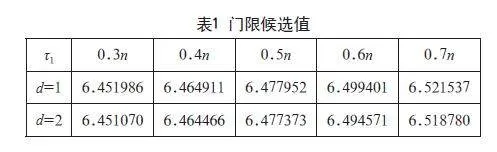
根據式（2）給出了模型的預測方程，可以得到模型的擬合與預測圖，當lnXt-1≤6.464911合圖為圖4，當lnXt-1> 6.464911合圖為圖5。

通過圖3和圖4可以看出，預測值和實際值擬合效果較好，通過表2可以看出，預測值的絕對誤差較小，說明該預測模型比較合適。

通過表2預測結果可以看到，2024年5月人民幣兌美元中間價為709.959552，6月人民幣兌美元中間價為709.742338，7月人民幣兌美元中間價為709.511709，8月人民幣兌美元中間價為709.299889。從短期來看，人民幣兌美元中間價較2024年初有所下降，人民幣升值，但整體維持在相對穩定的水平，更有利于中國的經濟和金融市場的穩定發展。

3 結語

本文基于門限自回歸模型的基本理論，研究了人民幣匯率的波動預測模型，匯率的波動會通過作用進出口商品的價格，通過各種途徑影響到居民的消費行為[16]，預測人民幣匯率的波動并及時做出相應政策調整，有利于企業和國家的進一步發展。

通過對人民幣匯率的研究表明，在未來3個月，人民幣兌美元中間價略有下降，但將繼續穩定在合理均衡水平，人民幣略有升值。有相關專家認為這歸因于以下三個方面[17]：首先，2023年12月以來，通貨膨脹壓力減輕，全球多國央行停止加息，開啟降息周期，美元指數或繼續回落，人民幣升值；其次，美國經濟顯現出韌性，中美貨幣政策仍存在一定程度的錯位；最后，人民幣匯率中間價逆周期因子釋放信號，當前在岸及離岸匯率較人民幣中間價偏離幅度較大，中間價或在美元強勢之下被動調整。

人民幣匯率變化首先對進出口的影響最大，人民幣升值，對于等值的外幣會兌換更少的人民幣，相關文獻[18]認為人民幣升值會抑制我國企業的出口。其次，貨幣政策也會隨著人民幣匯率的變化而改變，人民幣升值，貨幣政策將延續強化逆周期和跨周期調節思路，繼續加大對實體經濟的支持，刺激消費、擴大內需[19]。人民幣升值還有利于擴大國內群眾對進口產品的需求、增加居民消費的多樣性，減輕企業進口的成本，同時會對出口企業產生不良影響，有利于“倒逼”國內企業產業結構轉型升級。

參考文獻

聶思玥.門限自回歸模型的理論與應用研究[D].南京：南開大學，2014.

孟慶斌，周愛民，靳曉婷.基于TAR模型的中國股市價格泡沫檢驗[J].南開經濟研究，2008（4）：46-55.

張亮.門限自回歸（TAR）模型及其在匯率波動問題中的研究[D].蕪湖：安徽工程大學，2013.

劉玉鳳，王明利，石自忠.基于門限自回歸的我國羊肉價格波動分析[J].廣東農業科學，2014，41（17）：206-210.

石自忠，王明利，胡向東.我國牛肉價格波動的門限及政策研究[J].中國農業大學學報，2014，19（4）：200-205.

周連強.TAR模型在滬深股票市場研究中的應用[J].商業時代，2010（21）：72-73.

劉潭秋.人民幣實際匯率的非線性特征研究[J].數量經濟技術經濟研究，2007（2）：11-18.

靳曉婷，張曉峒，欒惠德.匯改后人民幣匯率波動的非線性特征研究： 基于門限自回歸TAR模型[J].財經研究，2008，34（9）：48-57.

鐘大勇，張恒.基于GARCH模型的人民幣匯率波動研究[J].中國物價，2021（10）：24-26.

李明軒，俞翰君.基于ARMA—GARCH模型的人民幣匯率波動性研究[J].時代金融，2020（33）：1-3+8.

王藝柳.基于ARIMA-GARCH模型的人民幣匯率波動研究[J].中國商論，2024（11）：9-12.

康寧，劉霆.基于門限分位數自回歸模型的人民幣匯率波動及預測研究[J].阜陽師范大學學報（自然科學版），2022，39（2）：24-32.

蘇玉華.人民幣匯率預測模型與實證研究[J].時代金融，2012（26）：11-12.

周永道，王會琦，呂王勇.時間序列分析及應用[M].北京：高等教育出版社，2015.

Ruey S. Tsay.王輝，潘家柱.金融時間序列分析（第二版）[M].北京：人民郵電出版社，2009.

王姝睿.[2024年匯市展望]人民幣匯率2023年“先抑后揚”2024年有望繼續升值[Z].https：//finance.sina.com.cn/money/forex/rmb/2024-01-03/doc-inaafauh4685461.shtml，2024-1-3.

姚進.人民幣匯率保持基本穩定有堅實基礎[N].經濟日報，2024-3-28（11）.

金朝輝，朱孟楠.人民幣實際匯率變動對出口貿易的影響[J].國際貿易問題，2021（5）：143-160.

溫彬，張麗云，韓思達，等.關注央行的“新提法”： 2024年一季度貨幣政策執行報告解讀[Z].https：//finance.sina.com.cn/jjxw/2024-05-14/doc-inavestp4338313.shtml，2024-5-14.