基于機器學習的自動化生產線故障預警研究


摘 要:本文旨在探討基于機器學習的自動化生產線故障預警系統,根據選礦廠實際生產數據進行試驗驗證,并評估不同核函數在支持向量回歸(SVR)中的性能。本文將SVR作為關鍵算法之一,在模型訓練階段利用歷史數據對SVR模型進行訓練,并調整超參數以達到最佳狀態;在實時推理過程中,運用經過訓練的SVR模型對新收集的實時數據進行推斷與故障預警操作。模型使用選礦廠真實數據集進行試驗驗證,分別采用線性核函數、多項式核函數和徑向基核函數構建預測模型。結果顯示,徑向基核函數在捕捉復雜非線性關系方面表現優異。
關鍵詞:機器學習;支持向量回歸;故障預警
中圖分類號:TP 393" " " " 文獻標志碼:A
隨著工業自動化程度不斷提高,自動化生產線在制造業中具有至關重要的作用。由于設備運行狀態復雜多變,因此故障預警成為保證生產效率和產品質量的關鍵環節。傳統基于規則或閾值判定的故障檢測方法無法兼顧系統復雜性和實時性需求,在處理大規模數據過程中表現不佳,因此更多研究者從機器學習的視角進行分析。陳國健等利用堆棧自編碼器和Softmax分類器研究了基于自編碼的長流程造紙過程斷紙故障識別[1]。關曉晴等利用多源域數據與機器學習算法,根據振動信號特征構建高維混合特征空間,進行轉子不平衡故障診斷[2]。黃穎祺針對大數據用戶側異常情況,提出基于機器學習的異常數據診斷框架,并探索了4種無監督學習在線異常檢測方法[3]。朱宏偉等使用少量傳感器融合機器學習技術進行氣動系統并聯雙氣缸泄漏故障診斷[4]。趙丹等針對礦井通風系統不平衡樣本集問題,設計了面向通風系統不平衡數據集的WGAN-div-RF故障診斷模型[5]。王加昌等比較了各類代表性剩余使用壽命預測模型在NASA渦扇發動機仿真C-MAPSS上的性能表現[6]。
1 預警算法構建
礦石選礦旨在根據礦石中不同礦物的物理化學性質采用不同方法分離金屬鐵與無用脈石。該過程涉及多個加工工序,需要經過并聯和串聯交替處理,才能得到最終的精礦產品,生產線體系復雜,因此其生產線管理從生產線傳感器和設備實時數據中進行數據采集。這些數據包括各種工藝參數、溫度和壓力等信息。傳感器提供的實時數據不僅可以用于監控每個生產活動本身,以保證其正常運行,還可以應用于對整條自動化生產線進行綜合評估和故障預警。
在基于機器學習算法構建預警系統方面,算法將支持向量回歸(SVR)作為關鍵算法之一,尋找最佳超平面并進行回歸分析。對于一組隨機樣本,假設其僅具有2種維度,相應構成散落在平面內的點,如公式(1)所示。
D=(x,y) " " " " " (1)
式中:D為一個指定樣本,即特定時間點的設備狀態信息;x和y均為其參數。
x 、y在平面上呈現為橫縱坐標值,對簡化的二維平面來說,D僅有2項參數。假設平面內存在2類點,也即模型的分類目的。基于此構建2條直線,分別如公式(2)、公式(3)所示。
?x+=k1 " " " "(2)
?x+=k2" " " "(3)
式中:為給定分類直線的法方向;x為函數橫坐標值,用于描述直線特征;為偏置項,決定了分類直線與原點的距離;k1與k2均為定義直線的額外變量。
調整后,使這2條直線如公式(4)、公式(5)所示。
?x+=-k" " " " (4)
?x+=k" " " "(5)
因此中間線可表示為公式(6)。
(w?x)+b=0 " " " (6)
式中:w為分類直線法方向;b為分類直線截距。
將其距離記作,即間隔為。由此,分類問題轉化為一個關于b和w的最優化問題。將這一過程推廣至一般的n維空間,如公式(7)所示。
(7)
式中:為求解n維空間內最優化目標函數;s.t.為使什么得到滿足;yt為超平面截距;w*為空間內分類超平面法方向;b*為超平面切基準截距;xi為第i項特征的輸入變量。
其劃分平面相應升為n維空間中的超平面,如公式(8)所示。
(w*?x)+b*=0 (8)
該SVR模型將n維條件下的分類問題轉化為決策優化問題,即為sgn((w*·x)+b),其中sgn為根據輸入數據點判斷其所屬類別的函數。
由此,算法區分故障與非故障的2類典型信息,需要利用相關參數信息進行預測。具體來說,在模型訓練階段,利用歷史數據對SVR模型進行訓練,并調整超參數以達到最佳性能狀態。進而在實時推理過程中運用經過訓練的SVR模型對新收集的實時數據進行推斷與故障預警操作。根據輸出結果判斷是否存在潛在故障或異常情況,并觸發相應措施或報警通知人員處理問題,由此構成基于機器學習算法的自動化生產線故障預警機制。
2 試驗驗證
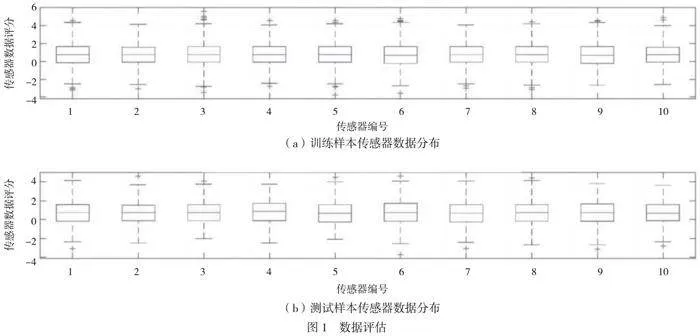
在試驗驗證階段,本文使用來自某選礦廠生產過程中的實際數據進行模型訓練和測試。隨機選取10個傳感器數據,設定50%樣本偏移為異常條件,以70%與30%的比例隨機抽取構成訓練集和樣本集,用于算法的性能測試。對其數據分布情況誤差進行評分,結果如圖1所示。
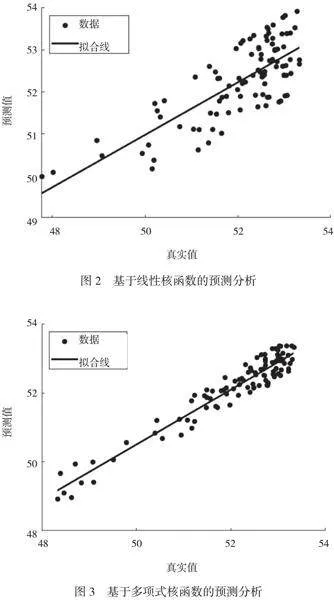
訓練樣本和測試樣本間數據差異不顯著,基于此,本文在 3 類不同核函數條件下進行分析。線性核函數的故障識別結果如圖2所示。
使用線性核函數進行支持向量回歸(SVR)時,模型的目標是在原始特征空間中找到一個線性超平面來劃分數據點,即模型試圖利用一個簡單的直線來擬合數據。由于線性核函數比較復雜,因此可能無法較好地捕捉數據中存在的潛在非線性關系。很多實際應用中的問題都包括復雜的非線性關系和模式,如果使用簡單而受限制的線性模型去逼近這些復雜結構,會導致預測結果出現較大誤差和分散現象。換句話說,在某些情況下,基于線性核函數進行預測可能會造成欠擬合問題,即使訓練集上表現良好,當遇到沒有見過的新領域、新區域時也難以準確泛化。此外,線性映射對樣本間相對位置和密度等信息處理能力有限。因此,在更抽象或者高維特征空間內部結構比較復雜的情況下,線形核函數容易失效。
多項式核函數的故障識別結果如圖3所示。多項式核函數在支持向量回歸中的作用是將數據映射到一個更高維度的特征空間,使模型可以利用多項式擬合來捕捉數據中復雜的非線性關系。與簡單的直線(一階擬合)相比,多項式核函數具有更強大和靈活的適應能力。引入高次冪和交叉項后,多項式核函數能夠表達更復雜的關系結構,并在某些情況下具有優異表現。這種方法可以幫助模型更準確地擬合訓練數據,從而對非線性關系進行建模。多項式核函數通常具有靈活、集中化和誤差率小等優勢,在特定問題領域或者數據分布下比簡單線性方法效果更好。
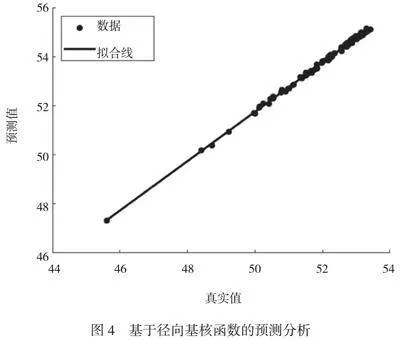
對于徑向基核函數,其故障識別結果如圖4所示。
徑向基核是一種被廣泛使用且效果優異的非參數方法,可基于輸入變量間的距離進行計算,對距離較近的數據點賦予較高的權重,對距離較遠的數據點則給予較低甚至為零的權重。這種特性使徑向基核在處理各種形狀和結構方面均表現出色,并具有較強的適應能力。根據數據點間的相對位置分配不同權重后,徑向基核可以更好地捕捉復雜、非線性關系,并有效地擬合具有不規則分布模式或者噪聲干擾的數據。
由于徑向基核具有靈活性和適應能力,因此常用于解決各類機器學習問題,特別是在涉及復雜模式識別、異常檢測以及回歸任務方面表現突出。
本文選擇基于徑向基核的SVR來執行故障預測任務,其預測形成的混淆矩陣如圖5所示。
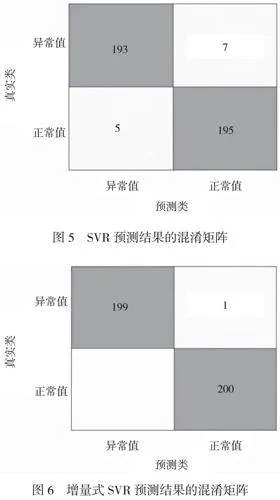
在混淆矩陣中,異常樣本有193次被成功分類為異常(True Positive),但是也有7次被錯誤分類為正常( Negative)。另外,在正常樣本方面,195次正確判定為正常(True Negative),5次被誤判為異常( Positive),可能會導致部分故障未能及時發現或者發生誤報警情況。雖然整體準確率高達96.5%,但是仍需要關注假陽性和假陰性帶來的潛在問題。
在增量式支持向量回歸(SVR)中,“異常-異常”分類實現了全數成功判斷199/200,“正常-正常”的全數200例均得以精確區分(如圖6所示),說明采用增量學習方式進行更新后,幾乎所有數據點都得到了正確的分類。從統計角度看,這種完美匹配顯示出該方法對特定任務具備較高的適應能力與有效性,能夠迅速調整自身參數并不斷提升診斷精度,對工業系統等穩固、可靠運行至關重要。
3 結語
本文建立了自動化生產線故障預警系統,利用選礦廠實際生產數據進行試驗驗證,以評估不同核函數在支持向量回歸(SVR)中的性能。結果表明,徑向基核函數在捕捉復雜非線性關系方面具有顯著優勢。根據對異常條件下的傳感器數據進行訓練和測試可知,線性核函數的簡單直線逼近限制可能無法有效應對復雜關系,而多項式核函數和徑向基核函數具有更好的擬合能力。SVR模型整體準確率為96.5%,但是存在假陽性和假陰性問題。經過增量學習后,準確率提升至99.5%,能夠有效區分故障條件,具有一定應用價值。
參考文獻
[1]陳國健,李繼庚,陳波,等.基于自編碼的長流程造紙過程斷紙故障識別[J].中國造紙,2024,43(3):113-120,141.
[2]關曉晴,衛炳坤,牛東圣,等.基于多源域數據與機器學習算法的轉子不平衡故障診斷[J].北京化工大學學報(自然科學版),2024,51(2):109-119.
[3]黃穎祺.基于機器學習的用戶側異常數據診斷研究[J].制造業自動化,2023,45(8):49-55.
[4]朱宏偉,王志文,楊波,等.基于上游單點測量信息和機器學習的氣動系統并聯雙氣缸泄漏故障診斷[J].液壓與氣動,2023,47(7):73-82.
[5]趙丹,沈志遠,宋子豪.面向不平衡數據集的礦井通風系統智能故障診斷[J].煤炭學報,2023,48(11):4112-4123.
[6]王加昌,鄭代威,唐雷,等.基于機器學習的剩余使用壽命預測實證研究[J].計算機科學,2022,49(增刊2):937-945.

