基于卡爾曼濾波的鍋爐氧量測量值融合優化方法

摘要：煙氣含氧量作為鍋爐運行的重要監控參數之一，既可反映燃燒設備與鍋爐運行的完善程度，又是確保煤粉在爐膛充分燃燒的重要依據。目前，燃煤機組多采用氧化鋯傳感器進行氧量測量，其特點是響應時間較長，測量結果隨空間位置改變，傳感器損壞時無法及時更換等。針對上述問題和難點，研究提出了一種基于卡爾曼濾波器的傳感器數據融合優化方法，并討論了該方法在DCS系統上的實現方式，使得多個測量數據的綜合結果具有更好的穩定性、抗干擾性，并可在部分設備損壞時得到可靠性更高的結果。實測數據實驗表明，卡爾曼濾波法有效改善了氧量信號的滯后性、波動性和不確定性。

關鍵詞：煙氣含氧量；卡爾曼濾波；數據融合；測量可靠性

引言

煙氣含氧量是鍋爐運行重要監控參數之一，也是反映燃燒設備與鍋爐運行完善程度的重要依據，其值的大小與鍋爐結構、燃料的種類和性質、鍋爐負荷的大小、運行配風工況等因素有關系。控制煙氣含氧量對控制燃燒過程，實現安全、高效和低污染排放十分重要。

氧量過低時，鍋爐水冷壁附近形成還原性氣氛和含量很高且對水冷壁的腐蝕非常強的H2S氣體，大幅度降低灰分在還原性氣體中的灰熔溫度，引起爐內結渣；氧量過高時，燃燒區域爐膛溫度明顯降低，無論是煤粉氣流的輻射換熱還是卷吸換熱都將減弱，煤粉氣流著火條件惡化，燃燒穩定性下降，甚至會產生鍋爐滅火的風險，低負荷下尤為突出。

合理的風煤比是提高鍋爐運行經濟性的重要措施。在一定范圍內，氧量增加，可改善煤粉與空氣的接觸和混合，有利于完全燃燒，使可燃氣體未完全燃燒熱損失和固體未完全燃燒熱損失降低。但氧量增加，鍋爐煙氣量也會隨之增加，使得排煙熱損失增大，并且增加使風機電耗。因此，對氧量測量提出了更高的要求，合理的鍋爐氧量應使各項熱損失之和為最小，鍋爐熱效率最高。

1存在問題及解決思路

鍋爐的燃燒過程涉及多個影響氧量測量的因素，包括燃料量、風量調節等。鍋爐系統中的慣性因素，如管道、閥門等，會導致信號傳輸的延遲，從而影響含氧量數據的實時性。同時，燃燒過程的復雜性使得氧量測量信號存在嚴重的噪聲干擾，包括零漂、高斯噪聲及環境因素造成傳感器自身產生的噪聲等，也會干擾測量結果。另外，鍋爐內氧氣分布還存在明顯的非均勻性。因此，通常要在多個位置及位置的多個方向設置傳感器，以獲得更可信的測量結果。

常用的氧化鋯傳感器安裝在爐膛內部，運行過程中會出現損壞卻無法維護和更換的情況，對氧量實時測量造成困擾。同時，由于氧量分布的特性及傳感器的測量方式，決定了觀測不確定性的存在，加之運行過程中也無法通過其他外部手段查看燃燒狀況和氧量情況，因此需通過算法的優化減少系統測量的不確定性。

卡爾曼濾波器是一種狀態估計算法，基本思路是綜合系統的動態模型和測量數據，以逐步優化估計狀態。其用于處理具有噪聲的測量數據，可獲得對真實狀態的最優估計，適用于燃煤電廠鍋爐氧量的測量優化。卡爾曼濾波器根據每個傳感器的實時表現，計算動態增益系數，使得多個傳感器測量結果的組合優于其中任意一個單一測量的效果；同時，由于動態增益系數，當有某個傳感器出現損壞或失靈時，優化計算結果會分配給其一個較小的權重。另外，卡爾曼增益是一個時序計算結果，當系統出現零漂等噪聲時，算法會檢測出這個偏差并向反方向調整，可有效改善系統噪聲及測量時間的滯后性、波動性。

近年來，出現了許多在燃煤電廠信號測量中使用卡爾曼濾波器獲得顯著效果的研究。如，石饒橋等[1]研究了利用卡爾曼濾波進行煙氣NOx含量測量的方法；李澤銘等[2]研究了循環流化床機組使用卡爾曼濾波進行燃料發熱量的預測；陳銳民等[3]研究了利用卡爾曼濾波器進行汽包水位的估算方法。

2卡爾曼濾波器原理與DCS實現

2.1卡爾曼濾波器的一般形式

以K-1時刻的最優估計Xk-1為準，預測K時刻的狀態變量Xk，同時又對該狀態進行觀測，得到觀測變量Zk，再在預測與觀測之間進行分析，對觀測和測量量進行修正，從而得到優化后的融合計算結果。

對于一般的氧量測量，系統測點是相互獨立非耦合的，狀態方程和協方差均為實對角陣，無控制量，觀測直接傳遞，即觀測矩陣為單位陣。

2.2氧量測量卡爾曼濾波的DCS實現

對于直接獨立的傳感器測量系統，濾波增益為每個傳感器加權結果，權重由信號的方差與實際觀測的偏差計算得到。在DCS系統中若沒有計算方差的模塊，可經過迭代計算實現。

迭代計算均值如式（5）所示。

迭代法計算的優點是可以用累加計算的方式代替寄存器，一般DCS沒有寄存器數據隊列讀取的接口，這樣計算方便使用DCS模塊實現，在測量值時間序列N足夠多的情況下，均值可用式（5）計算，均值SAMA如圖1所示。

迭代計算方差如式（6）所示，方差SAMA如圖2所示。

根據方差與偏差計算權重及濾波增益，在測量數據變化平緩的情況下也可以用如圖3所示的簡化的權重SAMA圖實現，但是測量干擾較嚴重或數據多階微分不為零的情況下偏差較大。

3數據仿真與實驗驗證

實驗采集了某300MW燃煤機組氧量采集數據。該燃煤機組使用氧化鋯氧量傳感器，其安裝位置在空預器兩側豎直煙道上，左右兩側均勻分布，共4個測點，設置卡爾曼濾波器的初始值為傳感器的初始信號值，初始迭代速率為0.1，信號采樣頻率為5min。采集的原始傳感器數據特性如表1所示。

3.1正常情況下卡爾曼濾波融合信號與單一傳感器對比

圖4為4個不同位置的氧量傳感器原始數據，每個傳感器都存在不可消除的外部噪聲與觀測噪聲，且不同位置傳感器有明顯的均值偏差。圖4中同時繪制了4個傳感器等權平均的折線與卡爾曼濾波器處理后的折線，表2列出了兩者之間均值、方差數值與偏離3σ區域的數據點個數，可見卡爾曼濾波在保證觀測可靠性的同時可以很好地消除噪聲。

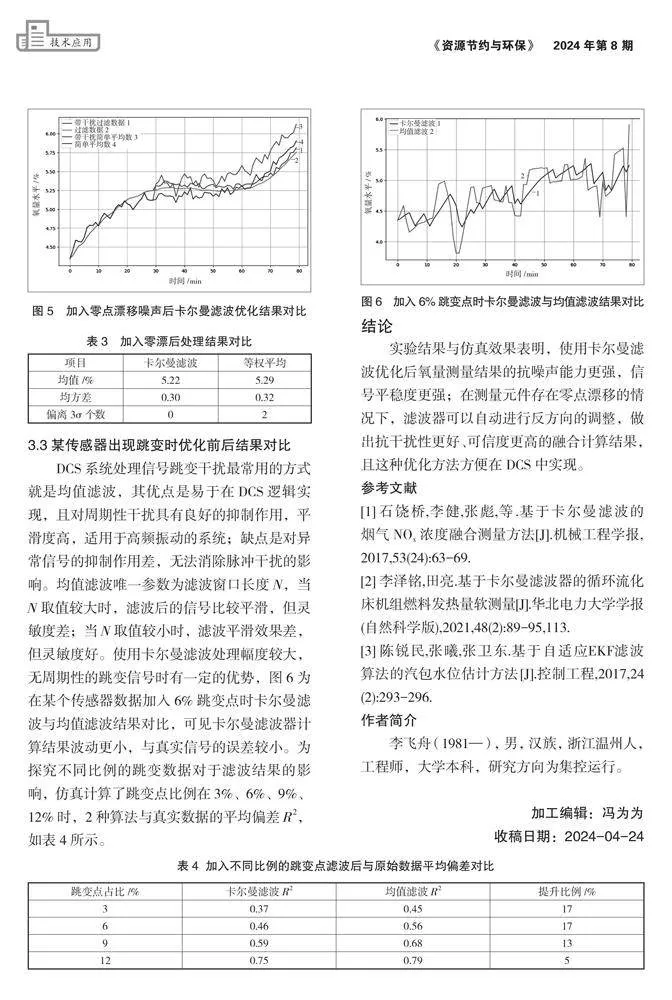
3.2某傳感器出現零漂時優化前后結果對比

圖5是在某個傳感器數據后半部分加入零點漂移干擾后2種算法的對比結果，卡爾曼濾波器會根據觀測數據，平衡測量誤差與過程誤差，降低觀測偏差大的傳感器的權重，使得最終計算結果更加可靠。加入零漂后的處理結果如表3所示。

3.3某傳感器出現跳變時優化前后結果對比

DCS系統處理信號跳變干擾最常用的方式就是均值濾波，其優點是易于在DCS邏輯實現，且對周期性干擾具有良好的抑制作用，平滑度高，適用于高頻振動的系統；缺點是對異常信號的抑制作用差，無法消除脈沖干擾的影響。均值濾波唯一參數為濾波窗口長度N，當N取值較大時，濾波后的信號比較平滑，但靈敏度差；當N取值較小時，濾波平滑效果差，但靈敏度好。使用卡爾曼濾波處理幅度較大，無周期性的跳變信號時有一定的優勢，圖6為在某個傳感器數據加入6%跳變點時卡爾曼濾波與均值濾波結果對比，可見卡爾曼濾波器計算結果波動更小，與真實信號的誤差較小。為探究不同比例的跳變數據對于濾波結果的影響，仿真計算了跳變點比例在3%、6%、9%、12%時，2種算法與真實數據的平均偏差R2，如表4所示。

結論

實驗結果與仿真效果表明，使用卡爾曼濾波優化后氧量測量結果的抗噪聲能力更強，信號平穩度更強；在測量元件存在零點漂移的情況下，濾波器可以自動進行反方向的調整，做出抗干擾性更好、可信度更高的融合計算結果，且這種優化方法方便在DCS中實現。

參考文獻

[1]石饒橋，李健，張彪，等.基于卡爾曼濾波的煙氣NOx濃度融合測量方法[J].機械工程學報，2017，53（24）：63-69.

[2]李澤銘，田亮.基于卡爾曼濾波器的循環流化床機組燃料發熱量軟測量[J].華北電力大學學報（自然科學版），2021，48（2）：89-95，113.

[3]陳銳民，張曦，張衛東.基于自適應EKF濾波算法的汽包水位估計方法[J].控制工程，2017，24（2）：293-296.

作者簡介

李飛舟（1981—），男，漢族，浙江溫州人，工程師，大學本科，研究方向為集控運行。

加工編輯：馮為為

收稿日期：2024-04-24