基于改進NSGA-Ⅱ算法的鋼箱系桿拱橋索力優(yōu)化研究

為實現(xiàn)吊桿索力的張拉方案優(yōu)化，提高系桿拱橋吊桿構件可靠性，文章提出了一種基于改進NSGA-Ⅱ算法的鋼箱系桿拱橋索力優(yōu)化模型，推導了系梁和拱肋應變能表達式，綜合系梁線形撓度偏差建立了吊桿索力優(yōu)化的雙目標函數(shù)，采用改進的NSGA-Ⅱ算法設計了吊桿索力優(yōu)化流程，并以某鋼箱系桿拱橋為工程背景，驗證了該優(yōu)化模型和優(yōu)化方法的可行性。結果表明：改進的NSGA-Ⅱ算法在求解吊桿索力優(yōu)化問題中具有良好的適應性；優(yōu)化后邊索索力存在一定下降，跨中索力得到一定的增長，整體索力較為均勻；優(yōu)化后主梁彎矩峰值降低8.59%，撓度峰值降低16.37%，提高了結構可靠性和安全冗余。

系桿拱橋；施工監(jiān)控；索力優(yōu)化；多目標優(yōu)化；NSGA-Ⅱ算法

U448.22A341194

作者簡介：

陳文華（1989—），工程師，主要從事高速公路工程項目施工質(zhì)量管理、材料物質(zhì)及機械設備管理工作。

0" 引言

系桿拱橋是兼具了拱橋與梁橋優(yōu)點，并由拱肋、系桿和吊桿三種基本構件構成的組合受力橋型。系桿拱橋結構體系中拱肋能夠承受較大的彎矩和軸力，系梁承受較大的彎矩，拱肋和系梁通過吊桿進行連接，拱肋為系梁提供豎向分力以滿足使用需求。在系桿拱橋結構體系中，吊桿作為最關鍵的傳力構件，其可靠性直接影響系桿拱橋橋梁結構體系的可靠性，因此系桿拱橋體系中吊桿的受力特性是眾多專家學者熱衷于研究的工程問題之一。

王憲玉等［1］以大跨度鋼管混凝土系桿拱橋吊桿索力為研究對象，采用能量法推導了不同約束條件下的系桿拱橋索力表達式，在優(yōu)化設計索力的基礎上對成橋和運營階段的索力展開實測分析，得到了吊桿計算抗彎剛度與實際抗彎剛度之間的異同。彭桂瀚［2］研究了吊桿布置形式對系桿拱橋結構穩(wěn)定性與動力特性的影響，對比了等間距、平行和徑向吊桿布置方式對結構地震響應特性的影響，得到了提高系桿拱橋面內(nèi)剛度的吊桿布置方式。聶尚杰等［3］以強健性為基本設計理念，通過結構計算對破斷工況下的吊桿、系桿等構件進行受力分析，并基于已有數(shù)據(jù)對結構進行優(yōu)化設計，得到了滿足強健性設計方法的大跨徑鋼管混凝土系桿拱橋結構參數(shù)，提高了結構安全冗余。齊鵬等［4］基于影響矩陣原理提出了一種特大跨徑系桿拱橋吊桿索力的優(yōu)化方法，通過實際工程驗證了該吊桿索力優(yōu)化方法在工程中的有效性，提升了系桿拱橋結構受力的合理性。高婧等［5］同樣以影響矩陣為工具建立了多跨系桿拱橋吊桿索力優(yōu)化模型，對比了6種吊桿張拉方案下的結構受力與變形，得到了保證構件應力分布均勻的吊桿張拉方案。

索力優(yōu)化問題一直以來是大跨度橋型的熱點研究問題［6-7］。從相關研究中可以發(fā)現(xiàn)，系桿拱橋中的吊桿索力優(yōu)化問題仍然依賴于比較傳統(tǒng)的優(yōu)化方法，優(yōu)化效率較低。基于此，為提高系桿拱橋吊桿索力可靠度，提升結構整體可靠性，本文以實際工程為背景，建立了一種基于改進NSGA-Ⅱ算法的鋼箱系桿拱橋索力優(yōu)化模型，相關結果可為類似研究提供一定的參考。

1" 工程背景及結構有限元模型

某下承式系桿拱橋設計全長為1 168 m，其中主橋采用預應力混凝土連續(xù)梁鋼箱拱肋組合橋，由變截面預應力混凝土連續(xù)梁主梁、拱肋、吊桿及系桿組成，跨徑布置為（80+160+80）m。橋型布置如下頁圖1所示。

為模擬鋼箱系桿拱橋空間靜力特性，采用有限元軟件建立橋梁數(shù)值計算模型，橋面系采用空間梁單元模擬，拉索采用桁架單元模擬。根據(jù)承臺基礎實際情況對承臺底面設置彈性約束，有限元模型如下頁圖2所示。

2" 考慮多目標的吊桿索力優(yōu)化模型

系桿拱橋結構內(nèi)部為多次超靜定體系［8-9］，主梁通過吊桿將梁上的大部分荷載傳遞至拱肋，在這個過程中，系桿拱橋拱肋主要以承壓為主，受彎為輔。其結構體系主要受力構件的應變能總和，如式（1）所示：

E=∫Mg（x）22EgIgdx+

∫Ng（x）22EgAgdx+

∫Mx（x）22ExIxdx+∫Nx（x）22ExAxdx（1）

式中：E——結構主要受力構件所承受的應變能總和；

Mg、Mx——拱肋、系桿承受的彎矩；

Ng、Nx——拱肋、系桿承受的軸力；

Eg、Ig、Ag——拱肋的彈性模量、截面慣性矩和截面面積；

Ex、Ix、Ax——系桿的彈性模量、截面慣性矩和截面面積。

采用有限元的方法對大跨度系桿拱橋進行數(shù)值計算時需要對結構進行離散化，根據(jù)離散單元的內(nèi)力計算結果推導任意截面的內(nèi)力值。假設離散單元兩端的截面面積與彈性模量相同，則任意離散單元截面的內(nèi)力可表示為式（2）和式（3）：

M（x）=Ml，n+Mr，n－Ml，nLn（2）

N（x）=Nl，n+Nr，n－Nl，nLn（3）

式中：M、N——單元離散后任意微分單元的彎矩、軸力；

Ml，n、Mr，n——微分單元左、右端的彎矩；

Nl，n、Nr，n——微分單元左、右端的軸力；

Ln——微分單元的單元長度。

基于改進NSGA-Ⅱ算法的鋼箱系桿拱橋索力優(yōu)化研究/陳文華

此時，離散后的結構體系應變能由各微分單元的彎曲應變能和拉壓應變能共同組成，其表達式為式（4）：" U=∑jn=1Ln6EnIn

（M2l，n+Mr，nMl，n+M2r，n）

+

∑jn=1Ln6EnAn（N2l，n+Nr，nNl，n+N2r，n）" （4）

式中：En、In和An——離散單元n的截面彈性模量、慣性矩和截面面積；

j——結構離散后的單元總數(shù)。

除結構體系應變能外，主梁線形也是大跨度系桿拱橋索力優(yōu)化的關鍵優(yōu)化目標之一，為實現(xiàn)主梁線形的精確控制，確保主梁在最不利荷載組合下不發(fā)生失穩(wěn)，定義主梁線形誤差為δ，則主梁線形誤差可表示為式（5）：

δ=1s∑si=1hi，ture－h(huán)i，target2（5）

式中：s——主梁線形標高控制點數(shù)量；

hi，ture——第i個主梁線形標高控制點的計算線形標高；

hi，target——第i個主梁線形標高控制點的設計目標標高。

綜合上述原理，建立鋼箱系桿拱橋吊桿索力優(yōu)化模型。由于結構體系呈對稱分布，以第9根吊桿為對稱軸，故取半結構吊桿索力進行尋優(yōu)，以簡化優(yōu)化問題的計算量。定義系桿拱橋吊桿索力矩陣為X=［x1，x2，…，x9］T，目標函數(shù)取由結構彎曲應變能、拉壓應變能組成的結構體系應變能和主梁線形誤差，結構體系應變能和線形誤差目標函數(shù)均取最小化，吊桿可靠度通過約束條件進行考慮，吊桿索力優(yōu)化模型目標函數(shù)如式（6）所示：

minQ（X）=min{U，δ}（6）

式中：Q（X）——系桿拱橋吊桿索力優(yōu)化目標函數(shù)。

約束條件從三個方面進行考慮：（1）基于目標函數(shù)設置約束條件，對于應變能U，將由系梁承受的彎曲應變能進行約束，防止系梁截面出現(xiàn)截面彎矩超限的情況；（2）對于主梁線形δ，約束其最大豎向撓度低于主梁撓度限值；（3）對于待優(yōu)化設計變量吊桿索力向量X，約束其相鄰索力差值在合理范圍之內(nèi)，防止相鄰索力差過大致使主梁內(nèi)力分布不合理的情況出現(xiàn)［10-11］。根據(jù)以上分析，建立吊桿索力優(yōu)化模型的約束條件如式（7）～（9）所示：

Mmin≤M≤Mmax（7）

δ≥δ0（8）

∑17i=1xi+1－xixi+12≤Δ

（9）

3" 基于改進NSGA-Ⅱ算法的吊桿索力求解方法

3.1" 改進的NSGA-Ⅱ算法

NSGA-Ⅱ算法是以遺傳算法為基本原理，在NSGA算法基礎上提出的第二代非支配排序多目標遺傳算法。NSGA-Ⅱ算法在保留了第一代非支配排序遺傳算法優(yōu)點的前提下，引入了快速非支配排序方法，大大降低了算法復雜度。本文對NSGA-Ⅱ中交叉與變異算子操作進行改進，以提升算法尋優(yōu)能力，并將其應用于考慮吊桿可靠度指標的系桿拱橋多目標索力尋優(yōu)問題。

3.1.1" 基于改進累積非支配的排序策略

在標準NSGA-Ⅱ算法中，快速非支配排序方法在一定程度上避免了多目標優(yōu)化問題中多個目標函數(shù)被加權為單適應度值進行排序的缺陷。但該非支配排序法仍然存在一定的局限性，染色體種群中密度大小不一致的個體的非支配排序值可能出現(xiàn)相同的情況，這就導致了密度不同但排序值相同的個體在進化過程中的演變概率相同，影響染色體種群的多樣性。本文引入一種基于累積排序值的非支配排序法對排序策略進行改進，假設第t代種群中染色體的個體集為qx1，qx2，…，qxn，則定義染色體x的累積非支配排序值如式（10）所示［12-14］：

r（x，t）accumulate=r（x，t）+∑ni=1r（qxi，t）（10）

式中：r（x，t）accumulate——第t代染色體個體的累積非支配排序值。

3.1.2" 動態(tài)交叉、變異算子

交叉率與變異率決定了NSGA-Ⅱ算法種群的演化策略和趨勢，交叉率越大則在每一輪進化中染色體個體參與交叉的部分更多。本文采用一種基于動態(tài)的交叉、變異算子進行染色體雜交，表達式如式（11）和式（12）所示：

Pc=（Pc1－Pc2）（favg－fa）fmax－favg，fa，max＞favg

Pc1，fa，max≤favg

（11）

Pm=（Pm1－Pm2）（favg－fa）fmax－favg，fa，max＞favg

Pm1，fa，max≤favg（12）

式中：Pc、Pm——改進NSGA-Ⅱ算法的交叉率和變異率；

Pc1、Pc2——交叉率的上、下限值，Pc1＞Pc2；

Pm1、Pm2——變異率的上、下限值，Pm1＞Pm2；

fa、fa，max——選定個體a的當前適應度與歷史最優(yōu)適應度值；

fmax、favg——種群適應度最優(yōu)值和平均值。

3.2" 基于改進NSGA-Ⅱ算法的索力求解方法

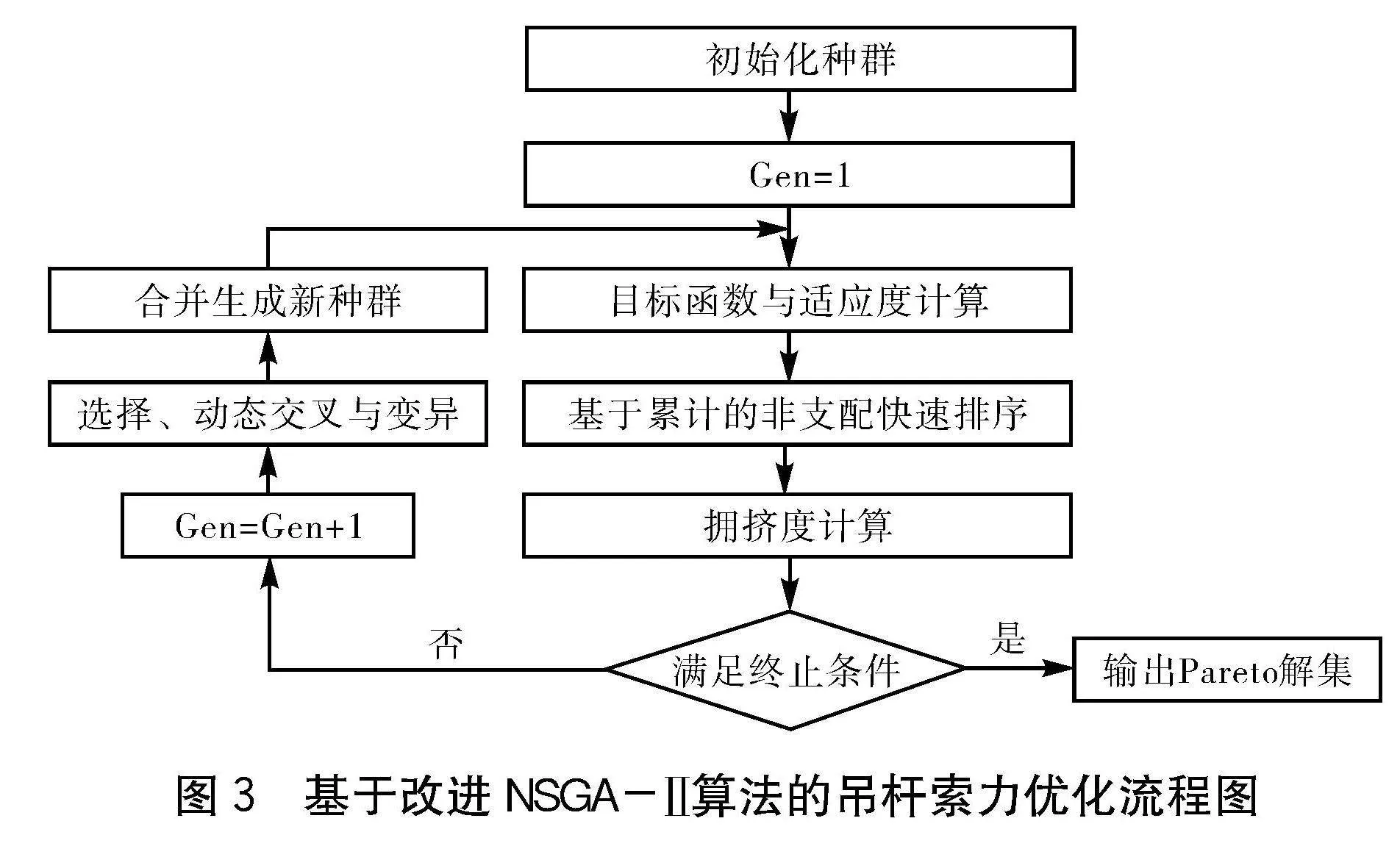
基于提出的改進NSGA-Ⅱ算法對考慮吊桿可靠度指標的系桿拱橋多目標索力優(yōu)化模型進行求解，算法編程平臺為MATLAB，求解流程設計如圖3所示。

具體步驟如下：

（1）算法初始化。初始化改進NSGA-Ⅱ算法染色體種群，設置算法基本參數(shù)，如最大進化代數(shù)、交叉率上下限值、變異率上下限值等信息。

（2）目標函數(shù)適應度計算。通過MATLAB軟件與有限元平臺進行數(shù)據(jù)交互，基于有限元數(shù)值模型計算目標

函數(shù)值，得到系桿拱橋結構體系應變能、主梁線形撓度數(shù)據(jù)，返回MATLAB軟件的改進NSGA-Ⅱ算法中作為種群適應度指標，判別個體優(yōu)劣程度。

（3）非支配排序與擁擠度計算。基于累積排序值原理對種群進行快速非支配排序，并對非支配個體計算擁擠度，根據(jù)種群擁擠度信息生成新的父代種群。

（4）交叉與變異。基于動態(tài)交叉、變異原理計算當前進化代次的交叉率和變異率值，基于新的父代種群采取交叉、變異操作，生成新的子代種群，并與有限元軟件進行數(shù)據(jù)交互，計算子代種群的目標函數(shù)值與適應度信息。

（5）終止條件判斷。判斷種群是否滿足設置的最大進化代數(shù)，若滿足則算法進程終止，輸出Pareto解集并解碼得到符合目標函數(shù)設計的吊桿索力組合，若不滿足則重復步驟（3）和步驟（4）。

4" 優(yōu)化結果分析

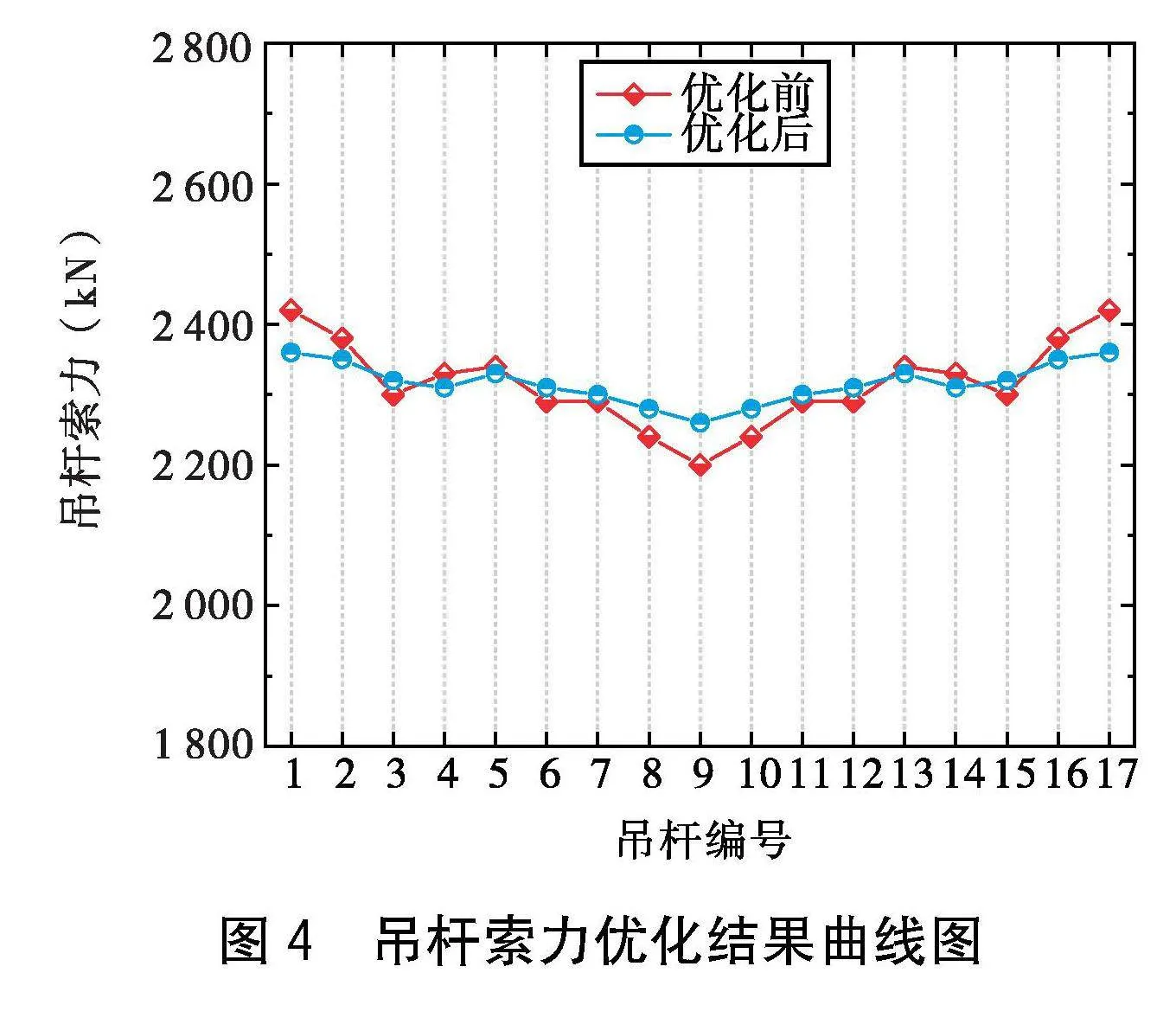
基于MATLAB軟件編寫優(yōu)化程序，改進NSGA-Ⅱ算法相關參數(shù)如下：種群規(guī)模為30，最大進化代數(shù)為200，Pc1=0.9，Pc2=0.4，Pm1=0.1，Pm2=0.004，取兼顧結構體系應變能和主梁線形撓度偏差兩個目標函數(shù)的候選方案進行分析。如圖4所示給出了設計索力與優(yōu)化索力的分布結果。由圖4可知，優(yōu)化后邊索1#、2#和16#、17#索力出現(xiàn)明顯降低，其中1#和17#號吊桿索力由2 420 kN降低至2 360 kN，降幅達2.48%。中索8#、9#、10#相較于優(yōu)化前顯著提升，其中跨中9#吊桿索力由2 200 kN提升至2 260 kN，最大增幅約2.73%。其余各索與優(yōu)化前差異較小，相對變化量＜1%。由于約束條件中考慮了相鄰索力之間的均勻度限制，吊桿索力極差由220 kN降低至102 kN，吊桿索力整體均勻度得到改善。

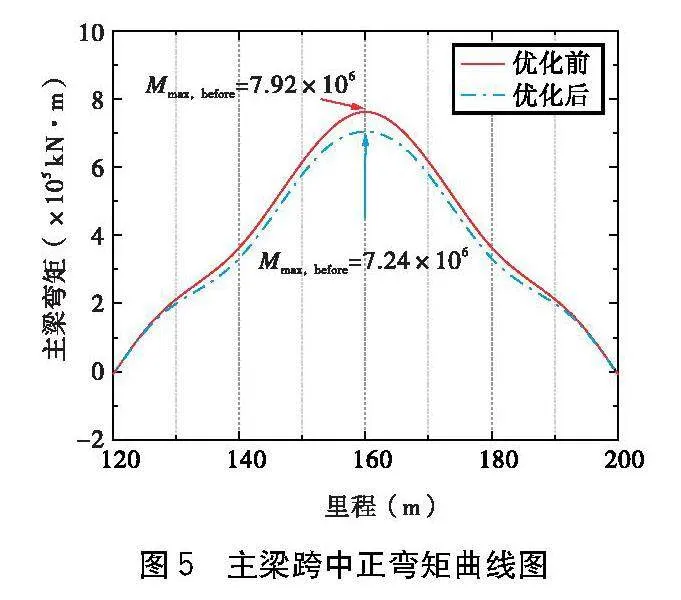
如圖5所示給出了主梁跨中關鍵截面的彎矩分布曲線。由圖5可知，越靠近橋墩側主梁正彎矩越小，且差異較小，越靠近跨中部位主梁正彎矩越大，且主梁彎矩降幅越大。優(yōu)化前主梁跨中截面最大正彎矩為7.92×106 kN·m，優(yōu)化后該截面峰值彎矩降至7.24×106 kN·m，最大降幅約為8.59%，說明優(yōu)化后的吊桿索力在一定程度上降低了主梁在恒載下的彎矩，提升了主梁承受活載效應的能力。

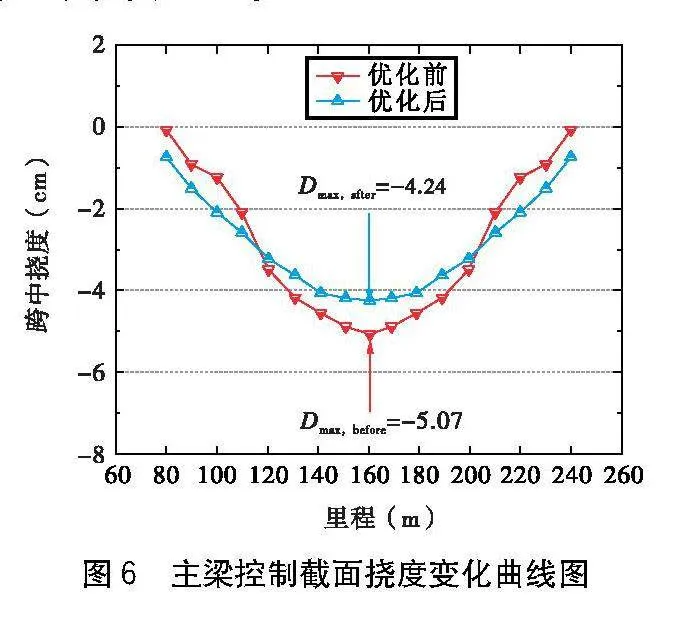
如圖6所示給出了主梁部分截面的撓度變化曲線。由圖6可知，由于邊索索力的降低，優(yōu)化后80～100 m、220～240 m的部分截面主梁撓度相較于優(yōu)化前存在一定的增大。主梁跨中撓度峰值由5.07 cm減小至4.24 cm，最大降幅約為16.37%。優(yōu)化后主梁線形撓度明顯改善，提高了結構安全冗余。

5" 結語

本文針對鋼箱系桿拱橋的吊桿索力優(yōu)化問題，提出了一種考慮吊桿索力可靠度指標的索力優(yōu)化方法。綜合考慮結構體系應變能以及主梁線形建立了系桿拱橋吊桿索力多目標優(yōu)化模型，將吊桿索力可靠度指標轉化為模型約束條件，采用改進的NSGA-Ⅱ算法對考慮可靠度指標約束的多目標索力優(yōu)化問題進行求解，得到結論如下：

（1）建立了考慮吊桿索力可靠度指標的系桿拱橋吊桿索力優(yōu)化模型，以結構體系應變能和主梁線形撓度為目標函數(shù)，吊桿可靠度指標為約束條件，實現(xiàn)了系桿拱橋的吊桿索力優(yōu)化。

（2）優(yōu)化后結構邊索索力有所降低，1#、17#號索降幅約為2.48%，跨中8#～10#號索力明顯增長，其中9#號中索的索力由2 200 kN提升至2 260 kN，增幅約為2.73%。優(yōu)化后索力平均可靠度指標由3.906增長至4.010，降低了結構索力失效概率。

（3）優(yōu)化后結構主梁跨中彎矩峰值由7.92×106 kN·m降低至7.24×106 kN·m，降幅約為8.59%。主梁跨中撓度峰值由5.07 cm減小至4.24 cm，降幅約為16.37%。優(yōu)化前后的結構響應表明，考慮可靠度指標的系桿拱橋吊桿索力優(yōu)化模型在一定程度上改善了結構內(nèi)力與變形，同時提高了吊桿可靠性，可為類似工程提供一定的參考。

［1］王憲玉，王興武，梁" 孝，等.大跨度鋼管混凝土系桿拱橋吊桿索力分析［J］.振動與沖擊，2023，42（17）：306-313.

［2］彭桂瀚.鋼管混凝土系桿拱橋吊桿布置形式對結構穩(wěn)定與動力性能的影響［J］.公路工程，2010，35（4）：31-36.

［3］聶尚杰，王鋮鋮，劉" 琪，等.基于強健性的大跨徑鋼管混凝土剛架系桿拱橋設計［J］.橋梁建設，2023，53（S1）：91-97.

［4］齊" 鵬，魏海龍，孫鎮(zhèn)國，等.特大跨徑拱橋系桿張拉優(yōu)化方法研究［J］.公路交通科技，2023，40（5）：85-91，99.

［5］高" 婧，陳龍云，王俊文.基于影響矩陣法的多跨系桿拱橋吊桿張拉力計算與優(yōu)化［J］.公路，2022，67（9）：165-170.

［6］付慧建，鄧超騫，孫" 傲，等.基于Kriging-ISOA的大跨度RC拱橋施工階段扣索索力優(yōu)化研究［J］.公路工程，2023，48（3）：18-25.

［7］覃木寶，王" 華，王龍林.基于改進海鷗算法優(yōu)化支持向量機的斜拉橋索力優(yōu)化研究［J］.森林工程，2023，39（4）：160-169.

［8］文啟軍，李" 杰，吳" 欣，等.基于優(yōu)化Kriging模型的小概率失效結構可靠度計算方法［J］.公路工程，2023，48（4）：37-43，90.

［9］徐海賓，雷余鵬，李" 磊.桁式鋼管混凝土系桿拱橋拱軸線及吊桿索力優(yōu)化［J］.科學技術與工程，2023，23（22）：9 659-9 665.

［10］陳" 干，陳明芳，陳常松.基于改進ACO-SVM的斜拉橋可靠度及參數(shù)敏感性分析［J］.公路工程，2023，48（3）：26-33，96.

［11］楊雅勛，張宇航，柴文浩，等.改進粒子群算法在系桿拱橋成橋索力優(yōu)化中的應用［J］.武漢大學學報（工學版），2022，55（6）：589-595.

［12］鄭" 夏，馬" 良.一種多目標非線性優(yōu)化的NSGA-Ⅱ改進算法［J］.微電子學與計算機，2020，37（7）：47-53.

［13］Shinya Honda，Teruki Igarashi，Yoshihiro Narita.Multi-objective optimization of curvilinear fiber shapes for laminated composite plates by using NSGA-Ⅱ［J］.Composites Part B，2013（1）：1 071-1 078.

［14］Dexuan Zou，Haikuan Liu，Liqun Gao，et al.An improved differential evolution algorithm for the task assignment problem［J］.Engineering Applications of Artificial Intelligence，2011（4）：616-424.

20240312