基于博弈論組合賦權模糊數學的地質環境復雜性研究

摘" 要：隨著人類改造自然能力的提高，地質環境發生巨大變化，與地質環境承載力、地質災害風險評價相比，地質環境復雜性評價指標涵蓋面更廣，復雜程度的高低影響著許多工程的開展及規范政策的制定。基于此，該文采用主觀權重、客觀權重、博弈論組合權重分別賦權模糊數學模型，選取單點降雨、活動構造、人文活動和工程活動等16個指標為評價指標，對代表性較強的紅河、鎮雄、勐臘地區進行地質環境復雜性評價。結果發現，云南特有的大面積礦山開采活動、豐富的少數民族人文活動對單一賦權評價結果具有一定的影響，博弈論賦權模糊數學模型具有較為精確的評價結果，且高原山區地質環境復雜性差別較大，可將該評價方法進行推廣，進而制定各地區工程、人文等活動的相關規范及政策。

關鍵詞：博弈論；組合權重；模糊數學；地質環境；復雜性

中圖分類號：P624 文獻標志碼：A 文章編號：2095-2945（2025）04-0015-06

Abstract： With the increase of human ability to transform nature， the geological environment has undergone tremendous changes. Compared with the geological environment carrying capacity and geological disaster risk assessment， the geological environment complexity assessment indicators cover a wider range， and the level of complexity affects the development of many projects and the formulation of standardized policies. Based on this， this paper uses subjective weight， objective weight， and Game Theory combination weighting to weight fuzzy mathematical models respectively， and selects 16 indicators such as single point rainfall， active structures， cultural activities， and engineering activities as evaluation indicators to evaluate the geological environment complexity in Honghe， Zhenxiong and Mengla areas， which are highly representative. The results show that Yunnan's unique large-area mining activities and rich cultural activities of ethnic minorities have a certain impact on the single empowerment evaluation result. The Game Theory weighted fuzzy mathematical model has relatively accurate evaluation results， and the complexity of geological environments in plateau and mountainous areas varies greatly. This evaluation method can be promoted and relevant norms and policies for engineering， cultural and other activities in various regions can be formulated.

Keywords： Game Theory; combination weighting; fuzzy mathematics; geological environment; complexity

地質環境是自然環境的一部分，是國土空間規劃的重要依據，為人類提供了生存空間和資源，隨著人類改造自然的能力不斷提高，地質環境的復雜程度也在發生變化，科學的地質環境復雜性評價對人類活動的開展尤為重要。目前，針對地質環境以及風險性的評價已有較多學者進行研究。匡恒等[1]建立數學模型對開封地區的地質環境危險性和社會經濟易損性進行評價，并取得了較好效果，在此基礎上提出了合理的功能優化和風險防控措施；Yang等[2]考慮地基穩定性、地下水和排水條件等多方面因素建立模糊數學模型對地質環境條件進行評價，并將單因素和多因素評價進行綜合對比分析，得出多因素對地質條件評價具有高的適用性；孟暉等[3]建立差異化評價指標對全國地質環境承載能力進行評價，并根據評價結果對全國大部分地區的地質環境承載能力進行分區；謝紀強等[4]利用極差最大化組合賦權法對伊利地區水環境進行評價，并將該方法運用于地區的水資源管理；張以晨等[5]構建風險評價體系對地質災害風險等級進行劃分，結果發現評價結果與實際風險等級相吻合；Siles等[6]采用多時相干涉測量技術評估了墨西哥北部地區的變形過程，對地質災害評價提供了有力的依據。然而，在現有研究中采用的賦權方法存在賦權方法單一和多種權重組合不合理的問題，針對這一缺陷，路遙等[7]采用博弈論賦權法進行組合賦權，在主觀和客觀權重之間尋求最優解，通過對泥石流災害等級評價發現采用該方法賦權可取得較好的評價結果；陽雨平等[8-13]將博弈論組合賦權運用到施工、防洪、礦山以及電力等多個領域，均取得較好效果。

綜上所述，博弈論可將權重賦值更加科學，但上述研究多是針對地質災害、環境承載力等地質方面進行研究，然而2016年全國科學技術名詞審定委員會首次將環境的復雜性列入管理科學技術名詞，而地質環境復雜性是環境復雜性的重要組成部分，對其研究較少。基于此，本文選取地質環境代表性較強的云南高原山區，以云南紅河、鎮雄、勐臘為依托，利用博弈論組合賦權模糊數學模型對該地區的地質環境復雜性進行評價，通過與實際復雜程度進行對比，驗證該方法的適用性。

1" 博弈論組合權重的確定

1.1" 主觀權重的確定

主觀權重其性質為根據決策者的經驗來判斷某一指標的權重，主要有AHP（層次分析法）、Delphi（專家調查法）等，與其他方法相比，AHP具有可將評估過程簡化、彌補資料不足等優點，所以該方法被廣泛運用于各行業評價的權重確定[14]。但因AHP法中九標度法的主觀性較強，同時在實際應用中往往因反復多次地進行一致性檢驗而使計算過程較為繁瑣，因此，學者開始使用三標度層次分析法進行權重確定[15]，具體計算步驟如下。

1.1.1" 構造判斷矩陣Q

Q=（qu）m×n ，" "（1）

式中：若第u個指標更重要，則qu=1；若第u與個指標一樣重要，則qu=０；若第個指標更重要，取qu=－1。

1.1.2nbsp; 計算最優傳遞矩陣B及一致性判斷矩陣C

傳遞矩陣B中的元素bu=quk+qk，C中的元素cuv=exp（buv）。

1.1.3" 計算C的特征向量

先計算矩陣C中每一行元素的積Pu=cu，然后計算=，并對向量=[，，…，]Ｔ進行歸一化處理，從而得到相應的特征向量=[1，2，…，z]Ｔ，即代表各指標的權重系數。

1.2" 客觀權重的確定

客觀權重主要根據數據間的聯系，使用數學方法來計算確定，其判斷結果不依賴于人的主觀判斷，有較強的數學理論依據，主要有主成分分析法、離差及均方差法、熵值法等。其中熵值法根據各項指標指的變異程度來確定指標權數的，能夠更好的解釋所得結果[16]，假設有m個待測樣本，n個評價指標，則原始數據的矩陣為Xij=（xij）m×n，Xij越大，在綜合評價中這個指標比重越大，對數據進行標準化及歸一化處理后，可采用如下步驟進行權重計算。

1.2.1" 數據處理

根據選取的指標進行有關數據的提取，形成原始數據矩陣，進行指標的標準化處理其處理公式為

，" " （2）

式中： 為標準化后的指標值； 為指標原始值；xj為第j各指標的平均值；Sj為第j個指標的標準差。

1.2.2" 數據的歸一化處理

根據指標對地質環境的作用方向，可以將其劃分為正效指標和負效指標。正效指標的值越大，地質環境質量越好；負效指標反之。歸一化公式如下

1.2.3" 計算第j項指標下第i方案指標值的權重pij

1.2.4" 計算第j項指標的熵值ej

式中：k＞0，ej≥0。

如果xij對于給定的j全部相等，那么

此時ej取極大值，即

若設k=1/ln m，則0≤ej≤1。

1.2.5" 差異性系數計算

對于給定的j，xij的差異性越小，則ej越大，指標就越重要，當xij全部相等時，ej=1，此時對于方案的比較，指標xij毫無作用，當方案的指標值相差越大，ej越小，該項指標對方案比較所起的作用越大。定義差異性系數為

gj=1-ej 。 （9）

1.2.6" 指標定權

第j項指標的權重

1.3" 博弈論組合權重的確定

AHP和熵值法分別為主客觀賦權使用較為廣泛的方法，但2種方法所得權重往往有較大的差別，因此學者開始將主客觀權重相結合對評價指標進行賦權，如理想點法、拉格朗日算法、博弈論等。其中博弈論可以在不同評價方法之間尋找一致性，通過2種或多種方法的相互比較妥協獲得主觀權重[7]，從而達到組合權重與各個權重的偏差達到最小化，組合賦權過程如下。

1.3.1" 確定基本權重向量集

假設共有k種方法賦權方法對地質環境復雜性進行了評價，則可得到k種權重向量。

， （11）

式中：i為第i中方法確定的權重。

則k種權重向量的任意線性組合為

式中：q為線性組合系數，為k種權重集中的一種綜合權重值。

1.3.2" 確定最組合權重

根據博弈論的基本思想，確定最優組合權重的過程即為各權重之間的博弈，從而尋找最優組合達到各權重之間的一致或妥協。這一過程可轉化為對線性組合系數 的優化，從而使組合權重與各個權重i之間的離差達到最小值，該過程表達式如下

根據矩陣的微分性質可知，當式（13）達到最優化時，滿足下式要求

式（14）對應的線性方程組為

由式（15）可得線性組合系數（1，2，…，k），歸一化后可得，將其代入式（12），即可求得最優組合權重。即

1.4" 博弈論組合賦權的模糊數學評價模型

模糊數學評價模型共有6個基本要素組成，其中包括因素集U、評判級V、模糊關系矩陣R、指標權重、合成因子？茚和結果向量B。假設評價對象有m個評價指標、n個評價等級，則可構造因素集U={u1，u2，…，un}和評判集V={1，2，…，n}；若對U中每個因素做一個評判，則可得到U到V的一個模糊映射f，該映射的模糊關系為Rf∈F（Ｕ×Ｖ），進而求出模糊關系矩陣R，即

，（17）

式中：rij為第i個評價指標隸屬于第j個等級的程度，又稱為單指標隸屬度，數值在0～1之間，由隸屬函數確定。隸屬函數由多種表達式，最后計算結果相同，所以一般按照評價指標的具體情況選擇便于計算的隸屬函數，因此，本文采用三角形隸屬函數式（19）確定每個指標的隸屬度

根據上述所求博弈論組合權重，利用合成因子對評價對象進行模糊運算，即可得出最終評價結果

2" 高原山區地質環境復雜性評價

2.1" 云南高原山區概況

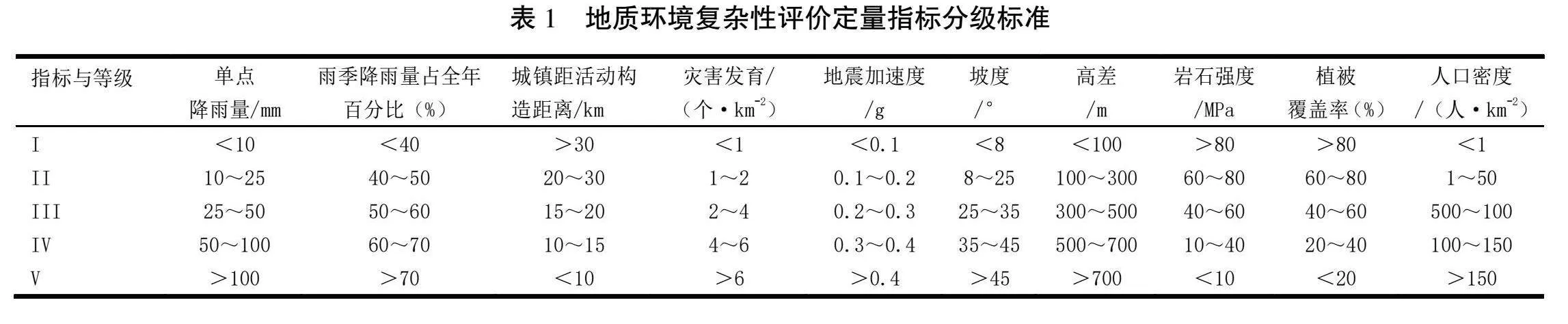
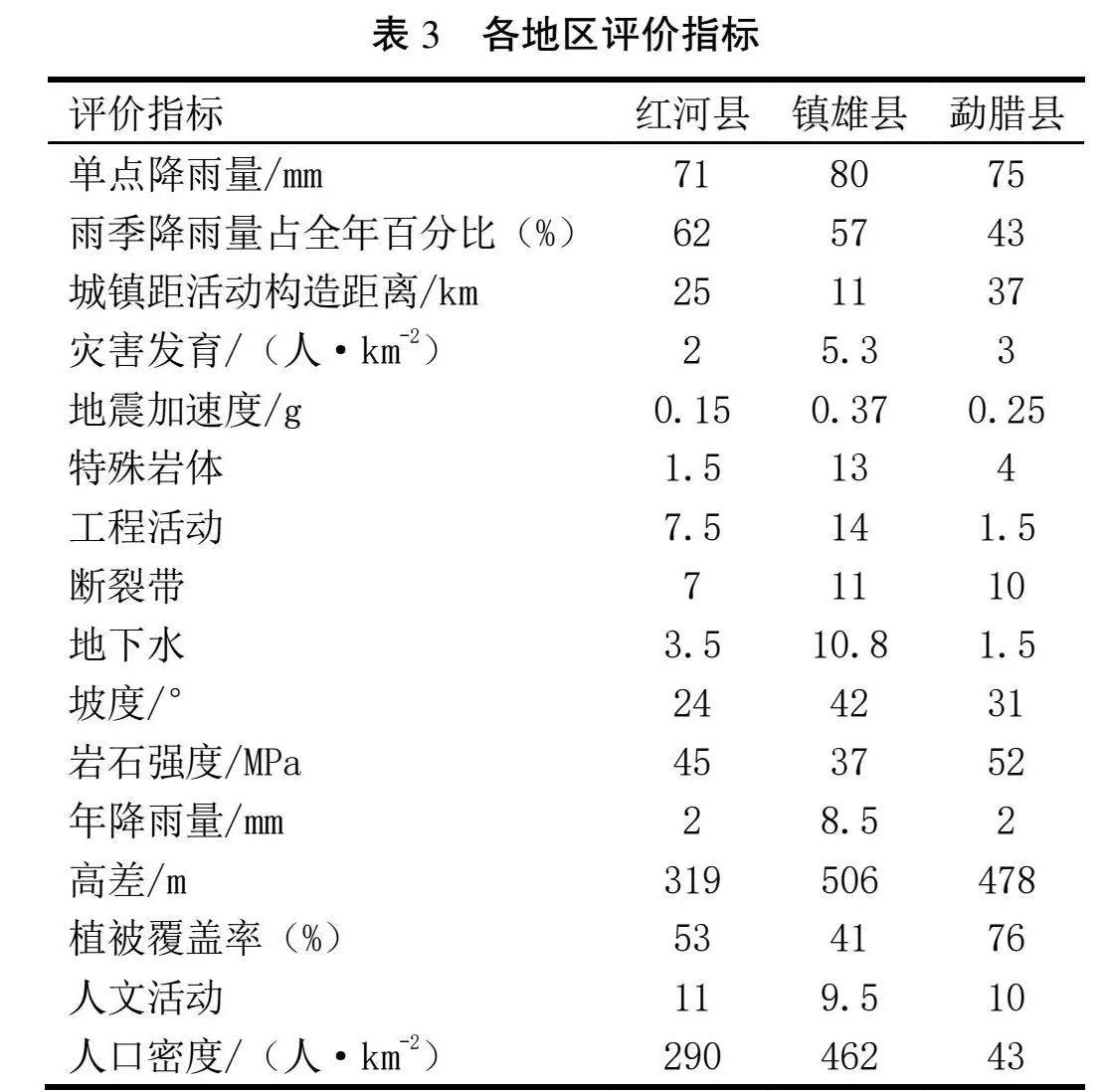
與地質環境承載能力、地質災害風險性評等地質評價不同，地質環境復雜性評價是對整個環境的綜合性評價，包含自然條件、地質構造、水文條件、人文和工程活動等多方面指標，結合專家建議與評價地區實際狀況，本文選取單點降雨、雨季占比、活動構造等16個評價指標對紅河、鎮雄、勐臘3個代表性較強的地區進行復雜性評價，評價指標分級標準及評價對象指標值見表1—表3。

2.2" 基于博弈論的組合權重確定

以紅河縣為例，根據章節1.1—1.3介紹內容，可分別求出主觀權重ω1、客觀權重ω2和組合權重ω具體如下。

構造判斷矩陣Q、最優傳遞矩陣B和一致性判斷矩陣C（只列舉Q）

將C中每行元素的乘積開16次方即可得到各指標主觀權重

。（22）

以集中降雨為例，可根據隸屬函數求出指標在各等級所占權重為" " nbsp; " " " " " " " "，將pij代入式（6）—式（10）即可求得各指標客觀權重

。（23）

根據博弈論的思想，組合權重即為多種權重為尋求最優解的博弈，將1和2代入式（14）求出1、2

將1、2代入式（15）即可求出最優組合權重

。（25）

2.3" 高原山區地質環境復雜性評價

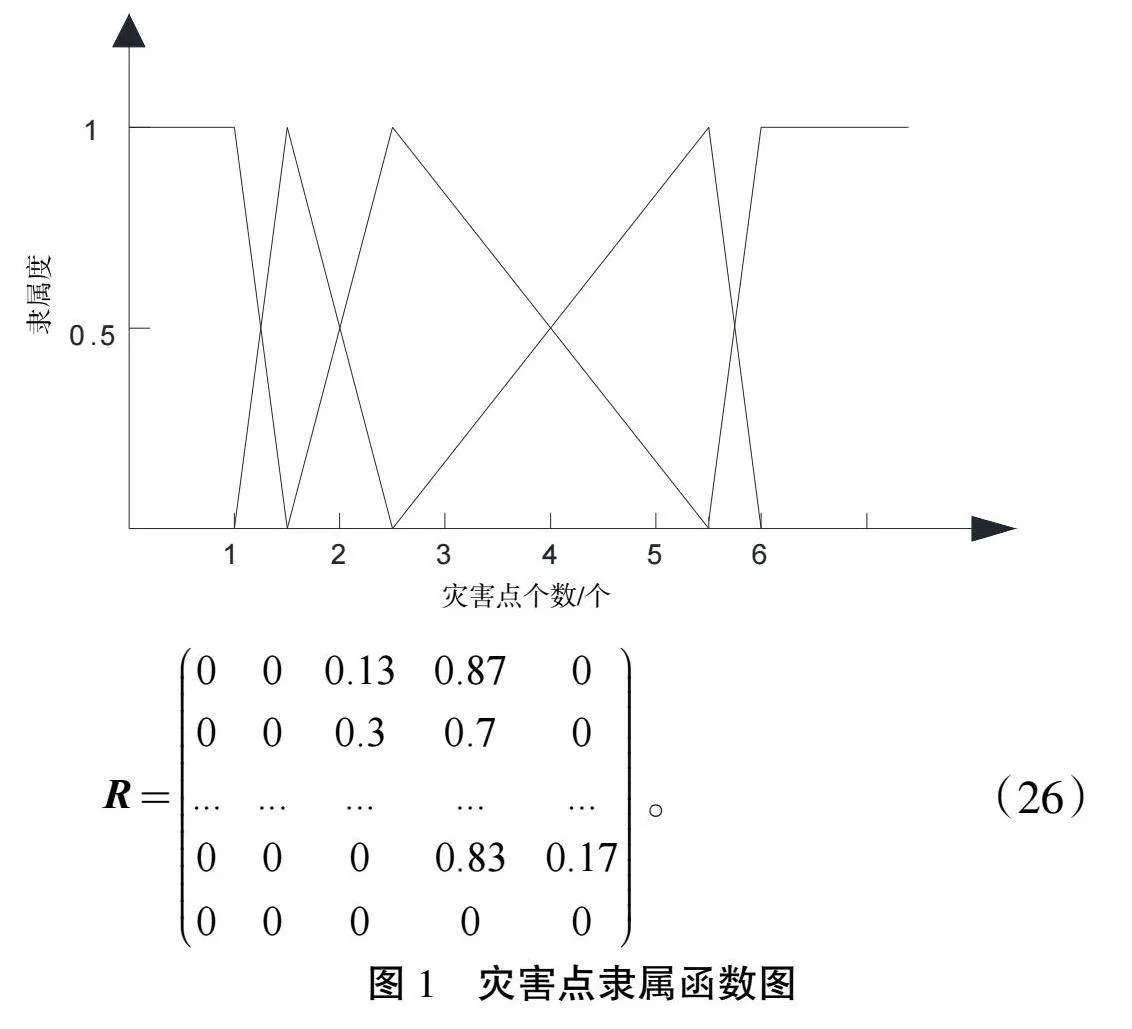
結合各地區評價，利用式（19）可繪制隸屬曲線如圖1（災害點個數為例）所示，進而求出指標與隸屬函數，可構造模糊矩陣R（以紅河縣為例）。

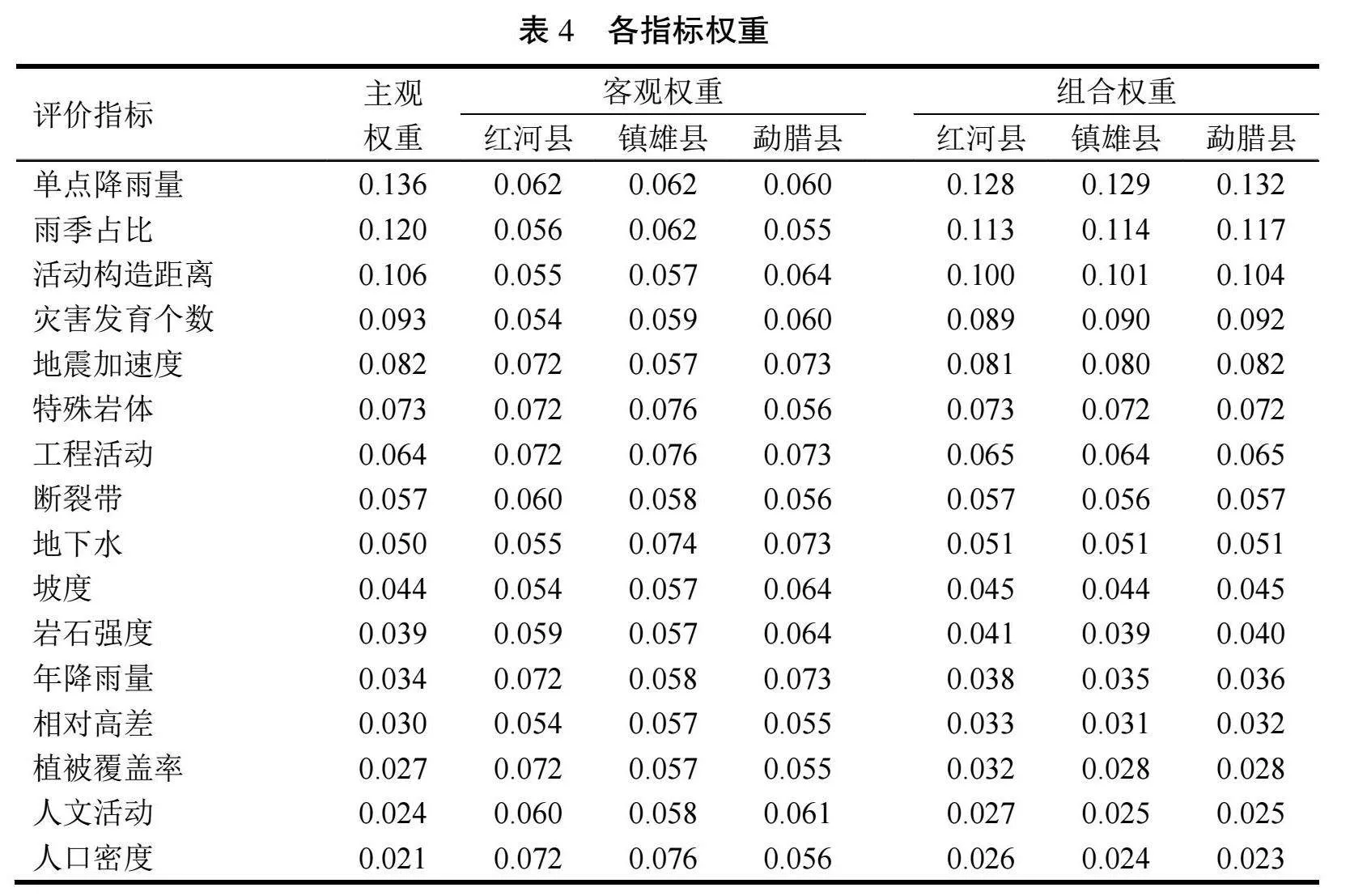
根據模糊評價原則，將指標權重與模糊矩陣相乘即可得出最終評價結果，為驗證該方法的準確性，本文將主觀權重、客觀權重和組合權重分與模糊矩陣相乘，各指標權重見表4，得出3個地區地質環境復雜性評價結果，見表5。

由表4可知，主觀權重和客觀權重在對高原山區地質環境復雜性評價時會出現一定的偏差，偏差主要由以下原因造成：①云南處于高原山區，且礦產資源豐富，以鎮雄縣為例，鎮雄縣高原、山地面積約占全域80%，且山地內多數礦產資源正在被開采，因此在進行賦權時考慮開采情況，主觀權重往往較大；②云南是少數民族聚集區，以紅河縣為例，縣內哈尼族、彝族、瑤族等少數民族占總人口的94%，這就造成少數民族文化及人文活動極為豐富，該指標權重往往較大，但該活動對地質環境影響較小，所以或造成客觀權重評價等級偏小。基于此，運用博弈論的思想來確定組合權重可以彌補單一賦權方式的缺陷，該方法可根據主客觀權重之間的差異進行比較妥協，從而卻行最優權重，因此，該方法在高原山區地質環境復雜性評價具有較好的適用性。

3" 結論

1）云南地處高原山區，地質環境復雜性評價需要自然環境、人文活動、水文條件和工程活動等多方面指標，與地質環境承載力、地質災害易發性等評價相比，環境復雜性評價考慮更加全面；建立起合理的復雜性評價指標對開展地質相關工作具有重要意義。

2）通過主觀權重、客觀權重和基于博弈論的組合權重分別賦權模糊數學模型對比發現，云南特有的礦山開采活動、少人民族人文活動對單一賦權評價結果具有一定的影響，博弈論組合權重評價結果更加合理，該方法可作為高原山區地質環境復雜性評價的重要方法進行推廣。

3）選取紅河、鎮雄、勐臘3個具有代表性的地區進行評價，發現各地區評價結果和評價指標具有較大差別。因此，對高原山區各區域進行復雜性評價，并根據評價結果建立起不同的人文、工程等活動的相關規定尤為重要。

參考文獻：

[1] 匡恒，馬傳明，和澤康.基于城市規劃的開封市地質環境風險評價[J].環境工程，2016，34（2）：133-137，132.

[2] YANG Ｎ， ＷＡＮＧ Ｃ， FU Y. Research on construction of industrial environment system of cross-border e-commerce in free trade zone based on geological environment assessment method[C]//IOP Conference Series： Earth and Environmental Science. IOP Publishinｇ，２０２１，６３２（２）： ０２２０３１．

[3] 孟暉，李春燕，張若琳，等.全國地質環境承載能力評價[J].地質通報，2021，40（4）：451-459.

[4] 謝紀強，游進軍，姜紀沂.基于級差最大化組合賦權法的淺層地下水功能評價[J].水資源保護，2021，37（6）：54-59.

[5] 張以晨，郎秋玲，陳亞南，等.基于自然災害風險評價框架的省級地質災害風險區劃方法探討——以吉林省為例[J].中國地質災害與防治學報，2020，31（6）：104-110.

[6] SILES Ｇ， ＪＵＡＮ Ａ， ＰＥＮ？魪ＬＯＰＥ Ｌ， ｅｔ ａｌ． Ｌｏｎｇ Ｔｅｒｍ Ｓｕｂｓｉｄｅｎｃｅ Ａｎａｌｙｓｉｓ ａｎｄ Ｓｏｉｌ Ｆｒａｃｔｕｒｉｎｇ Zonation Based on InSAR Time Series Modelling in Northern Zona Metropolitana del Valle de Mexico[J].Remoｔｅ Ｓｅｎｓｉｎｇ，２０１５.

[7] 路遙，徐林榮，陳舒陽，等.基于博弈論組合賦權的泥石流危險度評價[J].災害學，2014，29（1）：194-200.

[8] 陽雨平，陳國國，楊田杰，等.基于博弈論組合賦權的湘南某礦凈化庫防洪風險評價云模型研究[J].安全與環境學報，2021，21（2）：546-553.

[9] LIU Ｂ， ＬＩ Ｊ， ＺＨＥＮＧ Ｓ. Competitiveness evaluation of pharmaceutical logistics centres based on combined weight and cumulative prospect theory[J].IOP Coｎｆｅｒｅｎｃｅ Ｓｅｒｉｅｓ Ｅａｒｔｈ ａｎｄ Ｅｎｖｉｒｏｎｍｅｎｔａｌ Ｓｃｉｅｎｃｅ，２０１９．

[10] ZHU Ｄ， ＷＡＮＧ Ｒ， ＤＵＡＮ Ｊ， ｅｔ ａｌ． Comprehensive weight method based on game theory for identify critical transmission lines in power system[J].International Journal of Electrical Power amp; Energy Ｓｙｓｔｅｍｓ，２０２１（１２４）：１０６３６２．

[11] 景耀斌，顧偉紅，翟強.基于博弈論組合賦權的水工隧洞TBM施工地質適宜性評價模型[J].安全與環境工程，2021，28（2）：95-101，108.

[12] 趙浩楊，石廣斌，楊振宏，等.基于組合賦權-改進集對分析的巖爆傾向性預測研究[J].金屬礦山，2021（5）：71-77.

[13] XIAO L W， ＧＡＯ Ｘ Ｗ， ＹＯＮＧ Ｘ Ｗ， ｅｔ ａｌ． Ｃｏｍｐｒｅｈｅｎｓｉｖｅ ａｓｓｅｓｓｍｅｎｔ ｏｆ ｒｅｇｉｏnal water usage efficiency control based on game theory weight and a Matter-Element Model[J].Ｗａｔｅｒ，２０１７，９（２）：１１３．

[14] KARAYALCIN I I. The analytic hierarchy proceｓｓ：Planning， priority setｔｉｎｇ，ｒｅｓｏｕｒｃｅ ａｌｌｏｃａｔｉｏｎ：Ｔhomas L. SAATY McGraw－Ｈｉｌｌ，Ｎｅｗ Ｙｏｒｋ，１９８０，ｘｉｉｉ＋２８７ｐａｇｅｓ，15.65[J].European Journaｌ ｏｆ Ｏｐｅｒａｔｉｏｎａｌ Ｒｅｓｅａｒｃｈ，１９８２，９（１）：９７－98.

[15] 阮永芬，陳趙慧，吳龍，等.基于可拓云理論的泥炭質土場地沉降風險評價[J].安全與環境學報，2020，20（1）：59-67.

[16] BAAKE Ｐ， BOOM A. Vertical Product Differentiation， Network Externaliｔｉｅｓ，ａnd Compatibility Decisions[J].International Journal of Industrial Organizatioｎ，２００１，１９（１－２）：２６７－２８４．