主元法在求解競賽題中的運用

陳志恩

(浙江省永康市教師進修學校附屬初中,321300)

對于含有多個變量或含有參數(shù)的數(shù)學問題,若以題設或習慣中的主要變量解決問題比較困難時,我們可根據(jù)題意條件視其他變量為“主元”,或合理使用參數(shù),將參數(shù)與變量身份互換,從而降低解題難度,使問題迎刃而解.這一解決問題的方法我們稱之為“主元法”.本文以相關數(shù)學競賽試題為例,說明“主元法”在解題中的運用.

一、求解多位數(shù)

例1(2003年全國初中數(shù)學聯(lián)賽第二試試題)試求出這樣的四位數(shù),它的前兩位數(shù)字與后兩位數(shù)字分別組成的二位數(shù)之和的平方,恰好等于這個四位數(shù).

解析設前后兩個二位數(shù)分別為x,y,10≤x,y≤99,則有(x+y)2=100x+y,

∴x2+2(y-50)x+(y2-y)=0.

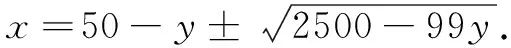
由于2500-99y必為完全平方數(shù),而完全平方數(shù)的末位數(shù)字僅可能為0,1,4,5,6,9,故y僅可取25,此時x=30或x=20.

故所求的四位數(shù)為2025或3025.

點評本題設出的兩個變量x,y地位相同,但為了解題需要,我們視x為“主元”,y為常量,將方程整理成關于x的一元二次方程來求解的.

二、因式分解

例2(第21屆“希望杯”全國數(shù)學邀請賽初二第二試試題)將代數(shù)式x3+(2a+1)x2+(a2+2a-1)x+(a2-1)分解因式,得______.

解析視a為“主元”，得

x3+(2a+1)x2+(a2+2a-1)x+(a2-1)=(x+1)a2+(2x2+2x)a+x3+x2-x-1=(x+1)a2+2x(x+1)a+x2(x+1)-(x+1)=(x+1)(a2+2xa+x2-1)=(x+1)(x+a+1)(x+a-1).

點評在分解含有多個字母的代數(shù)式時,視其中一個字母為主元(未知數(shù)),將其他字母看成常數(shù),把代數(shù)式整理成關于“主元”的降冪(或升冪)排列后,再利用提取公因式、公式法、分組分解法等,或多種方法綜合運用進行分解.

三、求代數(shù)式的(最)值

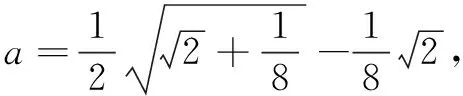
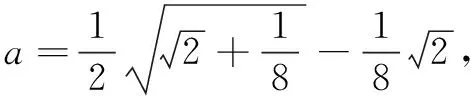
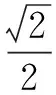
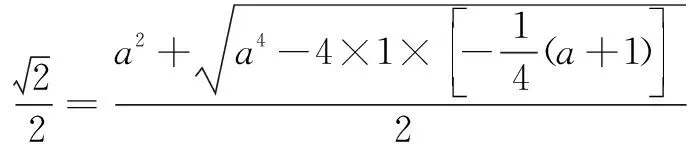
點評該解法巧妙地利用常量與變量的相互轉(zhuǎn)化,并利用一元二次方程的求根公式使問題獲解.

例4(2011年全國初中數(shù)學競賽試題)已知x,y,z為實數(shù)，且滿足x+2y-5z=3,x-2y-z=-5,則x2+y2+z2的最小值是( )

解析對于變量x,y,z，視z為“主元”，這樣將另兩個變量x,y用z的式子分別表示后，代入目標式求解.

∴x2+y2+z2

=(3z-1)2+(z+2)2+z2

=11z2-2z+5

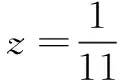
故選D.

點評本題視z為“主元”,先將x,y均用關于z的式子表示，再代入目標式轉(zhuǎn)化為關于“主元”z的二次函數(shù)，最后利用二次函數(shù)的性質(zhì)求解.

四、解方程

例5(第3屆“祖沖之杯”初中數(shù)學邀請賽)求出所有這樣的正整數(shù)a,使得二次方程ax2+2(2a-1)x+4(a-3)=0至少有一個整數(shù)根.

解析將a視為“主元”,則由ax2+2(2a-1)x+4(a-3)=0，得(x2+4x+4)a=2x+12,∴(x+2)2a=2x+12.

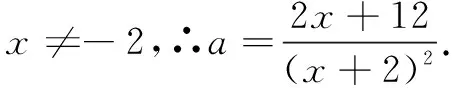
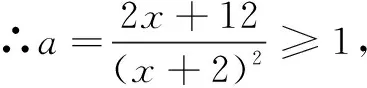
∴2x+12≥(x+2)2,即x2+2x-8≤0，

解得-4≤x≤2,且x≠-2.

又x是整數(shù)根，

∴x只能取-4,-3,-1,0,1,2.

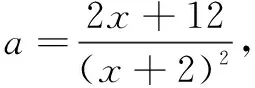
點評本題 “主、次”換位,視正整數(shù)a為“主元”,先分離出a,然后根據(jù)a是正整數(shù),轉(zhuǎn)化為x的不等式求解.

五、確定取值范圍

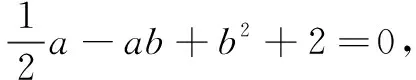
(A)a≤-2

(B)a≥4

(C)a≤-2或a≥4

(D)-2≤a≤4

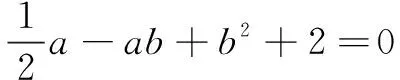
∵b是實數(shù),

即a2-2a-8≥0，

解得a≤-2或a≥4.

故選C.

點評本題視b為“主元”,將已知等式轉(zhuǎn)換為關于“主元”b的一元二次方程,進而利用判別式求解.

例7(第38屆“希望杯”全國邀請賽試題改編)當-1≤a≤1時,不等式x2+(a-4)x+4-2a≥0恒成立,則x的取值范圍是______.

解析視參數(shù)a為“主元”,將原不等式化為(x-2)a+(x2-4x+4)≥0.

令關于a的 “一次”函數(shù)y=(x-2)a+(x2-4x+4),

(1)當x=2時,不等式顯然恒成立;

(2)當x≠2時,由一次函數(shù)圖象的性質(zhì),得當a=-1時,y≥0,且當a=1時,y≥0,

由此得到關于x的不等式組

對于x2-5x+6≥0，解得x≤2，或x≥3;

對于x2-3x+2≥0，解得x≤1,或x≥2.

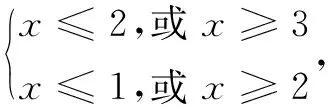
綜合(1)、(2)，x的取值范圍是x≤1,或x=2,或x≥3.

點評在各類考試題中,常出現(xiàn)這樣一類問題:系數(shù)中含有參數(shù)的關于變量x(或x的式子)的一元二次不等式,其參數(shù)在某給定的區(qū)間上且最高次數(shù)為1,求當不等式恒成立時,變量x的取值范圍.此類問題如果直接考慮關于x的一元二次不等式則難以處理.但如果視參數(shù)為 “主元”,將關于x(或x的式子)的“二次”不等式轉(zhuǎn)化為關于參數(shù)的“一次”不等式,再利用一次函數(shù)的性質(zhì),構(gòu)建出一個關于變量x的不等式(組),進而求出x的取值范圍,則是一條簡明而有效的途徑.

六、求解函數(shù)問題

例8(第22屆“希望杯”全國數(shù)學邀請賽初三第一試試題)若對于p的任意值,拋物線y=2x2-px+3p+1都過一個定點,則這個定點的坐標是______.

解析因為定點與“參數(shù)”p無關,所以可視p為“主元”,將二次函數(shù)的解析式化為關于p的一次方程,由各個“系數(shù)”均為0求解.

由y=2x2-px+3p+1變形，得

(-x+3)p+(2x2+1-y)=0.

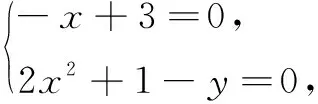
故定點的坐標是(3，19).

點評圖象過定點,即與參數(shù)無關，我們可視參數(shù)為“主元”,將解析式變形整理為含參數(shù)和不含參數(shù)的兩部分,然后令參數(shù)的“系數(shù)”和不含參數(shù)的部分均為0,從而求出定點.

常量與變量不是一成不變的,有時還會相互轉(zhuǎn)化.一個量在一種背景下為變量,而在另一種背景下可以為常量，我們要根據(jù)問題的實際情境認清是常量還是變量.只有這樣才能理解問題實質(zhì),準確有效地解題.“主元法”反映了化歸轉(zhuǎn)化數(shù)學思想在解題中的應用,是數(shù)學思維靈活性的具體表現(xiàn).在解題中,我們要抓住問題的本質(zhì),掙脫“定勢”思維框架的束縛,靈活地利用有效的數(shù)學方法解決問題.